Advances in Pure Mathematics
Vol.06 No.05(2016), Article ID:65362,4 pages
10.4236/apm.2016.65022
Block-Transitive 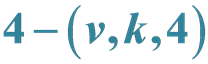 Designs and Ree Groups
Designs and Ree Groups
Shaojun Dai1, Ruihai Zhang2
1Department of Mathematics, Tianjin Polytechnic University, Tianjin, China
2Department of Mathematics, Tianjin University of Science and Technology, Tianjin, China
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).



Received 27 February 2016; accepted 4 April 2016; published 7 April 2016
ABSTRACT
This article is a contribution to the study of the automorphism groups of 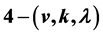 designs. Let
designs. Let 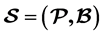 be a non-trivial
be a non-trivial  design where
design where 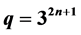 for some positive integer
for some positive integer , and
, and  is block-transitive. If the socle of G is isomorphic to the simple groups of lie type
is block-transitive. If the socle of G is isomorphic to the simple groups of lie type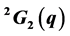 , then G is not flag-transitive.
, then G is not flag-transitive.
Keywords:
Flag-Transitive, Block-Transitive, t-Design, Ree Group

1. Introduction
For positive integers 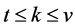 and
and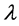 , we define a
, we define a 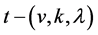 design to be a finite incidence structure
design to be a finite incidence structure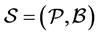 , where
, where 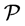 denotes a set of points,
denotes a set of points,  , and
, and 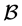 a set of blocks,
a set of blocks, 













For historical reasons, a 


Investigating t-designs for arbitrary
Theorem 1. ( [1] ) Let 







Recently, Huber (see [2] ) completely classified all flag-transitive Steiner t-designs using the classification of the finite 2-transitive permutation groups. Hence the determination of all flag-transitive and block-transitive t-designs with 
The present paper continues the work of classifying block-transitive t-designs. We discuss the block-transitive 
Main Theorem. Let 






The second section describes the definitions and contains several preliminary results about flag-transitivity and t-designs. In 3 Section, we give the proof of the Main Theorem.
2. Preliminary Results
The Ree groups 











Here we gather notation which are used throughout this paper. For a t-design 








Lemma 1. ( [2] ) Let G act flag-transitively on 

1)

2)

3)

Lemma 2. ( [8] ) Let 

Lemma 3. ( [8] ) Let 

1)
2)
Corollary 1. Let 



Proof. By Lemma 2, we have

Hence
We get
3. Proof of the Main Theorem
Suppose that G acts flag-transitively on 












First, we will proof that if 


Suppose that



is transitive on








Sylow 3-subgroup of

So











Now, we can continue to prove our main theorem. Obviously, 

















and




Since G acts flag-transitively on 
Again by Lemma 3(2) and Lemma 1(3),
Thus
By Lemma 2,
Again by Corollary 1,
This is impossible.
This completes the proof the Main Theorem.
Cite this paper
Shaojun Dai,Ruihai Zhang, (2016) Block-Transitive 4-(v,k,4) Designs and Ree Groups. Advances in Pure Mathematics,06,317-320. doi: 10.4236/apm.2016.65022
References
- 1. Cameron, P.J. and Praeger, C.E. (1992) Block-Transitive t-Designs, II: Large t. In: De Clerck, F., et al., Eds., Finite geometry and Combinatorics, Deinze. (1993) London Math. Soc. Lecture Note Series, Vol. 191, Cambridge Univ. Press, Cambridge, 103-119.
- 2. Huber, M. (2009) Flag-Transitive Steiner Designs. Birkhauser Basel, Berlin, Boston.
http://dx.doi.org/10.1007/978-3-0346-0002-6 - 3. Ree, R. (1961) A Family of Simple Groups Associated with the Simple Lie Algebra of Type (G2). American Journal of Mathematics, 83, 432-462.
http://dx.doi.org/10.2307/2372888 - 4. Kleidman, P.B. (1988) The Maximal Subgroups of the Chevally Groups 2G2(q) with q Odd, the Ree Groups 2G2(q), and Their Automorphism Groups. Journal of Algebra, 117, 30-71.
http://dx.doi.org/10.1016/0021-8693(88)90239-6 - 5. Liu, W.J., Zhou, S., Li, H. and Fan, X. (2004) Finite Linear Spaces Admitting a Ree Simple Group. European Journal of Combinatorics, 25, 311-325.
http://dx.doi.org/10.1016/j.ejc.2003.10.001 - 6. Dai, S.J. and Zhang, R.H. (2013) The Designs with Block-Transitive Automorphism. Ars Combinatoria, 110, 15-21.
- 7. Dixon, J.D. and Mortimer, B. (1996) Permutation Groups. Springer Verlag, Berlin.
http://dx.doi.org/10.1007/978-1-4612-0731-3 - 8. Shen, H. (1990) The Theory of Combinatorial Design. Shanghai Jiaotong Univ. Press, Shanghai.













