Received 9 December 2015; accepted 26 March 2016; published 29 March 2016

ABSTRACT

Here, we determine formulae, for the numbers of representations of a positive integer by certain sextenary quadratic forms whose coefficients are 1, 2, 3 and 6.

Keywords:

Sextenary Quadratic Forms, Representations, Theta Functions, Dedekind Eta Function, Eisenstein Series, Eisenstein Forms, Modular Forms, Cusp Forms

1. Introduction

The divisor function 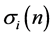is defined for a positive integer i by

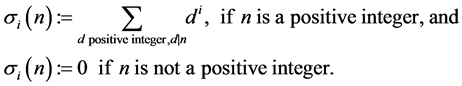
The Dedekind eta function and the theta function are defined by

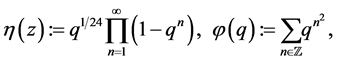
where

and an eta quotient of level N is defined by

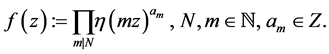(1)

It is important and interesting to determine explicit formulas of the representation number of positive definite quadratic forms.

Here we give the following Lemma, see ( [1] , Theorem 1.64), about the modularity of an eta quotient.

Lemma 1. An eta quotient of level N is a meromorphic modular form of weight 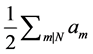on 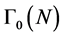having rational coefficients with respect to q if

a)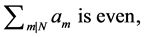

b)

c)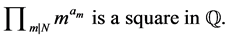

For 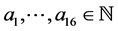and a nonnegative integer n, we define

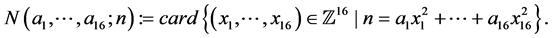
Clearly 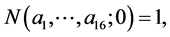and without loss of generality we can assume that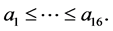

Now, let’s consider sextenary quadratic forms of the form

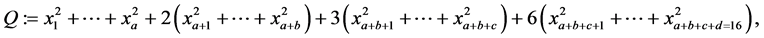
where,

We write to denote the number of representations of n by a sextenary quadratic form. Its theta function is obviously

Formulae for for the nine octonary quadratic forms (2i, 2j, 2k, 2l) = (8, 0, 0, 0), (2, 6, 0, 0), (4, 4, 0, 0), (6, 2, 0, 0), (2, 0, 6, 0), (4, 0, 4, 0), (6, 0, 2, 0), (4, 0, 0, 4), and (0, 4, 4, 0) appear in the literature, (cf. [2] - [12] ). Alaca and Williams have obtained some results on sextenary quadratic forms in terms of the functions and, see [13] [14] . There are more works on representation number of sextenary quadratic forms in [15] - [17] . Other methods for representation number have been used in (cf. [7] [10] [12] [18] [19] ). Here, we will classify all fourtuples for which is a modular form of weight 8 with level 24. Then we will obtain their representation numbers in terms of the coefficients of Eisenstein series and some eta quotients.

First, by the following Theorem, we characterize the facts that

are in

Theorem 1. Let

where, , be a sextenary quadratic form. Then its theta series is of the form

Moreover, it is in if and only if is given in the Table 1. Here we also see that are either both even or both odd.

Proof. It follows from the Lemma 1, holomorphicity criterion in ( [20] Corollary 2.3, p. 37) and the fact

that

The condition is a square of a rational number implies that either are both even or both odd integers.

Now let,

the unique newform in

Theorem 2. The set

is a basis of. Moreover, the unique newform in is, the unique newform in is, the two unique newforms in are

the two unique newforms in are

and the three unique newforms in are

Proof. is 32 dimensional, is 24 dimensional, see ( [21] Chapter 3, p. 87 and Chapter 5, p. 197), and generated by

where is the unique newform in; is the unique newform in; is the unique newform in, are the unique newforms in; are the unique newforms in and are the unique newforms in.

As a consequence of this Theorem, we have obtained the following Corollary.We have used Magma for the calculations.

2. Corollary

The following representation numbers formulae are valid.

Cite this paper

Barış Kendirli, (2016) Representations by Certain Sextenary Quadratic Forms Whose Coefficients Are 1, 2, 3 and 6. Advances in Pure Mathematics,06,212-296. doi: 10.4236/apm.2016.64018

References