Received 11 November 2015; accepted 8 December 2015; published 11 December 2015

ABSTRACT

In this article, a class of Dirichlet problem with L^p boundary data for polyharmonic function in the upper half plane is mainly investigated. By introducing a sequence of kernel functions called higher order Poisson kernels and a hierarchy of integral operators called higher order Pompeiu operators, we obtain a main result on integral representation solution as well as the uniqueness of the polyharmonic Dirichlet problem under a certain estimate.

Keywords:

Dirichlet Problem, Polyharmonic Function, Higher Order Poisson Kernels, Higher Order Pompeiu Operators, Non-Tangential Maximal Function, Uniqueness

1. Introduction

Usually harmonic functions are defined by Laplace operator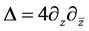, where 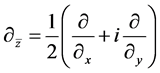is the Cauchy-Riemann operator and 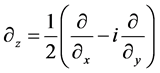is the adjoint operator of C-R operator. By iterating the

Laplace operator, one can define the so-called polyharmonic functions by [1] . In [2] , Goursat obtained his decomposition formula, in [3] , Vekua developed one method to construct an approximative solution of the biharmonic Dirichlet problem in a simply connected domain. In recent years, the study of explicit solution of BVPS (boundary value problems) has undergone a new phase of development [4] - [6] . There are Dirichlet, Neumann and Robin boundary value problems in regular domain (in the disc [4] ; and in the upper half plane [5] ) and in irregular domains (Lipschitz domains [6] ). Although, there are many marked works about the BVPS, few of them give a certain estimate about the uniqueness of the solution. Thus, the purpose of this article is devoted to solving the unique solution of the following polyharmonic Dirichlet problems (for short, PHD) for 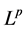data in the upper half plane, H, i.e.

(1.1)

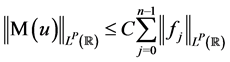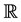with, where is the Laplacian, and is the real axis, for some

suitable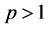, , 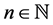, 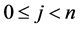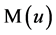is the non-tangential maximal function of u, which is defined by

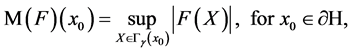
where is the non-tangential approach region, viz.,

where.

It is clear that all the boundary data in BVPs (1.1) are non-tangential.

2. Preliminary and Some Lemmas

Definition 2.1. If a real valued function satisfies the equation, in D, then f is called an n-harmonic function in D, concisely, a polyharmonic function.

We use the notation denoting the set of polyharmonic function of order n in D. Especially, is the set of all harmonic functions in D.

Lemma 2.2. [7] Let D be a simply connected (bounded or unbounded) domain in the complex plane with smooth boundary. If, then for any, there exist functions, such that

(2.1)

where denotes the real part. The above decomposition expression of f is unique in the sense of the equi- valence relation, more precisely, for.

Corollary 2.3. If the sequence of functions defined in D satisfy

(1);

(2) in D for.

Then for, and

(2.2)

where is the analytic jth decomposition component of the n-harmonic function. It must be noted that (2.2) holds in the sense of the equivalence relation.

Definition 2.4. A sequence of real-valued functions of two variables defined on is called a sequence of higher order Poisson kernels, more precisely, is called the nth order Poisson kernel, if they satisfy the following conditions.

(1) For all; with any fixed; and, with any fixed, and the non-tangential boundary value

exists for all t and; can be continuously extended to for any fixed;

(2) and and, and for any

uniformly on whenever, where is any compact set in, M, T are positive constants depending only on and n;

(3) and for;

(4), a.e., for any;

(5), for any,

where all limits are non-tangential.

Definition 2.5. Let D be a simply connected (bounded or unbounded) domain in the plane with smooth boundary, and denote the set of all analytic functions in D. If f is a continuous function defined on satisfying for any fixed, and, , for any fixed, then f is called on and this is noted by.

Lemma 2.6. [8] If is a sequence of higher order Poisson kernels defined on, i.e.,

fulfills the aforementioned properties 1 - 5 in Definition 2.4, then, for, there exist functions

defined on such that

(2.3)

with

(2.4)

for

(2.5)

for with respect to and

(2.6)

Moreover,

(2.7)

is the classical Poisson kernel for the upper half plane. All of the above, the non- tangential boundary value

(2.8)

exists on, except and for any fixed. We can further show that

can be continuously extended to for any fixed, and

(2.9)

uniformly on whenever which is any compact set in, where M, T are positive constants depending only on.

Moreover,

(2.10)

for any and.

Remark 2.7. Lemma 2.6 provides a algorithm to obtain all explicit expressions of higher order Poisson kernels appeared in [8] .

3. Homogeneous PHD Problem in the Upper Half Plane

In order to solve the homogeneous PHD problems (1.1) and get the uniqueness of its solution, we need the following lemmas.

Lemma 3.1. [8] Let D be a simply connected unbounded domain in the plane with smooth boundless boundary. If and there exists, such that

(3.1)

uniformly on whenever which is any compact set in D, where M, T, are positive constants depending only on. Then

.

Lemma 3.2. [8] Let be the sequence of higher order Poisson kernels defined on, then

for any and,

. (3.3)

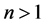
Lemma 3.3. [9] Let, , and be the Poisson integral of f (in our notations,

,), then

(3.4)

where is the cone in with the vertex at and the aperture, ,; is a positive constant depending only on, is the non-tangential maximal function, and is the standard Hardy-Littlewood maximal function defined by

(3.5)

Lemma 3.4. (Hardy-Littlewood maximal theorem, see [10] ) Let, , then is finite almost everywhere on. Moreover,

(1) If, then is in, more precisely

(3.6)

(2) If, , then

(3.7)

where is a constant depending only on p.

Corollary 3.5. for any with, where is a constant depending only on. Moreover,

(3.8)

for any, and for any, , is finite almost everywhere on, is a positive constant depending only on.

Theorem 1. Let be the sequence of higher order Poisson kernels defined on, then for any,

(3.9)

is the unique solution of PHD problem (1.1)

Proof. Since the higher order Poisson kernels possess the inductive property as stated in Definition 2.4. Act on the two sides of (3.9) with the polyharmonic operator,. We have

(3.10)

since the Laplace operator is. Thus, for on,

(3.11)

follow from Lemma 2.6 and the nice property of G, i.e.,

(3.12)

for any.

Similarly, letting the polyharmonic operator act on the two sides of (3.9), we have for any. Thus (3.9) is a solution of the PHD problem (1.1).

Next we turn to the estimate and uniqueness of the solution. By Definition 2.4 and Corollary 3.5, we have

As discussed above, the uniqueness of solution follows.

4. Inhomogeneous PHD Problem in the Upper Plane

Due to the limited knowledge of the author, at this section, we only consider the bounded domain D for in- homogeneous PHD problem in the upper half-plane, i.e.

(4.1)

where, such that, for some, , as and for some suitable. In order to solve the inhomogeneous PHD problem (4.1), we need the higher order Pompeiu operators which are higher order analogues of the classical Pompeiu operators.

Definition 4.1. [11] Let kernels

(4.2)

where m and n are integer, with but. Then, we formally define operators, acting on suitable complex valued function w defined in D, a domain in the plane, according to

(4.3)

The following properties of are needed in the sequel. They are partial results from [11] .

Lemma 4.2. Assume, and let w be a complex valued function in such that for some,

Then, the integral converges absolutely for almost all z in and, provides that p satisfies con- ditions,

.

Proof. See Corollary 4.6 in [11] .

Lemma 4.3. Assume, and let w be a measurazble complex valued function in such that for some,

(4.4)

(a) If and, then in the sense of Sobolev derivatives in the entire plane,

(4.5)

(4.6)

(b) If and for some, then (4.5) and (4.6) again hold in the sense of Sobolev derivatives in; moreover, the formulas

(4.7)

are valid in even in the case of.

Proof. See Corollary 5.4 in [11] .

Theorem 2. The problem of (4.1) is solvable and its unique solution is

(4.8)

where and are the higher order Pompeiu operators, and are the former n higher order Poisson kernel functions.

Proof. Through Lemma 4.2 and Lemma 4.3, we get

(4.9)

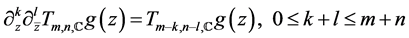
in the Sobolev sense. Moreover,

. (4.10)

Noting (4.9) we know that is a week solution of the inhomogeneous equation

and for some

(4.11)

By the aforementioned, the problem (4.1) is equivalent to the PHD problem of simplified form

So, through Theorem 1 as well as the estimate of the solution, we complete the proof of Theorem 2.

Cite this paper

Kanda Pan, (2015) L^p Polyharmonic Dirichlet Problems in the Upper Half Plane. Advances in Pure Mathematics,05,828-834. doi: 10.4236/apm.2015.514077

References