Received 6 July 2015; accepted 8 November 2015; published 11 November 2015

ABSTRACT

For the cube root of a positive integer, a direct method to determine the floor of integer combination of the cube root and its square is given.

Keywords:

Cube Root, Integer Part, Continued Fraction

1. Introduction

The continued fraction expansion of 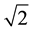can be calculated as follow(cf. [1] -[3] ).

Because

hence

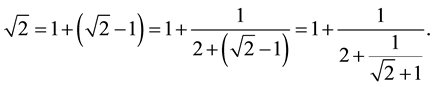
When one calculates the continued fraction expansion of it is important to determine the integer part of 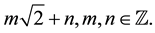For square root, its continued fraction expansion can be obtained easily because it is circled while there is no obvious method to do so for cube root. In this note, we will determine the integer part of cube root and its combination. So we can achieve the continued fraction expansion of cube root according to the integer part of the cube root.

2. Main Results

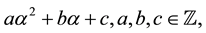Let N be a positive integer and not a cube. Denote as its cube root. For set

Then these numbers are satisfied the identity:

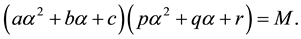(1)

We achieve two interesting properties on 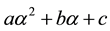and.

Theorem 1. If, then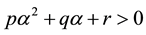. Therefore the number 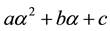has the same sign as M.

We consider two cases respectively.

1) If.

a) If. Substituting into the expression, then we have

since every term in the last expression is nonnegative.

b) If. We have also the similar expression as case a):

The above inequality holds because

2) If

a) If Then we have

We also have

Hence by the identity (1)

b) If Then Because of therefore

So we show that for both cases. According to identity (1), both and M have the same sign.

Remark 1. The result is very amazing. Because the quotient ring is a filed, where is the maximal ideal generated by the irreducible polynomial. For any there exists such that

But it is surprising that the number defined in Theorem 1 is always positive.

Theorem 2. If and then

That is to say, is the biggest integer less than or equal to

According to Theorem 1,

Hence

So

The proof is completed.

Remark 2. Applying the Theorem 2, we can design an algorithm to calculate the continued fraction expansion of the cube root.

Acknowledgements

The authors wish to thank Prof. Xiangqin Meng for her some helpful advices.

Cite this paper

ZhongguoZhou, (2015) Integer Part of Cube Root and Its Combination. Advances in Pure Mathematics,05,774-776. doi: 10.4236/apm.2015.513071

References