Advances in Pure Mathematics
Vol.05 No.06(2015), Article ID:56188,14 pages
10.4236/apm.2015.56033
The Distribution of Prime Numbers and Finding the Factor of Composite Numbers without Searching
Dagnachew Jenber
School of Interdisciplinary Program, Mathematics Division, Addis Ababa Science and Technology University, Addis Ababa, Ethiopia
Email: djdm_101979@yahoo.com
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 26 March 2015; accepted 2 May 2015; published 8 May 2015
ABSTRACT
In this paper, there are 5 sections of tables represented by 5 linear sequence functions. There are two one-variable sequence functions that they are able to represent all prime numbers. The first one helps the last one to produce another three two-variable linear sequence functions. With the help of these three two-variable sequence functions, the last one, one-variable sequence function, is able to set apart all prime numbers from composite numbers. The formula shows that there are infinitely many prime numbers by applying limit to infinity. The three two-variable sequence functions help us to find the factor of all composite numbers.
Keywords:
The nth Sequence of an Arithmetic Sequence, Number of Elements of the Set, Sequence Functions

1. Introduction
A prime number (or a prime) is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example, 5 is prime because 1 and 5 are its only positive integer factors, whereas 6 is composite because it has the divisors 2 and 3 in addition to 1 and 6. The fundamental theorem of arithmetic establishes the central role of primes in number theory: any integer greater than 1 can be expressed as a product of primes that is unique up to ordering. The uniqueness in this theorem requires excluding 1 as a prime because one can include arbitrarily many instances of 1 in any factorization, e.g., 3, 1 × 3, 1 × 1 × 3, etc. are all valid factorizations of 3. The property of being prime (or not) is called primality. A simple but slow method of verifying the primality of a given number n is known as trial division. It consists of testing whether n is a multiple of any integer between 2 and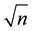 . Algorithms much more efficient than trial division have been devised to test the primality of large numbers. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of April 2014, the largest known prime number has 17,425,170 decimal digits. There are infinitely many primes, as demonstrated by Euclid around 300 BC. There is no known useful formula that sets apart all of the prime numbers from composites. However, the distribution of primes, that is to say, the statistical behaviour of primes in the large, can be modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability that a given, randomly chosen number n is prime is inversely proportional to its number of digits, or to the logarithm of n. Many questions regarding prime numbers remain open, such as Goldbach’s conjecture (that every even integer greater than 2 can be expressed as the sum of two primes), and the twin prime conjecture (that there are infinitely many pairs of primes whose difference is 2). Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which makes use of properties such as the difficulty of factoring large numbers into their prime factors. Prime numbers give rise to various generalizations in other mathematical domains, mainly algebra, such as prime elements and prime ideals [1] .
. Algorithms much more efficient than trial division have been devised to test the primality of large numbers. Particularly fast methods are available for numbers of special forms, such as Mersenne numbers. As of April 2014, the largest known prime number has 17,425,170 decimal digits. There are infinitely many primes, as demonstrated by Euclid around 300 BC. There is no known useful formula that sets apart all of the prime numbers from composites. However, the distribution of primes, that is to say, the statistical behaviour of primes in the large, can be modelled. The first result in that direction is the prime number theorem, proven at the end of the 19th century, which says that the probability that a given, randomly chosen number n is prime is inversely proportional to its number of digits, or to the logarithm of n. Many questions regarding prime numbers remain open, such as Goldbach’s conjecture (that every even integer greater than 2 can be expressed as the sum of two primes), and the twin prime conjecture (that there are infinitely many pairs of primes whose difference is 2). Such questions spurred the development of various branches of number theory, focusing on analytic or algebraic aspects of numbers. Primes are used in several routines in information technology, such as public-key cryptography, which makes use of properties such as the difficulty of factoring large numbers into their prime factors. Prime numbers give rise to various generalizations in other mathematical domains, mainly algebra, such as prime elements and prime ideals [1] .
In this paper I am going to prove that:
1) 1 is prime number, so the definition of prime number becomes “A prime number (or a prime) is a natural number greater than or equal to 1 that has no positive divisors other than 1 and itself.”
2) There is useful formula that sets apart all of the prime numbers from composites or the distribution of primes.
3) Goldbach’s conjecture and the twin prime conjecture.
4) Finding the factor of any odd composite numbers without searching.
For example to find the factor of composite number
n = 114381625757888867669235779976146612010218296721242362562561842935706935245733897830597 123563958705058989075147599290026879543541 [2] the only thing we need to have is microsoft Excel soft-
ware with big cell and a little bit big screen computer and track the number 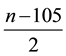 from the two tables using
from the two tables using
two functions that we will discuss. My paper is important to find the factor composite numbers and prime numbers as we want as fast as possible and faster than trial division and algorithmic methods and perfect.
2. Preliminary
Definition (When Is a Number Divisible by 3) [3] .
If the sum of the digits of a number is divisible by 3 , then the original number is divisible by 3.
Definition (When Is a Number Divisible by 5) [3] .
If the last digit of the number being inspected for divisibility is either a 0 or 5, then the number itself will be divisible by 5.
Definition (When Is a Number Divisible by 7) [3] .
Delete the last digit from the given number and then subtract twice this deleted digit from the remaining number. If the result is divisible by 7, the original number is divisible by 7. This process may be repeated if the result is too large for simple inspection of divisibility of 7.
Definition (The 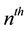 term of Arithmetic sequence).
term of Arithmetic sequence).
The 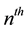 term of an Arithmetic sequence is given by
term of an Arithmetic sequence is given by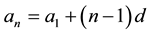 , where
, where 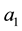 is the first term of the sequence and d is the common difference of the sequence.
is the first term of the sequence and d is the common difference of the sequence.
Definition (Multivariable sequence function).
A function  is a real valued multi-variable sequence function defined on the set of
is a real valued multi-variable sequence function defined on the set of  natural numbers,
natural numbers,  , where
, where 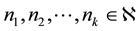 and number of elements in the range
and number of elements in the range
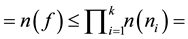 the product of number of elements of
the product of number of elements of 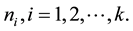
Example: If  for
for
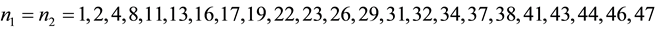 , that is,
, that is,  , then
, then
number of elements of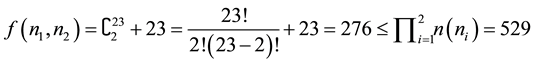 , here I take combination
, here I take combination
because addition is commutative from 

But if

traction is not commutative from 

3. Tables
Theorem 1. The linear sequence function 


Proof. The sequence function 

Theorem 2. The linear sequence function 
Proof. The function 

Theorem 3. The linear sequence function 

Proof. Since


Theorem 4. The linear sequence function 


Proof. See Table 1. □
Table 1. My magical table.
Theorem 5. The sequence function 


Proof. From combination of objects 



Thus 
Theorem 6. If





Proof. Since 



Theorem 7. The sequence function 



Proof. Since

See the following table, where 



Example: For Theorem 7 see the following Table 2, Table 3 which represents 



Table 2. Tabular proof for theorem 7.
Table 3. Tabular proof for theorem 7 continued.
Theorem 8. If the sequence function, 






Proof. Since





Theorem 9. If the sequence function, 









Proof. If 


Thus 




Example: For Theorem 9 see the following Table 4, Table 5 which represents 



Table 4. Examples for theorem 9.
Table 5. Examples for theorem 9 continued.
Theorem 10. If the sequence function, 





Proof. Since 




Theorem 11. If the sequence function, 








Proof. If 


Thus 




Example: For Theorem 11 see the following Tables 6-8 which represents 



Table 6. Examples for theorem 11.
Table 7. Examples for Theorem 11 continued.
Table 8. Examples for Theorem 11 continued.
Theorem 12. The union of three sequence functions, 





Proof. Let 









Therefore
Theorem 13. If 









Proof. Since 
or 
or 



Theorem 14. The sequence function, 









Proof. Suppose 

But 





Therefore, there exists a number 

Theorem 15. There are infinitely many prime numbers.
Proof. Since
Theorem 16. (Goldbach’s theorem)
Every even integer greater than or equal to 2 can be expressed as the sum of two primes.
Proof. Suppose 










Thus for all 








Or for all 











Or for all 









Therefore from Equations (1), (2), and (3) we have





Thus every even integer greater than or equal to 2 can be expressed as the sum of two primes. □
Theorem 17. (Twin prime theorem)
There are infinitely many pairs of primes whose difference is 2.
Proof. Suppose there are infinitely many numbers










Thus 



Theorem 18. Suppose










and 

If










Proof. Since 



Now let 




































Thus we have to eliminate 

Therefore we have 

Since we have 24 number of prime numbers less than 107, hence



Example: For Theorem 12 - 18 see the following Tables 9-16. Where the bold face numbers are elements of 








Table 9. Examples for theorem 12 - 18.
Table 10. Examples for theorem 12 - 18 continued.
Table 11. Examples for theorem 12 - 18 continued.
Table 12. Examples for theorem 12 - 18 continued.
Table 13. Examples for theorem 12 - 18 continued.
Table 14. Examples for theorem 12 - 18 continued.
Table 15. Examples for theorem 12 - 18 continued.
Table 16. Examples for theorem 12 - 18 continued.
Acknowledgements
I thank the editors and the referee for their comments and thanks to my brothers, colleagues and friends: Adem Gulma, Dereje Wasihun, Natnael Nigussie, Ketsela Hailu, Yadeta Chimdessa, Solomon Tesfaye and Abebe Tamrat for thier encouragement and advice next to God and my family.
References
- (2015) http://en.wikipedia.org/wiki/Prime_number
- Posametier, A.S. (2003) Math Wonders to inspire Teachers and Students.
- Crandall, R. and Pomerance, C.B. (2005) Prime numbers: A Computational Perspective. 21.











