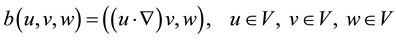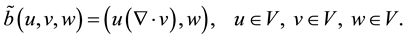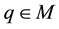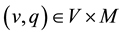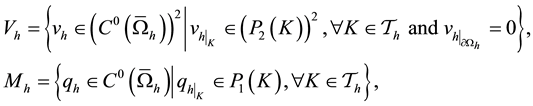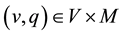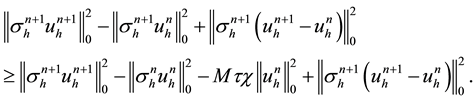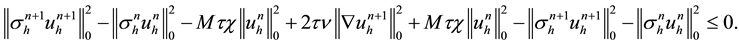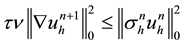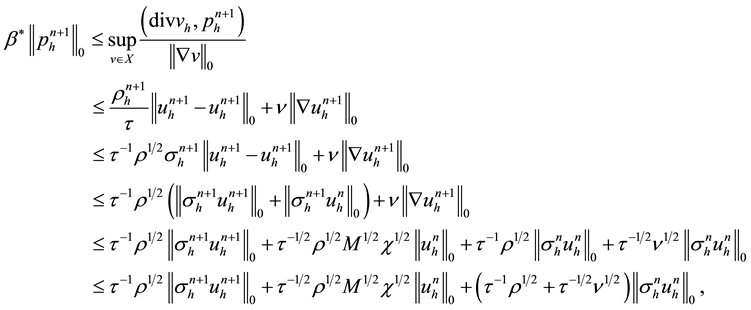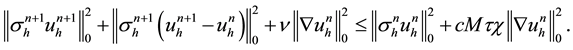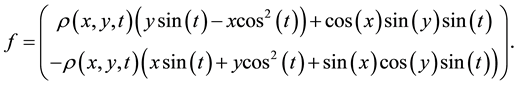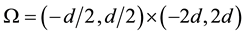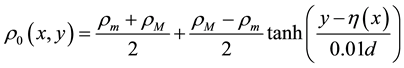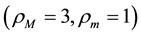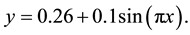Advances in Pure Mathematics
Vol.05 No.05(2015), Article ID:55541,15 pages
10.4236/apm.2015.55026
A Characteristics-Mix Stabilized Finite Element Method for Variable Density Incompressible Navier-Stokes Equations
Fei Xiong1, Liquan Mei2, Ying Li3, Wu Zhang3
1Kunming Medical University Haiyuan College, Kunming, China
2School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an, China
3School of Computer Engineering and Science, Shanghai University, Shanghai, China
Email: feimeng2000cn@aliyun.com, lqmei@mail.xjtu.edu.cn, leeying840223@163.com, wzhang@shu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 March 2015; accepted 7 April 2015; published 13 April 2015
ABSTRACT
This paper describes a characteristics-mix finite element method for the computation of incompressible Navier-Stokes equations with variable density. We have introduced a mixed scheme which combines a characteristics finite element scheme for treating the mass conservation equation and a finite element method to deal with the momentum equation and the divergence free constraint. The proposed method has a lot of attractive computational properties: parameter-free, very flexible, and averting the difficulties caused by the original equations. The stability of the method is proved. Finally, several numerical experiments are given to show that this method is efficient for variable density incompressible flows problem.
Keywords:
Characteristic Finite Element, Variable Density Flows, Naiver-Stokes Equations, Stabilized Method

1. Introduction
This paper is devoted to the numerical approximation of incompressible viscous flows with variable density. This type of flows is governed by the time-dependent Navier-Stokes equations [1] [2] :
 (1)
(1)
where the dependent variables are the density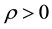 , the velocity field
, the velocity field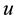 , and the pressure
, and the pressure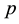 . The constant
. The constant 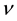 is the dynamic viscosity coefficient and
is the dynamic viscosity coefficient and 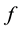 is a driving external force. In stratified flows we typically have
is a driving external force. In stratified flows we typically have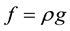 , where
, where 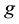 is the gravity field. The fluid occupies a bounded domain
is the gravity field. The fluid occupies a bounded domain 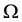 in
in  (with
(with 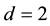 or 3) and a solution to the above problem is sought over a time interval
or 3) and a solution to the above problem is sought over a time interval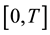 . The Navier-Stokes system is supplemented by the following initial and boundary conditions for
. The Navier-Stokes system is supplemented by the following initial and boundary conditions for  and
and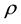 :
:
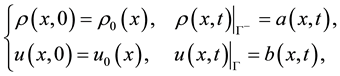 (2)
(2)
where 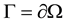 and
and 

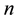
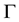


Compared with the constant density incompressible Navier-Stokes equation, the main difficulty for the simu- lation of the system Equation (1)-(2) is that these equations entangle hyperbolic, parabolic, and elliptic features. Therefore, how to construct stable and efficient numerical schemes for the system Equations (1) and (2) is challenging.
For developing numerical approximations to this problem, it seems natural to use, as far as possible, the techniques established for the solution of constant density incompressible Navier-Stokes equations, viz., the fractional step projection method of Chorin [4] [5] and Temam [6] [7] . The method uses a time splitting, solving separately the transport equation for the density and the momentum for the velocity, the incompressible con- straint being treated through a projection method, see [8] . This is the methodology followed in [3] [9] - [11] . Several algorithms have been developed which extend this idea to the situation that concerns us here, see for example [1] - [3] [12] - [14] . Caterina introduces an hybrid scheme which combines a finite volume approach for treating the mass conservation equation and a finite element method to deal with the momentum equation and the divergence free constraint [15] . However, we note also that there is a difficulty which arises with the trans- port equation during the process of calculation. Because the transport equation has the hyperbolic nature, it is not well adapted to a mere treatment by FE methods, but instead requires a specific approach, like Discon- tinuous Galerkin methods, artificial viscosity, sub-grid stabilization procedure as in [3] , see also [16] , or the least-square method as used in [17] . Becase the characteristic methods have proved their efficiency for this kind of problems, such as convection-dominated problems [18] - [21] , a characteristic stabilized finite element scheme is used to deal with the transport equation in this paper. The idea of characteristic methods is to recast the governing equations in terms of the Lagrangian coordinates defined by the particle trajectories (or characteristics) associated with the problem under consideration. The Lagrangian treatment in these methods greatly reduces the time truncation error in Eulerian method [19] . In addition, the characteristic methods have been shown to possess remarkable stability properties.
In this paper, we consider the conserved form for variable density incompressible flows which is introduced by Guermond et al. [1] [3] . Because in the formulation, the mass conservation and momentum equations are rewritten in a new form that guarantees some control on the 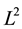
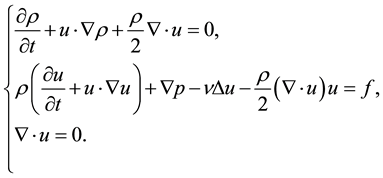
In the above equations Equation (3), the additional term 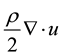

zero if
The originality of our work is to use different numerical methods for the transport equation and for evaluating the evolution of the velocity driven by the last two equations in the system Equation (1). To be more specific, we use a time-splitting, solving the first equation for a given velocity by using a characteristic stabilized finite element approach which is efficient when dealing with a pure convection equation, and then, we compute the divergence free solution of the last two equations by exploiting the advantages of FE methods, see [22] - [24] . Here, we care to preserve the divergence free constraint between the two steps of the splitting. The results show that the proposed algorithm is stable and efficient.
The paper is organized as follows. In next section, we introduce some notations for this paper. In Section 3, a detailed presentation of the new method is given. In Section 4, the stability of the method is proved. In Section 5, a series of numerical experiments are given. The last section is devoted to concluding remarks.
2. Notation
In this section, we aim to describe some of the notations which will be frequently used in this paper. We con- sider the time-dependent variable density Navier-Stokes system Equations (1) and (2) on the finite time interval 
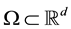
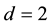


Let 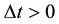
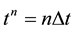
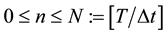
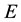

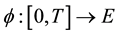
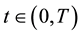
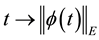


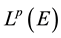


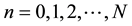
No notational distinction is done between scalar or vector-valued functions but spaces of vector-valued functions are identified with bold fonts. The space of functions in 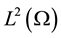



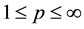
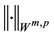
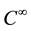
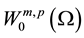
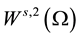
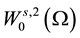
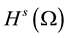
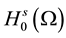
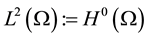
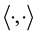
For the mathematical setting of problem Equation (1), we introduce the following Hilbert spaces:

The spaces 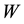





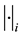


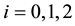
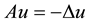
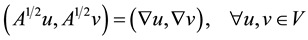
We also introduce the following bilinear operator: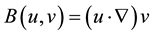

and a trilinear form on 
Obviously, the bilinear 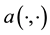
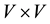

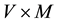
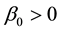
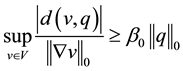
where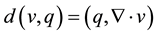
Henceforth 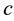
3. Description of the Numerical Scheme
3.1. The Time Splitting Method
Set

Step 1. Solve new density field:
Find 
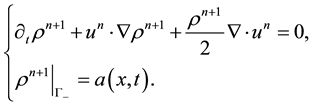
Step 2. Solve new velocity and pressure fields:
Find 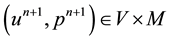

3.2. Solving the Density Equation by a Characteristics Finite Element Scheme
The origin of our scheme can be seen by considering the first equation in a space-time framework. First, for density field
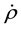
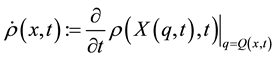
where 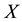
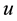
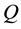
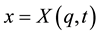
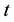
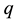
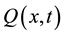

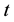
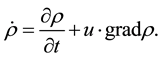
Let us introduce the characteristic curves, which are simply the the trajectories of the motion associated with the velocity field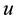
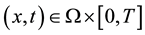
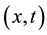
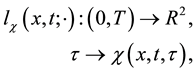
which can be obtained by solving the initial value problem
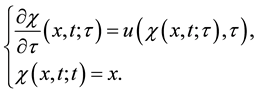
It represents the trajectory described by a material point that is placed at position 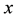
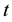

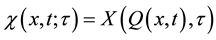
By using function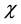
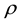


For the time variable, the solution will be approximated at times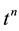
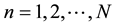

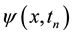
In order to discretize the material time derivative in Equation (5), we use the following first order backward Euler formula, namely,

Moreover, for 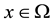
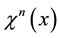

So, let us introduce the following characteristics scheme for time semidiscretization of problem Equation (5)
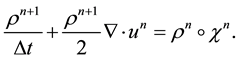
Now, multiplying Equation (14) by a test function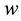
Find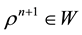

We define finite element space 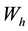
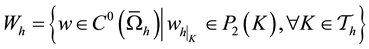
where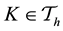
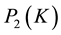
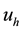
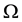
Find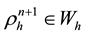
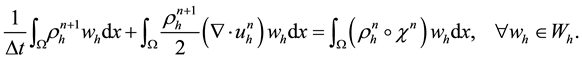
3.3. Solving the Velocity Equation by a FE Method
In the numerical simulation of the Navier-Stokes Equation (6), a major difficulty is that the velocity and the pressure are coupled by the incompressibility constraint. Many researchers have done a lot of work about Navier- Stokes system with constant density, for example [30] -[33] . Here, we can try to use these methods to the varia- ble density Navier-Stokes equation.
Since we aim at using a FE method, it is convenient to write the variational formulation of Equation (6). Let 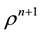

Find 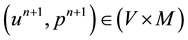

The domain 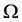

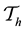
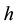
FE spaces 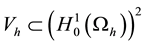
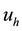
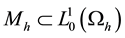
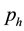
of spaces 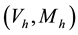
where for all
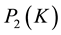

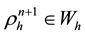
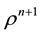

Find 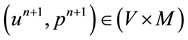

In the next section, we will prove that the above algorithm is stable.
4. Stability Analysis of the Method
In this section, we recalls some useful Propositions and stability hypothesis assumptions for the characteristics- mix finite element method for the incompressible flow with variational density [34] . The approximation method is used to approximate the mass conservation returns 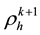
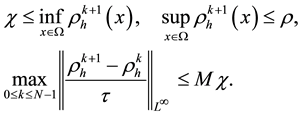
Moreover, we also need the following results [34] to prove the stability of the discrete method presented.
Propositon 4.1. For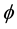
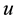




Next, we start with the stability proof of the system. To avoid irrelevant technicalities, we assume that there is no external driving force, i.e.,
Lemma 4.2. Let 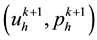

where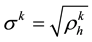
Proof: Taking 
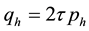
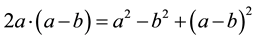

Using (4.1), implies that

Substituting above inequality into (4.4) and using (4.1), yields
So, we have

Similarly,

Substituting above inequality into (4.4) again, leads to
So, we have
which together with (4.6), we can easily obtain the following result
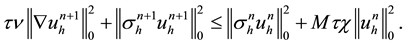
Next, set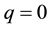
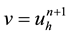
and using the (4.8), a simple derivation leads to
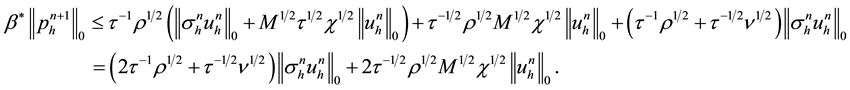
Finally, we obtain the desired stability result.
Theorem 4.3. Let 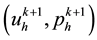
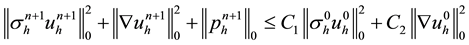
where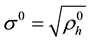
Proof: Taking 

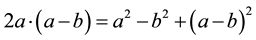
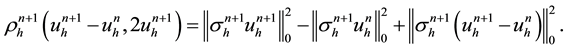
Using (4.1), implies that
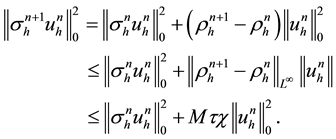
Substituting the above inequality into (4.11) and using (4.1), yields
So, we have

Then using the Poincare inequality, we obtain
Therefore, we can easily get
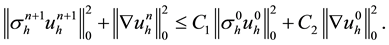
Next, using the above inequality and Poincare inequality again, we have
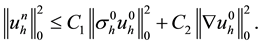
Also, combining (4.14), (4.15) with (4.9), we obtain the desired stability result.
5. Numerical Simulations
In this section, we present four series of numerical results to illustrate the theoretical analysis of the algorithm proposed in this paper.
5.1. Rates of Convergence Study
In order to test the accuracy of the algorithm proposed in this paper, we consider a problem with a known analy- tical solution. We solve the variable density Navier-Stokes equations Equations (1) and (2) in the unit square 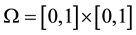
so that the right-hand side to the momentum equation is
We use the 
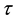
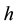
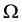
First, we solve the above mentioned problem for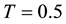
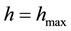

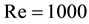
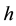
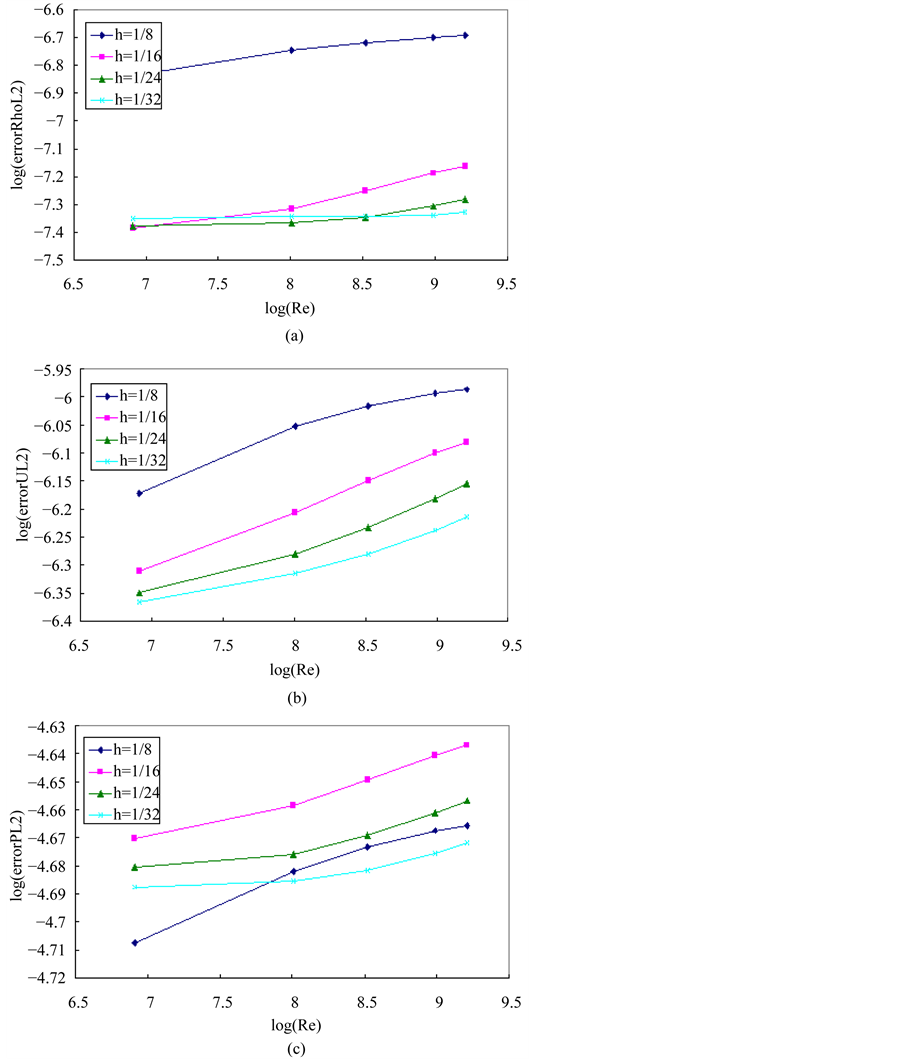
Secondly, computation are made on a fixed mesh size for different Reynolds number (Re = 1000, 3000, 5000,
8000, 10000). Taking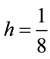
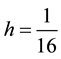
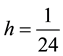
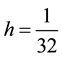
we can see that the stability still keeps well when the Reynolds number increases. These demonstrate that our method is very effective for high Reynolds number.
Next, computation are made on a fixed mesh size and a fixed Reynolds number with different time steps. The computation has been performed for
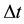
5.2. Rayleigh-Taylor Instability
In this Subsection we illustrate the performance of the method on a realistic problem, namely we investigate a Rayleigh-Taylor instability. The problem has been considered in [1] [3] [15] starting from the results and com- ments in [35] . We compute the development of a Rayleigh-Taylor instability in the viscous regime as docu- mented in [35] - [38] . This problem consists of two layers of fluid initially at rest in the gravity field. It occupies the domain
Table 1. Rates of convergence and error with different mesh size.
Table 2. Rates of convergence and error in time.
Figure 1. Effect of varying h at different Reynolds number. (a) L2 error for the density; (b) L2 error for the velocity; (c) L2 error for the pressure.
which splits into two region with varying density, the heavier fluid superposed to the light one. The interface is slightly smoothed since we set at time
with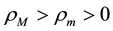

1) the density ratio between the light and the heavy fluid, which is measured by the so-called Atwood number

2) the Reynolds number, defined as
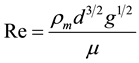
where 



The equations are made dimensionless by using the following references: 
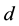
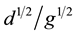

Next, we compare the solutions obtained at different Atwood numbers.
・ A low Atwood number problem: Setting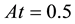

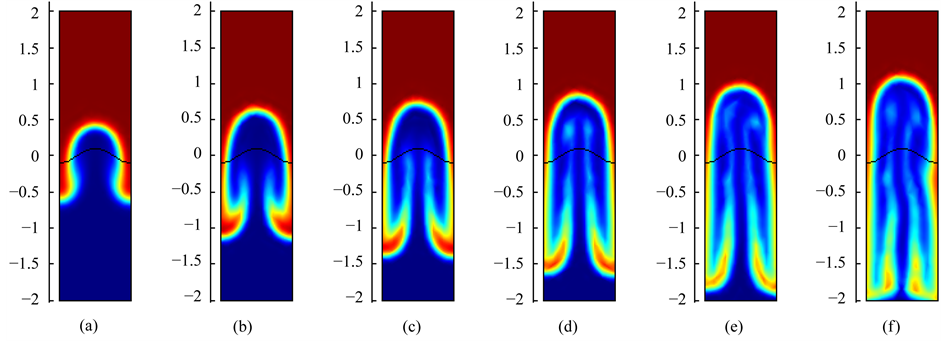
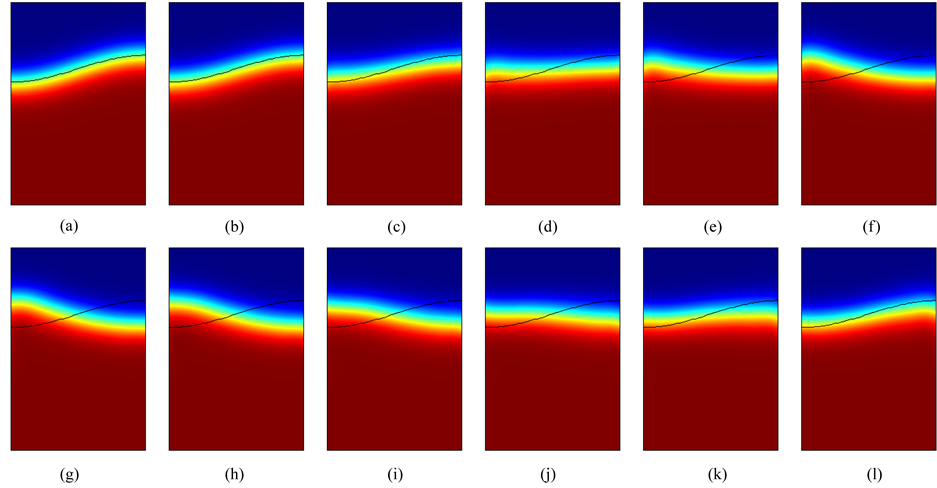
Figure 2. The density field, Re = 1000, At = 0.5. (a) t = 0.0; (b) t = 0.2; (c) t = 0.3; (d) t = 0.35; (e) t = 0.4; (f) t = 0.45; (g) t = 0.5; (h) t = 0.55; (i) t = 0.6; (j) t = 0.65; (k) t = 0.7; (l) t = 0.8.
・ A high Atwood number problem: Setting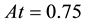

・ A very high Atwood number problem: Setting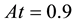
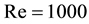

5.3. Rising Bubble Test
To investigate the capability of our method to work with larger density variations, we give the computational results for rising bubble test. This simulation is inspired from [15] [36] - [38] . A light “droplet” rise through a heavy fluid and impacts into the plane surface of the heavy fluid in a cavity. The computational domain is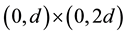
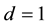
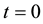
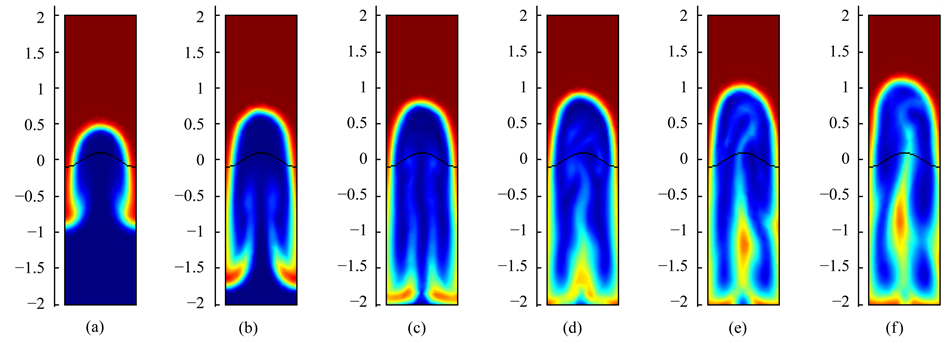
Figure 3. The density field, Re = 1000, At = 0.75. (a) t = 0.2; (b) t = 0.3; (c) t = 0.35; (d) t = 0.4; (e) t = 0.45; (f) t = 0.5.
Figure 4. The density field, Re = 1000, At = 0.9. (a) t = 0.2; (b) t = 0.3; (c) t = 0.35; (d) t = 0.4; (e) t = 0.45; (f) t = 0.5.
where
ing references: 
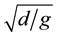

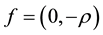

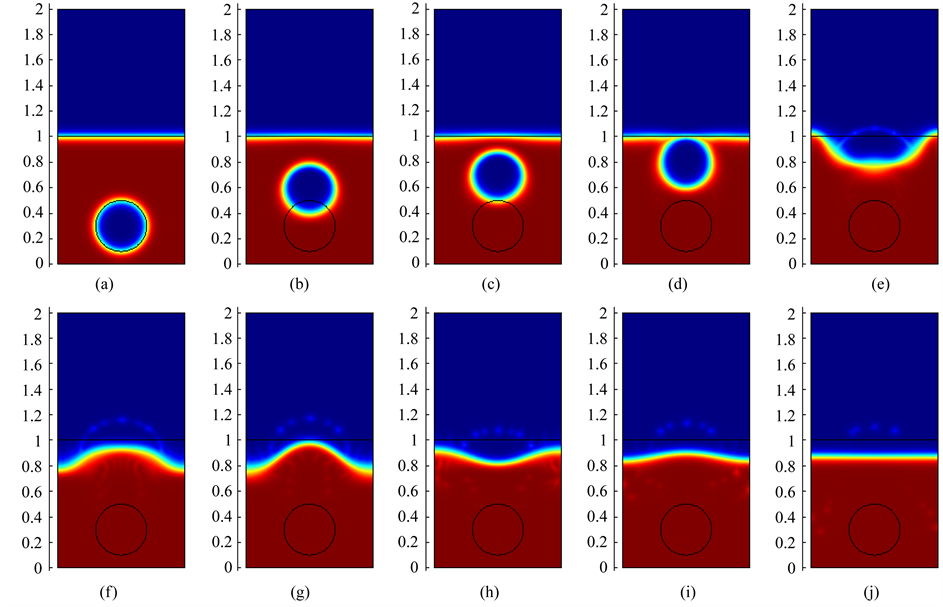
The results are displayed in Figure 5. The figure contain snapshots of the fluid interface. The snapshots show how the “droplet” travels up through a heavy fluid and merges with a light fluid above. As the “droplet” rise, its shape remains spherical due to the surface tension and the viscosity. As the droplet hits the interface, it merges with the light fluid above and creates waves on the surface. The simulation results are satisfactory agreement with the results presented in the literature [15] [36] [37] .
5.4. Sloshing Tank
To investigate the capability of our method to work with very large density variations, a two-fluid flow in a sloshing tank is considered next. The setup of the test case follows the description [37] [39] . The domain 
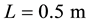
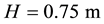
The densities of the fluids are 

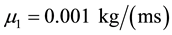
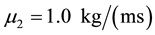
is considered here, so the volume force is
the walls of the tank, and a zero velocity field is initially assumed. The time-step length is 
Figure 5. The density field, Re = 1000. (a) t = 0.0; (b) t = 0.045; (c) t = 0.055; (d) t = 0.065; (e) t = 0.07; (f) t = 0.075; (g) t = 0.08; (h) t = 0.09; (i) t = 0.15.
Figure 6. Sloshing tank: the density field at different times. (a) t = 0.0; (b) t = 0.3; (c) t = 0.6; (d) t = 0.9; (e) t = 1.2; (f) t = 1.5; (g) t = 1.8; (h) t = 2.1; (i) t = 2.4; (j) t = 2.7; (k) t = 3.0; (l) t = 3.3.
The results are displayed in Figure 6. The evolution of the interface at selected points in time. For confir- mation, these patterns may be compared to the respective patterns displayed in Figure 9 in [37] and Figure 15 in [39] , the numerical results are in very good agreement.
6. Conclusions
In this paper, we proposed a characteristics-mix finite element method to the case of incompressible viscous flows with variable density. The originality of our approach is to use different numerical methods for the transport equation and evaluating the evolution of the velocity pressure. The new method uses a time splitting, solving separately the transport equation and the momentum equation. To be more specific, we solve the first equation for a given velocity by using a characteristic stabilized finite element approach which is efficient when dealing with a pure convection equation, and then, we compute the divergence free solution of the last two equations by exploiting the advantages of FE methods. The stability proof of the method we proposed for variable density flows was given in the paper.
To verify the correctness of the method, it has been applied to the test cases previously considered in the literature. The spatial approximation is performed by means of Lagrangian finite elements with P2 interpolation for density and velocity and P1 interpolation for pressure. First, the rates of convergence of the method were proved to be in accordance with the theoretical expected ones, leading so to an accurate solver. Then, the simulation of the viscous Rayleigh-Taylor instability was also investigated. We obtained very good results, even for rather high Atwood numbers. Finally, we considered the rising bubble test and sloshing tank to investigate the robustness property of the scheme with regard to high density ratios. The simulation results coincided with the law of physics are very close to the results presented in the literature. Compared with some established methods, the numerical results show that the new method exhibits good stability behavior even large time steps or the high Atwood numbers are used in computation.
References
- Guermond, J.L. and Salgado, A. (2009) A Splitting Method for Incompressible Flows with Variable Density Based on a Pressure Poisson Equation. Journal of Computational Physics, 228, 2834-2846. http://dx.doi.org/10.1016/j.jcp.2008.12.036
- Pyo, J.H. and Shen, J. (2007) Gauge-Uzawa Methods for Incompressible Flows with Variable Density. Journal of Computational Physics, 221, 181-197. http://dx.doi.org/10.1016/j.jcp.2006.06.013
- Guermond, J.L. and Quartapelle, L. (2000) A Projection FEM for Variable Density Incompressible Flows. Journal of Computational Physics, 165, 167-188. http://dx.doi.org/10.1006/jcph.2000.6609
- Chorin, A.J. (1968) Numeriacl Solution of the Navier-Stokes Equations. Mathematics of Computation, 22, 745-762. http://dx.doi.org/10.1090/S0025-5718-1968-0242392-2
- Chorin, A.J. (1969) On the Convergence of Discrete Approximations to the Navier-Stokes Equations. Mathematics of Computation, 23, 341-353. http://dx.doi.org/10.1090/S0025-5718-1969-0242393-5
- Temam, R. (1977) Navier-Stokes Equations, Studies in Mathematics and Its Applications 2. North-Holland, Amsterdam.
- Temam, R. (1969) Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Archive for Rational Mechanics and Analysis, 33, 377-385. http://dx.doi.org/10.1007/BF00247696
- Guermond, J.L., Minev, P. and Shen, J. (2006) An Overview of Projection Methods for Incompressible Flows. Computer Methods in Applied Mechanics and Engineering, 195, 6011-6045. http://dx.doi.org/10.1016/j.cma.2005.10.010
- Fraigneau, Y., Guermond, J.L. and Quartapelle, L. (2001) Approximation of Variable Density Incompressible Flows by Means of Finite Elements and Finite Volumes. Communications in Numerical Methods in Engineering, 17, 893- 902. http://dx.doi.org/10.1002/cnm.452
- Puckett, G.P., Almgren, A.S., Bell, J.B., Marcus, D.L. and Rider, W. (1997) A High-Order Projection Method for Tracking Fluid Interfaces in Variable Density Incompressible Flows. Journal of Computational Physics, 130, 269-282. http://dx.doi.org/10.1006/jcph.1996.5590
- Buscaglia, G.C. and Codina, R. (2000) Fourier Analysis of an Equal-Order Incompressible Flow Solver Stabilized by Pressure Gradient Projection. International Journal for Numerical Methods in Fluids, 34, 65-92. http://dx.doi.org/10.1002/1097-0363(20000915)34:1<65::AID-FLD56>3.0.CO;2-J
- Bell, J.B. and Marcus, D.L. (1992) A Second Order Projection Method for Variable-Density Flows. Journal of Computational Physics, 101, 334-348. http://dx.doi.org/10.1016/0021-9991(92)90011-M
- Almgren, A.S., Bell, J.B., Colella, P., Howell, L.H. and Welcome, M.L. (1998) A Conservative Adaptive Projection Method for the Variable Density Incompressible Navier-Stokes Equations. Journal of Computational Physics, 142, 1- 46. http://dx.doi.org/10.1006/jcph.1998.5890
- Li, Y., Mei, L., Ge, J. and Shi, F. (2013) A New Fractional Time-Stepping Method for Variable Density Incompressible Flows. Journal of Computational Physics, 242, 124-137. http://dx.doi.org/10.1016/j.jcp.2013.02.010
- Calgaro, C., Creuse, E. and Goudon, T. (2008) An Hybrid Finite Volume-Finite Element Method for Variable Density Incompressible Flows. Journal of Computational Physics, 227, 4671-4696. http://dx.doi.org/10.1016/j.jcp.2008.01.017
- Guermond, J.L. (1999) Stabilization of Galerkin Approximations of Transport Equations by Subgrid Modeling. ESAIM: Mathematical Modelling and Numerical Analysis, 33, 1293-1316. http://dx.doi.org/10.1051/m2an:1999145
- Pyo, J. and Shen, J. (2007) Gauge-Uzawa Methods for Incompressible Flows with Variable Density. Journal of Computational Physics, 221, 181-197. http://dx.doi.org/10.1016/j.jcp.2006.06.013
- Boukir, K. and Maday, Y. (1997) A High-Order Characteristics/Finite Element Method for the Incompressible Navier-Stokes Equations. International Journal for Numerical Methods in Fluids, 25, 1421-1454. http://dx.doi.org/10.1002/(SICI)1097-0363(19971230)25:12<1421::AID-FLD334>3.0.CO;2-A
- Douglas, J., Thomas, F. and Russell, T. (1982) Numerical Method for Convection-Dominated Diffusion Problem Based on Combining the Method of Characteristics with Finite Element of Finite Difference Procedures. SIAM Journal on Numerical Analysis, 19, 871-885. http://dx.doi.org/10.1137/0719063
- Pironneau, O. (1982) On the Transport-Diffusion Algorithm and Its Application to the Navier-Stokes Equations. Numerische Mathematik, 38, 309-332. http://dx.doi.org/10.1007/BF01396435
- Süli, E. (1998) Convergence and Nonlinear Stability of the Lagrange-Galerkin Method for the Navier-Stokes Equations. Numerische Mathematik, 53, 459-483.
- Temam, R. (2001) Navier-Stokes Equations, Theory and Numerical Analysis. Reprint of the 1984 Edition, AMS Chelsea Publishing, Providence.
- Girault, V. and Raviart, P.A. (1986) Finite Element Methods for Navier-Stokes Equations. Springer Series in Computational Mathematics, Vol. 5, Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-61623-5
- Ern, A. and Guermond, J.L. (2004) Theory and Practice of Finite Elements. Applied Mathematical Sciences, Vol. 159, Springer-Verlag, New York. http://dx.doi.org/10.1007/978-1-4757-4355-5
- Adams, R.A. (1975) Sobolev Spaces. Academic Press, New York.
- Evans, L.C. (1998) Partial Differential Equations. American Mathematical Society, Providence.
- Chen, Z. (2005) Finite Element Methods and Their Applications (Scientific Computation). Springer, Berlin.
- Benítez, M. and Bermúdez, A. (2011) A Second Order Characteristics Finite Element Scheme for Natural Convection Problems. Journal of Computational and Applied Mathematics, 235, 3270-3284. http://dx.doi.org/10.1016/j.cam.2011.01.007
- Arbogast, T. and Wheeler, M.F. (1995) A Characteristics-Mixed Finite Element Method for Advection-Dominated Transport-Problems. SIAM Journal on Numerical Analysis, 32, 404-424. http://dx.doi.org/10.1137/0732017
- Turek, S. (1999) Efficient Solvers for Incompressible Flow Problems. Lecture Notes in Computer Science, Springer, Berlin. http://dx.doi.org/10.1007/978-3-642-58393-3
- Codina, R., Blasco, J., Buscaglia, G. and Huerta, A. (2001) Implementation of a Stabilized Finite Element Formulation for the Incompressible Navier-Stokes Equations Based on a Pressure Gradient Projection. International Journal for Numerical Methods in Fluids, 37, 419-444. http://dx.doi.org/10.1002/fld.182
- Dohrmann, C. and Bochev, P. (2004) A Stabilized Finite Element Method for the Stokes Problem Based on Polynomial Pressure Projections. International Journal for Numerical Methods in Fluids, 46, 183-201. http://dx.doi.org/10.1002/fld.752
- He, Y. and Li, J. (2009) Convergence of Three Iterative Methods Based on the Finite Element Discretization for the Stationary Navier-Stokes Equations. Computer Methods in Applied Mechanics and Engineering, 198, 1351-1359. http://dx.doi.org/10.1016/j.cma.2008.12.001
- Guermond, J.L. and Salgado, A.J. (2011) Error Analysis of a Fractional Time-Stepping Technique for Incompressible Flows with Variable Density. SIAM Journal on Numerical Analysis, 49, 917-944. http://dx.doi.org/10.1137/090768758
- Tryggvason, G. (1988) Numerical Simulations of the Rayleigh-Taylor Instability. Journal of Computational Physics, 75, 253-282. http://dx.doi.org/10.1016/0021-9991(88)90112-X
- Schneider, T., Botta, N., Geratz, K.J. and Klein, R. (1999) Extension of Finite Volume Compressible Flow Solvers to Multidimensional Variable Density Zero Mach Number Flows. Journal of Computational Physics, 155, 248-286. http://dx.doi.org/10.1006/jcph.1999.6327
- Rasthofer, U., Henke, F., Wall, W.A. and Gravemeier, V. (2011) An Extended Residual-Based Variational Multiscale Method for Two-Phase Flow Including Surface Tension. Computer Methods in Applied Mechanics and Engineering, 200, 1866-1876. http://dx.doi.org/10.1016/j.cma.2011.02.004
- Fries, T.P. (2010) Level Set Method for Two-Phase Incompressible Flows under Magnetic Fields. Computer Physics Communications, 181, 999-1007. http://dx.doi.org/10.1016/j.cpc.2010.02.002
- Fries, T.P. (2009) The Intrinsic XFEM for Two-Phase Flows. International Journal for Numerical Methods in Fluids, 60, 437-471. http://dx.doi.org/10.1002/fld.1901