Advances in Pure Mathematics
Vol.06 No.10(2016), Article ID:70530,9 pages
10.4236/apm.2016.610053
Solutions to Beal’s Conjecture, Fermat’s Last Theorem and Riemann Hypothesis
A. C. Wimal Lalith de Alwis
School of Four Incalculables and Tathagatha’s Society No. 299, Moratuwa, Sri Lanka

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: March 15, 2016; Accepted: September 10, 2016; Published: September 13, 2016
ABSTRACT
A Simple Mathematical Solutions to Beal’s Conjecture and Fermat’s Marginal Conjecture in his diary notes, Group Theoretical and Calculus Solutions to Fermat’s Last theorem & Integral Solution to Riemann Hypothesis are discussed.
Keywords:
Beal’s Conjecture, Fermat’s Last Theorem, Riemann Hypothesis

1. A Solution to Beal’s Conjecture
Beal’s conjecture states if 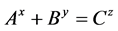 where
where 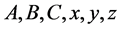 are positive integers,
are positive integers, 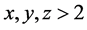 then
then 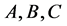 have a common prime factor.
have a common prime factor.
Since it is a conjecture it should either be proved or disproved so that we have to find simple way to handle it. In the search of a solution to the open problem after many trial and errors we decided to tackle it in the following way. Take
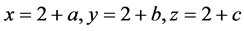 where
where 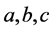 are positive integers then
are positive integers then
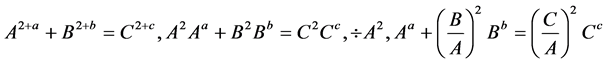 since
since 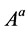 is a
is a
positive integer the square coefficient factors appearing in the left hand side of  and
and 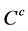 cannot be fractions any more so that B and C must be divisible by A. Under the present circumstances either
cannot be fractions any more so that B and C must be divisible by A. Under the present circumstances either 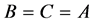 or
or 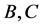 must have A as common factor. That is the general proof that could be developed and we have to come up with numerical solutions & in its search it is possible to give a simple example. Take
must have A as common factor. That is the general proof that could be developed and we have to come up with numerical solutions & in its search it is possible to give a simple example. Take
 the lowest prime number and 1 is not a prime number. So
the lowest prime number and 1 is not a prime number. So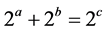 ,
,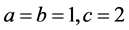 is a solution. Further
is a solution. Further 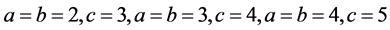 and in general
and in general  for all
for all 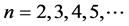 and so on & 2 must be a pri- me factor conjectured by Beal. The example suggested is within the theory formulated.
and so on & 2 must be a pri- me factor conjectured by Beal. The example suggested is within the theory formulated.
Further ![]() satisfy Beal’s Conjecture. If we generalize it
satisfy Beal’s Conjecture. If we generalize it ![]() in this case prime factor is 3, countably infinite number of examples are satisfying the Beal’s Conjecture a different example. The series that we have introduced before is
in this case prime factor is 3, countably infinite number of examples are satisfying the Beal’s Conjecture a different example. The series that we have introduced before is ![]()
![]()
![]() not satisfying Beal’s Conjecture,
not satisfying Beal’s Conjecture,
![]()
![]() all, the entire set of countably infinite number of examples well agree with Beal’s Conjecture was questioned by W. Naduna Child Student of our School that gave foundation to our investigation on what is said to be known as Beal’s Conjecture. What we have given is minimally sufficient to prove Beal’s Conjecture. This is an exposition in the field of basic mathematics education rather than rigor and abstractness that leads to unreadability.
all, the entire set of countably infinite number of examples well agree with Beal’s Conjecture was questioned by W. Naduna Child Student of our School that gave foundation to our investigation on what is said to be known as Beal’s Conjecture. What we have given is minimally sufficient to prove Beal’s Conjecture. This is an exposition in the field of basic mathematics education rather than rigor and abstractness that leads to unreadability. ![]() are interesting number identities observed by Indian Mathematical Genius Ramanujan [1] , [2] .
are interesting number identities observed by Indian Mathematical Genius Ramanujan [1] , [2] .
There are bigger five set of number identities given by Don Zagier but non of them fit with Beal’s Conjecture due to Beal’s restriction all ![]() exponents must be greater than 2 then only such
exponents must be greater than 2 then only such ![]() must be divisible by a prime number such as
must be divisible by a prime number such as
![]() So far none other primes could be found as satisfying Beal’s conjecture other than 2, 3 prime numbers which are the smallest 1 is not prime. It is difficult to expect more than what is said. But Robert Kanigel [2] in page 343 under the paragraph three states in his novel book on Srinivasa Ramanujan [2] “Let
So far none other primes could be found as satisfying Beal’s conjecture other than 2, 3 prime numbers which are the smallest 1 is not prime. It is difficult to expect more than what is said. But Robert Kanigel [2] in page 343 under the paragraph three states in his novel book on Srinivasa Ramanujan [2] “Let ![]() denote the sum of the sth powers of divisors of n”, Ramanujan had begun. If n = 6 for example, its divisors are 6, 3, 2 and 1. So that if, say 3, “the sum of the sth powers of the divisors”,
denote the sum of the sth powers of divisors of n”, Ramanujan had begun. If n = 6 for example, its divisors are 6, 3, 2 and 1. So that if, say 3, “the sum of the sth powers of the divisors”, ![]() is just
is just ![]() But how to calculate
But how to calculate ![]() generally? that question led Ramanujan, after fifteen pages, to the tau function, whose properties, Hardy would write twenty years later, “are very remarkable and still very imperfectly understood”. As in so much of analytical number theory, stepping through the open door of a simple- seeming problem had led into a mathematical labyrinth of formidable complexity.
generally? that question led Ramanujan, after fifteen pages, to the tau function, whose properties, Hardy would write twenty years later, “are very remarkable and still very imperfectly understood”. As in so much of analytical number theory, stepping through the open door of a simple- seeming problem had led into a mathematical labyrinth of formidable complexity.
Now let us get back to our answering based on what is said by Robert Kanigel [2] on some piece of work by Mathematical Genius Ramanujan
![]() the second example that coincided with Beal’s Conjecture that we have already noted. So rest also must be derivable from Ramanujan’s work commented by Robert Kanigel [2] a Great Novelist historian in mathematics of Srinivasa Iyengar Ramanujan and his life. Answer to Beal’s Conjecture must fall from Goddess Namagiri of Namakkal the Ramanujan’s Divine dietyof great faith in the state of Tamilnadu in India the southern part of land of ancient Barat Now consider
the second example that coincided with Beal’s Conjecture that we have already noted. So rest also must be derivable from Ramanujan’s work commented by Robert Kanigel [2] a Great Novelist historian in mathematics of Srinivasa Iyengar Ramanujan and his life. Answer to Beal’s Conjecture must fall from Goddess Namagiri of Namakkal the Ramanujan’s Divine dietyof great faith in the state of Tamilnadu in India the southern part of land of ancient Barat Now consider
![]()
satisfying Beal’s Conjecture could be derived from sum of 1th powers of divisors of 2n−1 including 1 and itself, based on the mathematics of Ramanujan’s paper on certain arithmetical functions appeared in the transactions of the Cambridge Philosophical Society, XX11, No. 9, 1916, 159 - 184. If other number identities exist they all might be derivable by the same technique introduced here at last a genuine approach to finalize the story. Further
![]()
n = 4,15 is not a prime factor, n = 6,63 is not a prime factor are very simple counter examples to Beal’s Conjecture, So it is very clear factor need not be prime always but can be prime or not prime. Very simple mathematics founded by W. Nadun, Kanigel, S. Ramanujan at last but not least defeated Beal’s Claim of a prime factor always for exponents greater than 2 for Beal-Fermat Equation a generalization of Fermat’s Theorem at Last and Beal’s Theorem at First. Andrew Beal was very sincere if at least few counter examples are found for his famous conjecture now he is provided with two such cases. If you computerize it with a programming language it may give many counter examples as well as examples satisfying Beal. In our discussion, we end this story on Beal’s Conjecture. Wikipedia on Beal can provide more information. We have provided sufficient ground in support of Beal’s Conjecture as well as against it.
2. A Solution to Fermat’s Marginal Conjecture in His Diary Notes
![]() there are no positive integers for
there are no positive integers for ![]() recorded by Fermat.
recorded by Fermat.
Now assume there are such positive integer ![]() with no common factors satisfying Fermat’s Conjecture given for
with no common factors satisfying Fermat’s Conjecture given for ![]() and take
and take
![]()
since ![]() are positive integers, contradicting the original assumption of no common factors so such
are positive integers, contradicting the original assumption of no common factors so such ![]() positive integers cannot exist for the given equation confirming Fermat’s marginal diary note. First we assumed that, there are positive integers with no common factors for higher n than two for the Fermat’s Equation that we have started with. Later with that assumption we could be able to come to a conclusion mathematically x is a multiple of y and z that contradict our own assumption of no common multiples. Due to the contradiction that we could have obtained we decided our original assumption of existence of positive integers with no common multiples is incorrect for higher n than two. This is famous reduction ad absurdum that is method of reduction to absurdity introduced by Pythagoras a logical deduction methodology. It has sufficient ground for a simple proof as expected by Fermat what he said is that, the proof is very simple but he does not have sufficient space to write it in his marginal diary note. The case of m equal to one provides a clear comprehension of the logic behind. It provides the missing ground of a simple proof as said by Fermat himself unnoticed before and when proofs are too long readers drop it.
positive integers cannot exist for the given equation confirming Fermat’s marginal diary note. First we assumed that, there are positive integers with no common factors for higher n than two for the Fermat’s Equation that we have started with. Later with that assumption we could be able to come to a conclusion mathematically x is a multiple of y and z that contradict our own assumption of no common multiples. Due to the contradiction that we could have obtained we decided our original assumption of existence of positive integers with no common multiples is incorrect for higher n than two. This is famous reduction ad absurdum that is method of reduction to absurdity introduced by Pythagoras a logical deduction methodology. It has sufficient ground for a simple proof as expected by Fermat what he said is that, the proof is very simple but he does not have sufficient space to write it in his marginal diary note. The case of m equal to one provides a clear comprehension of the logic behind. It provides the missing ground of a simple proof as said by Fermat himself unnoticed before and when proofs are too long readers drop it.
3. A Solution to Fermat’s Last Theorem Found in 1982-1983 Period by Galois Theory of Groups
Fermat’s Last Theorem states ![]() does not have positive integer solutions for
does not have positive integer solutions for![]() . Take
. Take ![]() &
& ![]() are positive integers. Then
are positive integers. Then ![]() and expand by Newton’s Binomial Theorem and bring all ter- ms to the left hand side keeping right hand side zero. By Abel-Galois Theory it is not solvable by radicals for
and expand by Newton’s Binomial Theorem and bring all ter- ms to the left hand side keeping right hand side zero. By Abel-Galois Theory it is not solvable by radicals for ![]() which are quantic or higher order polynomial equations so no roots can be extracted for this general equation the existence of positive integer solutions cannot be predicted. In general no information can be retrieved in this regard from higher order polynomials whose degree is greater than 4. But for
which are quantic or higher order polynomial equations so no roots can be extracted for this general equation the existence of positive integer solutions cannot be predicted. In general no information can be retrieved in this regard from higher order polynomials whose degree is greater than 4. But for ![]() this transformation can be used to tackle the non-existence of integer solutions and for n = 2 this leads to the Pythagorean triplets. It is not difficult to work out the advance details and abstract algebra needed are well available in text books [3] , [4] .
this transformation can be used to tackle the non-existence of integer solutions and for n = 2 this leads to the Pythagorean triplets. It is not difficult to work out the advance details and abstract algebra needed are well available in text books [3] , [4] .
Few technical points can be noted as follows. The resulting polynomial equation is
![]() where
where
![]() are the roots
are the roots
![]()
![]() is the elementary symmetric function.
is the elementary symmetric function. ![]() is the coefficient of
is the coefficient of ![]() in the polynomial
in the polynomial![]() .
.
![]()
be the elementary symmetric functions in the in-determinates ![]() then every symmetric function in
then every symmetric function in ![]() over F is a rational function of the elementary symmetric functions. Also,
over F is a rational function of the elementary symmetric functions. Also, ![]() is a finite normal extension of
is a finite normal extension of ![]() of degree
of degree ![]() and the Galois group of this ex- tension is isomorphic to
and the Galois group of this ex- tension is isomorphic to![]() . Let G be a finite group, with identity element
. Let G be a finite group, with identity element![]() , G is said to be a Solvable group if there exists a Sequence of Subgroups
, G is said to be a Solvable group if there exists a Sequence of Subgroups
![]() Such that for
Such that for ![]()
![]() is a Normal Subgroup of G with an Abelian Factor Group. For quadratic equation Galois Group
is a Normal Subgroup of G with an Abelian Factor Group. For quadratic equation Galois Group ![]() consists of the identity and a map interchanging
consists of the identity and a map interchanging![]() . For cubic equation the Galois group
. For cubic equation the Galois group ![]() has a series
has a series ![]() with Abelian quotients.
with Abelian quotients.
For quartic equation the Galois group ![]() has a series
has a series ![]() with abelian quotients where
with abelian quotients where![]() .
.
Therefore ![]() are solvable so that corresponding quadratic, cubic, quartic equations are solvable by radicals.
are solvable so that corresponding quadratic, cubic, quartic equations are solvable by radicals.
Alternating Group![]() ,
, ![]() has no normal subgroups whatever except itself and identity. Therefore Symmetric Group
has no normal subgroups whatever except itself and identity. Therefore Symmetric Group![]() , is not solvable if
, is not solvable if![]() . Thus, any polynomial whose Galois Group [5] is
. Thus, any polynomial whose Galois Group [5] is ![]() is not solvable by radicals.
is not solvable by radicals.
Therefore for ![]() no radical solutions for
no radical solutions for ![]() exists so no inte- ger solutions for x are derivable radically for this general form of the equation. It has sufficient base of a proof not noticed before.
exists so no inte- ger solutions for x are derivable radically for this general form of the equation. It has sufficient base of a proof not noticed before.
As ![]() produce Pythagorean triplets we have found
produce Pythagorean triplets we have found
![]() gives rise to them as an example take p = 0 leads to
gives rise to them as an example take p = 0 leads to ![]() the first Pythagorean triplet. This new formula was discovered by us using the technique introduced here at the beginning.
the first Pythagorean triplet. This new formula was discovered by us using the technique introduced here at the beginning.
4. A Marginal Proof for Fermat’s Last Theorem by Calculus
Start with ![]() and differentiate it with respect to x.
and differentiate it with respect to x.
![]()
when
![]()
![]() is the discriminant
is the discriminant ![]()
![]() for real roots to exists where
for real roots to exists where ![]() are assumed to be positive inte-
are assumed to be positive inte-
gers, consider the case with ![]() so that
so that
![]()
leads to complex number ![]() which ends up in a contradiction due to the original assumption of existence of positive integer
which ends up in a contradiction due to the original assumption of existence of positive integer ![]() for Fermat’s equation.
for Fermat’s equation.
![]()
![]()
Therefore by the method called Reductio ad Absurdum that is reduction to absurdity Fermat’s Criteria get satisfied that there are no positive integer solutions when ![]() for the Fermat’s Conjectural Equation
for the Fermat’s Conjectural Equation![]() . This is a marginal proof that is a very short exposition that was expected by Fermat in his original diary notes.
. This is a marginal proof that is a very short exposition that was expected by Fermat in his original diary notes.
![]() so there is a maxima at
so there is a maxima at
this point but does not exist due tonon availability of real positive integers for zero discriminant that must be what Frey has stated as forbidden of existence.
Further ![]() for
for ![]() For
For ![]() Frey’s Curve with the starting formula
Frey’s Curve with the starting formula ![]() forbidden to exist & it cannot be plotted with Fermat’s conditions under the circumstances arose. Reductio ad Absurdum that is reducing to absurdity the logical deduction methodology was used. Related advance material are well available in the current mathematical literature only missing parts are noted in our exposition to avoid unreadability. It has sufficient ground to simplify the proof.
forbidden to exist & it cannot be plotted with Fermat’s conditions under the circumstances arose. Reductio ad Absurdum that is reducing to absurdity the logical deduction methodology was used. Related advance material are well available in the current mathematical literature only missing parts are noted in our exposition to avoid unreadability. It has sufficient ground to simplify the proof.
5. Proof of Riemann Hypothesis
A proof is given for the Riemann Hypothesis in the strictly open interval ![]() and further it is proved what exactly happens on the boundary lines at
and further it is proved what exactly happens on the boundary lines at ![]() in the closed interval
in the closed interval![]() .
.
![]()
is the Riemann Zeta function, ![]() are the real and imaginary parts of a Complex Num-
are the real and imaginary parts of a Complex Num-
ber. What Hypothesis says is that ![]() only on
only on ![]() line in the open interval
line in the open interval
![]()
![]() .
.
In theory of Complex Numbers ![]() Similarly
Similarly
![]() Question: For which value of
Question: For which value of![]() ?,
?,![]() . Take
. Take
![]()
and with the substitution at relevant places in I & J integrals we get for ![]()
![]() for choice of
for choice of
![]() that is for half value of
that is for half value of ![]() a natural selection of a value for
a natural selection of a value for ![]()
what values I and J integrals take?
![]() .
.
![]() . Since Sine and Cosine are periodic
. Since Sine and Cosine are periodic
trigonometric functions.
![]()
![]() Therefore
Therefore ![]() for arbitrary t on
for arbitrary t on ![]() line in the open interval
line in the open interval ![]()
![]() on
on ![]() line in the range
line in the range
![]() that is for all values of t.
that is for all values of t.
This completes the proof which has sufficient ground unnoticed before for the long awaited Riemann Hypothesis strictly in the open interval ![]() conjectured by Bernhard Riemann a German Mathematician who found the Riemann definition of Integral & Riemann Geometry used by Albert Einstein in the formulation of General Theory of Relativity. Further it is worth to mention something more than Riemann that did not appear under his conjecture that he has missed at his time for the benefit of mathematics
conjectured by Bernhard Riemann a German Mathematician who found the Riemann definition of Integral & Riemann Geometry used by Albert Einstein in the formulation of General Theory of Relativity. Further it is worth to mention something more than Riemann that did not appear under his conjecture that he has missed at his time for the benefit of mathematics
![]() &
& ![]() we keep them for readers
we keep them for readers
to come up with their sketch of proofs following similar line of thought the existence of two more zero lines and beyond this closed range no more such lines exists.
Acknowledgements
These problems were newly proposed by A. C. Ranjith De Alwis at E-Mail: charles@hansexportaustralia.com.au, due to the announcement of new awards by Clay Institute up to seven million US Dollars appearing in the internet web can be found under Google search where Edward Witten, Andrew Wile … are Founding Members and Solved by A. C. Wimal Lalith De Alwis present author assisted by W. Nadun, Susitha S. Present Author [another E-Mail: dealwis_a@yahoo.com, Home Address: No. 299, Galle Road, Goraka, Moratuwa] the author of new principia is staying in Lanka the Golden Lanka of Ramayan Epicand National Aeronautical Space Agency of America (NASA) found high rock peaks & their height up to 20,000 feets in Adams Bridge path from Talaimannar of Lanka to Danushkodi of India by Geographical Earth satellite over length of 35 km strip that India is going to cover the sea gap by Rama Sethu Bridge project with assistance of NASA if not by Stones by Cables.
Cite this paper
de Alwis, A.C.W.L. (2016) Solutions to Beal’s Conjecture, Fermat’s Last Theorem and Riemann Hypothesis. Advances in Pure Mathematics, 6, 638- 646. http://dx.doi.org/10.4236/apm.2016.610053
References
- 1. Hardy, G.H., Seshu Aiyar, P.V. and Wilson, B.M. (1927) Collected Papers of Srinivasa Ramanujan. Cambridge at the University Press, Cambridge.
- 2. Kanigel, R. (1992) The Man Who Knew Infinity, A Life of Genius Ramanujan. Hard Cover Edition, Rupa & Co. Bombay.
- 3. Bhattacharya, P.B., Jain. S.K. and Nagpaul, S.R. (1995) Basic Abstract Algebra. 1st Indian Edition, Cambridge University Press, New Delhi.
- 4. van der Poorten, A. (1996) Notes on Fermat’s Last Theorem. John Wiley and Sons, Inc., Brisbane.
- 5. Galois Theory by Ian Stewart (2003) 3rd Edition, Chapman and Hall/CRC, A CRC Press Company, Boca Raton.





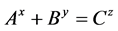 where
where 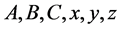 are positive integers,
are positive integers, 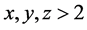 then
then 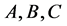 have a common prime factor.
have a common prime factor.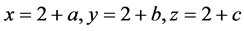 where
where 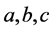 are positive integers then
are positive integers then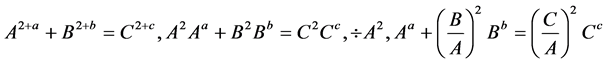 since
since 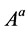 is a
is a and
and 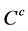 cannot be fractions any more so that B and C must be divisible by A. Under the present circumstances either
cannot be fractions any more so that B and C must be divisible by A. Under the present circumstances either 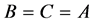 or
or 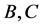 must have A as common factor. That is the general proof that could be developed and we have to come up with numerical solutions & in its search it is possible to give a simple example. Take
must have A as common factor. That is the general proof that could be developed and we have to come up with numerical solutions & in its search it is possible to give a simple example. Take the lowest prime number and 1 is not a prime number. So
the lowest prime number and 1 is not a prime number. So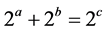 ,
,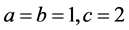 is a solution. Further
is a solution. Further 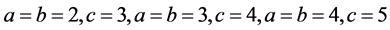 and in general
and in general  for all
for all 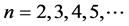 and so on & 2 must be a pri- me factor conjectured by Beal. The example suggested is within the theory formulated.
and so on & 2 must be a pri- me factor conjectured by Beal. The example suggested is within the theory formulated.
























































































































