Received 26 February 2015; accepted 13 March 2015; published 19 March 2015

ABSTRACT

The aim of this paper is to find the formula for the elementary operations on L-R fuzzy number. In this paper we suggest and describe addition, subtraction, multiplication and division of two L-R fuzzy numbers in a brief.

Keywords:

Fuzzy Number, L-R Fuzzy Number, Membership Function

1. Introduction

A fuzzy set [1] A on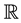, set of real numbers is called a fuzzy number [2] which satisfies at least the following three properties:

1) must be a normal fuzzy set [3] .

2) 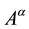must be a closed interval for every.

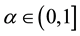3) The support [1] of A, must be bounded.

The fundamental idea of the L-R representation of fuzzy numbers is to split the membership function 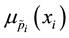of a fuzzy number 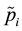into two curves 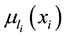and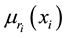, left and right of the modal value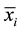. The membership function 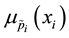can be expressed through parameterized reference functions or shape function L and R in the form

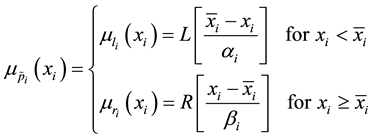(1)

where 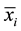is the modal value of the membership function 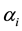and and 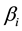are the spreads corresponding to the left-hand and right-hand curve of the membership function [4] respectively.

As an abbreviated notation, we can define an L-R fuzzy number 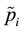with the membership function in (1) by

(2)

where the subscripts L and R specify the reference functions [5] .

2. Operations on L-R Fuzzy Number

In this section, the formulas for the elementary operations (addition, subtraction, multiplication, division) [5] between L-R fuzzy numbers [5] will be presented.

2.1. Addition of L-R Fuzzy Number

Suppose two fuzzy numbers and, represented as L-R fuzzy numbers of the form

(3)

The sum is again an L-R fuzzy number of the form

(4)

with the modal value

(5)

and the spreads

(6)

In short we can write

(7)

The left-hand reference functions of both fuzzy numbers and have to be given by L, and the right- hand reference functions by R.

The formula of the L-R addition in (7) is motivated by the following ways:

We first consider the right-hand curves and of the L-R fuzzy numbers and with

(8)

The degree of membership is taken on for the argument values

(9)

This implies

(10)

and we obtain for the right-hand curve of the fuzzy number

(11)

The same reasoning holds for the left-hand curves of, and, and we get

(12)

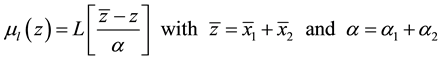
2.2. Subtraction of L-R Fuzzy Number

Suppose two fuzzy numbers and, represented as L-R fuzzy numbers of the form

(13)

The opposite of the L-R fuzzy number is defined as

(14)

Now by using (7) we can deduce the following formula for the subtraction of the L-R fuzzy numbers:

(15)

2.3. Multiplication of L-R Fuzzy Number

Let us consider two positive fuzzy numbers and of the same L-R type given by the L-R representations

(16)

We can construct the right-hand curve of the product on the basis of the right-hand curves

(17)

of L-R fuzzy numbers and. In accordance with the deduction of the formula for the L-R addition, the degree of membership is taken on for the argument values

(18)

This implies

(19)

Two approximations have been proposed, which is referred to as tangent approximation and secant approximation in the following:

2.3.1. Tangent Approximation

Let and are small compared to and and is in the neighborhood of 1. Then we can neglect the quadratic term in (19) and we obtain for the right-hand curve of the approximated product an expression of the form

(20)

Using the same reasoning for the left-hand curves of, and, we deduce the following formula for the multiplication of L-R fuzzy numbers

(21)

2.3.2. Secant Approximation

If the spreads are not negligible compared to the modal values and, the rough shape of the product

can be estimated by approximating quadratic term in (19) by the linear term

. This gives the right-hand curve of the approximated product in the form

(22)

With the same reasoning for the left-hand curves of, and, the overall formula for the multiplication of L-R fuzzy numbers results in

(23)

2.4. Division of L-R Fuzzy Number

An appropriate formulation for the quotient of two L-R fuzzy numbers and can be obtained by reducing the division of the fuzzy numbers and to the multiplication of the dividend with the inverse of the divisor.

When we consider a fuzzy number which is either positive or negative, i.e., , given by the L-R representation

the tangent approximation for the inverse is defined by

and the secant approximation by

Using the above mentioned identity as well as the approximation formulas for the multiplication of L-R fuzzy numbers on one side and those for the inverse of an L-R fuzzy number on the other, a number of different approximated L-R representations for the quotient can be formulated.

3. Example

We consider two L-R fuzzy number

Then using Equation (7) we get

Also can be written in the form

Using (15) we get

Also can be written in the form

If we use the tangent approximation the product is approximated by the triangular L-R fuzzy number

Again in the case of secant approximation the result is approximated by

If we use the tangent approximation the inverse is approximated by the triangular L-R fuzzy number

Thus

But if we use the secant approximation the inverse is approximated by the triangular L-R fuzzy number

Thus

4. Conclusion

In this paper we have presented exact calculation formulas for addition, subtraction, multiplication and division of two L-R fuzzy numbers. Finally we have taken two L-R fuzzy numbers as an example and obtained results of addition, subtraction, multiplication and division. We have reviewed some research papers with proper references.

References