Received 1 December 2014; revised 15 December 2014; accepted 1 January 2015

ABSTRACT

Fractional integral of continuous functions has been discussed in the present paper. If the order of Riemann-Liouville fractional integral is v, fractal dimension of Riemann-Liouville fractional inte- gral of any continuous functions on a closed interval is no more than 2 − v.

Keywords:

Box Dimension, Riemann-Liouville Fractional Calculus, Fractal Function

1. Introduction

In [1] , fractional integral of a continuous function of bounded variation on a closed interval has been proved to still be a continuous function of bounded variation. The upper bound of Box dimension of the Weyl-Marchaud fractional derivative of self-affine curves has given in [2] . Previous discussion about fractal dimensions of fractional calculus of certain special functions can be found in [3] [4] .

In the present paper, we discuss fractional integral of fractal dimension of any continuous functions on a closed interval.

If U is any non-empty subset of n-dimensional Euclidean space, 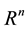, the diameter of U is defined as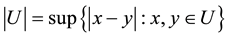, i.e. the greatest distance apart of any pair of points in U. If 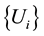is a countable collection of sets of diameter at most δ that cover F, i.e. 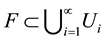with 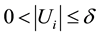for each i, we say that 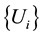is a δ-cover of F.

Suppose that F is a subset of 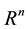and s is a non-negative number. For any positive number define

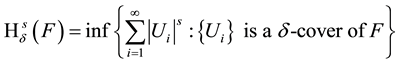
Write

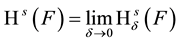
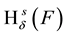is called s-dimensional Hausdorff measure of F. Hausdorff dimension is defined as follows:

Definition 1.1 [5] Let F be a subset of 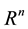and s is a non-negative number. Hausdorff dimension of F is

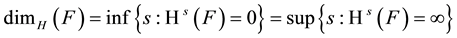
If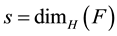, then 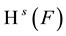may be zero or infinite, or may satisfy

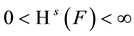
A Borel set satisfying this last condition is called an s-set.

Box dimension is given as follows:

Definition 1.2 [5] Let F be any non-empty bounded subset of 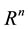and let be the smallest number of sets of diameter at most which can cover F. Lower and upper Box dimensions of F respectively are defined as

(1.1)

and

(1.2)

If (1.1) and (1.2) are equal, we refer to the common value as Box dimension of F

(1.3)

Definition 1.3 [6] Let and. For we call

Riemann-Liouville integral of of order v.

2. Riemann-Liouville Fractional Integral of 1-Dimensional Fractal Function

Let be a 1-dimensional fractal function on I. We will prove that Riemann-Liouville fractional integral of is bounded on I. Box dimension of Riemann-Liouville fractional integral of will be estimated.

2.1. Riemann-Liouville Fractional Integral of

Theorem 2.1 Let be Riemann-Liouville integral of of order v. Then, is bounded.

Proof. Since is continuous on a closed interval I, there exists a positive constant M such that

From Definition 1.3, we know

For any, it holds

is a bounded function on I.

2.2. Fractal Dimensions of Riemann-Liouville Fractional Integral of

Theorem 2.2 Let be Riemann-Liouville integral of of order v. Then,

Proof. Let, and m is the least integer greater than or equal to. If, we have

For, let, If

, it holds

If, it holds

We have

Let. If, we have

If, it holds

If, it holds

We get

There exists a positive constant C, such that

If is the number of squares of the mesh that intersects, by Proposition 11.1 of [1] , we have

From (1.2) of Definition 1.2, we know

With Definition 1.1, we get the conclusion of Theorem 2.2.

This is the first time to give estimation of fractal dimensions of fractional integral of any continuous function on a closed interval.

Acknowledgements

Research is supported by NSFA 11201230 and Natural Science Foundation of Jiangsu Province BK2012398.

References