Advances in Pure Mathematics
Vol.04 No.12(2014), Article ID:52405,7 pages
10.4236/apm.2014.412073
From Highly Structured E-Infinity Rings and Transfinite Maximally Symmetric Manifolds to the Dark Energy Density of the Cosmos
Mohamed S. El Naschie
Department of Physics, University of Alexandria, Alexandria, Egypt
Email: Chaossf@aol.com
Academic Editor: Leila Marek-Crnjac, Technical School Center, Maribor, Slovenia
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 8 November 2014; revised 5 December 2014; accepted 12 December 2014
ABSTRACT
Starting from well established results in pure mathematics, mainly transfinite set theory, E-infi- nity algebra over operads, fuzzy manifolds and fuzzy Lie symmetry groups, we construct an exact Weyl scaling for the highly structured E-infinity rings corresponding to E-infinity theory of high energy physics. The final result is an exact expression for the energy density of the cosmos which agrees with previous analysis as well as accurate cosmological measurements and observations, such as COBE, WMAP and Planck. The paper is partially intended as a vivid demonstration of the power of pure mathematics in physics and cosmology.
Keywords:
Highly Structured Rings, E-Infinity, Loop Spaces, High Energy Physics, Dark Energy, Einstein Relativity, Fractal-Cantorian Spacetime, Nonlinear Dynamics, Quantum Chaos

1. Introduction
There are a few scientists, the present author included, who feel quite strongly that at its deepest level physics in general and high energy particle physics in particular is governed by the laws of pure mathematics [1] -[5] , that is to say the laws of thought. Thus pure mathematics could be seen as the foundation of the very roots of real physics to the extent that any true mathematical theorem, no matter how pure it is, will very likely have an application in the so called “real world” domain [5] - [25] . The present author believes that the work of L. Euler, F. Gauss, J. von Neumann, A. Connes as well as E-infinity theory are accurate examples for this scientific philosophy [1] - [62] .
The main purpose of the present paper is twofold. It is intended first to make the mainstream applied physicists more aware of the treasures of pure mathematics waiting to be discovered by them for application [53] - [62] and second to make pure mathematicians more aware of the indispensible role played by their pure science in applied sciences, particularly high energy physics and quantum cosmology [60] - [62] . The present author thinks, and so do others, that his main contribution was to help bring E-infinity theory and related areas such as transfinite numbers and Cantorian fractals to quantum physics and cosmology [24] - [42] . The Klein-Penrose fractal universe [40] which is used here directly and indirectly, is a clear cut example of noncommutative geometry as well as being a prototype of K-theory and Cantorian-E-infinity theory [12] [40] . Noting the well known intimate relationship of K-theory, n-categories and E-infinity algebra over operads [42] [43] and the associated loop spaces and E-infinity spectra, the reader can sense the deep relations between E-infinity Cantorian spacetime of high energy physics on the one side and the afore mentioned enormously rich and versatile fields of pure mathematics. In fact, as mentioned earlier, from the viewpoint of the present work, the basis of the foundation of theoretical quantum physics and cosmology, is without a doubt, pure mathematics [9] [10] . The author seriously believes that any mathematically consistent structure in pure mathematics corresponds to something out there in the real world so that the division between pure mathematics and physics is a largely an artificial one.
The present paper will use transfinite set theoretical results [7] and results from K-theory and E-infinity theory and demonstrate that dark energy and ordinary energy apart from quantum wave collapse and measurement can be fully understood [60] - [62] .
2. A Transfinite Cellular Automata as a Golden Turing
The main pillar upon which our highly structured E-infinity golden ring [42] [43] rests is the golden mean “binary” system. Before going into that we recall first a few facts concerning E-infinity in general. First  ring is a commutative monad in the
ring is a commutative monad in the 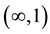 -category of E-infinity spectra. E-infinity algebra on the other hand is an algebra over an operad for E-infinity operad [42] [43] . In chain complex this is similar, in fact equivalent to those in Abelonian symplectical group which brings us nearer to our treatment of the compactified symplectic modular space of Klein and Penrose [38] [40] . For our present E-infinity “physical” version of P. May E-infinity, the golden mean ring introduces incredible simplification to the entire problem [11] so that the E-infinity algebra
-category of E-infinity spectra. E-infinity algebra on the other hand is an algebra over an operad for E-infinity operad [42] [43] . In chain complex this is similar, in fact equivalent to those in Abelonian symplectical group which brings us nearer to our treatment of the compactified symplectic modular space of Klein and Penrose [38] [40] . For our present E-infinity “physical” version of P. May E-infinity, the golden mean ring introduces incredible simplification to the entire problem [11] so that the E-infinity algebra
is de facto replaced by an almost elementary E-infinity arithmetic manipulating 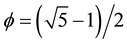 in all its forms
in all its forms
of union and intersections in a way analogous to a Suslin operation. For instance the vital  is found from [11] [35] [37]
is found from [11] [35] [37]
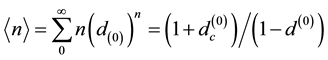 (1)
(1)
to be nothing but
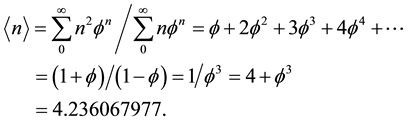 (2)
(2)
Similarly one finds that the same value is obtained for the average Hausdorff dimension [11] [35] [37]
 (3)
(3)
The above constitutes the required minimum to understand the rest of the paper which is devoted to a major cosmological problem considered by many as the greatest mystery of our time [63] .
3. Analysis of the Energy Density of the Cosmos
We start from the obvious fact that Einstein’s space is 4 dimensional, i.e. 3 spatial dimensions fused to 1 time dimension and that the classical photon of the electromagnetic field moves in these 4 dimensions [56] [57] [59] . At least formally, Einstein’s density could be given within this picture as the ratio of the spacetime background dimension  to itself as the dimension of the photon “space” so that we obtain the trivial result
to itself as the dimension of the photon “space” so that we obtain the trivial result
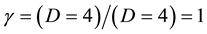 (4)
(4)
and the corresponding Einstein special relativity formula is again formally given by the trivial tautology
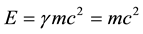 . (5)
. (5)
Now we move to the superstring picture [29] which after decades long debate is commonly perceived as a substantially correct quantum gravity theory. The spacetime of this theory is, as is well known, 10 dimensional and 6 of these dimensions are considered compactified in various ways [28] [29] . Concurrently we can in the meantime view the photon and in fact for the same purpose, the electron to be moving in a space with 137 dimensions equal to the inverse of the electromagnetic fine structure constant which can be shown to be a scali down of the E8E8 dimensions of superstring, i.e. the 496 massless gauge bosons [34] [35] . Seen that way we must scale , i.e. we must scale
, i.e. we must scale  with the intuitively obvious scaling, namely
with the intuitively obvious scaling, namely
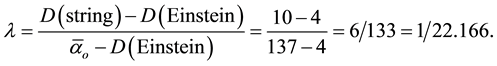 (6)
(6)
i.e. it is approximately 1/22. This is a remarkable result because it means
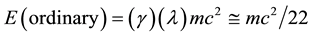 (7)
(7)
which is complete agreement with all known cosmological measurements [30] of the ordinary measureable energy density of the universe. This implies a 95.5 percent dark energy density which being effectively an empty set quantum wave cannot be measured in any ordinary way due to quantum wave collapse [60] . The corresponding formula is
 (8)
(8)
The preceding result and conclusion needs a great deal of further elaboration and refinement. To start with one could find it strange to set  and
and 




In the above equation 









exactly as should be. Having established that 137 is a dimension or particle-like state we should use then the exact E-infinity value which is 




where 


It is clear that the compactification of the 6 dimensions is best dealt with using a Calabi-Yau manifold [16] . This manifold has 6 real dimensions so that 6 can be considered the dimension of this geometrically and topologically remarkable manifold. On the other hand the 





As an aside we mention that at the beginning and due to inaccurate measurements 




The difficulty in the above is that we are involving 'tHooft’s 


We start this time from the bulk E8E8 and note that 




However if we work without super symmetry with Einstein and Kaluza-Klein spacetime [63] , then we have

where 

where we have taken the positive root only as a start. That way we see that 




We recall that the number of states in Witten’s model are given by [28] [29]

Furthermore this model represents a maximally symmetric manifold [28] [29] [44] because

Similarly we know from the Heterotic superstring theory that the number corresponding to 66 in Witten’s model is 63 and that (2)(33) = 126 is exactly the total number of the particle-like states of the standard model. The corresponding number for Witten’s model would consequently be (2)(66) = 132. This is thus the dimension of the modular manifold M6,22 discussed ealier. From the above we see that the scaling factor 


which is the exact integer approximation of cosmic dark energy density and as mentioned repeatedly, is very close to all cosmological measurements and observations while the ordinary cosmic energy density is clearly the ratio of 66 − 63 = 3 to the 66 total which means

as should be [53] - [60] . This last expression is amiable to a simple physical interpretation when Yang-Mills theory and Witten’s model are combined. The number of one and two dimensional Branes making the Witten model is clearly our 66 but there are 4 photons within this expression, namely the classical photon plus the massive photon





as reasoned earlier. Writing 

and

are two results obtained a few years ago [24] [42] [60] within a slightly different scenario. However the surprizing wonder which is not a wonder is that ordinary energy is the position or potential energy of the quantum particle while dark energy is kinetic energy of the quantum wave but both are nothing more or less than the zero set and the empty set of pure mathematics respectively [60] . The problem is incredibly simple when seen as pure mathematics [61] - [63] .
4. Conclusion
By taking internal and external isometries of spacetime carefully into consideration [16] [48] and comparing the standard model of high energy particles with the maximally symmetric spacetime of Witten’s 5-Brane in eleven dimensions, both dark energy and ordinary energy densities of the cosmos were determined [63] . The result agrees completely with previously obtained results as well as actual cosmological measurements and observations [30] . The mathematical basis of the present analysis is rooted in the theoretical structure of E-infinity theory of highly structured rings [12] [13] of which E-infinity theory of high energy physics and loop quantum gravity are in the meantime two well known applications. This was accomplished in part by integrating number theory, the queen of mathematical science and consequently of science in physics [10] . We did this before for mechanics and produced the new and vibrant field of nonlinear dynamics and its associated numerical experiments pioneered by leading researchers such as M. Feigenbaum, M. Berry, the late Russian academician B. Chirikov, the Italian quantum chaos physicist G. Casati and many others [12] . However in the present work we went even one step further by developing a kind of new computational system based on an imaginary Turing-like golden mean computer operating based on a golden mean “binary” system [12] [37] . In view of what we have said in this rather short paper on a vast field, the great paper of Wigner is essentially about the very “reasonable” effectiveness of pure mathematics [60] - [63] .
References
- Weibel, P., Ord, G. and Rössler, O., Eds. (2005) Spacetime Physics and Fractality. Festschrift in Honour of Mohamed El Naschie on the Occasion of His 60th Birthday. Springer, Vienna-New York.
- Yang, C.N. (1987) Square Root of Minus One, Complex Phases and Erwin Schrödinger. In: Kilmister, C.W., Ed., Schrödinger―Centenary Celebration of a Polymath, Cambridge University Press, Cambridge, UK, 53-64.
- Donaldson, S.K. and Kronheimer, P.B. (1990) The Geometry of Four Manifolds. Oxford University Press, Oxford.
- Kodiyalam, V. and Sunder, V.S. (2001) Topological Quantum Field Theories from Subfactors. Chapma & Hall/Crc, London, UK.
- 'tHooft, G. (2005) 50 Years of Yang-Mills Theory. World Scientific, Singapore. http://dx.doi.org/10.1142/5601
- El Naschie, M.S., Rössler, O.E. and Prigogine, I. (1995) Quantum Mechanics, Diffusion and Chaotic Fractals. Pergamon Press/Elsevier, Oxford.
- He, J.-H. (2005) Transfinite Physics. China Scientific and Culture Publishing, Shanghai.
- Sidharth, B.G. and Altaisky, M.V. (2001) Frontiers of Fundamental Physics. Kluwer Academic/Plenum Publishers, New York (see in particular 81-95).
- Friedlander, E. and Grayson, D. (2005) Handbook of K-Theory. Springer, Berlin. http://dx.doi.org/10.1007/978-3-540-27855-9
- Cartier, P., Julia, B., Moussa, P. and Vanhove, P. (2006) Frontiers in Number Theory, Physics and Geometry I. Sprin- ger, Berlin.
- El Naschie, M.S. (2004) A Review of E-Infinity and the Mass Spectrum of High Energy Particle Physics. Chaos, Solitons & Fractals, 19, 209-236. http://dx.doi.org/10.1016/S0960-0779(03)00278-9
- E-Infinity Group: E-Infinity High Energy Communication Nos. 1 to 90. E-Infinity Energyblogspot.com.
- Baker, A. (2013) Close Encounters of the E-Infinity Kind. Journal of Homotopy and Related Structures, 9, 257-282.
- El Naschie, M.S. (1995) Banach-Tarski Theorem and Cantorian Spacetime. Chaos, Solitons & Fractals, 5, 1503-1508. http://dx.doi.org/10.1016/0960-0779(95)00052-6
- El Naschie, M.S. (2011) Quantum Entanglement as a Consequence of a Cantorian Micro Spacetime Geometry. Journal of Quantum Information Science, 1, 50-53. http://dx.doi.org/10.4236/jqis.2011.12007
- Yau, S.-T. (2010) The Shape of Inner Space. Basic Book―Perseus Book Group, New York.
- El Naschie, M.S. (1997) Advanced Prerequisites for E-Infinity Theory. Chaos, Solitons & Fractals, 30, 636-641.
- Argyris, J. and Ciubotariu, C. (1997) On El Naschie’s Complex Time and Gravitation. Chaos, Solitons & Fractals, 8, 743-751. http://dx.doi.org/10.1016/S0960-0779(97)00072-6
- Sigalotti, L. and Mejias, A. (2006) The Golden Ratio in Special Relativity. Chaos, Solitons & Fractals, 30, 521-524. http://dx.doi.org/10.1016/j.chaos.2006.03.005
- El Naschie, M.S. (1994) On Certain “Empty” Cantor Sets and Their Dimensions. Chaos, Solitons & Fractals, 4, 293- 296. http://dx.doi.org/10.1016/0960-0779(94)90152-X
- Crasmareanu, M. and Hretcanu, C. (2008) Golden Differential Geometry. Chaos, Solitons & Fractals, 38, 1229-1238. http://dx.doi.org/10.1016/j.chaos.2008.04.007
- El Naschie, M.S. (1998) Von Neumann Geometry and E-Infinity Quantum Spacetime. Chaos, Solitons & Fractals, 9, 2023-2030.
- El Naschie, M.S. (2007) On the Universality Class of All Universality Classes and E-Infinity Spacetime Physics. Chaos, Solitons & Fractals, 32, 927-936. http://dx.doi.org/10.1016/j.chaos.2006.08.017
- El Naschie, M.S. (2014) Why E Is Not Equal to mc2. Journal of Modern Physics, 5, 743-750. http://dx.doi.org/10.4236/jmp.2014.59084
- El Naschie, M.S. (2008) Average Exceptional Lie Group Hierarchy and High Energy Physics. American Institute of Physics Conference Proceedings, 1018, 15-20.
- He, J.-H., Goldfain, E., Sigalotti, L.D. and Mejias, A. (2006) Beyond the 2006 Physics Nobel Prize for COBE: An Introduction to E-Infinity Spacetime Theory. China Science & Culture Publishing, Shanghai.
- El Naschie, M.S. (2001) On a General Theory for Quantum Gravity. In: Diebner, H., Druckry, T. and Weibel, P., Eds., Science of the Interface, Genista Verlag, Tübingen, 52-57.
- Duff, M. (1999) The World in Eleven Dimensions. IOP Publishing, Bristol.
- Kaku, M. (2000) Strings, Conformal Fields and M-Theory. Springer, New York. http://dx.doi.org/10.1007/978-1-4612-0503-6
- Amendola, L. and Tsujikawa, S. (2010) Dark Energy: Theory and Observations. Cambridge University Press, Cambridge.
- Rindler, W. (2004) Relativity (Special, General and Cosmological). Oxford University Press, Oxford.
- Halvorson, H. (2011) Deep Beauty―Understanding the Quantum World through Mathematical Innovation. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511976971
- Ho, M.-W. (2014) E-Infinity Spacetime, Quantum Paradoxes and Quantum Gravity. Journal of the Institute of Science in Society, 62, 40-43.
- El Naschie, M.S. (1998) Superstrings, Knots and Noncommutative Geometry in E-Infinity Space. International Journal of Theoretical Physics, 37, 2935-2951. http://dx.doi.org/10.1023/A:1026679628582
- El Naschie, M.S. (2006) Elementary Number Theory in Superstring Loop Quantum Mechanics, Twistors and E-Infi- nity High Energy Physics. Chaos, Solitons & Fractals, 27, 297-330. http://dx.doi.org/10.1016/j.chaos.2005.04.116
- El Naschie, M.S. (2004) Quantum Gravity, Clifford Algebra, Fuzzy Set Theory and the Fundamental Constants of Nature. Chaos, Solitons & Fractals, 20, 297-330. http://dx.doi.org/10.1016/j.chaos.2003.09.029
- El Naschie, M.S. (2009) The Theory of Cantorian Spacetime and High Energy Particle Physics (An Informal Review). Chaos, Solitons & Fractals, 41, 2635-2646. http://dx.doi.org/10.1016/j.chaos.2008.09.059
- El Naschie, M.S. (2009) Wild Topology, Hyperbolic Geometry and Fusion Algebra of High Energy Particle Physics. Chaos, Solitons & Fractals, 13, 1935-1945. http://dx.doi.org/10.1016/S0960-0779(01)00242-9
- El Naschie, M.S. (2006) Hilbert, Fock and Cantorian Spaces in the Quantum Two-Slit Gedanken Experiment. Chaos, Solitons & Fractals, 27, 39-42. http://dx.doi.org/10.1016/j.chaos.2005.04.094
- El Naschie, M.S. (1998) Penrose Universe and Cantorian Spacetime as a Model for Noncommutative Quantum Geometry. Chaos, Solitons & Fractals, 9, 931-933. http://dx.doi.org/10.1016/S0960-0779(98)00077-0
- El Naschie, M.S. (2006) On an Eleven Dimensional E-Infinity Fractal Spacetime Theory. International Journal of Nonlinear Sciences & Numerical Simulation, 7, 407-409.
- El Naschie, M.S. (2013) A Resolution of the Cosmic Dark Energy via Quantum Entanglement Relativity Theory. Journal of Quantum Information Science, 3, 23-26. http://dx.doi.org/10.4236/jqis.2013.31006
- El Naschie, M.S. (2006) Topics in the Mathematical Physics of E-Infinity Theory. Chaos, Solitons & Fractals, 30, 656-663. http://dx.doi.org/10.1016/j.chaos.2006.04.043
- El Naschie, M.S. (2007) From Symmetry to Particles. Chaos, Solitons & Fractals, 32, 427-430. http://dx.doi.org/10.1016/j.chaos.2006.09.016
- Nottale, L. (2011) Scale Relativity and Fractal Space-Time. Imperial College Press, London.
- El Naschie, M.S. (1994) Average Symmetry, Stability and Ergodicity of Multidimensional Cantor Sets. Il Nuovo Cimento B Series 11, 2, 149-157. http://dx.doi.org/10.1007/BF02727425
- El Naschie, M.S. (1998) Fredholm Operator and the Wave-Particle Duality. Chaos, Solitons & Fractals, 9, 975-978. http://dx.doi.org/10.1016/S0960-0779(98)00076-9
- El Naschie, M.S. (2008) Symmetry Group Prerequisite for E-Infinity High Energy Physics. Chaos, Solitons & Fractals, 35, 975-978.
- El Naschie, M.S. (2007) Hilbert Space, Poincaré Dodecahedron and Golden Mean Transfiniteness. Chaos, Solitons & Fractals, 31, 787-793. http://dx.doi.org/10.1016/j.chaos.2006.06.003
- Neuenschwander, D. (2011) Emmy Noether’s Wonderful Theorem. The Johns Hopkins University Press, Baltimore.
- Balachandran, A., Kurkcuoglu, S. and Vaidya, S. (2007) Lectures on Fuzzy and Fuzzy SUSY Physics. World Scientific, Singapore.
- Finkelstein, D.R. (1996) Quantum Relativity. A Synthesis of the Ideas of Einstein and Heisenberg. Springer, Berlin.
- El Naschie, M.S. (2014) On a New Elementary Particle from the Disintegration of the Symplectic 'tHooft-Veltman-Wil- son Fractal Spacetime. World Journal of Nuclear Science and Technology, 4, 216-221. http://dx.doi.org/10.4236/wjnst.2014.44027
- El Naschie, M.S. (2014) From Modified Newtonian Gravity to Dark Energy via Quantum Entanglement. Journal of Applied Mathematics and Physics, 2, 803-806.
- Tang, W., Li, Y., Kong, H.Y. and El Naschie, M.S. (2014) From Nonlocal Elasticity to Nonlocal Spacetime and Nanoscience. Bubbfil Nano Technology, 1, 3-12.
- El Naschie, M.S. (2014) Cosmic Dark Energy Density from Classical Mechanics and Seemingly Redundant Riemannian Finitely Many Tensor Components of Einstein’s General Relativity. World Journal of Mechanics, 4, 153-156. http://dx.doi.org/10.4236/wjm.2014.46017
- El Naschie, M.S. (2014) Compactified Dimensions as Produced by Quantum Entanglement, the Four Dimensionality of Einstein’s Smooth Spacetime and 'tHooft’s 4-ε Fractal Spacetime. American Journal of Astronomy & Astrophysics, 2, 34-37.
- Auffray, J.-P. (2014) E-Infinity Dualities, Discontinuous Spacetimes, Xonic Quantum Physics and the Decisive Experiment. Journal of Modern Physics, 5, 1427-1436.
- El Naschie, M.S. (2014) Electromagnetic―Pure Gravity Connection via Hardy’s Quantum Entanglement. Journal of Electromagnetic Analysis and Applications, 6, 233-237.
- El Naschie, M.S. (2013) Topological-Geometrical and Physical Interpretation of the Dark Energy of the Cosmos as a “Halo” Energy of the Schrödinger Quantum Wave. Journal of Modern Physics, 4, 591-596.
- Wigner, E.P. (1960) The Unreasonable Effectiveness of Mathematics in Natural Science. Communications in Pure and Applied Mathematics, 13, 1-14. http://dx.doi.org/10.1002/cpa.3160130102
- Changeux, J. and Connes, A. (1989) Conversation on Mind, Matter and Mathematics. Princeton University Press, Princeton.
- Helal, M.A., Marek-Crnjac, L. and He, J.-H. (2013) The Three Page Guide to the Most Important Results of M. S. El Naschie’s Research in E-Infinity Quantum Physics and Cosmology. Open Journal of Microphysics, 3, 141-145. http://dx.doi.org/10.4236/ojm.2013.34020

