Received 15 January 2015; accepted 16 August 2015; published 19 August 2015

ABSTRACT

In the present paper asymptotic solution of boundary-value problem of three-dimensional micro- polar theory of elasticity with free fields of displacements and rotations is constructed in thin domain of the shell. This boundary-value problem is singularly perturbed with small geometric parameter. Internal iteration process and boundary layers are constructed, problem of their jointing is studied and boundary conditions for each of them are obtained. On the basis of the results of the internal boundary-value problem the asymptotic two-dimensional model of micropolar elastic thin shells is constructed. Further, the qualitative aspects of the asymptotic solution are accepted as hypotheses and on the basis of them general applied theory of micropolar elastic thin shells is constructed. It is shown that both the constructed general applied theory of micropolar elastic thin shells and the classical theory of elastic thin shells with consideration of transverse shear deformations are asymptotically confirmed theories.

Keywords:

Micropolar, Elastic, Thin Shell, Asymptotic Model, Applied Theory

1. Introduction

Current methods of reducing three-dimensional problem of theory of elasticity to two-dimensional problem of theory of plates and shells are the followings: 1) hypotheses method; 2) method of expansion by thickness; 3) asymptotic method [1] -[9] . From recent important papers on construction of micropolar elastic thin plates and shells must be noted papers [10] [11] , where also review of researches is done in the mentioned direction.

The main problem of the general theory of micropolar or classical elastic thin plates and shells is in approximate, but adequate reduction of three-dimensional boundary-value problem of the micropolar or classical theory of elasticity to two-dimensional problem. From our point of view, for achievement of this aim [12] -[14] during the construction of applied theories of thin plates and shells main results of the asymptotic solution of boundary-value or initial boundary-value problem of three-dimensional micropolar or classical theory of elasticity in corresponding thin domains can be used, which are formulated as hypotheses [15] -[18] . Micropolar and classical theories of elastic thin plates and shells, constructed on the basis of such approach, are asymptotically correct theories. This problem is also essential in classical theory of elasticity during the construction of mathematical models of thin plates and shells with the account of transverse shear deformations: in paper [19] it is shown that one of the main theories of plates and shells of Timoshenko’s type, where transverse shear deformations are taken into account, is not asymptotically consistent.

2. Problem Statement

A shell of constant thickness 2h is considered as a three-dimensional elastic body. Equations of the static problem of asymmetric (micropolar, momental) theory of elasticity with free fields of displacements and rotations are the followings [20] [21] :

Equilibrium equations:

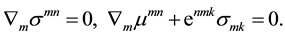(1)

Physical relations:

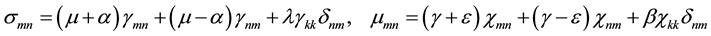. (2)

Geometrical relations:

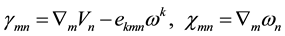. (3)

Here are the components of tensors of force and moment stresses; 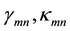are the components of tensors of deformation and bending-torsion; are the components of displacement vector; are the components of free rotation; 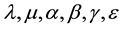are physical constants of the micropolar material of the shell; indices 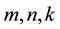take values 1, 2, 3.

It should be noted that if, main equations of the classical theory of elasticity will be obtained from Equations (1)-(3).

We’ll consider three orthogonal system of coordinates (,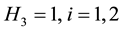), accepted in theory of shells [4] .

Boundary conditions of the first boundary-value problem for front surfaces of the shell are accepted:

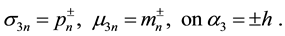(4)

Boundary conditions on the edge 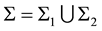of the shell are boundary conditions of the mixed boundary- value problem:

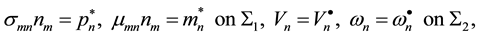(5)

where are the components of the given loads and moments on;, are the given components of displacement and free rotation vectors on.

3. Asymptotic Solution (Construction of Internal Problem) of Boundary-Value Problem of Three-Dimensional Micropolar Theory of Elasticity in Thin Domain of the Shell

It is assumed that the thickness 2h of the shell is small compared with typical radius of curvature of the middle surface of the shell. We’ll proceed from the following basic concept [4] : in the static case general stress-strain state (SSS) of thin shell is composed of internal SSS, covering all three-dimensional shell, and boundary layers, localizing near the surface of the shell edge. On the basis of such approach and results of initial approximation of internal problem the construction of general two-dimensional (asymptotic) model of micropolar thin shells will be possible (in case of also model of elastic shell by classical theory of elasticity).

Question of reduction of three-dimensional static problem of asymmetric theory of elasticity for thin domain of the shell to two-dimensional problem is considered on the basis of asymptotic method with boundary layer [14] , including the question of satisfaction of boundary conditions on shell edge.

At first we’ll consider the construction of internal interactive process. For achievement of this aim we’ll pass to dimensionless coordinates in three-dimensional Equations (1)-(3) of asymmetric theory of elasticity:

(6)

Here quantity characterizes the variability of SSS by coordinates; p, l are integers,; R is the characteristic radius of curvature of the shell middle surface; is the big constant dimensionless geometric parameter, determined with the help of formula. Following dimensionless quantities and dimensionless physical parameters are also considered:

(7)

. (8)

On the basis of (7), (8) following system of dimensionless equations will be obtained instead of system of Equations (1)-(3).

Equilibrium equations:

(9)

Physical-geometrical relations:

(10)

Here

(11)

The case is considered when dimensionless physical parameters (8) have the following values:

(12)

Following replacements of unknown quantities will be done:

(13)

at at

As a result following system of equations will be obtained:

(14)

where

(15)

Following to the asymptotic method, the question is the following: to reduce three-dimensional Equations (14) (with free variables) to two-dimensional ones (with free variables).

Following formulas will be obtained for displacements and rotations, force and moment stresses with asymptotic accuracy on the basis of system (14):

(16)

where

(17)

The aim is to construct asymptotically strictly interactive process for averaged along the shell thickness quantities, which determine the stated problem (i.e. depending only on quantities). From this point of view there is an opportunity to define values from (16) of force stress and moment stress. The approach is the following: at the level of initial approximation of the asymptotic method for quantities and we have:

(18)

Keeping quantities up to order in equilibrium equations and integrating these equations by, we’ll obtain:

(19)

(20)

where and are constants of the integration:

(21)

It must be required that averaged values along the shell thickness of quantities and are equal to zero:

(22)

Substituting (19) and (20) into conditions (22), following formulas will be obtained for and:

Thus for and we’ll obtain:

(23)

(24)

Finally, for quantities and we’ll have the sum of (18), (23), (24):

(25)

(26)

It should be noted that averaged along the shell thickness quantities for and at the level (18) and (25), (26) are equal.

Thus, taking into consideration (25), (26), we’ll have following formulas for displacements, rotations, force and moment stresses instead of (16):

(27)

The constructed asymptotics (27) for internal interaction process of the stated problem gives an opportunity to reduce three-dimensional problem to two-dimensional one (what is already done for displacements, rotations, force and moment stresses). As in the classical theory, instead of components of tensors of force and moment stresses statically equivalent to them integral characteristics are introduced in micropolar theory: forces T_ii, S_ij, N_i3, N_3i, moments M_ii, H_ij, L_ii, L_ij, L_i3, L₃₃ and hypermoments:

(28)

Displacements and rotations of points of the shell middle surface are introduced as follows:

Satisfying boundary conditions (4) on shell surfaces taking into consideration (27), (17), following system of equations of two-dimensional problem of micropolar theory of shells with free fields of displacements and rotations will be obtained:

Equilibrium equations:

(29)

Elasticity relations:

(30)

Geometric relations:

(31)

System of equations of thin shells of classical theory will be obtained from system of Equations (29)-(31) in case of (i.e. system of equations of elastic thin shells of Timoshenko’s type [22] -[25] with some difference).

4. Construction and Studying of Boundary Layers

We’ll proceed from three-dimensional Equations (1)-(3) of micropolar theory of elasticity. It is assumed that the surface of the shell edge, where stress state will be considered, is given with the help of the equation. Replacing of free variables is done on the basis of formulas:

(32)

where quantities have the same meaning as in case of internal problem.

Solution of the obtained system of boundary-value problem must satisfy homogeneous boundary conditions on surfaces of the shell:

(33)

We’ll pass to dimensionless quantities (7), (8) and introduce following notations:

(34)

As a result three-dimensional equations of micropolar theory in dimensionless form will be obtained from Equations (1)-(3) (with consideration of (7), (8)).

At level of asymptotic accuracy boundary layer divides into 4 independent systems of equations:

Force plane problem:

(35)

Force non plane problem:

(36)

Momental plane problem:

(37)

Momental non plane problem:

(38)

where.

The obtained equations of boundary layer in Cartesian coordinates with asymptotic accuracy describe SSS of plain and antiplane force and momental independent problems of micropolar theory of elasticity, taking place in semiband

Requiring that solutions (35)-(38) of boundary layers have fading character when, we’ll obtain that such solutions have following important properties:

(39)

From the above introduced relations (special for micropolar theory of elasticity) following important conclusion can be done: when force and moment stresses are balanced in boundary layer, displacements and free rotations will have the same property.

5. Jointing of Asymptotic Expansions of Internal Interactions Process and Boundary Layer

Considering problem of jointing of internal SSS and boundary layer, following symbolic formula must be introduced for the whole SSS of the shell:

(40)

are called indicators of intensity of plane and antiplane boundary layers. must be chosen so that we can satisfy three-dimensional boundary conditions on shell edge.

Now the first variant of three-dimensional boundary conditions of micropolar theory of elasticity will be considered, when shell edge is loaded with forces and moments. Satisfying boundary conditions, following values will be taken for quantities r and:.

At level boundary conditions on will be as follows:

(41)

where.

Using corresponding conditions from (39) and on the basis of (41), boundary conditions for system (29)-(31) of two-dimensional equations will be obtained:

(42)

Let us study the second variant of three-dimensional boundary conditions of micropolar theory of elasticity, when displacements and rotations are given on the shell edge. Satisfying boundary conditions, following values will be taken for quantities r and in (40):.

At level boundary conditions on will be as follows:

(43)

where.

With the help of conditions from (39) boundary conditions for two-dimensional model will be obtained:

(44)

Mixed three-dimensional boundary conditions are studied, when hinged support takes place.

Following values will be taken for quantities r and in (40):.

At level boundary conditions on will be as follows:

(45)

where

In this case, using conditions from (39), following boundary conditions of hinged-support will be obtained for two-dimensional model:

(46)

6. Asymptotic Model of Micropolar Elastic Thin Shells

Thus two-dimensional theory of micropolar shells is constructed at level of initial approximation of the asymptotic method. System of equations (29)-(31) and boundary conditions (42) (or (43) or (46)) introduce the asymp- totic model of micropolar elastic thin shells with free fields of displacements and rotations.

7. Applied Theory of Micropolar Elastic Thin Shells and Its Justification

Hypotheses method of construction of classical theory of elastic thin shells (i.e. Kirkhov-Love’s or refined hypotheses) has an advantage above the asymptotic method from point of view of engineering, because some simplifications were put in the base of theory, which have physical meaning and also visibility and clarity. Main problem of the construction of applied theory of micropolar elastic thin shells is the following: to formulate such hypotheses that let us reduce three-dimensional problem of micropolar theory of elasticity to adequate two- dimensional boundary-value problem. For achievement of this aim the use of qualitative aspects of asymptotic solution of three-dimensional boundary-value problem (1)-(5) of micropolar theory of elasticity is appropriate in thin domain of the shell.

In papers [12] -[14] the mentioned idea is developed: on the basis of qualitative aspects of asymptotic solution adequate hypotheses are formulated and as a result static and dynamic applied theories of micropolar elastic thin shells and plates are constructed. The accepted hypotheses are the followings:

1) During the deformation initially straight and normal to the shell middle surface fibers rotate freely in space at an angle as a whole rigid body, without changing their length and without remaining perpendicular to the deformed middle surface.

The formulated hypothesis is mathematically written as follows: tangential displacements and normal rotation are distributed in a linear law along the shell thickness:

(47)

Normal displacement and tangential rotations do not depend on coordinate, i.e.

(48)

It should be noted that from the point of view of displacements the accepted hypothesis, in essence, is Timoshenko’s kinematic hypothesis in the classical theory of elastic shells [22] -[25] . Here hypothesis (47), (48) in full we shall call Timoshenko’s generalized kinematic hypothesis in the micropolar theory of shells.

2) In the generalized Hook’s law (2) force stress can be neglected in relation to the force stresses; and analogically, moment stresses can be neglected in relation to the moment stresses.

3) During the determination of deformations, bending-torsions, force and moment stresses, first for the force stresses and moment stress we’ll take:

(49)

After determination of mentioned quantities, values of and will be finally defined by the addition to corresponding values (49) summed up, obtained by integration of the first two and the sixth equilibrium equations from (1), for which the condition will be required, that quantities, averaged along the shells thickness, are equal to zero.

4) Quantities can be neglected in relation to 1.

Now we’ll compare main equations of applied static theory of micropolar elastic thin shells from paper [12] , which are constructed on the basis of above formulated hypotheses, with analogical Equations (29)-(31) of the asymptotic model. It is obvious that equilibrium Equations (29) and geometrical relations (31) are the same. Physical relations from paper [12] differ from physical relations (30) only with underlined terms in relations for It should be noted that underlined terms in relations for and are the result of the fact, that in case of asymptotic theory in relations for quantity is not neglected in relation to. But as it is known such neglect is adopted in theories of thin shells. Analogical explanation has also underlined terms in relations for and. Thus, we can say that the general applied static theory of micropolar elastic thin shells, constructed in paper [12] , is asymptotically correct theory.

Concerning the dynamic theory of micropolar elastic thin shells, it should be noted that the corresponding asymptotic model is constructed in paper [26] , and the applied model, constructed on the basis of the above formulated hypotheses, is introduced in paper [13] . If we compare these two models, we’ll see that motion equations and geometrical relations (which have form (31)) are the same. Concerning physical relations we can say that the difference is underlined terms in relations (30) for.

As in case classical model of elastic thin shells of Timoshenko’s type will be obtained from asymptotic model (Equations (29)-(31)) and also from applied model of paper [12] , we can say that this classical applied refined model of thin shells is the asymptotically correct model (such conclusion can be also done in case of dynamic problem).

It should be noted that in papers [17] [18] applied theories of micropolar elastic thin plates and bars, constructed in papers [14] [27] , are justified on the basis of asymptotic method.

8. Conclusions

In the present paper the question of reduction of three-dimensional boundary-value problem of micropolar and classical theories of elasticity to general applied theories of thin shells is studied. The asymptotics of singularly perturbed boundary-value problem of three-dimensional micropolar theory of elasticity is studied in thin domain of the shell. The internal iteration process and boundary-layers are constructed, jointing of these two iteration processes is studied and boundary conditions are obtained. As a result two-dimensional asymptotic model with free fields of displacements and rotations of micropolar shells is constructed. Transverse shear deformations are automatically taken into consideration in the constructed model. Particularly, classical asymptotic theory of elastic thin shells with consideration of transverse shears can be obtained from the above mentioned micropolar model.

Hypotheses are accepted for the construction of general applied theory of micropolar elastic thin shells. The hypotheses are adequate to the asymptotic behavior of the solution of three-dimensional problem. Such approach ensures the asymptotic exactness of the constructed micropolar and classical theories of thin shells with consideration of transverse shears.

Cite this paper

SamvelSargsyan, (2015) Asymptotically Confirmed Hypotheses Method for the Construction of Micropolar and Classical Theories of Elastic Thin Shells. Advances in Pure Mathematics,05,629-642. doi: 10.4236/apm.2015.510057

References