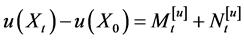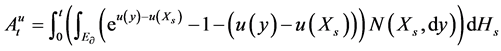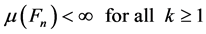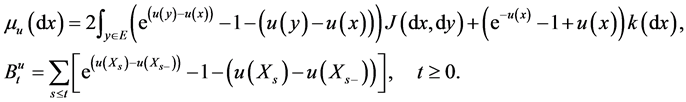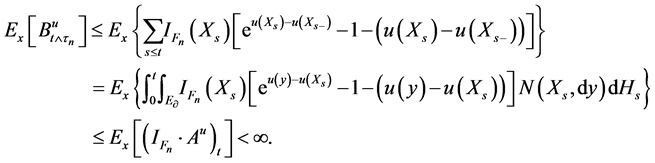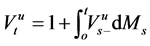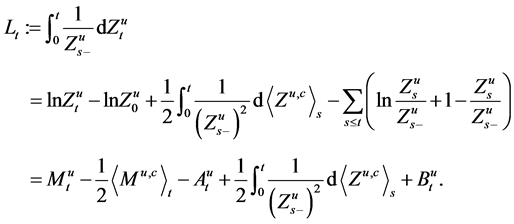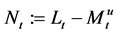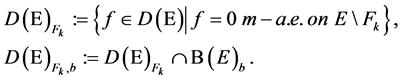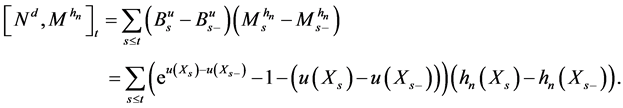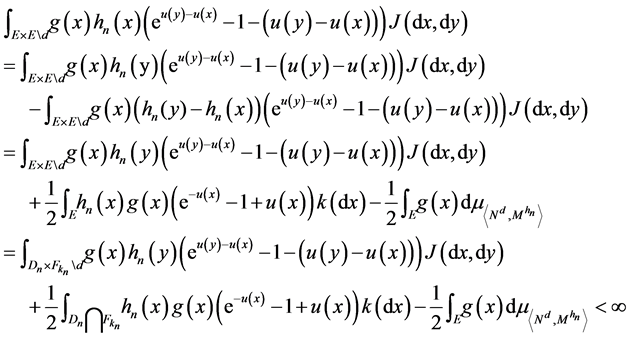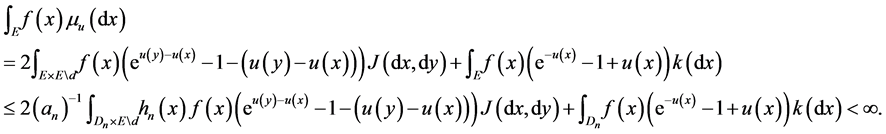Advances in Pure Mathematics
Vol.04 No.10(2014), Article ID:51071,4 pages
10.4236/apm.2014.410063
Necessary and Sufficient Conditions for a Class Positive Local Martingale
Chuanzhong Chen, Saisai Yang
Department of Mathematics, Hainan Normal University, Haikou, China
Email: czchen@hainnu.edu.cn, yangsaisai1989@hotmail.com
Academic Editor: Zechun Hu, Department of Mathematics, Nanjing University, China
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 September 2014; revised 2 October 2014; accepted 13 October 2014
ABSTRACT
Let 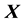 be a Markov process, which is assumed to be associated with a (non-symmetric) Dirichlet form
be a Markov process, which is assumed to be associated with a (non-symmetric) Dirichlet form 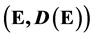 on
on . For
. For , the extended Dirichlet space, we give necessary and sufficient conditions for a multiplicative functional to be a positive local martingale.
, the extended Dirichlet space, we give necessary and sufficient conditions for a multiplicative functional to be a positive local martingale.
Keywords:
Markov Process, Dirichlet Form, Multiplicative Functional, Positive Local Martingale

1. Introduction
Let  be a (non-symmetric) Markov process on a metrizable Lusin space
be a (non-symmetric) Markov process on a metrizable Lusin space  and
and  be a
be a  -finite positive measure on its Borel
-finite positive measure on its Borel 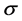 -algebra
-algebra . Suppose that
. Suppose that  is a quasi-regular Dirichlet form on
is a quasi-regular Dirichlet form on  associated with Markov process
associated with Markov process  (we refer the reader to [1] [2] for notations and terminologies of this paper). To simplify notation, we will denote by
(we refer the reader to [1] [2] for notations and terminologies of this paper). To simplify notation, we will denote by 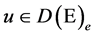 its
its  -quasi- continuous
-quasi- continuous  -version. If
-version. If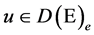
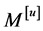
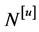
Let 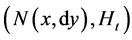

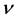
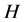
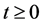
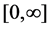
This paper is concerned with the following multiplicative functionals for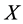
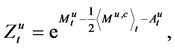
where 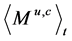

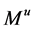
In [3] under the assumption that 
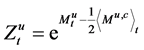
gale and hence a positive supermartingale. In [4] , under the assumption that 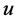
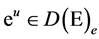



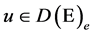
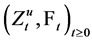
In this paper, we will try to give a complete answer to this question when the Dirichlet forms are non-sym- metric. We present necessary and sufficient conditions for 
2. Main Result
Recall that a positive measure 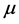
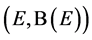
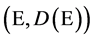
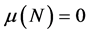
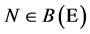
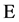

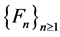
Let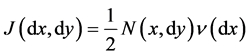
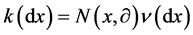
Let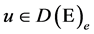
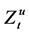
Now we can state the main result of this paper.
Theorem 1 The following are equivalent:
(i) 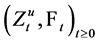
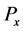
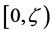

(ii) 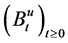

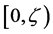
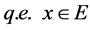
(iii) 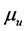

Proof. (iii) 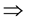
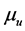
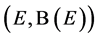

that 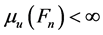
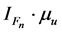

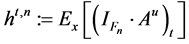
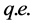
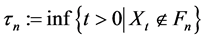
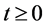
Hence by proposition IV 5.30 of [1] 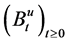
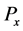
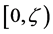
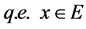
(ii) 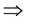
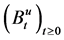
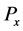
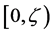
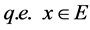

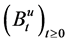
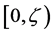
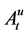
Then 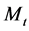
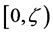
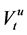
is a local martingale on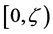

So 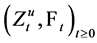
Let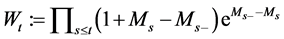
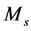
many points at which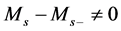
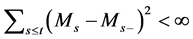
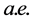
only finitely many points 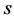
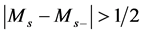
uct. Using the inequality 
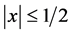
Therefore 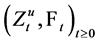
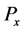
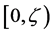
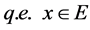
(i) 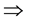
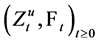

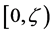
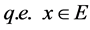
is a local martingale on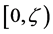
then 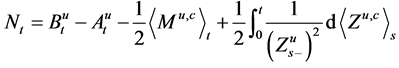
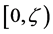
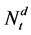
purely discontinuous part of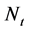
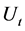
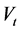
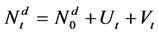
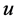
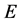
an 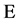
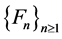
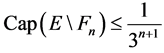
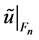
bounded 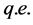

Take a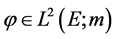

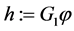
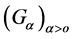


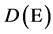

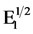
[1] , there exists an 
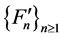
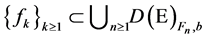
that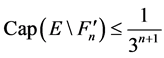
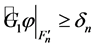
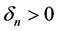

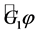
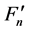
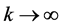
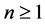
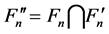
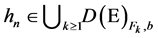
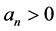
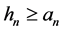
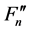
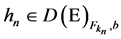
where 
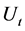
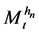
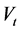
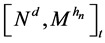
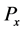

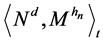
the Revuz measure of 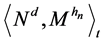
Let 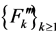
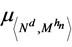
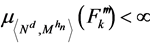
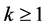
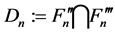
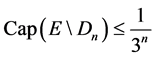
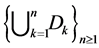

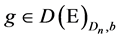
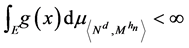
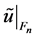
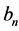
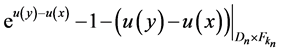
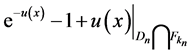
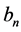
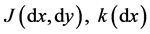
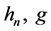
As inequality 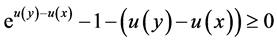
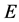
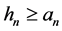

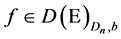
For 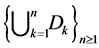
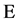
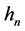
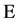

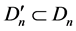
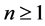
negative 
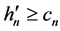
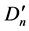
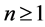
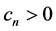
Since
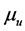
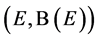
Acknowledgments
We are grateful to the support of NSFC (Grant No. 10961012).
References
- Ma, Z.M. and Rockner, M. (1992) Introduction to Theory of (Non-Symmetric) Dirichlet Forms. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-3-642-77739-4
- Fukushima, M., Oshima, Y. and Takeda, M. (1994) Dirichlet Forms and Symmetric Markov Processes. Walter de Gruyter Berlin, New York. http://dx.doi.org/10.1515/9783110889741
- Chen, C.-Z. and Sun, W. (2009) Girsanov Transformations for Non-symmetric Diffusions. Canadian Journal of Mathematics, 61, 534-547. http://dx.doi.org/10.4153/CJM-2009-028-7
- Chen, Z.-Q. and Zhang, T.-S. (2002) Girsanov and Feynman-Kac Type Transformations for Symmetric Markov Processes. Annales de l’Institut Henri Poincare (B) Probability and Statistics, 38, 475-450. http://dx.doi.org/10.1016/S0246-0203(01)01086-X
- Chen, C.-Z., Ma, Z.-M. and Sun, W. (2007) On Girsanov and Generalized Feynman-Kac Transformations for Symmetric Markov Process. World Scientific, 10, 141-163.
- Oshima. Y. (2013) Semi-Dirichlet Forms and Markov Processes. Walter de Gruyter, Berlin. http://dx.doi.org/10.1515/9783110302066
- He, S.W., Wang, J.G. and Yan, J.A. (1992) Semimartingale Theory and Stochastic Calculus. Science Press, Beijing.
- Kallsen, J. and Shiryaev, A.N. (2002) The Cumulant Process and Esscher’s Change of Measure. Finance Stochast, 6, 397-428. http://dx.doi.org/10.1007/s007800200069