Advances in Pure Mathematics
Vol.04 No.09(2014), Article ID:49912,4 pages
10.4236/apm.2014.49058
On the Initial Subalgebra of a Graded Lie Algebra
Thomas B. Gregory
Department of Mathematics, The Ohio State University at Mansfield, Mansfield, Ohio, USA
Email: gregory.6@osu.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 July 2014; revised 11 August 2014; accepted 21 August 2014
ABSTRACT
We show that each irreducible, transitive finite-dimensional graded Lie algebra over a field of prime characteristic p contains an initial subalgebra in which the pth power of the adjoint transformation associated with any element in the lowest gradation space is zero.
Keywords:
Prime-Characteristic Lie Algebras

1. Introduction
In the classification of the simple finite-dimensional Lie algebras over fields of prime characteristic, irreducible transitive finite dimensional graded Lie algebras play a fundamental role [1] . The simple finite dimensional Lie algebras over algebraically closed fields of characteristic greater than three have been classified [2] . Work is being done in characteristic three [3] - [7] . It is well known that in Lie algebras of Cartan type, there is a (not necessarily proper) subalgebra, the “initial piece,” which contains the sum of the negative gradations spaces of the Lie algebra, and in which the 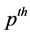 power of the adjoint representation associated with any element of the lowest gradation space is zero. In this paper, we prove that any irreducible, transitive finite-dimensional graded Lie algebra contains such an initial subalgebra. Indeed, we prove the following theorem.
power of the adjoint representation associated with any element of the lowest gradation space is zero. In this paper, we prove that any irreducible, transitive finite-dimensional graded Lie algebra contains such an initial subalgebra. Indeed, we prove the following theorem.
2. Main Theorem
Let
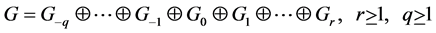
be an irreducible, transitive, finite-dimensional graded Lie algebra over a field of characteristic 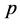 such that M(G) = 0 [8] . Then
such that M(G) = 0 [8] . Then  contains an irreducible, transitive depth-
contains an irreducible, transitive depth-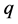 graded subalgebra
graded subalgebra
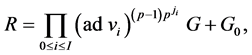
where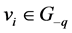 , and where I is a non-negative whole number. We have
, and where I is a non-negative whole number. We have ,
,  , and
, and  for all
for all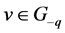 .
.
If , then the conclusion of the theorem obviously holds. In what follows, therefore, we will assume that
, then the conclusion of the theorem obviously holds. In what follows, therefore, we will assume that .
.
2. Intermediate Results
To prove the Main Theorem, we will make use of the following series of lemmas, in which we assume the hypotheses and notation of the Main Theorem. We note that by, for example, [9] (Lemma 6), 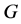 is transitive in its negative part. (Note that the lemmas we quote from [9] are valid for all prime characteristics.) As usual, we assume throughout that M(G) = 0 [8] .
is transitive in its negative part. (Note that the lemmas we quote from [9] are valid for all prime characteristics.) As usual, we assume throughout that M(G) = 0 [8] .
Lemma 1. If M is an abelian 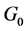 -submodule of G, then for any
-submodule of G, then for any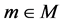 ,
, 


Proof. For any


so that modulo
Lemma 2. If 




Proof. As in the proof of Lemma 1 above, we have, for any 


Lemma 3. If



Proof. Let 



since, as we have seen in the proofs of the previous lemmas, 




subalgebra, as required.
Lemma 4. Let I be the minimal (graded) ideal of G [8] . If 

integers j and k, with 




Proof. Suppose




so 

Lemma 5. If 



Proof. We will show that 







so 


and



by, for example, [9] (Lemma 9), 


(by Lemma 4, as we noted earlier in the proof). But then, since
so 
have 

Lemma 6. If 




zero, and
Proof. If


trary to hypothesis. By Lemma 5, 
is a 

Since 


Thus, both 

Lemma 7. Let 




Proof. Suppose

Thus









lator of 




is irreducible as a 
i.e., 

again 


Lemma 8. Let 









Proof. For 


so


closure under addition being obvious. Note that we must have
have
By Lemma 6,


Thus, by transitivity and irreducibility,
Consequently, we conclude that


also. Thus, 


clude that 
more times, we conclude the proof of Lemma 8.
3. Proof of Main Theorem
Let 










is an irreducible, transitive, finite-dimensional depth-


is an irreducible, transitive, finite-dimensional depth-q graded Lie algebra to which we may apply Lemma 8 again. Since 
Consequently, if










Since the sequence 


If, in the above argument, we replace 













Remark. Note that if we define




References
- Kostrikin, A.I. and Shafarevich, I.R. (1969) Graded Lie Algebras of Finite Growth. Mathematics of the USSR-Izvestiya, 3, 237-304. (English)
- Premet, A. and Strade, H. (2006) Classification of Finite-Dimensional Simple Lie Algebras in Prime Characteristics. arXiv: math/0601380v2 [math. RA].
- Skryabin, S.M. (1992) New Series of Simple Lie Algebras of Characteristic 3. Russian Academy of Sciences Sbornik Mathematics, 70, 389-406. (English)
- Benkart, G.M., Kostrikin, A.I. and Kuznetsov, M.I. (1996) The Simple Graded Lie Algebras of Characteristic Three with Classical Reductive Component L0. Communications in Algebra, 24, 223-234. http://dx.doi.org/10.1080/00927879608825563
- Benkart, G.M., Gregory, T.B. and Kuznetsov, M.I. (1998) On Graded Lie Algebras of Characteristic Three with Classical Reductive Null Component. In: Ferrar, J.C. and Harada, K., Eds., The Monsteer and Lie Algebras, Vol. 7, Ohio State University Mathematical Research Publications, 149-164.
- Gregory, T.B. and Kuznetsov, M.I. (2004) On Depth-Three Graded Lie Algebras of Characteristic Three with Classical Reductive Null Component. Communications in Algebra, 32, 3339-3371. http://dx.doi.org/10.1081/AGB-120039401
- Gregory, T.B. and Kuznetsov, M.I. On Graded Lie Algebras of Characteristic Three with Classical Reductive Null Component. (In Preparation)
- Weisfeiler, B.J. (1978) On the Structure of the Minimal Ideal of Some Graded Lie Algebras in Characteristic p > 0. Journal of Algebra, 53, 344-361. http://dx.doi.org/10.1016/0021-8693(78)90280-6
- Benkart, G.M. and Gregory, T.B. (1989) Graded Lie Algebras with Classical Reductive Null Component. Mathematische Annalen, 285, 85-98. http://wdx.doi.org/10.1007/BF01442673
- Jacobson, N. (1962) Lie Algebras, Tracts in Mathematics. Vol. 10, Interscience, New York.































