Advances in Pure Mathematics
Vol.4 No.7(2014), Article
ID:48174,7
pages
DOI:10.4236/apm.2014.47042
Convergence Theorems for k-Strictly Pseudononspreading Multivalued in Hilbert Spaces
Hongbo Liu*, Yi Li
School of Science, Southwest University of Science and Technology, Mianyang, China
Email: *liuhongbo@swust.edu.cn
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 May 2014; revised 15 June 2014; accepted 30 June 2014
Abstract
We introduce a k-strictly pseudononspreading multivalued in Hilbert spaces more general than the class of nonspreading multivalued. We establish some weak convergence theorems of the sequences generated by our iterative process. Some new iterative sequences for finding a common element of the set of solutions for equilibrium problem was introduced. The results improve and extend the corresponding results of Osilike Isiogugu [1] (Nonlinear Anal.74 (2011)) and others.
Keywords:Equilibrium Problem, K-Strictly Pseudononspreading Multivalued Mapping, Common Fixed Point

1. Introduction
Throughout this paper, we denote by ![]() and
and  the sets of positive integers and real numbers, respectively. Let
the sets of positive integers and real numbers, respectively. Let ![]() be a nonempty closed subset of a real Hilbert space
be a nonempty closed subset of a real Hilbert space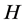 . Let
. Let  and
and 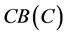 denote the family of nonempty subsets and nonempty closed bounded subsets of
denote the family of nonempty subsets and nonempty closed bounded subsets of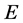 , respectively. The Hausdorff metric on
, respectively. The Hausdorff metric on  is defined by
is defined by

for , where
, where . An element
. An element ![]() is called a fixed point of a multivalued mapping
is called a fixed point of a multivalued mapping 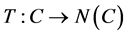 if
if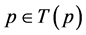 . The set of fixed points of a multivalued mapping
. The set of fixed points of a multivalued mapping 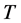 is represented by
is represented by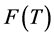 .
.
The multivalued mapping 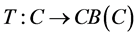 is called nonexpansive if
is called nonexpansive if
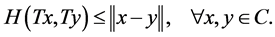
The multivalued mapping 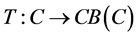 is called quasi-nonexpansive if
is called quasi-nonexpansive if 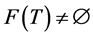 and
and
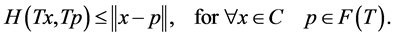
Iterative process for approximating fixed points (and common fixed points) of nonexpansive multivalued mappings have been investigated by various authors (see [2] -[5] ).
Recently, Kohsaka and Takahashi (see [6] [7] ) introduced an important class of mappings which they called the class of nonspreading mappings. Let ![]() be a subset of Hilbert space
be a subset of Hilbert space , they called a mapping
, they called a mapping ![]() nonspreading if
nonspreading if
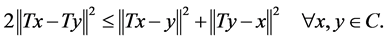
Lemoto and Takahashi [8] proved that ![]() is nonspreading if and only if
is nonspreading if and only if
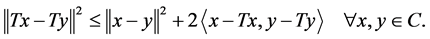
Now, inspired by [6] and [7] , we propose a definition as follows.
Definition 1.1 The multivalued mapping  is called nonspreading if
is called nonspreading if
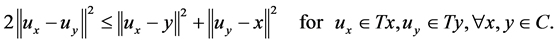 (1.1)
(1.1)
By Takahashi [8] , We get also the multivalued mapping  is nonspreading if and only if
is nonspreading if and only if
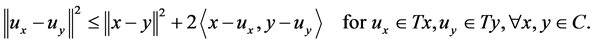 (1.2)
(1.2)
Infact,

Definition 1.2 The multivalued mapping 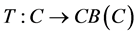 is called
is called 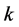 -strictly pseudononspreading if there exists
-strictly pseudononspreading if there exists  such that
such that
 (1.3)
(1.3)
Observe that suppose  is k-strictly pseudononspreading with
is k-strictly pseudononspreading with , and
, and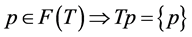 , then
, then

Clearly every nonspreading multivalued mapping is k-strictly pseudononspreading multivalued mapping. The following example shows that the class of k-strictly pseudononspreading mappings is more general than the class of nonspreading mappings.
Example (see [1] page 1816 Example 1), Let 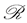 denote the reals with the usual norm. Let
denote the reals with the usual norm. Let  be defined for each
be defined for each  by
by
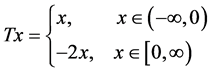
The equilibrium problem for ![]() is to find
is to find 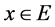 such that
such that ,
, . The set of such solution is denoted by
. The set of such solution is denoted by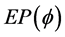 . Given a mapping
. Given a mapping , let
, let 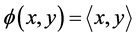 for all
for all![]() . The
. The 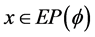 if and only if
if and only if 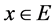 is a solution of the variational inequality
is a solution of the variational inequality  for all
for all![]() .
.
Numerous problems in physics, optimization, and economics can be reduced to find a solution of the equilibrium problem. Some methods have been proposed to solve the equilibrium problem see, for instance, Blum and Oettli [9] , Combettes and Hirstoaga [10] , Li and Li [11] , Giannessi, Maugeri, and Pardalos [12] , Moudafi and Thera [13] and Pardalos, Rassias and Khan [14] , Ceng et al. [15] . In the recent years, the problem of finding a common element of the set of solutions of equilibrium problems and the set of fixed points of single-valued nonexpansive mappings in the framework of Hilbert spaces has been intensively studied by many authors.
In this paper, inspired by [1] we propose an iterative process for finding a common element of the set of solutions of equilibrium problem and the set of common fixed points of k-strictly pseudononspreading multivalued mapping in the setting of real Hilbert spaces. We also prove the strong and weak convergence of the sequences generated by our iterative process. The results presented in the paper improve and extend the corresponding results in [1] and others.
2. Preliminaries and Lemma
In the sequel, we begin by recalling some preliminaries and lemmas which will be used in the proof.
Lemma 2.1 Let  be a real Hilbert space, for all
be a real Hilbert space, for all ![]() and
and , then the following well known results hold:
, then the following well known results hold:
(i) 
(ii) 
(iii) If 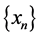 is a sequence in
is a sequence in  which converges weakly to
which converges weakly to  then
then
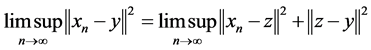
Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space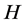 . The nearest point projection
. The nearest point projection  defined from
defined from 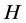 onto
onto ![]() is the function which assigns to each
is the function which assigns to each 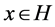 its nearest point denoted by
its nearest point denoted by  in
in![]() . Thus
. Thus 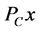 is the unique point in
is the unique point in ![]() such that
such that
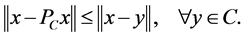
It is known that for each ![]()

Lemma 2.2 (see [5] ) Let ![]() be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space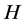 . Let
. Let  be the metric projection of
be the metric projection of 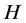 onto
onto![]() . Let
. Let  be a sequence in
be a sequence in ![]() and let
and let 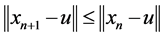 for all
for all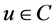 . Then
. Then 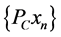 converges strongly.
converges strongly.
We present the following properties of a k-strictly pseudononspreading multivalued mapping.
Lemma 2.3 Let 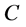 be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space , and let
, and let 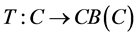 be a k-strictly pseudononspreading multivalued mapping. If
be a k-strictly pseudononspreading multivalued mapping. If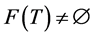 , and
, and , then it is closed and convex.
, then it is closed and convex.
Proof. Let 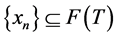 and
and 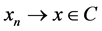 (as
(as ). Since
). Since 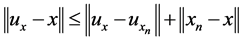 and
and
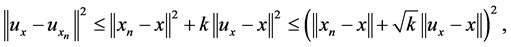
we have 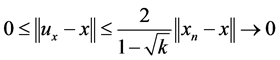 (as
(as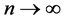 ). Hence
). Hence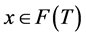 .
.
Next let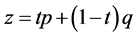 , where
, where 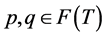 and
and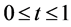 , we have
, we have
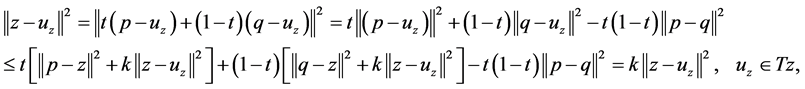
Thus  and hence
and hence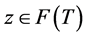 . This complete the proof of Lemma 2.3 Lemma 2.4 Let
. This complete the proof of Lemma 2.3 Lemma 2.4 Let ![]() be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space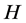 , and let
, and let  be a k-strictly pseudononspreading multivalued mapping. If
be a k-strictly pseudononspreading multivalued mapping. If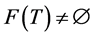 , and
, and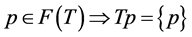 , then
, then  is demiclosed at 0.
is demiclosed at 0.
Proof. Let 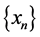 be a sequence in
be a sequence in ![]() which
which 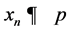 and
and 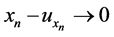 (as
(as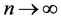 ).
).
Since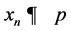 , it is bounded. For each
, it is bounded. For each 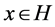 define
define 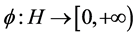 by
by
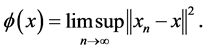
Then from Lemma 2.1 we obtain
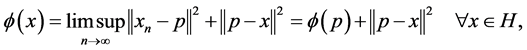
and so  (where
(where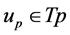 ).
).
In addition,

We obtain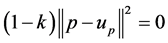 . Thus
. Thus  and hence
and hence . This complete the proof of Lemma 2.4. ,
. This complete the proof of Lemma 2.4. ,
3. Main Results
Theorem 3.1 Let  be a nonempty closed convex subset of a real Hilbert space
be a nonempty closed convex subset of a real Hilbert space , and let
, and let 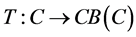 be a k-strictly pseudononspreading multivalued mapping with
be a k-strictly pseudononspreading multivalued mapping with 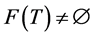 and
and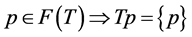 . Let
. Let  and
and 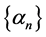 be a real sequence in
be a real sequence in  such that
such that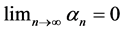 . Let
. Let  and
and 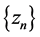 be sequences generated initially by an arbitrary element
be sequences generated initially by an arbitrary element 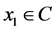 and then by
and then by
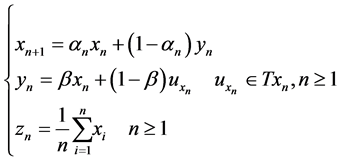
Then, the sequences 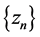 converge weakly to
converge weakly to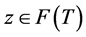 , where
, where 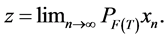
Proof. Let 
First, We claim that .
.
Indeed, if , then
, then
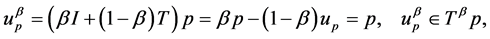
this implies 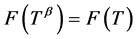 and
and 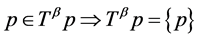 Next, for
Next, for ![]() we have
we have
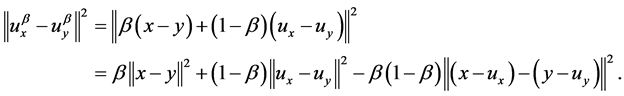 (3.1)
(3.1)
By (1.3) and (3.1), we obtain
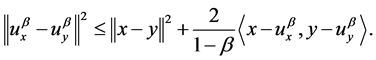 (3.2)
(3.2)
Observe also that for each 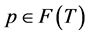
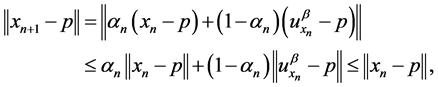
hence  is bounded. By Lemma 2.1 and (3.2), we obtain
is bounded. By Lemma 2.1 and (3.2), we obtain
 (3.3)
(3.3)
Since
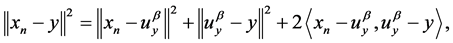 (3.4)
(3.4)
it follows from (3.3) and (3.4) that
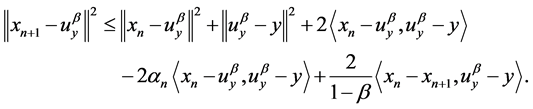 (3.5)
(3.5)
Summing (3.5) from n = 1 to n, and dividing by n we obtain
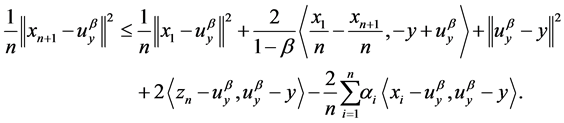 (3.6)
(3.6)
Since 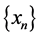 is bounded,then
is bounded,then 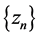 is also bounded. Thus there exists a subsequence
is also bounded. Thus there exists a subsequence  of
of 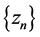 such that
such that 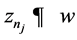 (as
(as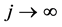 ). we also have
). we also have
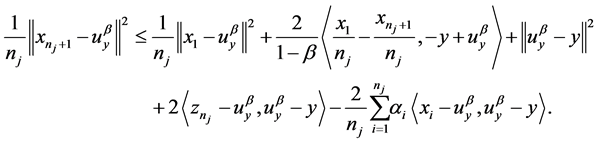 (3.7)
(3.7)
As  we obtain from (3.7) that
we obtain from (3.7) that
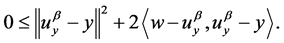 (3.8)
(3.8)
Since ![]() was arbitrary, setting
was arbitrary, setting 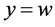 in (3.8) we have
in (3.8) we have

from which it follows that . Since
. Since 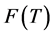 is closed and convex by Lemma 2.3, thus we can define the projection
is closed and convex by Lemma 2.3, thus we can define the projection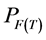 .
.
From Lemma 2.2, 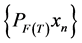 converges strongly. Let
converges strongly. Let .
.
Next we show that .
.
Since  and
and 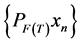 are bounded, there exists
are bounded, there exists ![]() such that
such that 
 , then we obtain by
, then we obtain by 
 (3.9)
(3.9)
Summing (3.9) from ![]() to
to![]() , and dividing by
, and dividing by ![]() we obtain
we obtain
 (3.10)
(3.10)
Sine 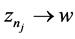 as
as![]() , and
, and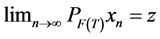 , we have
, we have
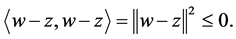
Hence![]() , so, the sequences
, so, the sequences  converge weakly to
converge weakly to , where
, where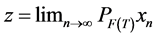 . This complete the proof of Theorem 3.1. ,
. This complete the proof of Theorem 3.1. ,
Acknowledgments
This work is supported by the Doctoral Program Research Foundation of Southwest University of Science and Technology (No.11zx7129) and the National Natural Science Foundation of China (No.71071102).
The authors are very grateful to the referees for their helpful comments and valuable suggestions.
References
- Osilike, M.O. and Isiogugu, F.O. (2011) Weak and Strong Convergence Theorems for Nonspreading-Type Mappings in Hilbert Spaces. Nonlinear Analysis: Theory, Methods & Applications, 74, 1814-1822. http://dx.doi.org/10.1016/j.na.2010.10.054
- Song, Y. and Wang, H. (2009) Convergence of Iterative Algorithms for Multivalued Mappings in Banach Spaces. Nonlinear Analysis, 70, 1547-1556. http://dx.doi.org/10.1016/j.na.2008.02.034
- Shahzad, N. and Zegeye, H. (2009) On Mann and Ishikawa Iteration Schemes for Multivalued Maps in Banach Space. Nonlinear Analysis, 71, 838-844. http://dx.doi.org/10.1016/j.na.2008.10.112
- Eslamian, M. and Abkar, A. (2011) One-Step Iterative Process for a Finite Family of Multivalued Mappings. Mathematical and Computer Modelling, 54, 105-111. http://dx.doi.org/10.1016/j.mcm.2011.01.040
- Takahashi, W. and Toyoda, M. (2003) Weak Convergence Theorems for Nonexpansive Mappings and Monotone Mappings. Journal of Optimization Theory and Applications, 118, 417-428. http://dx.doi.org/10.1023/A:1025407607560
- Kohsaka, F. and Takahashi, W. (2008) Fixed Point Theorems for a Class of Nonlinear Mappings Relate to Maximal Monotone Operators in Banach Spaces. Archiv der Mathematik (Basel), 91, 166-177. http://dx.doi.org/10.1007/s00013-008-2545-8
- Kohsaka, F. and Takahashi, W. (2008) Existence and Approximation of Fixed Points of Firmly Nonexpansive-Type Mappings in Banach Spaces. SIAM Journal on Optimization, 19, 824-835. http://dx.doi.org/10.1137/070688717
- Iemoto, S. and Takahashi, W. (2009) Approximating Commom Fixed Points of Nonexpansive Mappings and Nonspreading Mappings in a Hilbert Space. Nonlinear Analysis, 71, 2082-2089. http://dx.doi.org/10.1016/j.na.2009.03.064
- Blum, E. and Oettli, W. (1994) From Optimization and Variational Inequalities to Equilibrium Problems. The Mathematics Student, 63, 123-145.
- Combettes, P.L. and Hirstoaga, S.A. (2005) Equilibrium Programming in Hilbert Spaces. Journal of Nonlinear and Convex Analysis, 6, 117-136.
- Li, X.B. and Li, S.J. (2010) Existence of Solutions for Generalized Vector Quasi-Equilibrium Problems. Optimization Letters, 4, 17-28. http://dx.doi.org/10.1007/s11590-009-0142-9
- Giannessi, F., Maugeri, G. and Pardalos, P.M. (2001) Equilibrium Problems: Nonsmooth Optimization and Variational Inequality Models. Kluwer Academics Publishers, Dordrecht.
- Moudafi, A. and Thera, M. (1999) Proximal and Dynamical Approaches to Equilibrium Problems, In: Lecture Note in Economics and Mathematical Systems, Vol. 477, Springer-Verlag, New York, 187-201.
- Pardalos, P.M., Rassias, T.M. and Khan, A.A. (2010) Nonlinear Analysis and Variational Problems. Springer, Berlin. http://dx.doi.org/10.1007/978-1-4419-0158-3
- Ceng, L.C., Al-Homidan, S., Ansari, Q.H. and Yao, J.C. (2009) An Iterative Scheme for Equilibrium Problems and Fixed Point Problems of Strict Pseudo-Contraction Mappings. Journal of Computational and Applied Mathematics, 223, 967-974. http://dx.doi.org/10.1016/j.cam.2008.03.032
NOTES

*Corresponding author.

