Advances in Pure Mathematics
Vol.04 No.06(2014), Article ID:46624,1 pages
10.4236/apm.2014.46032
A Note on the Height of Transitive Depth-One Graded Lie Algebras Generated by Their Local Parts
Thomas B. Gregory
Department of Mathematics, The Ohio State University at Mansfield, Mansfield, USA
Email: gregory.6@osu.edu
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 March 2014; revised 28 April 2014; accepted 6 May 2014
ABSTRACT
For a transitive depth-one graded Lie algebra over a field of characteristic greater than two, a limit on the degree of the highest gradation space is determined.
Keywords:
Graded Lie Algebras

Let the characteristic 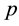 of the base field be greater than two. In [1] , V.G. Kac defined the local part of a graded Lie algebra
of the base field be greater than two. In [1] , V.G. Kac defined the local part of a graded Lie algebra  to be
to be  which we will assume to be finite dimen- sional. We will refer to
which we will assume to be finite dimen- sional. We will refer to 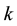 as the height of
as the height of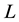 .
.
Lemma 1. If 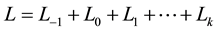 is a transitive graded Lie algebra which is generated by its finite- dimensional local part, then the height
is a transitive graded Lie algebra which is generated by its finite- dimensional local part, then the height  of
of 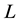 is less than or equal to
is less than or equal to , where
, where 
Proof. If 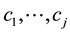 are any elements of
are any elements of 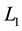 (or
(or 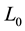 or
or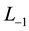 , respectively) and
, respectively) and 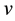 is an element of
is an element of 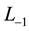 then we have by the Leibniz rule that
then we have by the Leibniz rule that
Now, 











Note that the height of the Jacobson-Witt algebra 

Because the gradation spaces of positive degree of transitive graded Lie algebras are contained in Cartan prolongations, those gradation spaces will be finite dimensional whenever the local part of the transitive Lie algebra is finite dimensional. Thus, when the gradation degrees of a transitive graded Lie algebra with a finite- dimensional local part are bounded, the Lie algebra is itself finite dimensional.
References
- Kac, V.G. (1968) Simple Irreducible Graded Lie Algebras of Finite Growth. Mathematics of the USSR-Izvestiya, 2, 1271-1312 (English), Izvestiya Akademii Nauk SSSR. Seriya Matematicheskaya, 32, 1323-1367 (Russian).



