Received 28 February 2014; revised 28 March 2014; accepted 6 April 2014

ABSTRACT

For 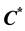-algebras 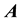and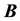, the constant involved in the canonical embedding of 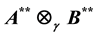into 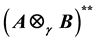is shown to be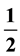. We also consider the corresponding operator space version of this embedding. Ideal structure of 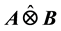is obtained in case 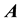or 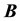has only finitely many closed ideals.

Keywords:

Banach Space Projective Tensor Norm, Operator Space Projective Tensor Norm

1. Introduction

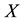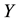The systematic study of various tensor norms on the tensor product of Banach spaces was begun with the work of Schatten [1] , which was later studied by Grothendieck in the context of locally convex topological space. One of the most natural and useful tensor norm is the Banach space projective tensor norm. For a pair of arbitrary Banach spaces and and 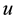an element in the algebraic tensor product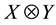, the Banach space projective tensor norm is defined to be

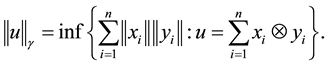
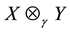will denote the completion of 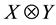with respect to this norm. For operator spaces and, the operator space projective tensor product of and is denoted by and is defined to be the completion of with respect to the norm:

the infimum taken over and all the ways to write, where, ,

and

and

.

Kumar and Sinclair defined an embedding from into, and using the non-com- mutative version of Grothendieck’s theorem to the setting of bounded bilinear forms on -algebras, it was

shown that this embedding satisfies ([2] , Theorem 5.1). Recently, analogue of Grothen-

dieck’s theorem for jointly completely bounded (jcb) bilinear forms was obtained by Haagerup and Musat [3] . Using this form for jcb, the canonical embedding for the operator space projective tensor product have been

studied by Jain and Kumar [4] , and they showed that the embedding from into satisfies.

In Section 2, an alternate approach for the bi-continuity of the canonical embedding of into has been presented with an improved constant. Our proof essentially uses the fact that the dual of the Banach space projective tensor norm is the Banach space injective tensor norm. We also consider the corresponding operator space version of this embedding and discuss its isomorphism. As a consequence, one can obtain the equivalence between the Haagerup tensor norm and the Banach space projective tensor norm (resp. operator space projective tensor norm).

In the next section, it is shown that if the number of all closed ideals in one of the -algebras is finite then every closed ideal of is a finite sum of product ideals. One can obtain all the closed ideals of as, and, and the closed

ideals of as, where or,

for each, for an infinite dimensional separable Hilbert space and locally compact Hausdorff topological space. Similarly, the closed ideal structure of, where is any -algebra and is the multiplier algebra of, being a nonunital, non-element- ary, separable, simple AF -algebra, can be obtained. We may point that such result fails for, the minimal tensor product of -algebras and.

Section 4 is devoted to the inner automorphisms of and for -algebras as well as for operator algebras. Recall that the Haagerup norm on the algebraic tensor product of two operator spaces and is defined, for, by

where infimum is taken over all the ways to write

where. The Haagerup tensor product is defined to be the comple-

tion of in the norm [5] .

2. Isomorphism of Embeddings

For Banach spaces and and, , define a linear map as

, for and. Using ([6] , Proposition 1.2), it is easy to see that

is well defined. Also, clearly this map is linear and contractive with respect to, and in fact, and hence can be extended to with. A bilinear form in is called nuclear if

, and the nuclear norm of is defined to be. The

Banach space of nuclear bilinear forms is denoted by. For -algebras and, consider the canonical map from into, the dual of the Banach space injective tensor product of and, defined by

where is the natural isometry of into, is as above with and, is the natural inclusion of into, the space of integral bilinear forms.

Lemma 2.1 For -algebras and, the canonical map the space of integral operators from to satisfies for all. In par-

ticular, is bi-continuous.

Proof: The inequality of the right hand side follows directly from the definition of. Let and. By the Hahn Banach Theorem, there exists with such that.

Since, so, for some, for all and with. By ([7] , Proposition 2.1(2)), there is a net of finite rank operators from to such that and for any.

Now, for each, corresponding to we can associate. For, there is such that for all. Thus. Since is a finite rank operator, so let. Choose an Auerbach basis for with associated coordinate functionals in. Thus, for any, , for.

By using, it follows that, for. Therefore, for any and,

where is the canonical isometric map from to. Thus and so

. Moreover, for, we have

Since is arbitrary, so.

Next, we consider the map defined by.

Proposition 2.2 For -algebras and, the natural map is bi-conti-

nuous and, for all.

Proof: By the above lemma, we have a map with for all

. Also, ([6] , Proposition 3.21) shows that the natural inclusion map is isometric. We will show that. For, , and,

,

since for. Thus

. Therefore, by linearity and continuity, , and hence the map satisfies for all.

Haagerup proved that every bounded bilinear form on can be extended uniquely to a separately normal norm preserving bounded bilinear form on ([7] , Corollary 2.4), so we have a continuous iso-

metric map. Set

where is the natural embedding of into. Kumar and Sinclair proved that this

embedding is a bi-continuous map with lower bound ([2] , Theorem 5.1). We re-establish its bi-continuity

with an alternate proof and an improved lower bound.

Theorem 2.3 For -algebras and, the natural embedding satisfies for all.

Proof: We know that the natural embedding is isometric. Thus, by

the Hahn Banach theorem, is a quotient map. We will show that

where is as in Proposition 2.2. Since and are linear and continuous, it suffices to show that and agree on. Note that, for, , and,

where is the bilinear form corresponding to.

Since and so, by Goldstine’s Lemma, there are nets and such that converges to in and converges to in. The separate -continuity of the

bilinear form and the equality shows that . Thus,. Hence, by Proposition 2.2, we deduce that .

Remark 2.4 (i) Note that, for a -algebra having Completely positive approximation property, the canonical embedding of into is isometric by ([8] , Theorem 3.6) and ([9] , Theorem 3.6). However, for the largest Banach space tensor norm, the embedding is isometic if one of the -algebra has the metric approximation property, which follows directly by using ([6] , Theorem 4.14) in the above theorem.

(ii) For a locally compact Hausdorff topological group, let and be the group - algebra and the reduced group -algebra of, respectively. Then, for any -algebra and a discrete

amenable group, the natural embedding of into is isometric by ([8] , Theorem 4.2); and for any amenable group, the natural embedding of into

is isometric by ([8] , Proposition 4.1).

(iii) The natural embedding is isomorphism if has the approximation property, has the Radon Nikodym property and every bilinear form on is nuclear. This follows directly by observing that if has the Radon Nikodym property then ([6] , Theorem 5.32) gives us

where and denote the Pietsch integral and nuclear operators from to, respectively [6] . Clearly, bijectivity follows if we show that is an onto map. For this, let so it is nuclear. Since has the approximation property, so there exists an element such that

where is an isometric isomorphism from to ([6] , Corollary 4.8). Consider the canonical map. Of course on, and hence by linearity and con- tinuity.

We now discuss the operator space version of the above embedding, which is already discussed in [4] . Note that in this case the embedding is positive, and becomes an isomorphism under the conditions weaker than that required in case of the Banach space projective tensor product. For operator spaces and, an operator from into is called completely nuclear if it lies in the image of the map [10] . The space of completely nuclear operators will be denoted by. This space has the natural operator

space structure determined by the identification.

For -algebras and, consider the map from into the dual of operator space injective tensor product given by

where is the natural completely isometric map, and [10] . Making use of the fact that the dual of the operator space projective tensor norm is the operator space injective ([10] , Proposition 8.1.2) and an application of Grothendieck’s theorem for jcb ([11] , Proposition 1) and the techniques of Lemma 2.1, we obtain the following:

Lemma 2.5 For -algebras and, the canonical map satisfies for all. In particular, is bi-continuous.

Proposition 2.6 For -algebras and, the natural map, defined by

, is bi-continuous satisfying for all.

Proof. By ([10] , Theorem 15.3.1) we have is locally reflexive operator space. Therefore, ([10] , Theorem

14.3.1) implies that can be identified with, where denotes the space of

completely integral operators from to. Now, the result follows by using the techniques of Proposition 2.2 and ([10] , Proposition 15.4.4).

By ([4] , Proposition 2.5), we have a continuous completely isometric map. Let

where is the natural embedding of into. Then clearly.

For a matrix ordered space and its dual space, we define -operation on by, and. Note that, for -algebras and, is a Banach -algebra ([12] , Proposition 3).

Theorem 2.7 For -algebras and, the natural embedding is -preserving positive bounded

map which satisfies for all.

Proof: Given, , , and,

On the other hand,. So in order to prove that is - preserving, we have to show that.

Note that, for and, ,

and hence the result follows from the separate -continuity of the bilinear forms corresponding to and.

Now given an algebraic element, where is defined as in [13] . For the positivity of

, we have to show that for. By ([13] , Theorem 1.9), it suffices to show that if then

where for all, and for all,.

Since is -dense in, so given we obtain a net which is -convergent to. Now note that. Hence the result follows.

The bi-continuity of the map follows as in Theorem 2.3.

Remark 2.8 By ([14] , Theorem 2.2), the natural embedding is completely isometric if one of the -algebras has the MAP.

We now discuss the isomorphism of this embedding. For, the map, for and, has a unique continuous extension to a map, with. The next proposition does not have counterpart in the Banach space context.

Proposition 2.9 For -algebras and, the family is total on.

Proof: Suppose that such that for all. Let with. Since, so for some, for all and, with. If is taken in the universal representation of then satisfies the

by ([10] , Theorem 15.1) and ([5] , 1.4.10). So there exists a net of finite rank -continuous mapping from to such that, and for all. Thus for and

, there exists such that for all. Since, we have such that. Since is a finite rank operator so, as in Lemma 2.1, for and. Thus, for

where, , , and, a norm convergent representation

in [10] ,. Given for all. Therefore, for any. Thus, giving that for all, and hence.

In particular, the map defined above is 1-1. Thus.

Now, as in Remark 2.4(iii), we have the following:

Corollary 2.10 Let and be -algebras such that every completely bounded operator from to is completely nuclear and the map defined in the Proposition 2.6 is onto. Then the natural embedding is an isomorphism map.

Remark 2.11 The embedding in the case of the Haagerup tensor product turns out to be completely isometric, which can be seen as below. For operator spaces, , using the fact that and ([5] , 1.6.7), the

map is completely isometric. Set

where. Then, clearly. By the self-duality of the Haagerup norm, the map is completely isometric. As in Theorem 2.3,

,

where is the completely isometric map from to, which further gives for any. Thus is completely isometric.

3. Closed Ideals in

It was shown in ([4] , Theorem 3.8) that if or is a simple -algebra then every closed ideal of is the product ideal, i.e. of the form or for closed ideal of and of. In the following, we generalize this result to the -algebra which has only a finite number of closed ideals. More precisely, it is shown that if one of the -algebras and has only finitely many closed ideals, then

every closed ideal in is precisely of the form, for some and closed ideals in

, in,. Thus obtaining the complete lattice of closed ideals of, , , where is an infinite dimensional separable Hilbert space, is a locally compact Hausdorff space, is any -algebra and is the multiplier algebra of, being a nonunital, non-elementary, separable, simple AF -algebra ([15] , Theorem 2). We would like to remark that in [4] the lattice of closed ideals of has already been explored.

Proposition 3.1 Let and be -algebras and a closed ideal in. If, the closure of in, then, where is the natural map from into.

Proof: Since so there exists a sequence such that as tends to infinity. Consider the identity map and. Of course, on, and hence by continuity. Thus and so by ([12] , Theorem 6).

The following lemma can be proved as a routine modification to the arguments of ([16] , Lemma 1.1).

Lemma 3.2 For closed ideals of and of,.

In order to prove our main result. We first investigate the inverse image of product ideals of for -algebras and, which is largely based on the ideas of ([10] , Proposition 7.1.7)

Proposition 3.3 For -algebras, and and the complete quotient maps,. Let and be closed ideals in and, respectively. Then

Proof: By ([4] , Proposition 3.2) and the Bipolar theorem, it suffices to show that

Let then and . Since, so for some, for all and. Define a bilinear map as

where and. Clearly, is well defined. Note that, for, and

, we have. For any, there are and with, such that . We can find such that,. By defini- tion, we may write

and

where, both have norm 1. Thus , and so. This shows that is jcb bilinear form. Thus it will determine a. We have for all and. This implies that on, and so by continuity. Now let . We may assume that. Then and. So with, and, [10] . Since and are complete quotient maps and , so it follows that. Hence

Since the annihilator is reverse ordering, so converse is trivial.

Now we are ready to prove the main result.

Theorem 3.4 If and are -algebras such that number of closed ideals in is finite. Then every closed ideal in is a finite sum of product ideals.

Proof. Proof is by induction on, the number of closed ideals in counting both and. If then the result follows directly by ([4] , Theorem 3.8). Suppose that the result is true for all - algebras with. Let be a -algebra with.

Since there are only finitely many closed ideals in so there exists a minimal non-zero closed ideal, say, which is simple by definition. Let be a closed ideal in then is a closed ideal in.

So it is equal to for some closed ideal in by ([4] , Theorem 3.8). Consider the closed ideal,

the closure of in, where is an injective map ([11] , Theorem 1). Then for some closed ideal in by ([17] , Proposition 5.2). We first show that. Since the map is injective so. Thus,

which by using ([18] , Corollary 4.6), ([19] , Proposition 4), and Lemma 3.2, gives that and so. To see the equality, let. Take any then so it belongs to by Proposi- tion 3.1. Thus. Hence.

As in ([17] , Theorem 5.3), for. Thus by Lemma 3.2. Since cannot contain, so. Thus, which is a closed

ideal in, is a finite sum of product ideals by induction hypothesis. Let then clearly

contains. Corresponding to the complete quotient map, we have a quotient map with kernel and is a closed ideal of ([19] , Lemma 2).

Also and so by the induction hypothesis

where and are closed ideals in and, for, respectively. Thus, by ([19] , Lemma 2)

and Theorem 3.3,. So is a finite sum of product ideal and hence closed by ([4] , Proposition 3.2).

We now claim that.

Let. Since the closed ideal has a bounded approximate identity

so there exist such that and belongs to the least closed ideal of

containing ([20] , 11, Corollary 11). This implies that so. Hence. Therefore is a finite sum of product ideals.

4. Inner Automorphisms of

For unital -algebras and, isometric automorphism of is either of the form or, where, , and are isometric isomorphisms ([11] , Theorem 4). In the following, we characterize the isometric inner -automorphisms of completely.

Proposition 4.1 For unital -algebras and, the map is inner automorphism of (resp.) if and only if is inner automorphism of and is inner automorphism of.

Proof: Suppose that is implemented by. We will show that is implemented by, where is -homomorphism from into [11] . It is easy to see that.

So, for,. As is -

dense in, so is implemented by. Hence the result follows from ([21] , Theorem 1). Converse is trivial.

We now characterize the isometric inner automorphism of for -algebras and other than.

Theorem 4.2 For unital -algebras and other than for some, the isometric inner - automorphism of is of the form, where and are inner -automorphisms of and, respectively.

Proof: Suppose that is the isometric inner -automorphism of. So

where and are -automorphisms of and, respectively or

where and are -isomorphisms, is a flip map [11] . In view of Proposition 4.1, it suffices to show that the second case will never arise for -algebras and other than. Let be a proper closed ideal in and, which is a closed ideal in by ([12] , Theorem 5). Since is inner so it preserves. Thus, for any,. Therefore [19] , which further gives that. Hence and so is simple. Similarly, one can show that is simple. By hypothesis there exists which implements so

that for all and. Choose such that, , and. Thus, for and, we have , hence .

Now choose such that. Therefore, for all. Take any, being an isomorphism, there exists a unique such that. Thus for any. Now define a finite dimensional subspace of by

The above inequality implies that, where is the closed ball center at and radius. If is proper then Riesz Lemma implies that for there exists such that and. Since for any, so we can choose such that, and, because, a contradiction arises. Therefore,. Thus, by the classical Wedderburn-Artin

Theorem, for some. Similarly, for some.

However, by ([11] , Theorem 5), for unital -algebras and with at least one being non-commutative, isometric inner automorphism of is of the form, where and are inner automorphisms of and of, respec- tively.

Corollary 4.3 For an infinite dimensional separable Hilbert space, every inner automorphism of is of the form, where and are inner automorphisms of.

We now give an equivalent form of Proposition 4.1 in case of operator algebras. For operator algebras and, we do not know if (or) is inner then and are inner or not. However, if one of the automorphism is an identity map then we have an affirmative answer for the Haagerup tensor product. In order to prove this, we need the following results.

Proposition 4.4 For operator spaces and, the family is total on.

Proof: For, assume that for all. We can assume that. Therefore,

for a norm convergent representation in, where and are strongly independent with and. Then we have for all. From the

strongly independence of, choose linear functionals such that

where are the standard basis for by the equivalent form of ([17] , Lemma 2.2). Thus and so. Because was arbitrary, we conclude that for each, hence

.

Corollary 4.5 For operator algebras and, if and are completely contractive automorphisms of and, respectively. Then is a completely contractive automorphism of.

Proof: By the functoriality of the Haagerup tensor product, the map is comple-

tely contractive. One can see that is an algebra homomorphism. Let be a norm con-

vergent representation in. Since and are bijective maps, so there exist unique and

, for each, such that. By [22] , there is a new norm on and with respect

to that and become a new operator algebras, say and, and the natural maps from to, from to and their inverses are completely bounded, and the maps and are completely isometric. Therefore, is completely isometric, so for all positive integers

This shows that the partial sums of form a Cauchy sequence in, and so we may define an element. Then, clearly. Thus the map is onto. To prove the injectivity of the map, let for. Then, for a norm con- vergent representation in, we have. Thus, for any,. But is one-to-one, so. Now Proposition 4.4 yields that. Again by applying the same technique we obtain.

By the above corollary, for operator algebras and and automorphisms of and of, it is clear that if and are inner then is.

In the following, by a -reduced operator algebra we mean an operator algebra having isometric involution with respect to which it is -reduced, and for any -reduced operator algebra having approximate identity, we denote by the set of all pure states of.

Corollary 4.6 For -reduced operator algebra having approximate identity and any operator algebra, the family is total on.

Proof: Using ([23] , Proposition 2.5.5), we have, where is the set of continuous positive forms on of norm less than equal to 1. Therefore, if for all then

for all. Thus for any and. Since the algebra is -reduced, so

it admits a faithful -representation, say, on some Hilbert space, say. For a fix in the closed unit ball of, define as for. One can easily verify that. As is

faithful so is one-to-one. Therefore, for any and hence the result follows from Proposition 4.4.

Corollary 4.7 For any operator algebra and -reduced operator algebra having approximate identity, the family is total on.

The following can be proved on the similar lines as those in ([21] , Lemma 2) by using ([23] , Proposition 2.5.4), so we skip the proof.

Lemma 4.8 For unital Banach -algebra and any Banach algebra and a pure state of, we have for and (Similarly, for any Banach algebra and unital Banach -algebra, for and,).

Theorem 4.9 Let and be unital operator algebras. Suppose that is -reduced and has a completely contractive outer automorphism. Then has a completely contractive outer automorphism.

Proof: Let be a completely contractive outer automorphism. Define a map from into

as. By Corollary 4.5, is a completely contractive automorphism of

. Assume that is a inner automorphism implemented by. Then. As so we can find the pure state on such that by Corollary 4.7. Let. Note that for any we have. This implies that, the relative commutant of in, which is by ([18] , Corollary 4.7). For,

by the module property of the slice map. Since

is invertible, so is invertible by Lemma 4.8. Therefore, and hence is inner, a contradiction. Thus is an outer automorphism.

References

NOTES

^*2010 Mathematics Subject Classification. Primary 46L06, Secondary 46L07, 47L25.