ABSTRACT

In a Euclidean space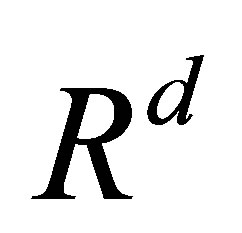, the Lebesgue-Stieltjes integral of set-valued stochastic processes with respect to real valued finite variation process is defined directly by employing all integrably bounded selections instead of taking the decomposable closure appearing in some existed references. We shall show that this kind of integral is measurable, continuous in under the Hausdorff metric and 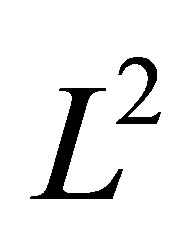-bounded.

1. Introduction

Recently, integrals for set-valued stochastic processes with respect to Brownian motion, martingales and the Lebesgue measure have received much attention.

In 1997, Kisielewicz ([1]) defined the integral of setvalued process as a subset of space, but he didn’t consider the measurability of the integral. In 1999, Kim and Kim [2] used the definition of stochastic integrals of set-valued stochastic process with respect to the Brownian motion. They called it Aumann ([3]) type It integrals. In [4], Jung and Kim modified the definition by taking the decomposable closure such that the integral is measurable. Li and Ren [5] modified Jung and Kim’s definition by considering the predictable set-valued stochastic process as a set-valued random variable in the product space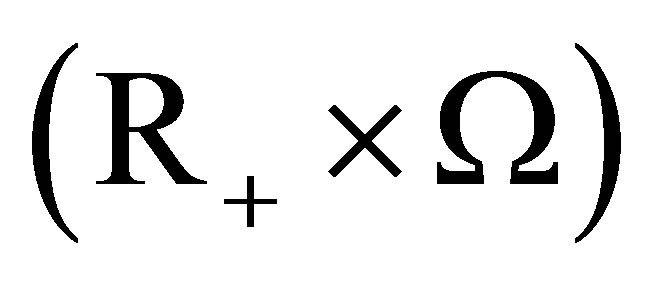, and the measurability and decomposability also were based on product -algebra. After that, Zhang et al. ([6,7]) studied the set-valued integrals with respect to the martingale and Brownian motion.

Stochastic differential inclusions and set-valued stochastic differential (or integral) equations are employed to model the problems with not only randomness but also impreciseness. Recently, there are some references related to set-valued differential equations such as [8-13] etc.

Concerning to the integral with respect to finite variation processes, Malinowski and Michta [12] give the notion of set-valued integral with respect to single valued finite variation but without considering the measurability. Z.Wang and R.Wang [14] defined the Lebesgue-Stieltjes stochastic integral of single valued stochastic processes with respect to set-valued finite variation processes (refer to [14] for the detail).

In this paper, different from the definition in [14], based on the Definition 3.1 in [12], we will study the Lebesgue-Stieltjes integral of set-valued stochastic processes with respect to single valued finite variation process. We shall prove the measurability of integral, namely, it is a set-valued random, which is similar to the classical stochastic integral.

This paper is organized as follows: in section 2, we present some notions and facts on set-valued random variables; in section 3, we shall give the definition of integral of set-valued stochastic processes with respect to finite variation process and then prove the measurability and -boundedness.

2. Preliminaries

We denote the set of all natural numbers, 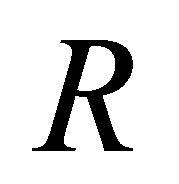the set of all real numbers, 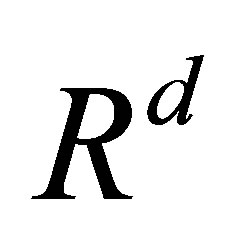the d-dimensional Euclidean space with the usual norm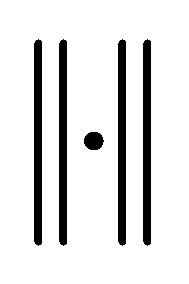, 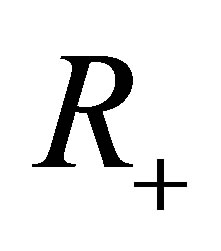the set of all nonnegative numbers. Let be a complete probability space, 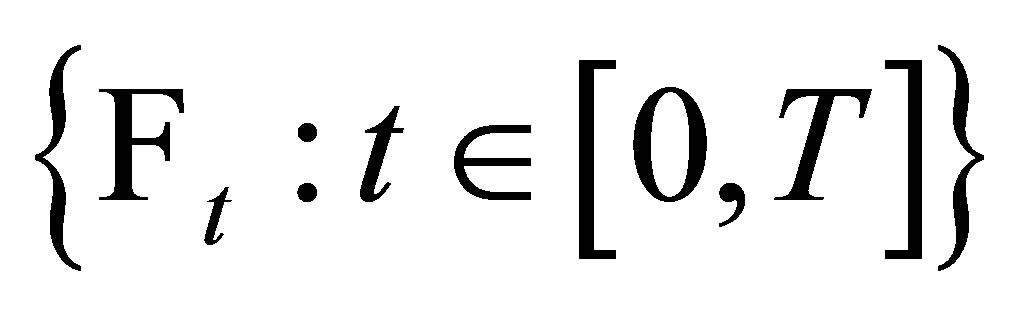a -field filtration satisfying the usual conditions. Let 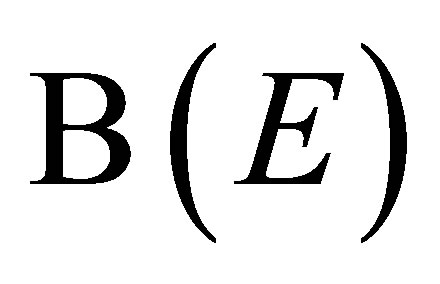be a Borel field of a topological space.

Let 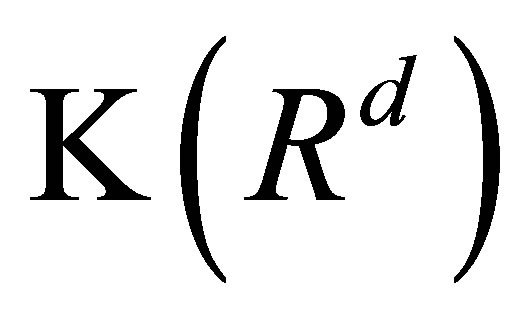(resp.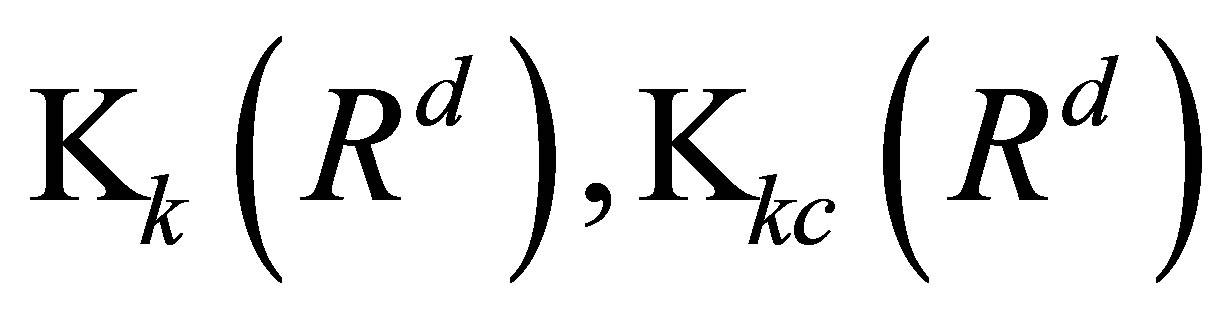) be the family of all nonempty, closed (resp. nonempty compact, nonempty compact convex) subsets of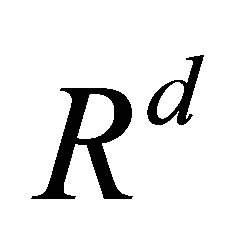. For any 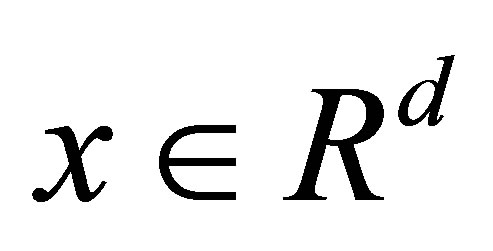and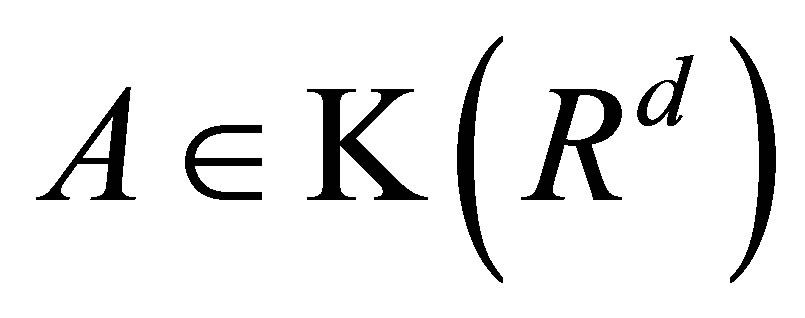, define the distance between and A by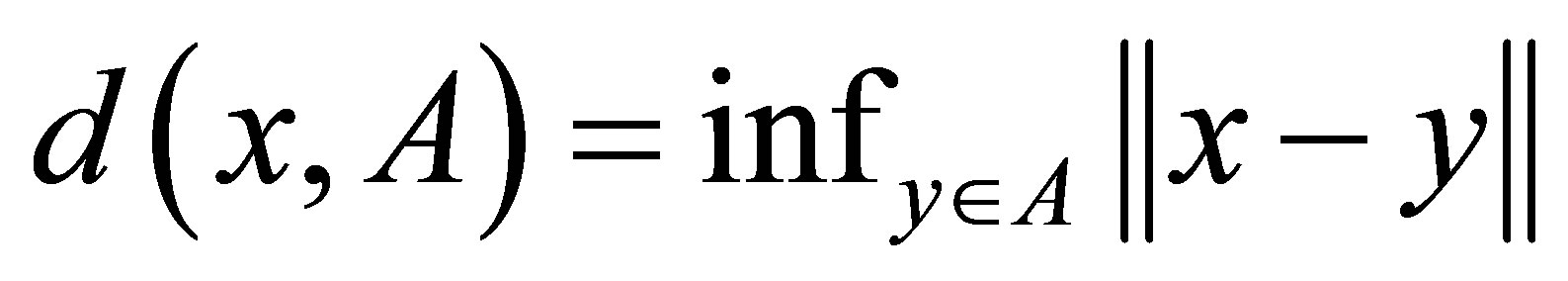. The Hausdorff metric 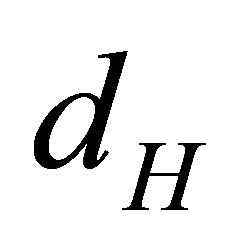on 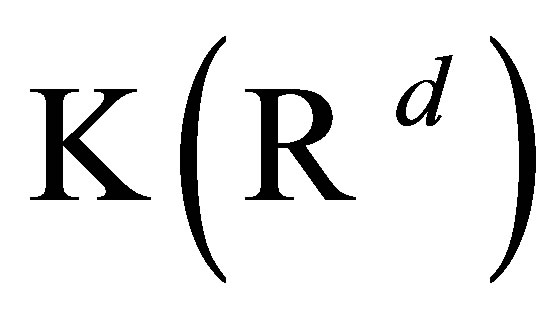(see e.g. [15]) is defined by

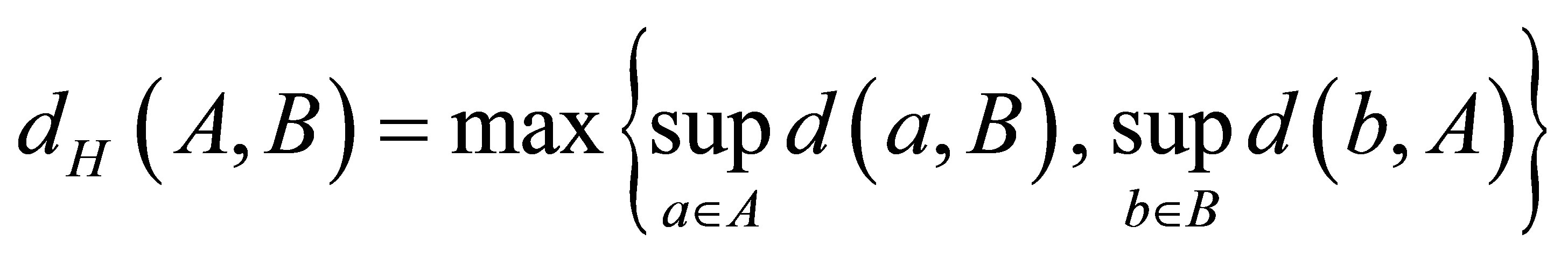(1)

.

Denote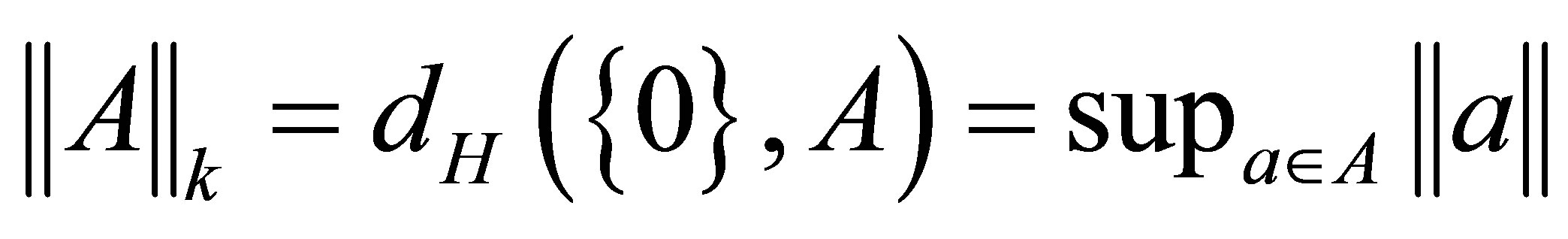. For , we have

For 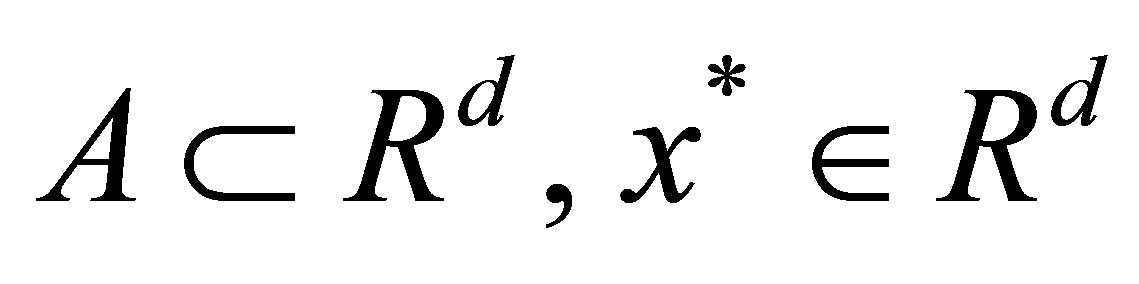the support function of 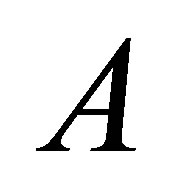is defined as follows:

: the set of all—valued Borel measurable functions 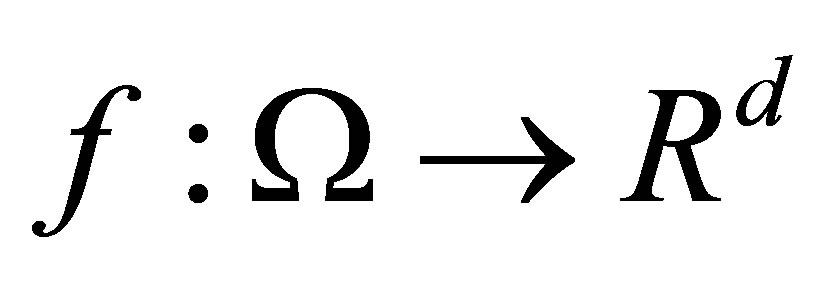such that the norm

is finite. 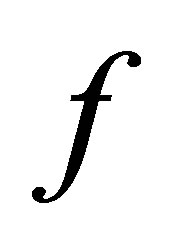is called -integrable if.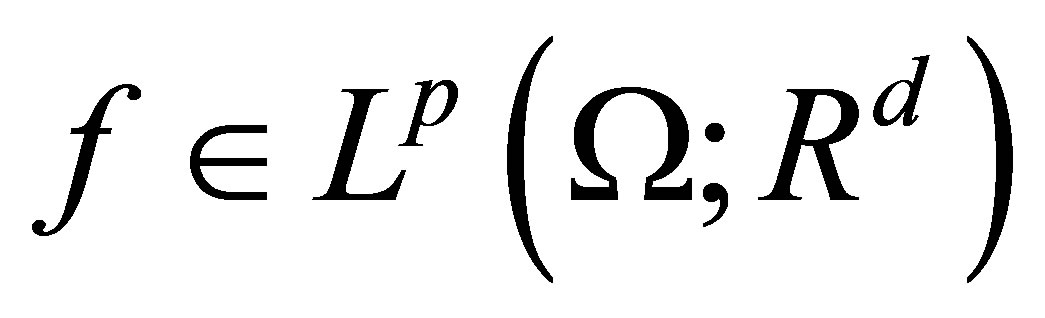

A set-valued function 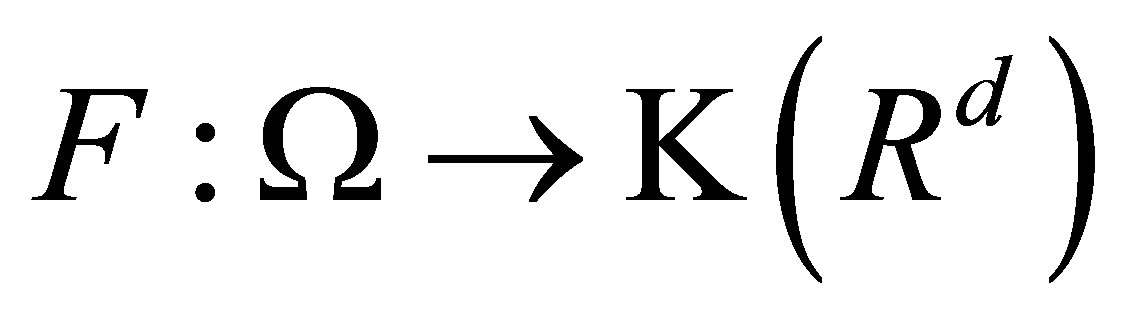is said to be measurable if for any open set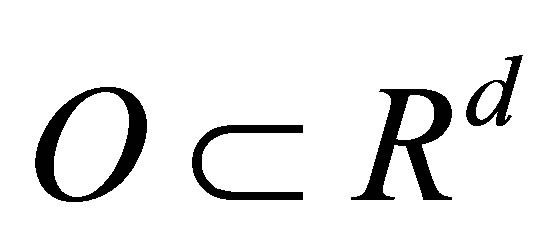, the inverse 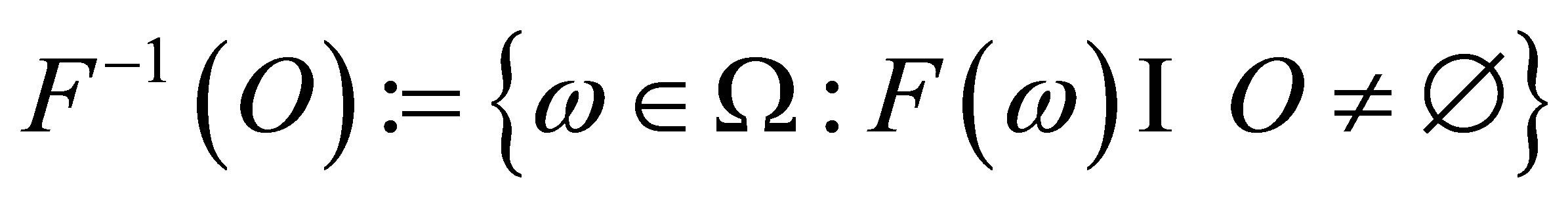belongs to. Such a function is called a set-valued random variable.

Let 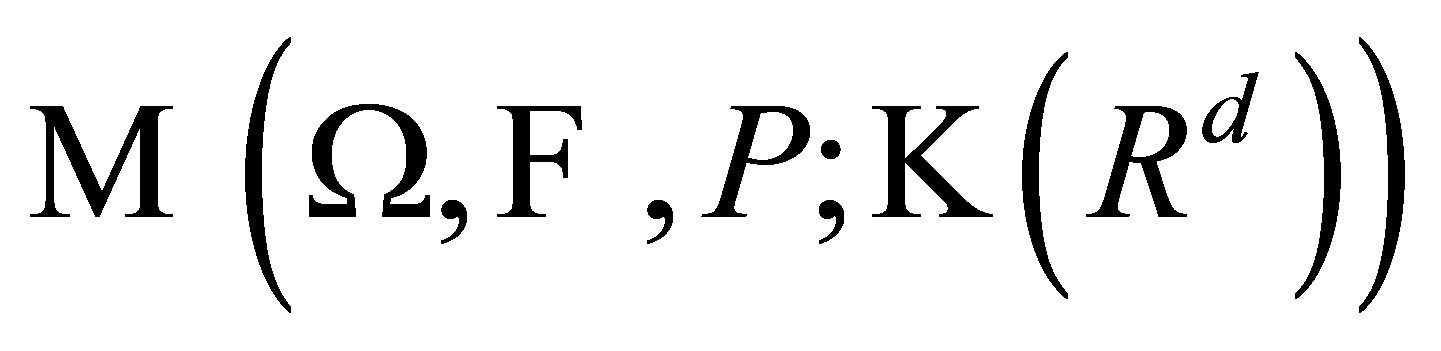(resp.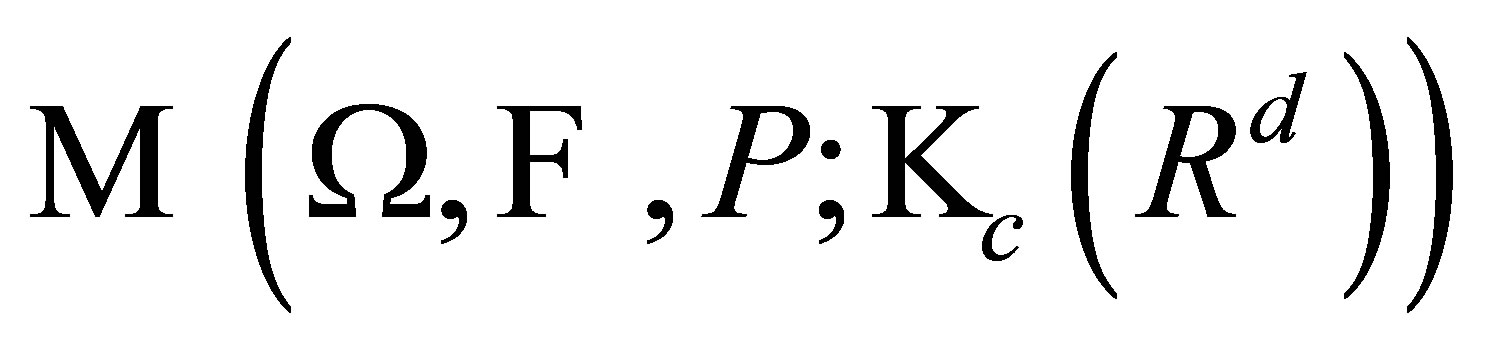,) be the family of all measurable -valued (resp. -valued) functions, briefly by 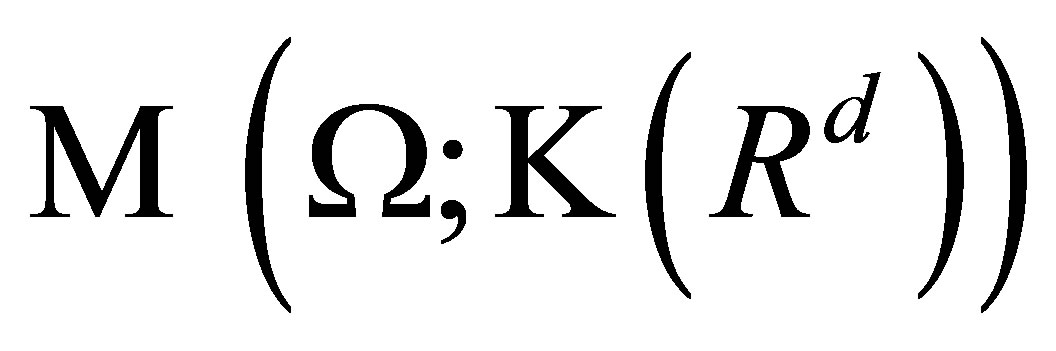(resp. 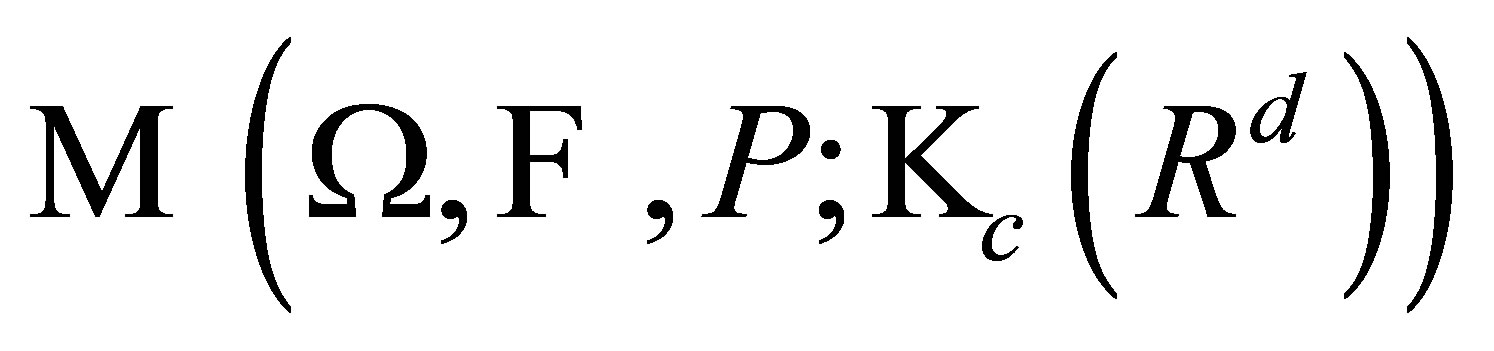,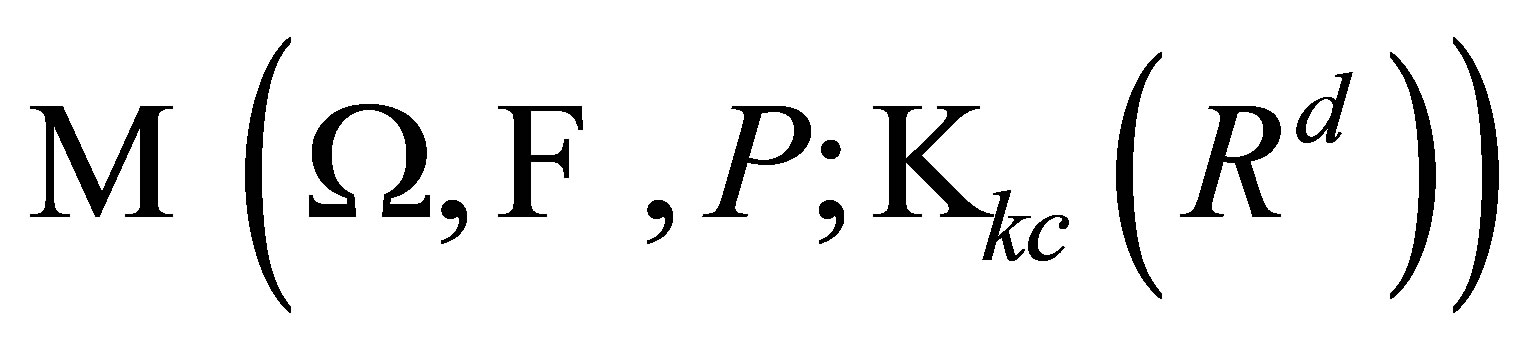. For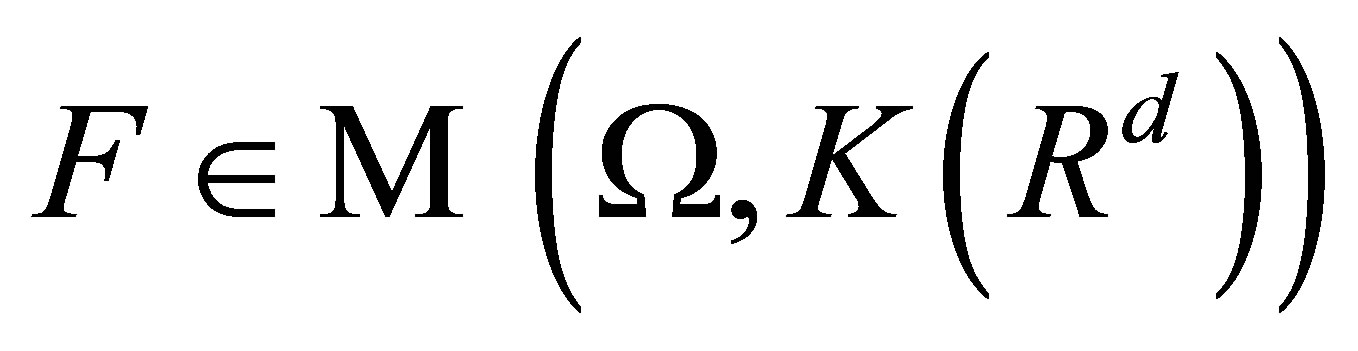, the family of all -integrable selections is defined by

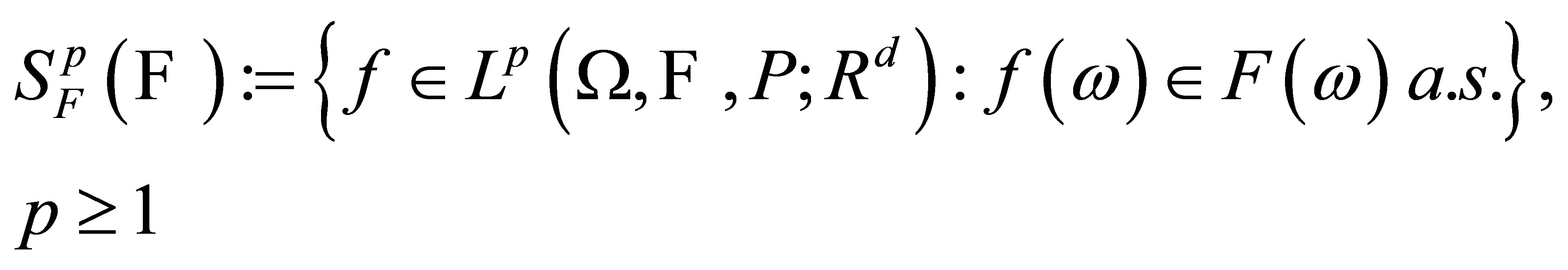(2)

In the following, is denoted briefly by.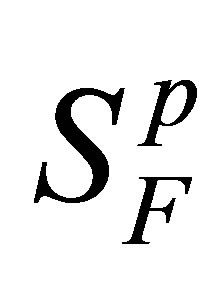

A set-valued random variable is said to be integrable if 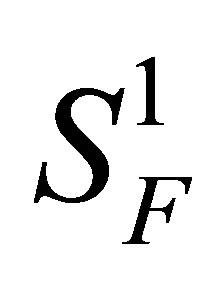is nonempty. is called -integrably bounded if there exits 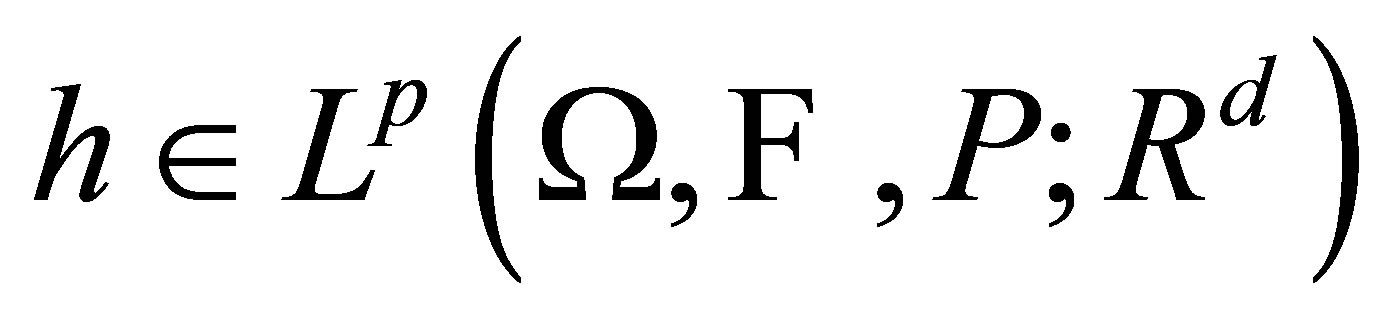s.t. for all, almost surely.

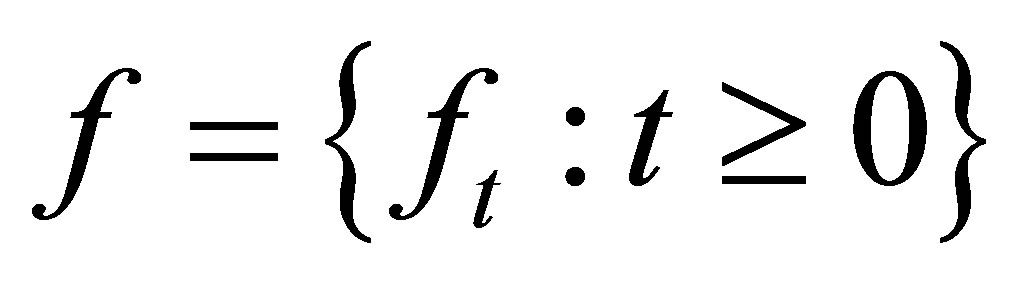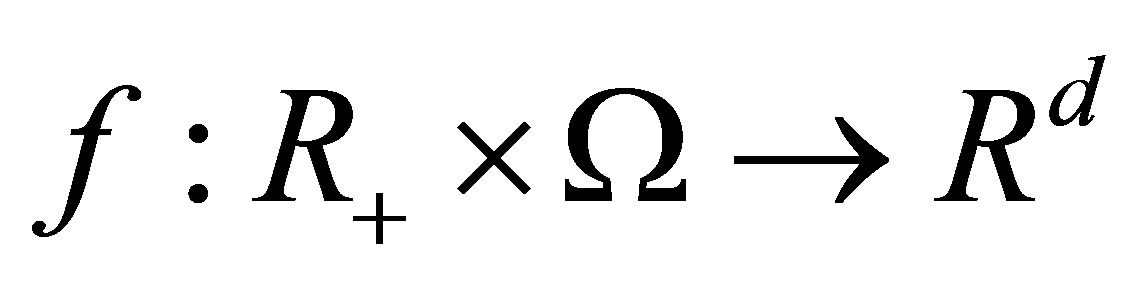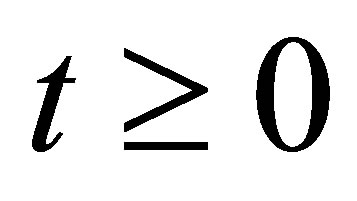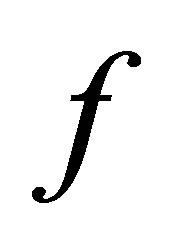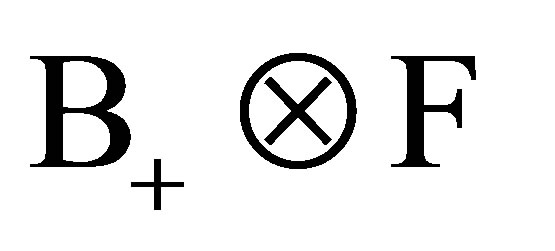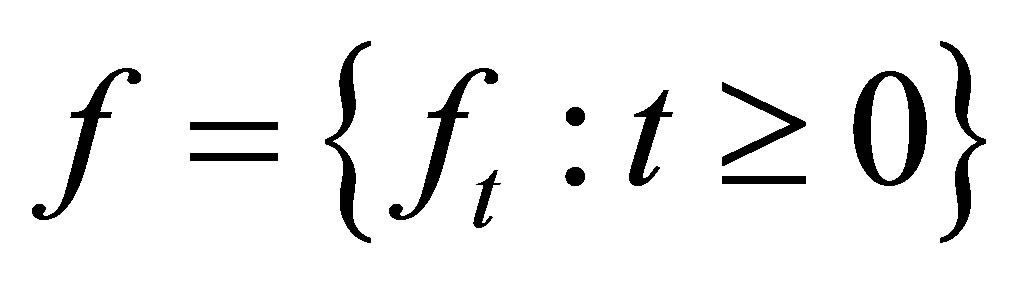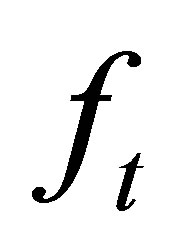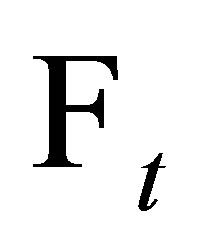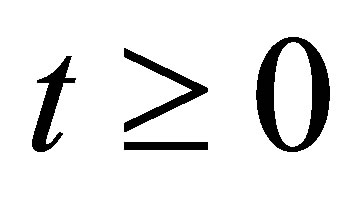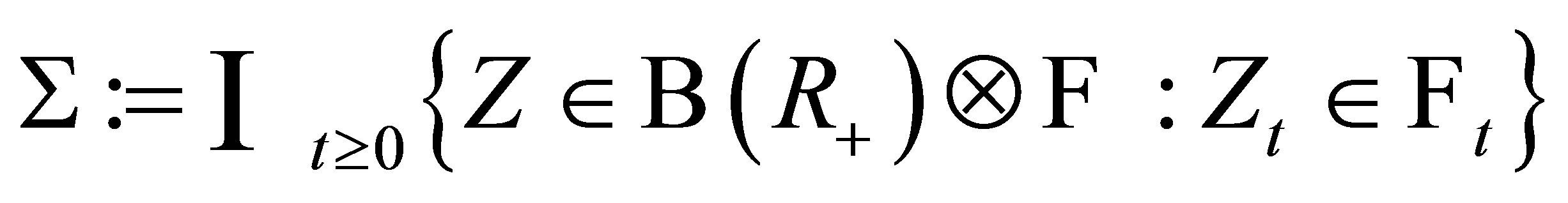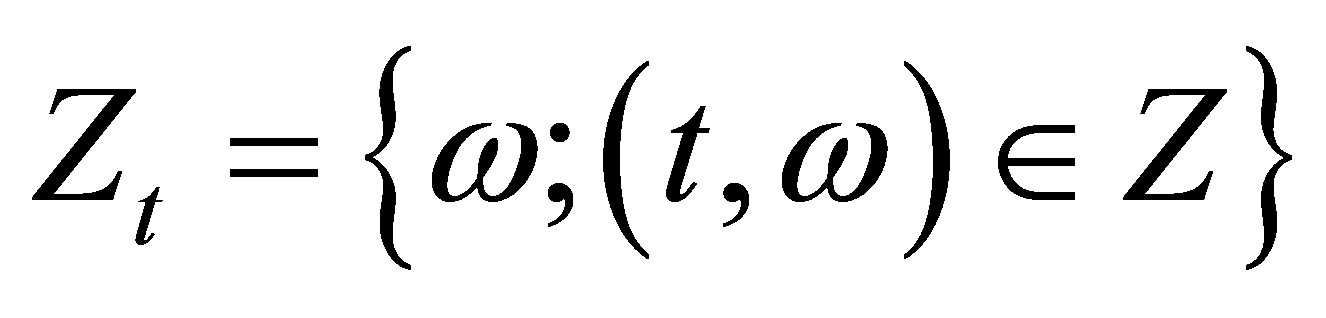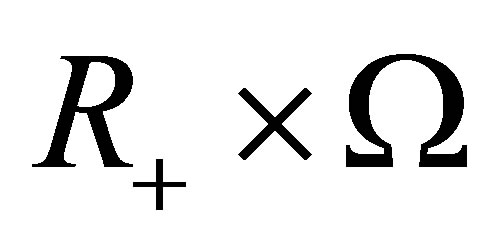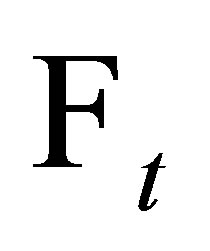An -valued stochastic process (or denoted by) is defined as a function with the -measurable section, for. We say is measurable if is - measurable. The process is called -adapted if is -measurable for every. Let, where . We know that is a -algebra on. A function is measurable and -adapted if and only if it is -measurable ([8]).

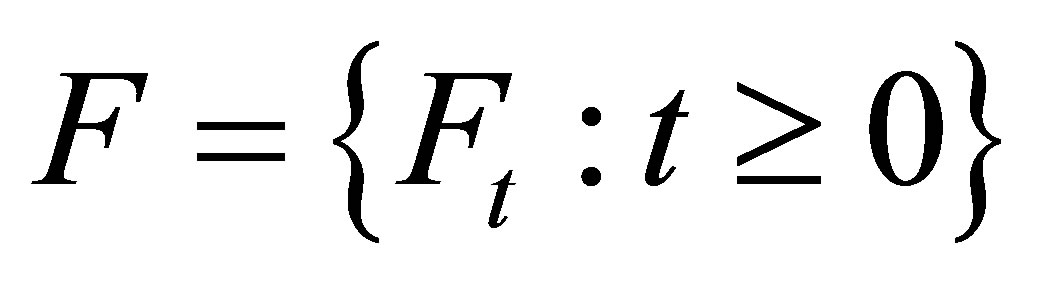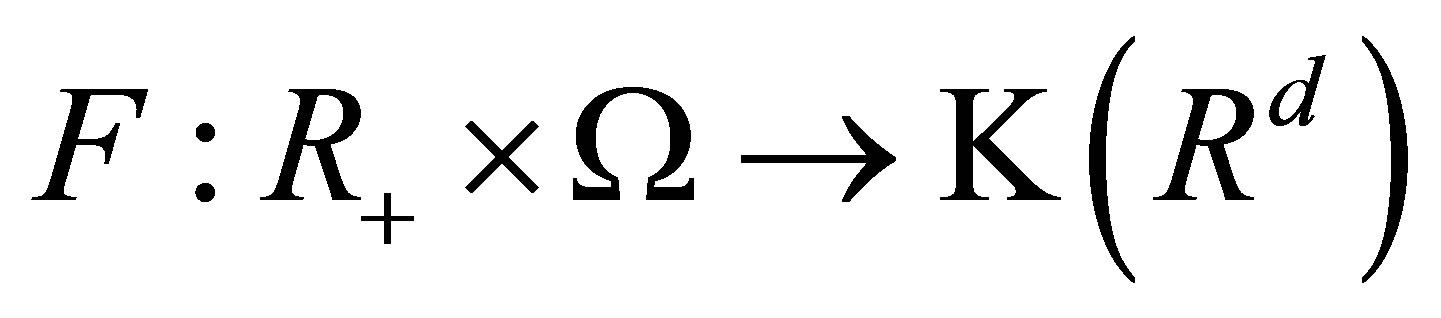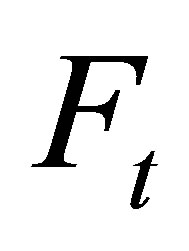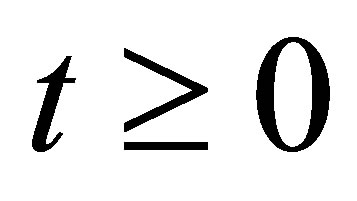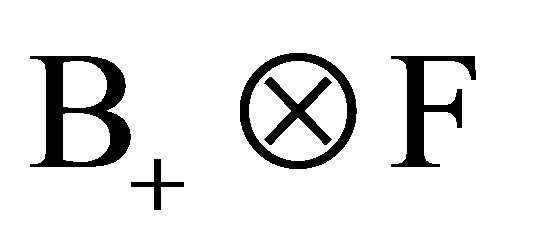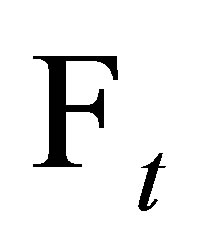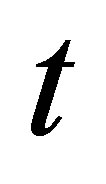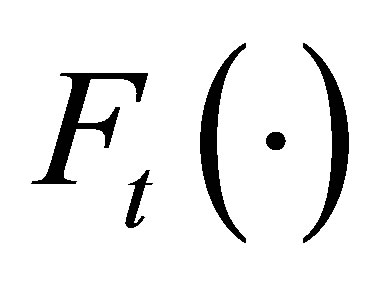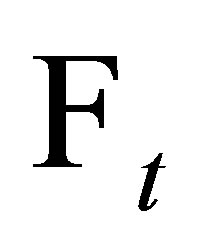In a fashion similar to the -valued stochastic processes, a set-valued stochastic process is defined as a set-valued function with -measurable section for. It is called measurable if it is -measurable, and - adapted if for any fixed, is -measurable. 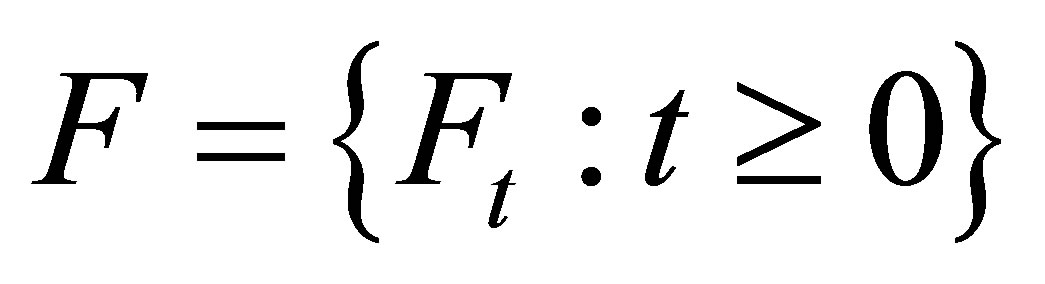is measurable and -adapted if and only if it is -measurable. 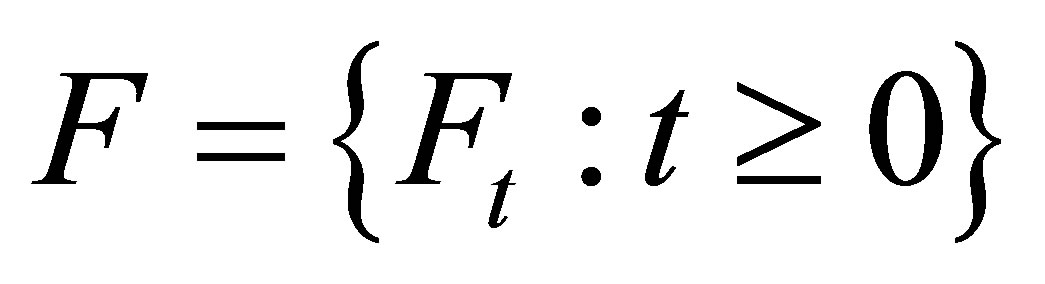is called  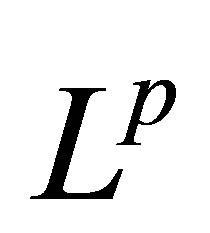-integrable if every 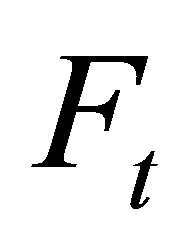is 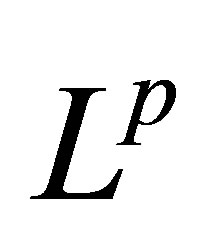-integrable.

3. Set-Valued Stochastic Integral w.r.t Finite Variation Processes

Let 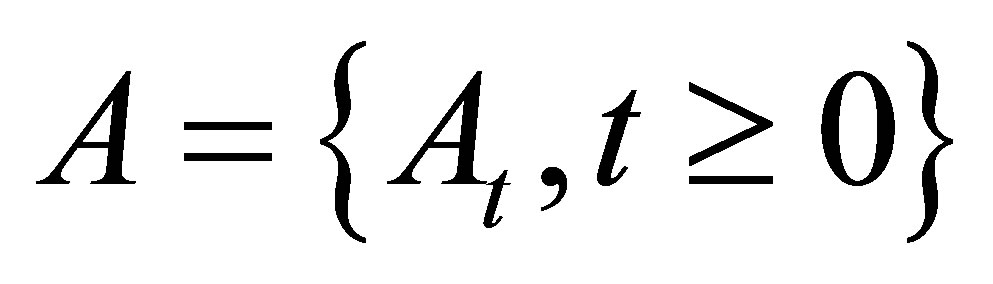be a real valued 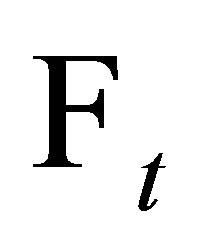-adapted measurable process with finite variation and continuous sample trajectories a.s. from the origin. That is to say, for each compact interval 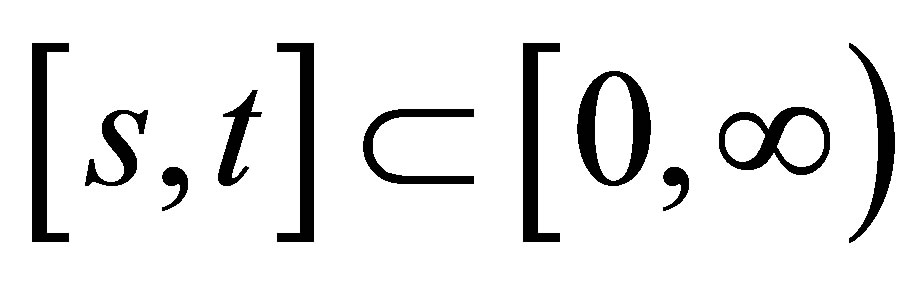and any partition 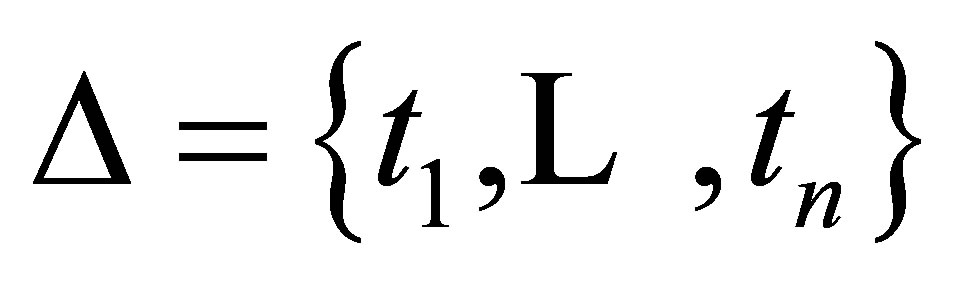of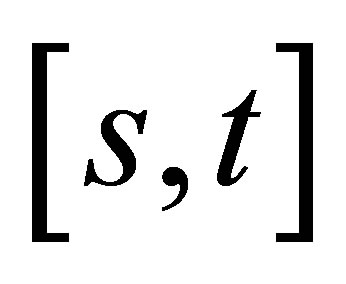, the total variation

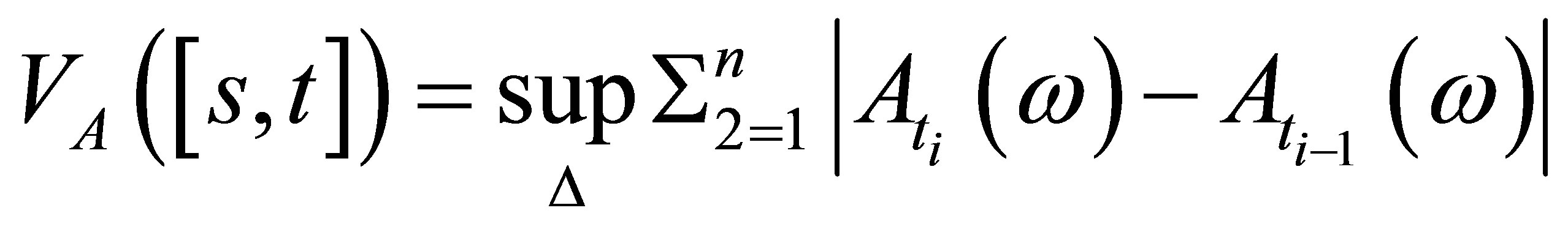
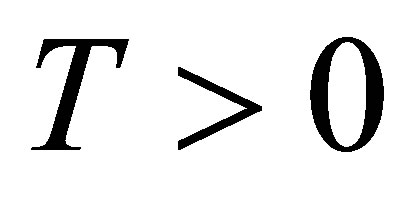is finite and a.s. Then for any, the process 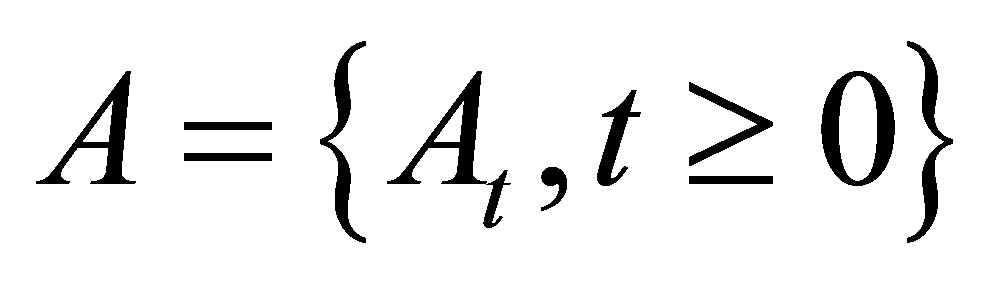can generate a random measure denoted by 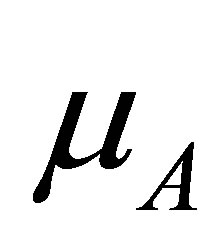in the space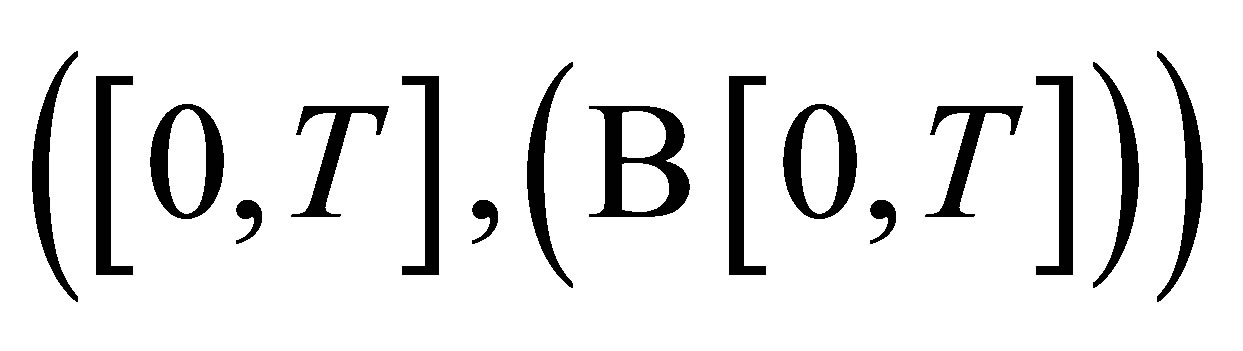. For any, let

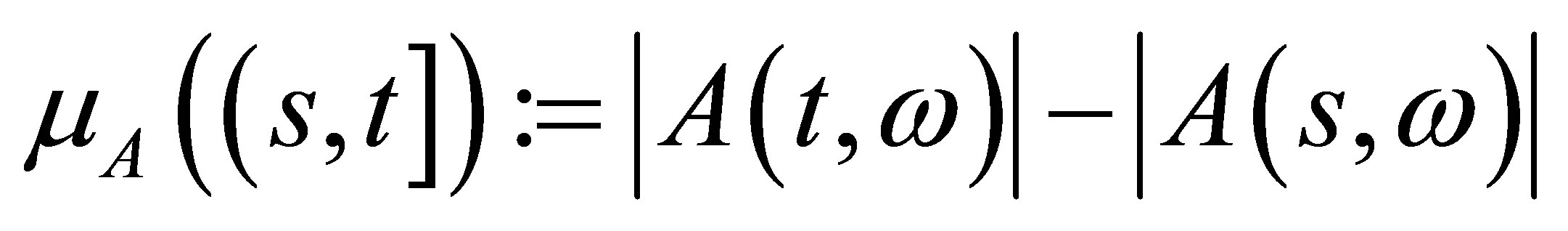
where 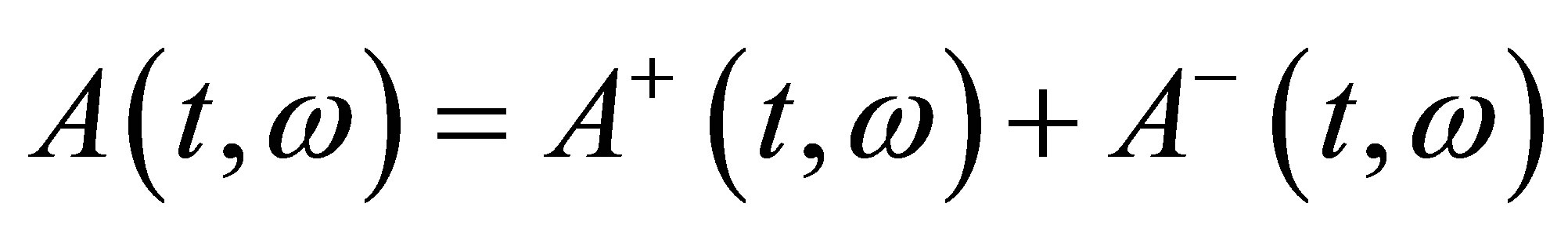is the decomposition of, 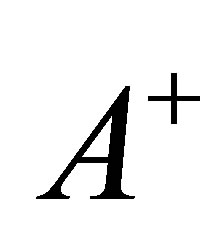and 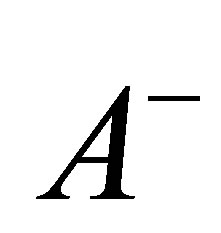are non-negative and nondecreasing processes,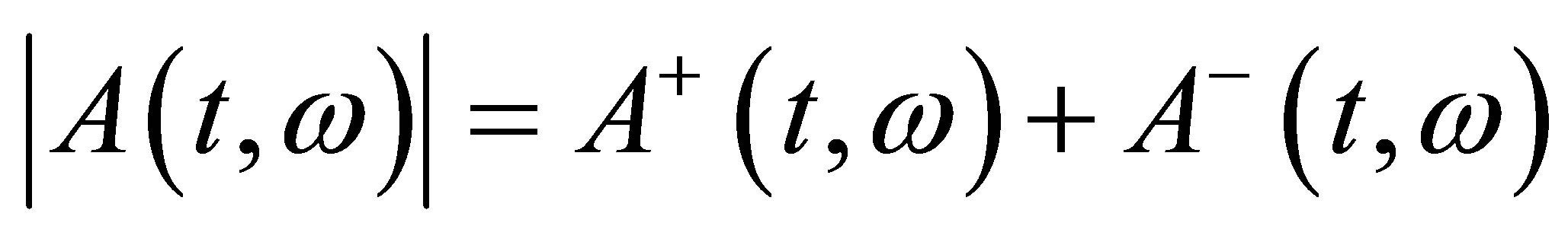. In the product space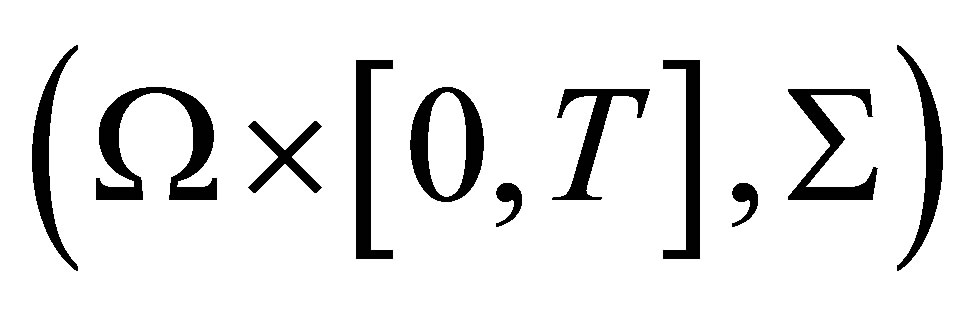, set

(3)

for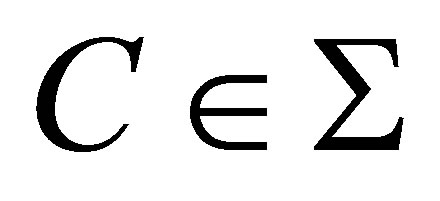, where 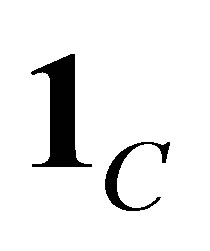is the index function. Then the set function is a finite measure in the measurable space 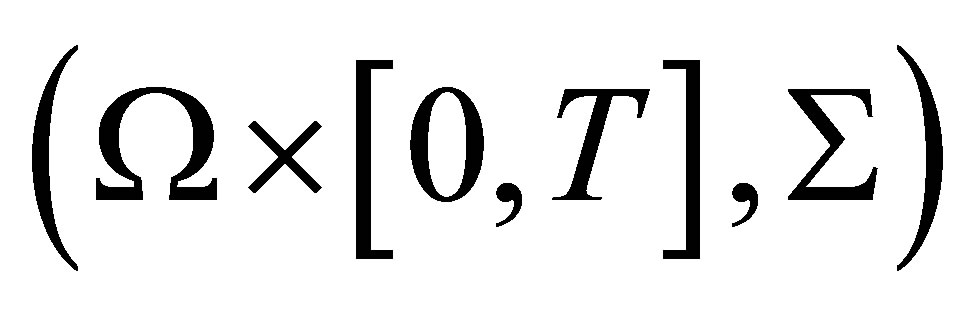if and only if . In the following we always assume.

Let 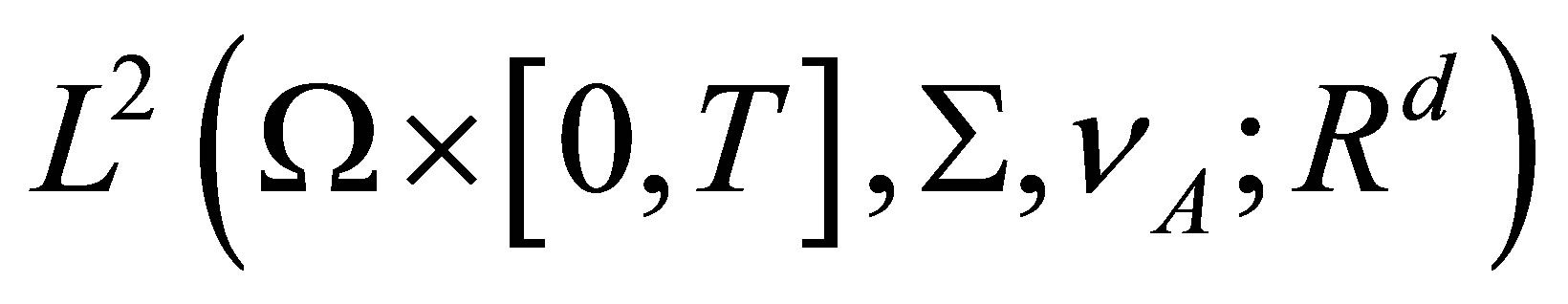be the family of all -measurable 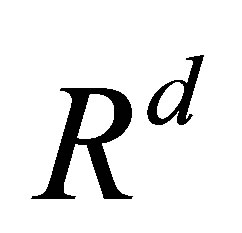-valued stochastic processes 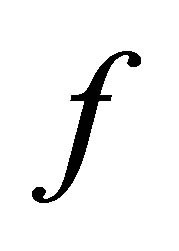such that

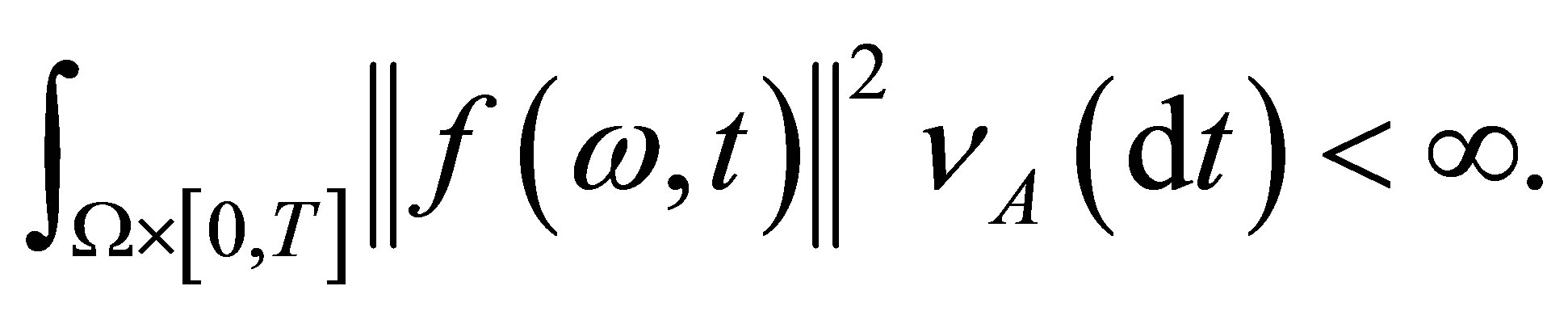
For any 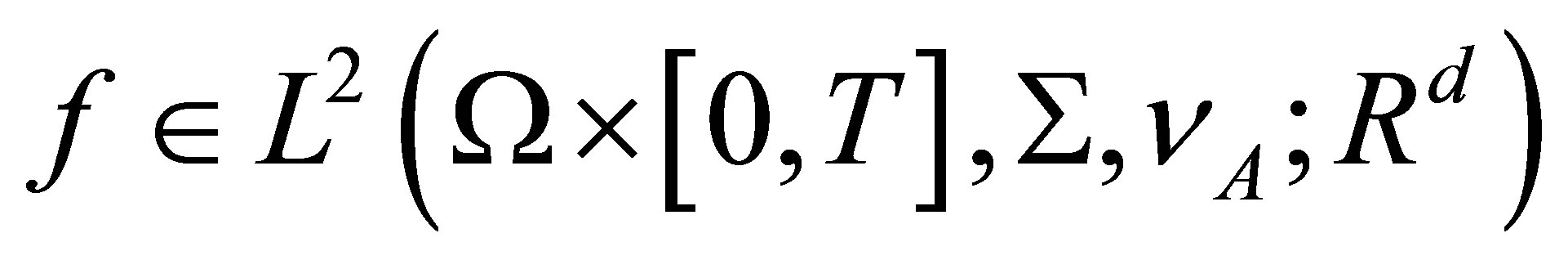and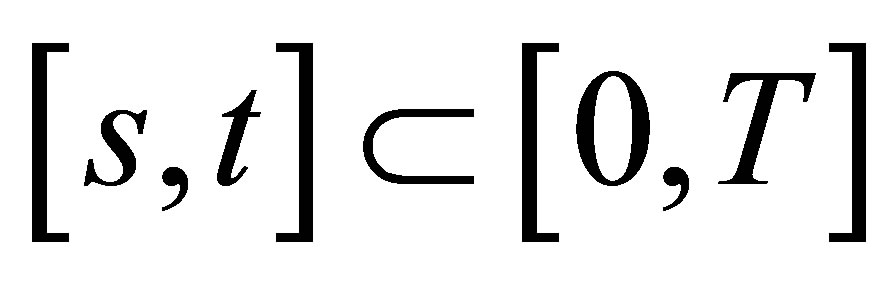, the stochastic Lebesgue-Stieltjes integral 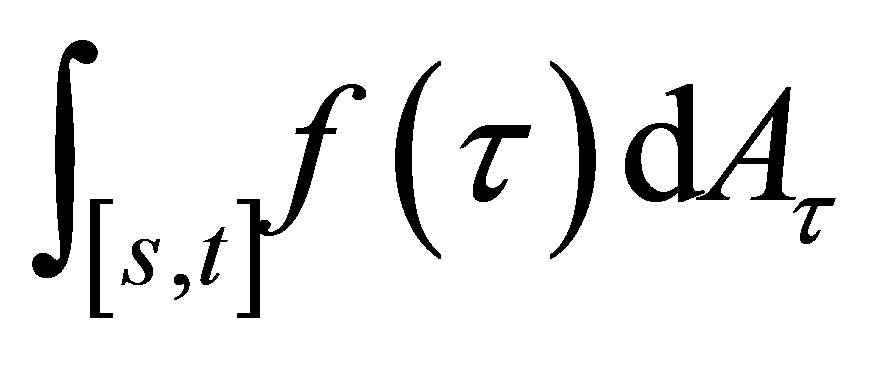is defined by the Bochner integral 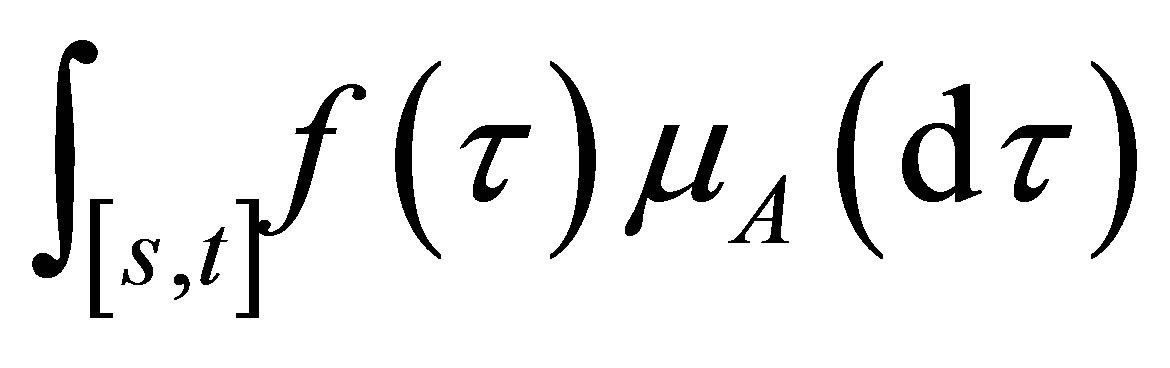pathby-path. One can show that the integral process

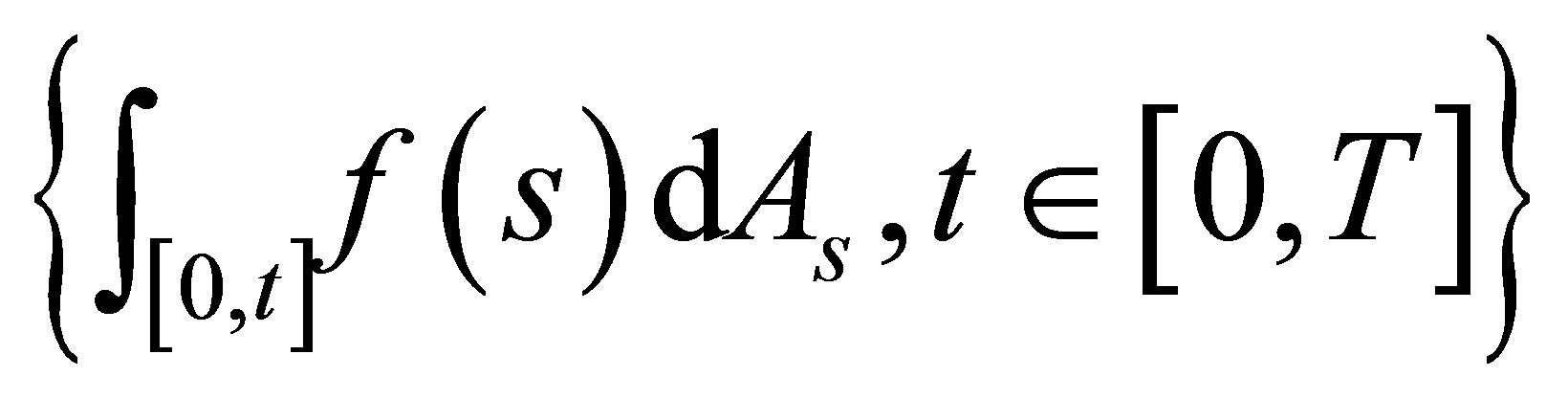is -measurable.

Note: in [12], the integrand is assumed being predictable, in fact the integrand can be relaxed to the - measurable class since the integrator 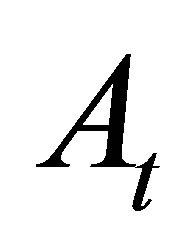is continuous.

Let 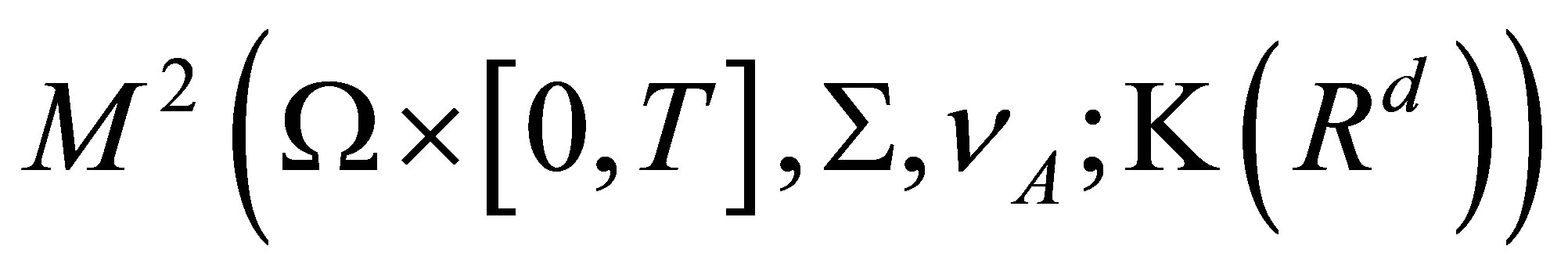be the family of all -measurable -valued stochastic processes such that

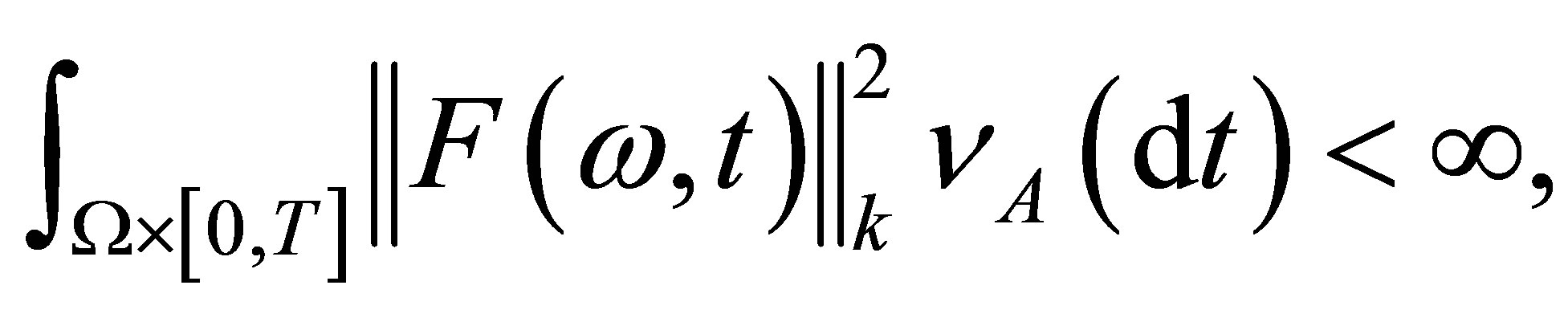
where. For any 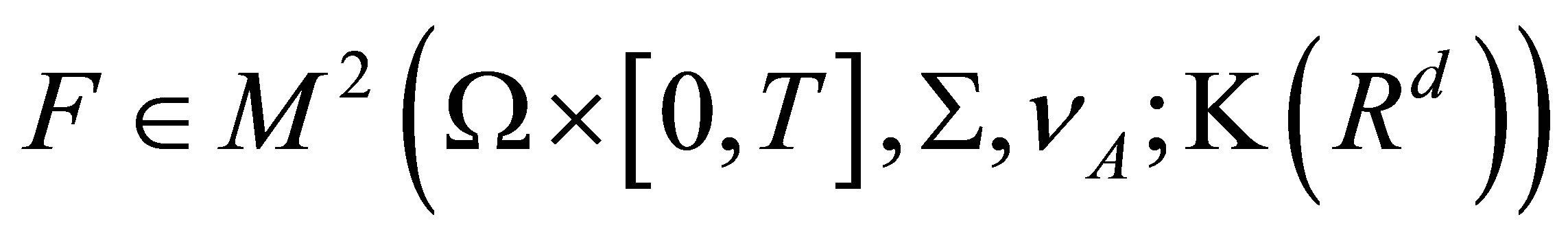, set

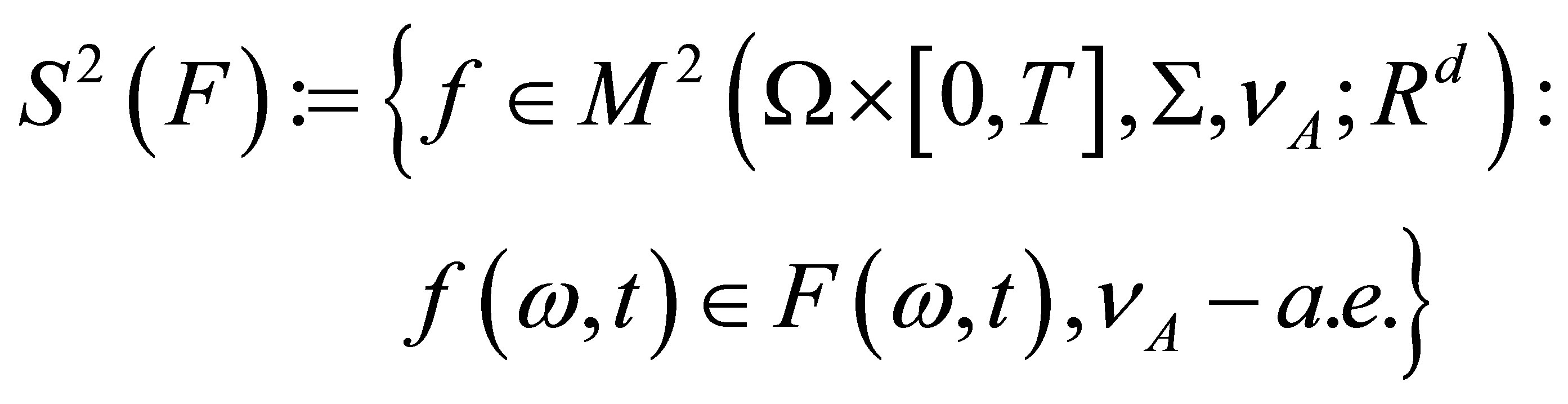(4)

Definition 1. (see [12]) For a set-valued stochastic process the set-valued stochastic Lebesgue-Stieltjes integral (over interval) of with respect to the finite variation continuous process is the set

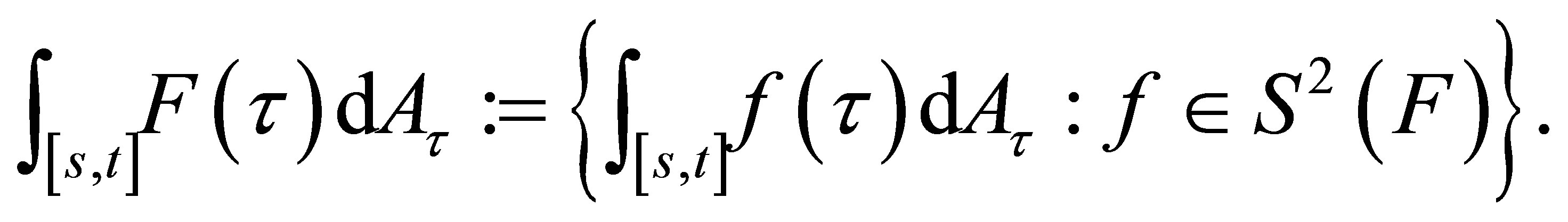
In [12], the authors call this kind of integral as trajectory integral since they consider it as a

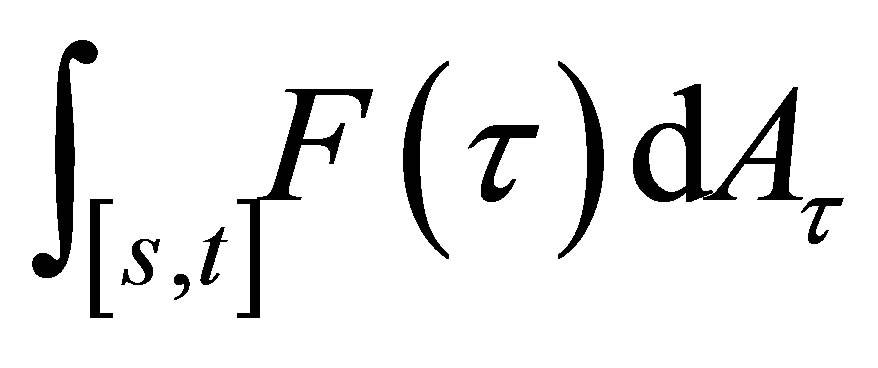-valued random variable. Here, we shall consider it as a subset of and show the measurability with respect to, which is very different from the way in [12], also different from other references such as [10,16,17] etc. In fact, for almost every, the above integral is a subset of. In the following, we shall assume the - algebra 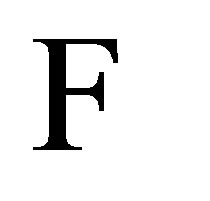is separable w.r.t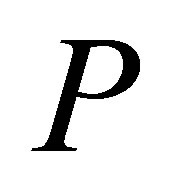. In addition, 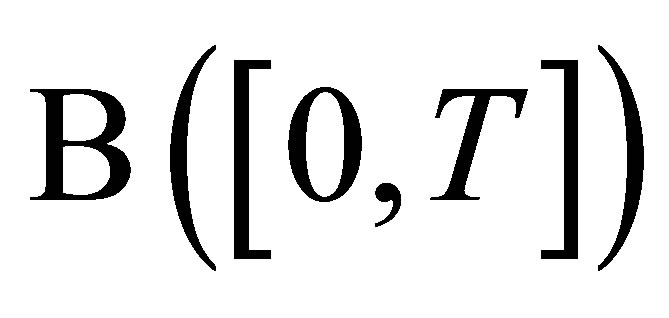is separable and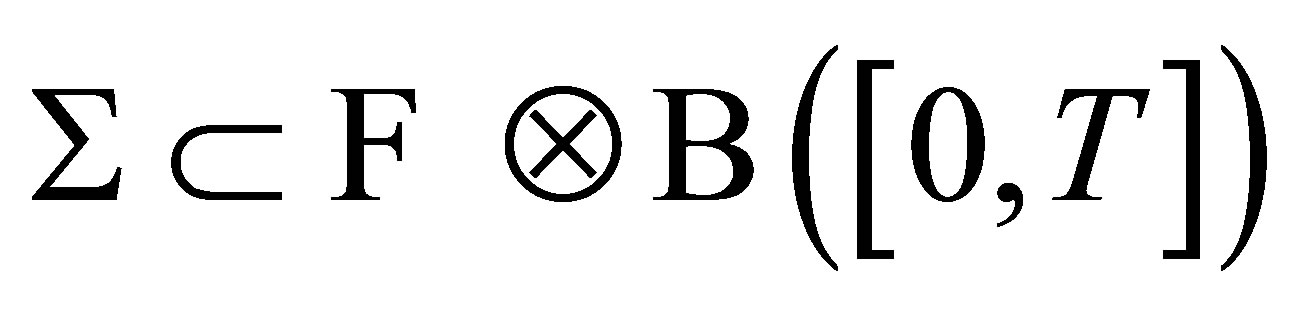, then one can get is separable. 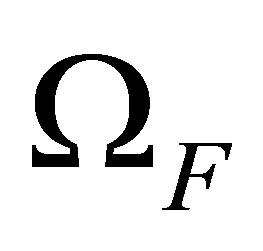Therefore we can find an - measurable set, such that 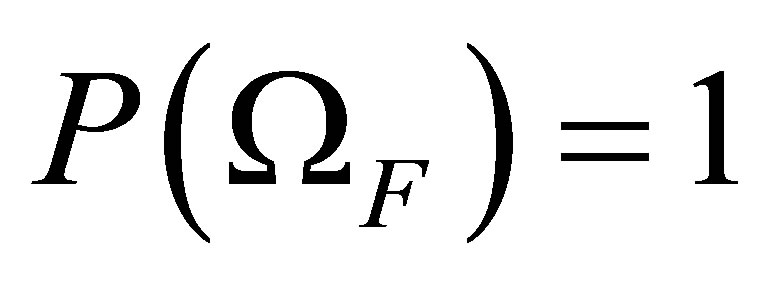and for every

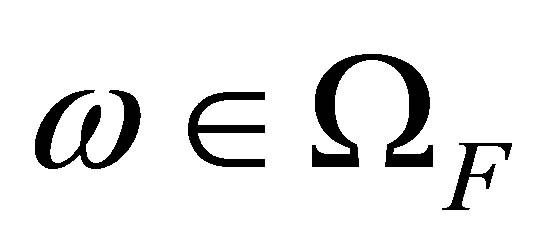, the integral is defined path-bypath. For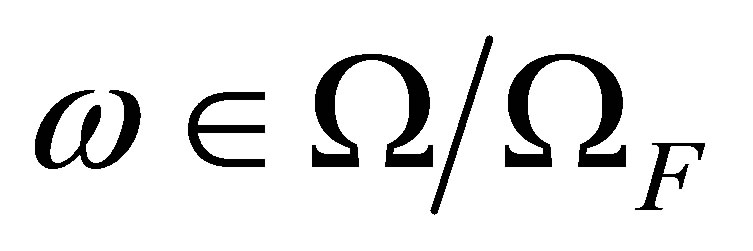, set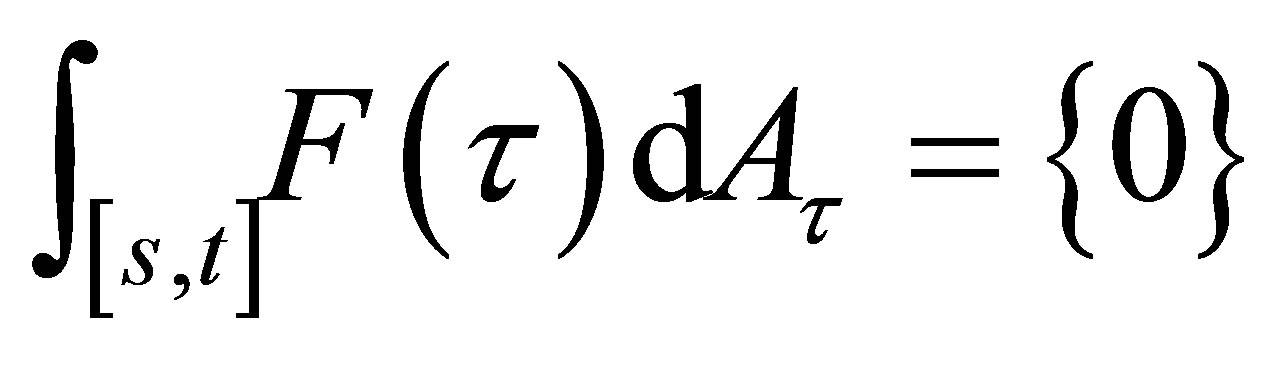, therefore it is well defined for every.

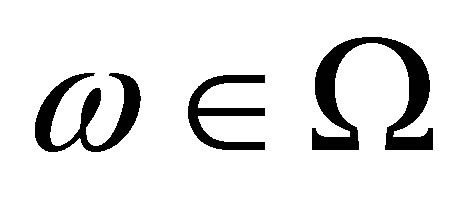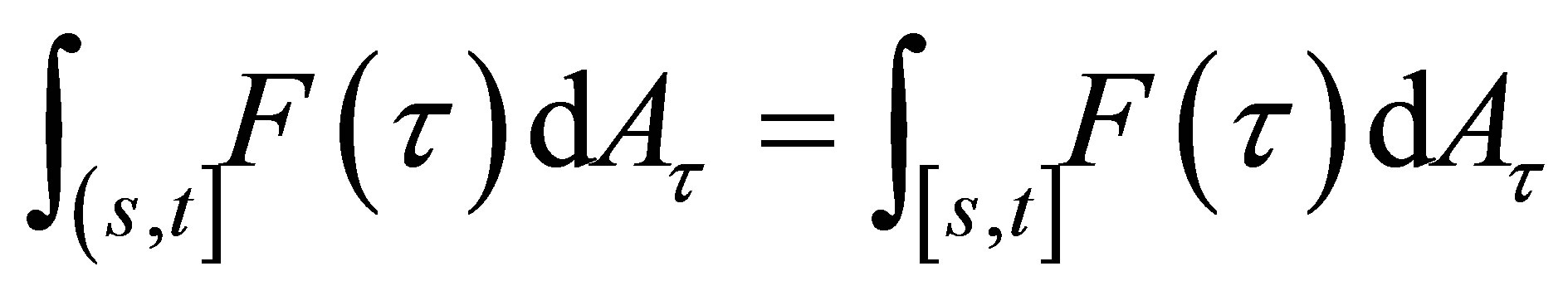since the continuity of

. In the sequel, we shall denote the integral by

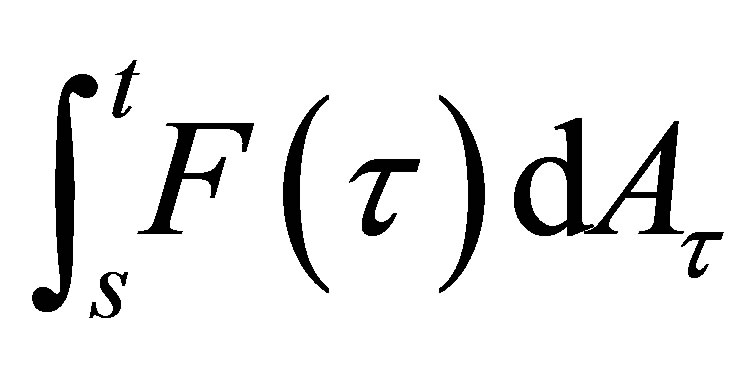instead of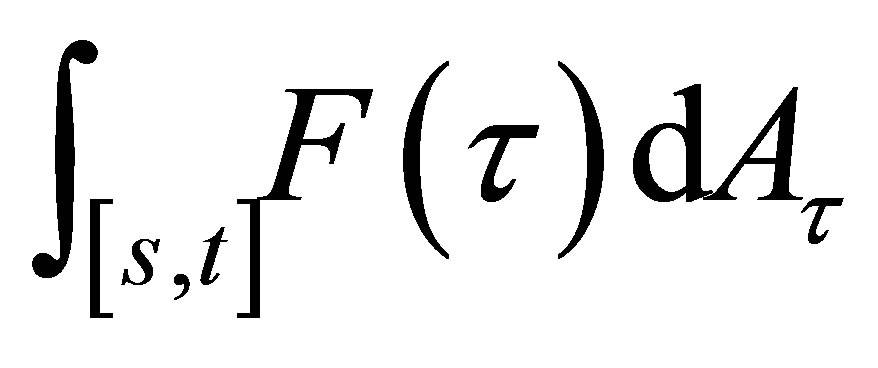. For any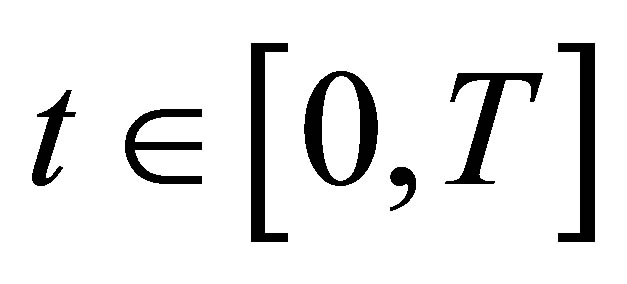denote 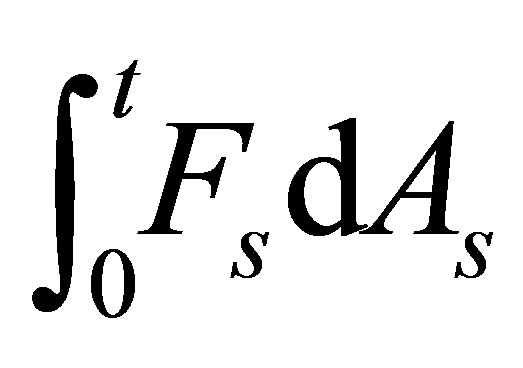by.

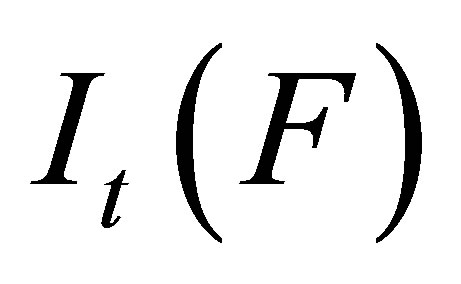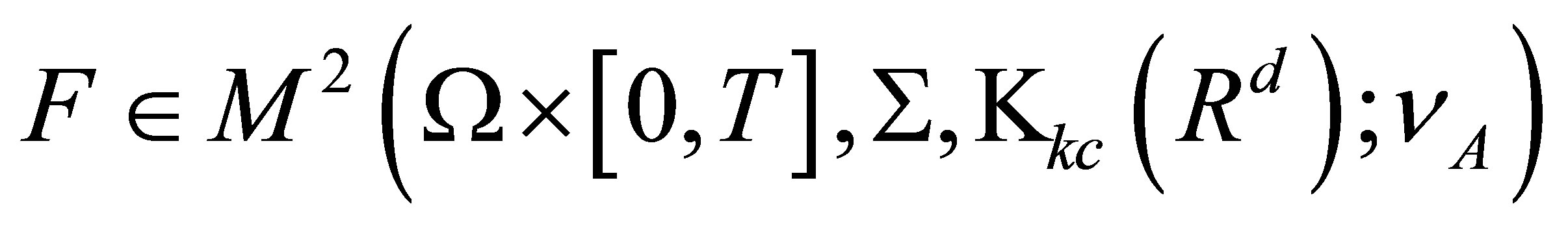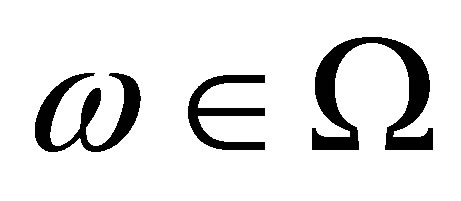Theorem 1. For, and, the Lebesgue-Stieltjes integral is a compact and convex subset of.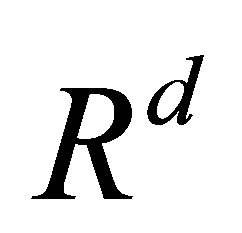

Proof 1. In fact, 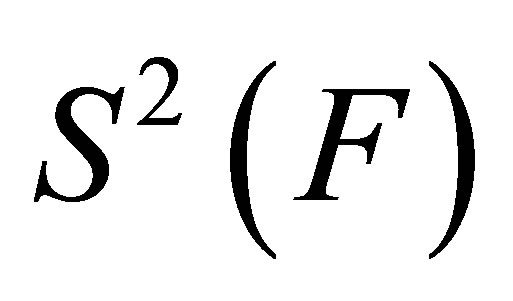is a bounded and convex subset of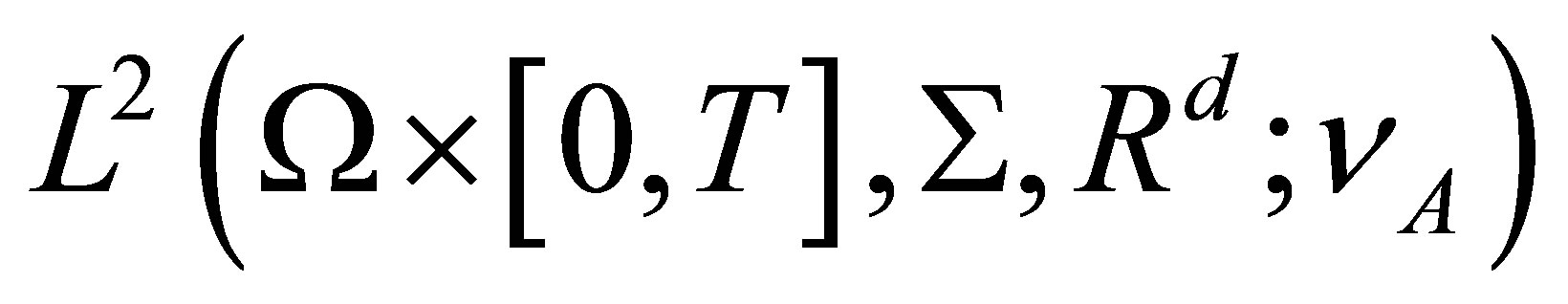, since is convex and compact,moreover, it is weakly compact since 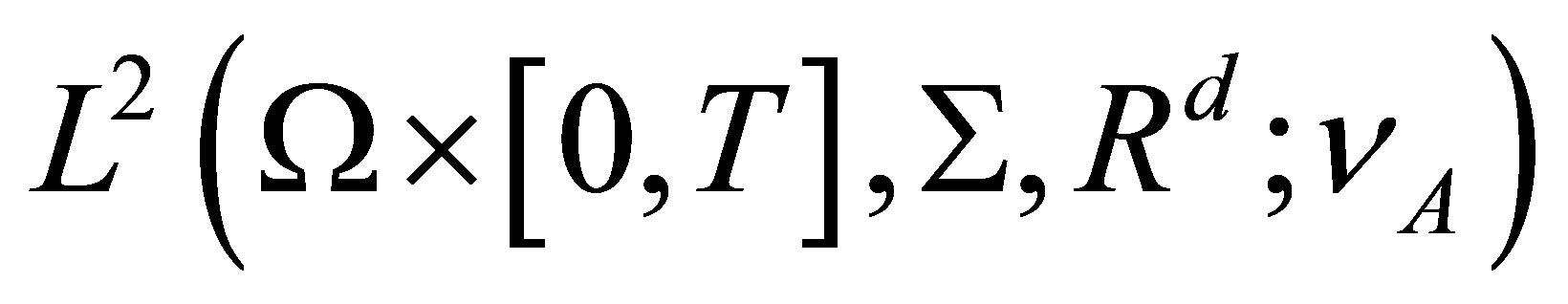is reflexive. The convexity of the integral is obvious.

We shall show the linear operator 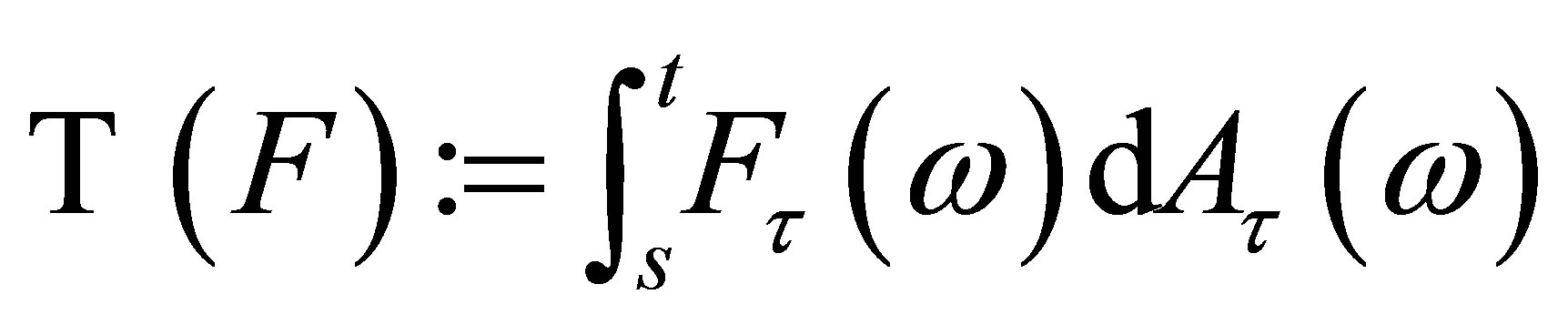: 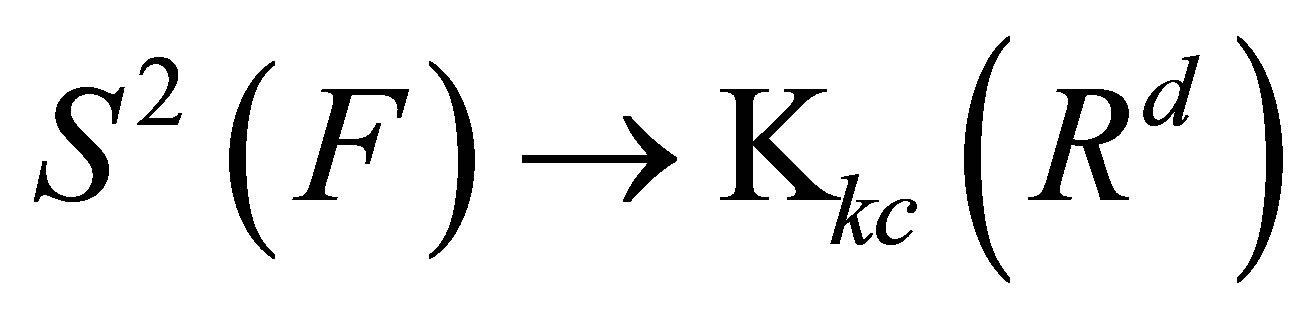is bounded.

For any, ,

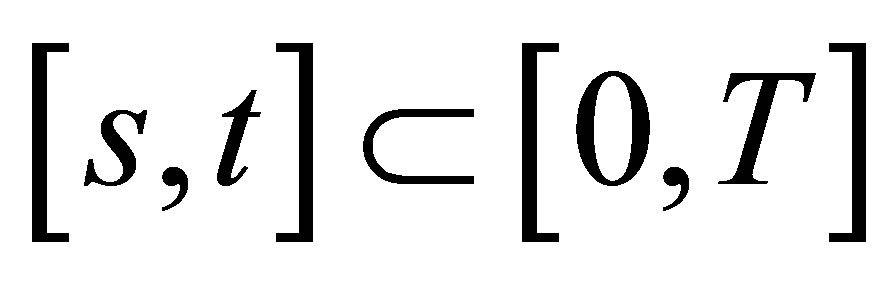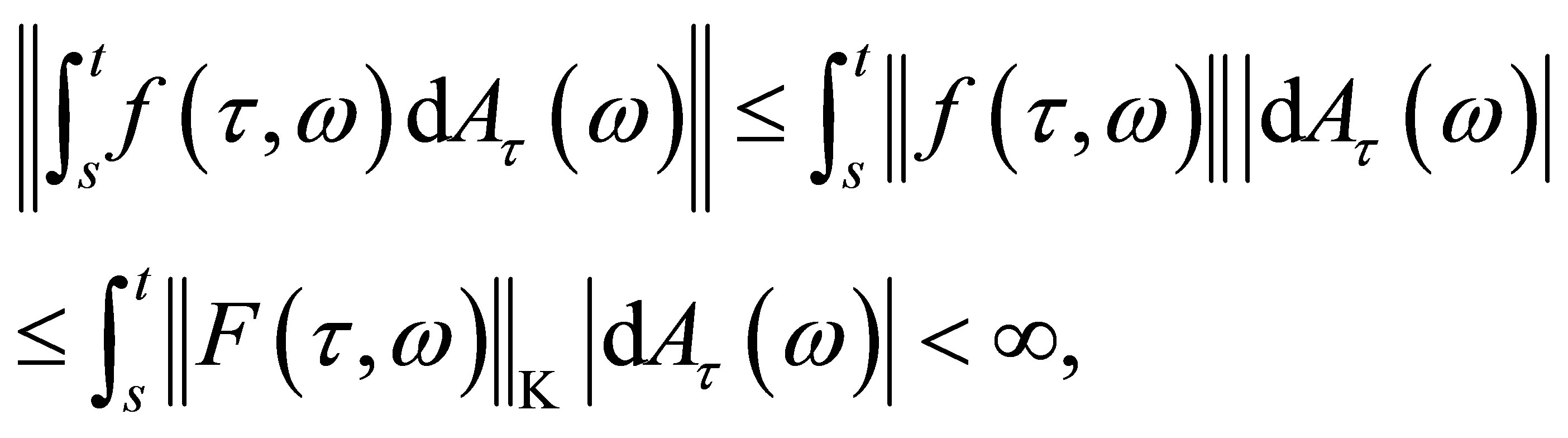(5)

which implies the linear operator is bounded. Therefore the integral 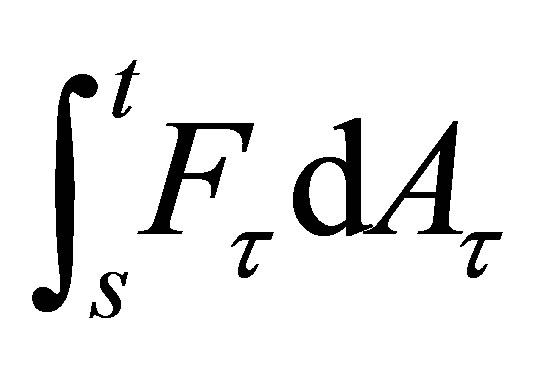is weakly compact since the bounded linear operator mapping a weakly compact set to a weakly compact one. In 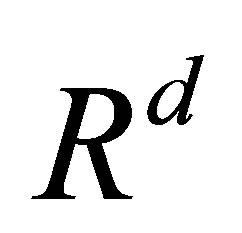space, a weakly compact set is compact.

Lemma 1. (see [16] Corollary 2.1.1 (5)) Assume is a measurable space, is a separable Banach space, 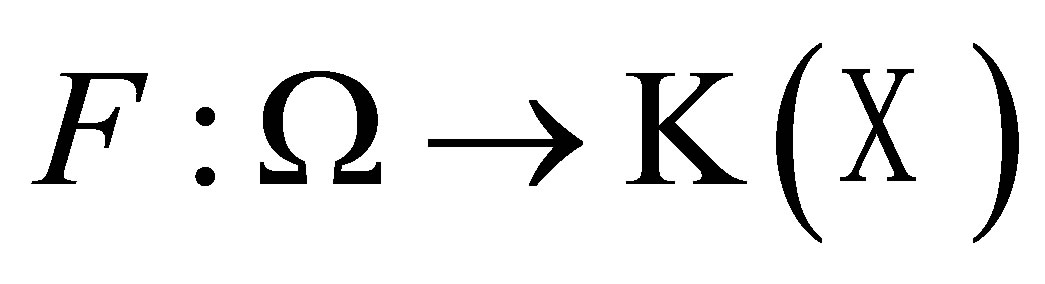, and F is a set-valued random variable, then 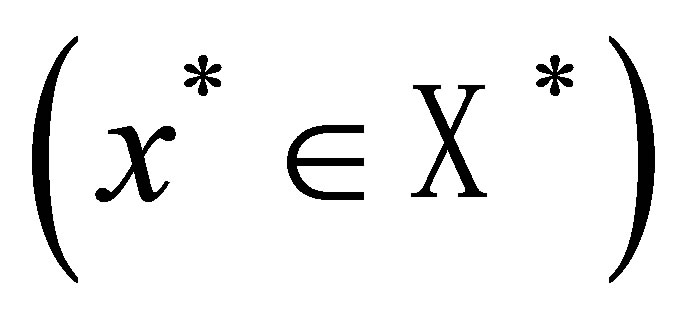is measurable.

By using Lemma 1, as a manner similar to Theorem 1 in [17], we have the following result:

Lemma 2. Assume 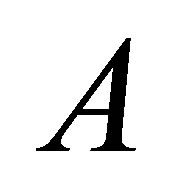is the corresponding stochastic process, 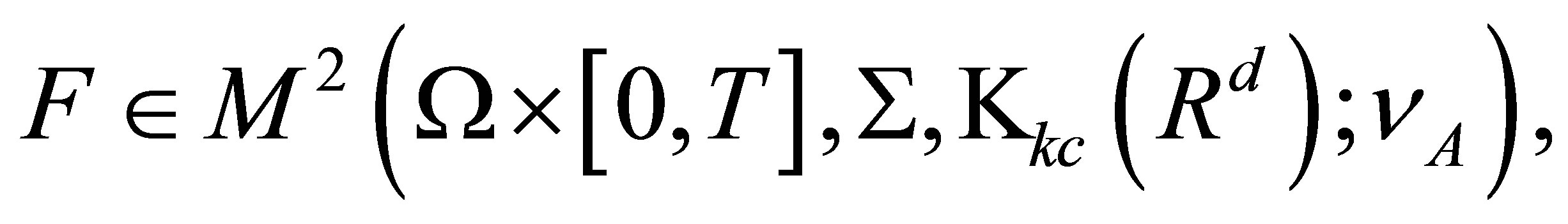for any, we have 1);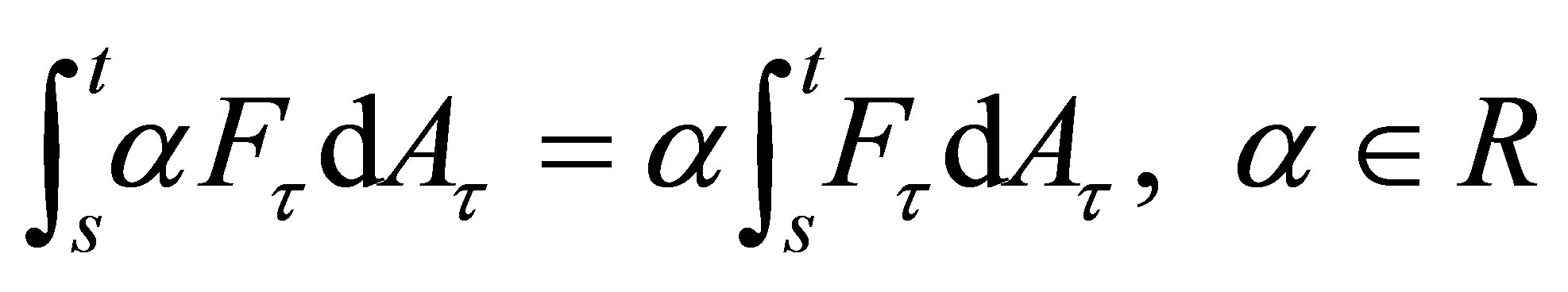

2)

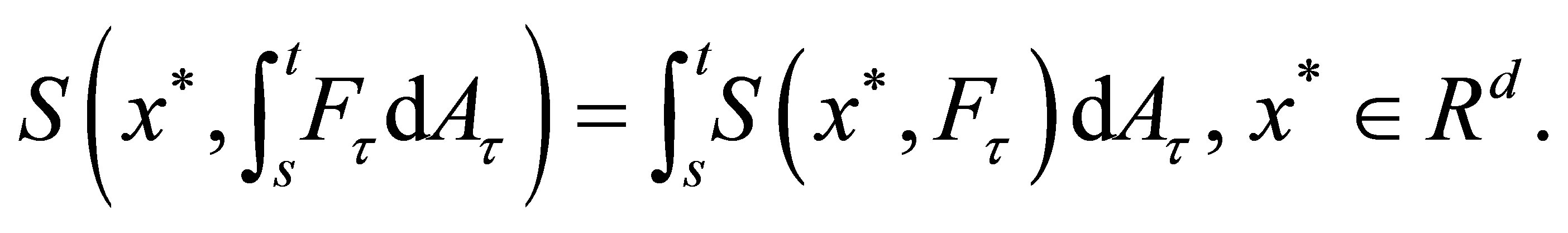
Lemma 3. (see [16] Theorem 2.1.16) Assume is a measurable space, 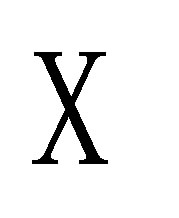is a separable Banach space, 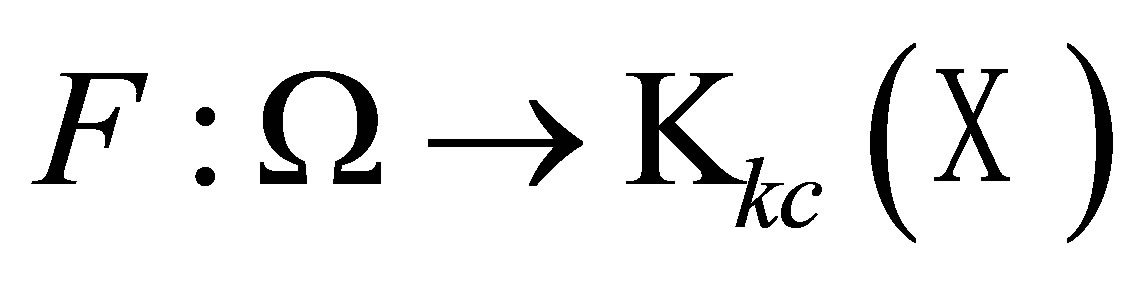, and for any fixed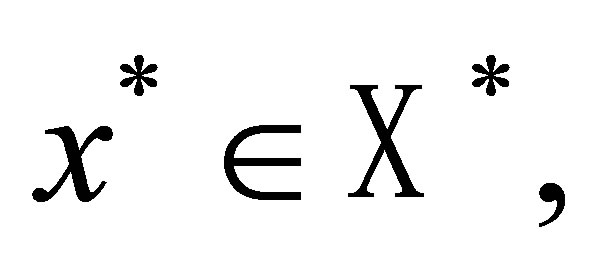 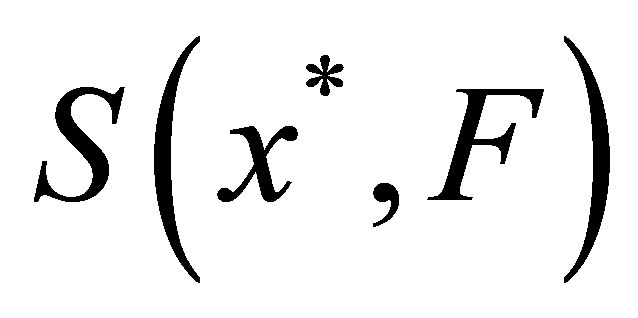is measurable, if one of the following conditions is satisfied:

1) 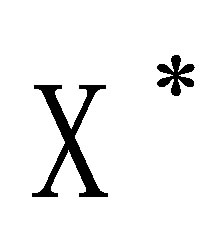is separable;

2) for any.

Then is a set-valued random variable.

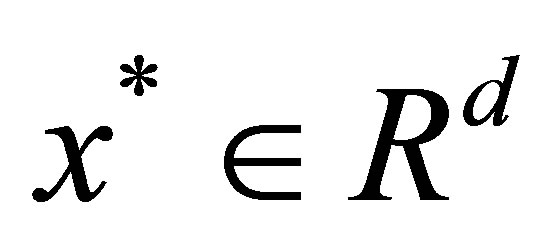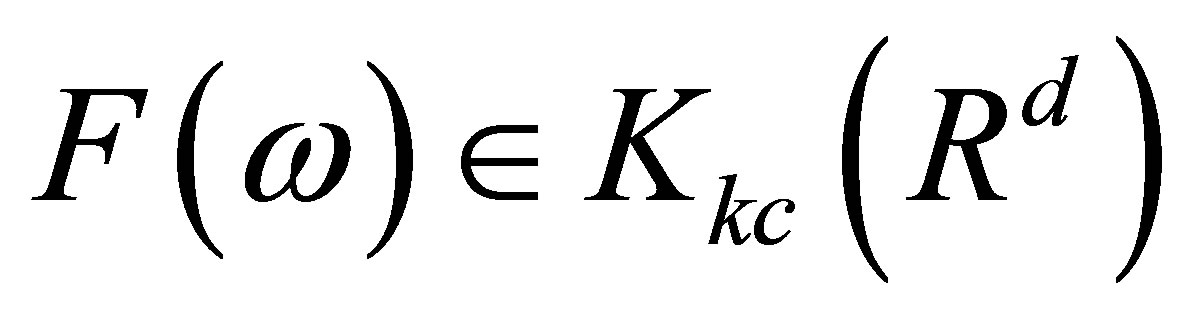From Lemma 1 and Lemma 3, when, for any, is 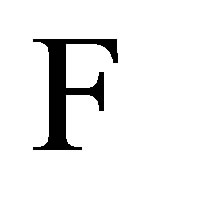-measurable if and only if 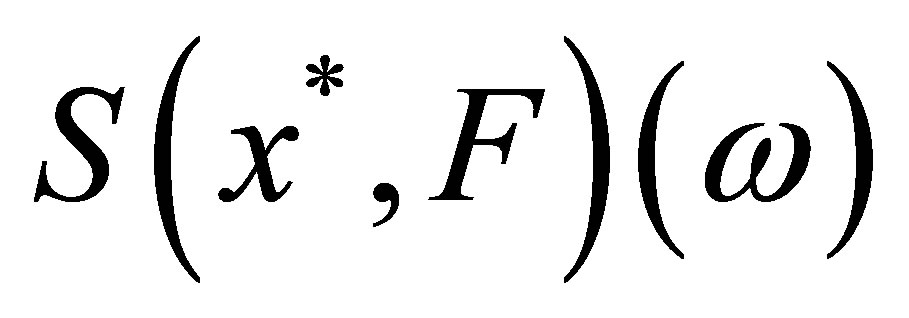is -measurable.

Lemma 4. ([16] Theorem 1.7.7) If 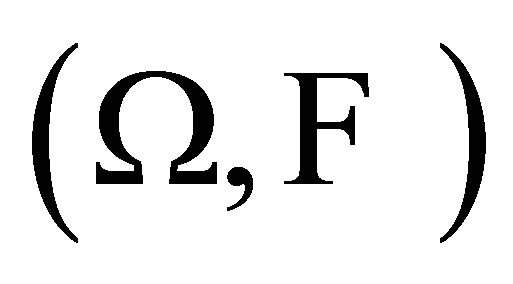is a separable space, 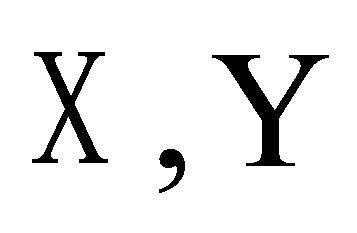are separable metric space satisfy:

(a) for any is measurable;

(b) for any 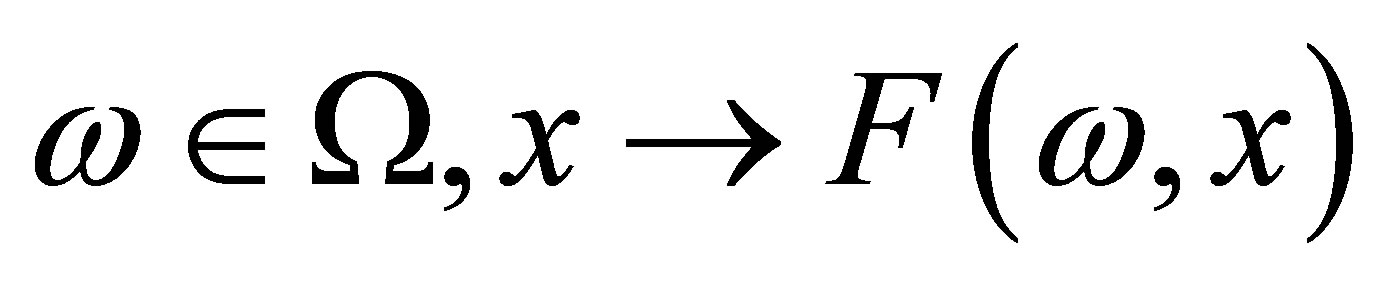is continuous or is continuous with respect to Hausdorff metricThen is jointly measurable.

Then by Lemma 1 we have the following:

Lemma 5. Assume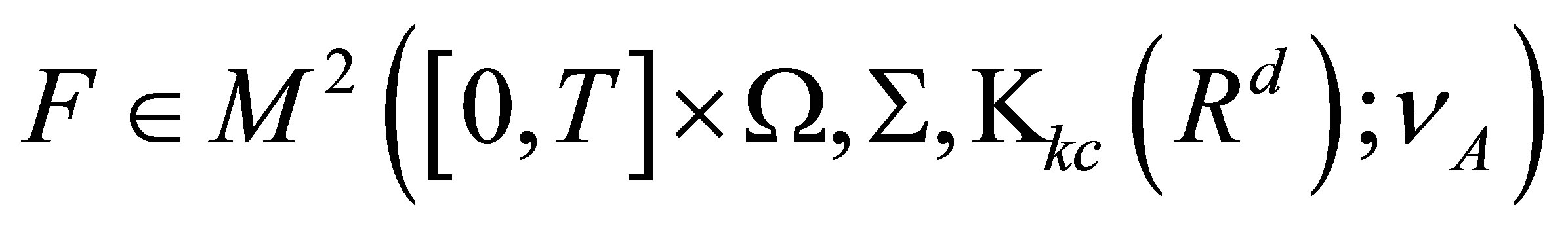. Then 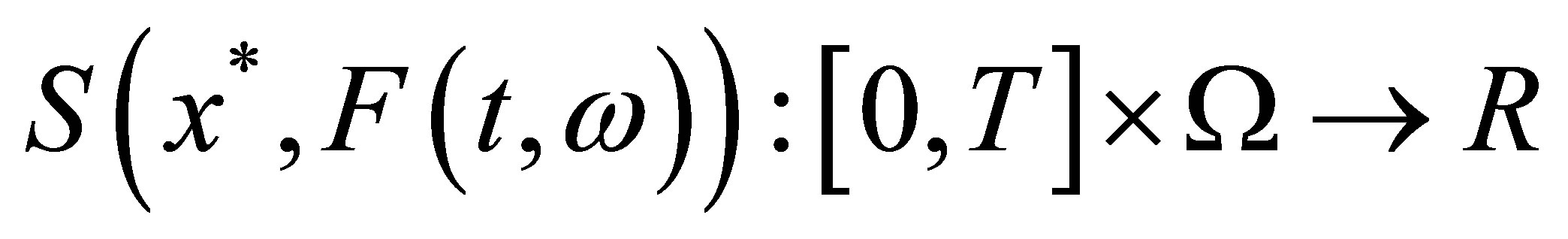is -measurable.

Theorem 2. Assume . Then for each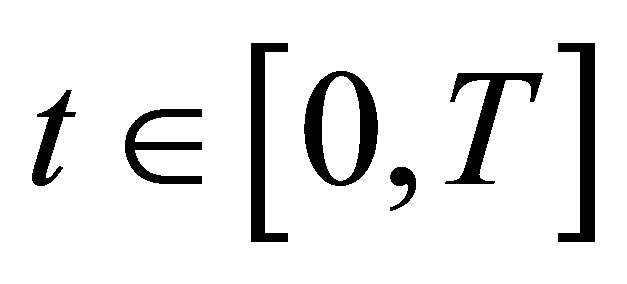. Furthermore, the mapping is -measurable.

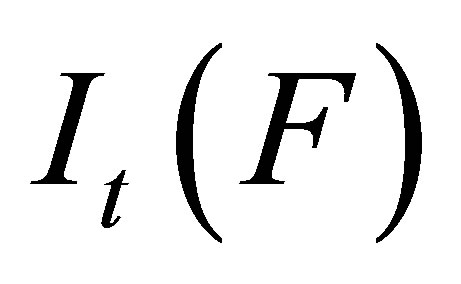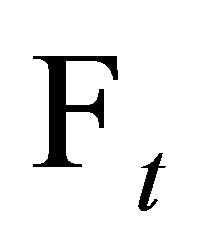Proof 2. Step 1. We will show that is - measurable for each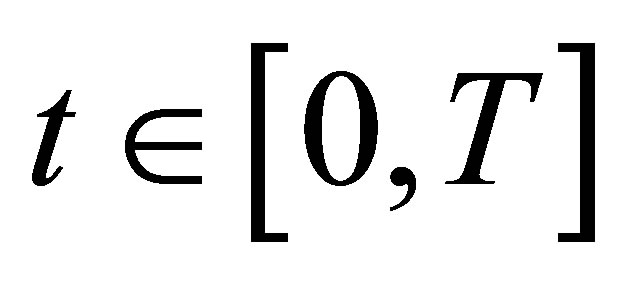, is 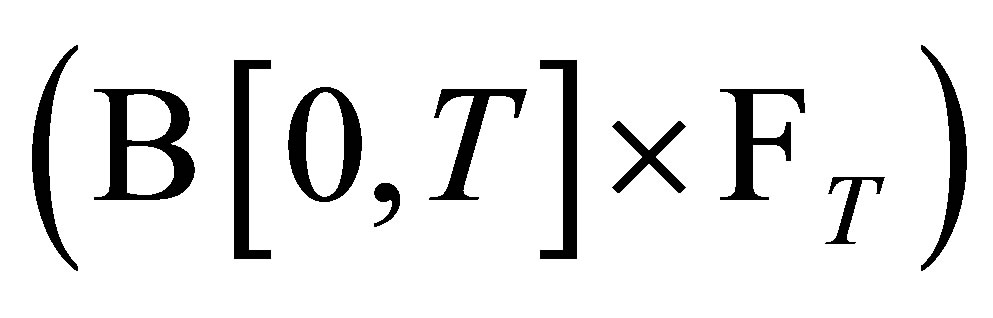-measurable.

By Theorem 1, we have

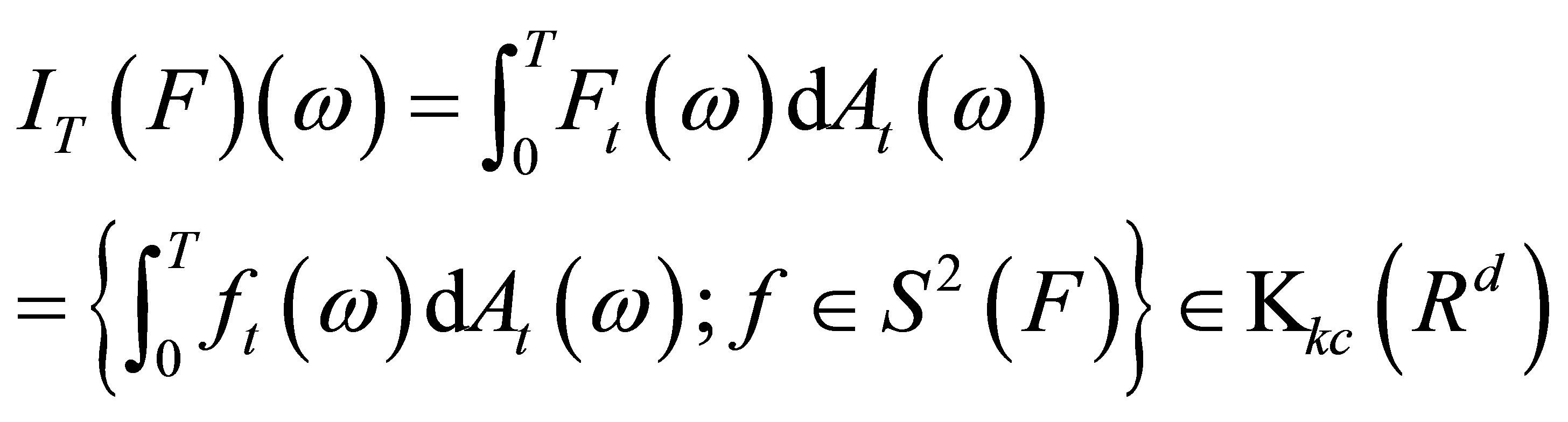(6)

for all. Furthermore, we obtain

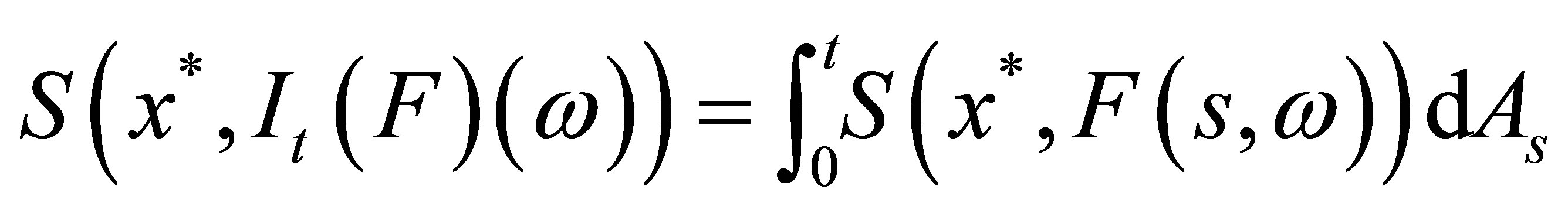
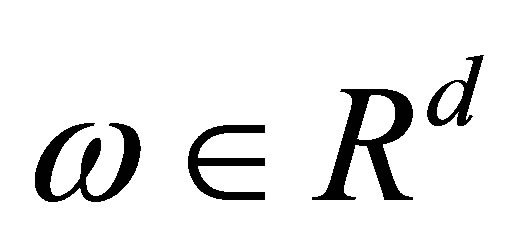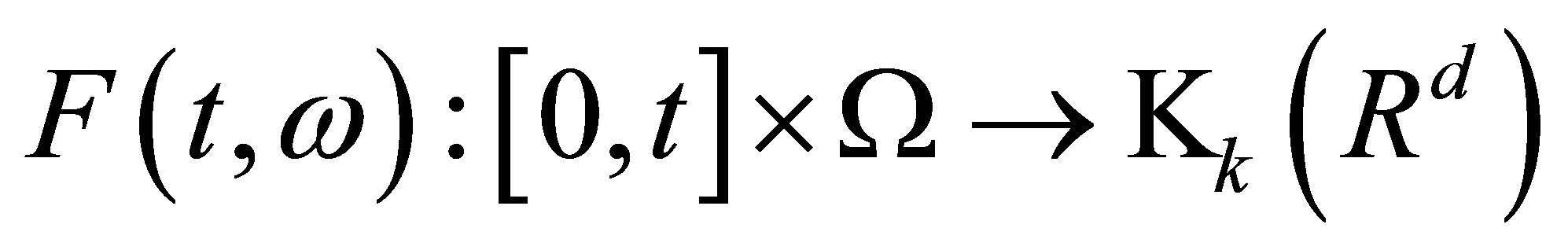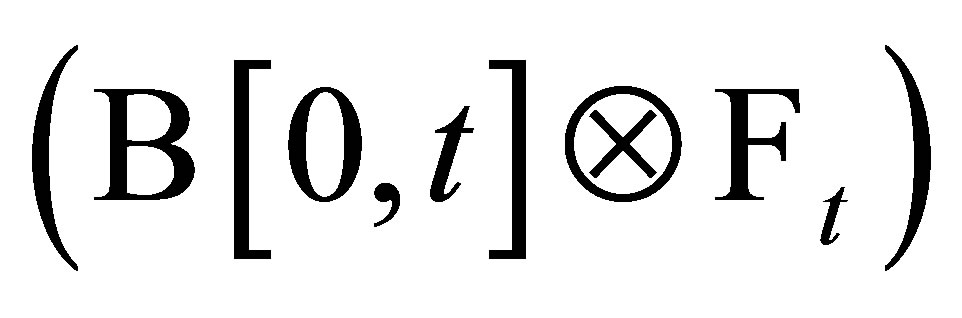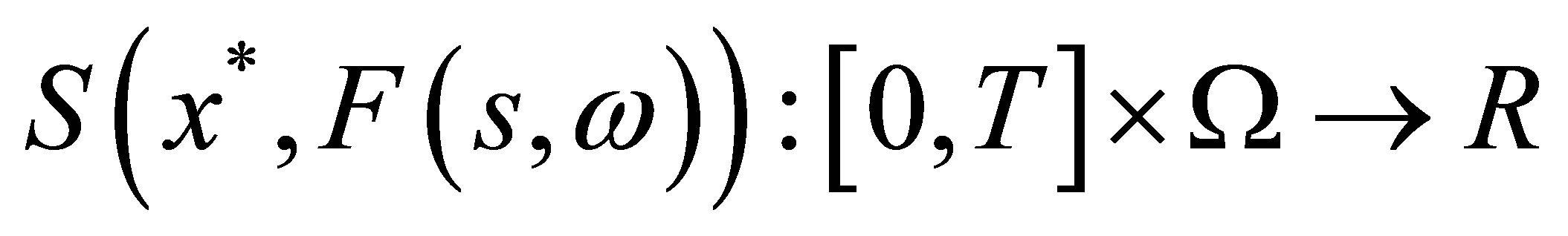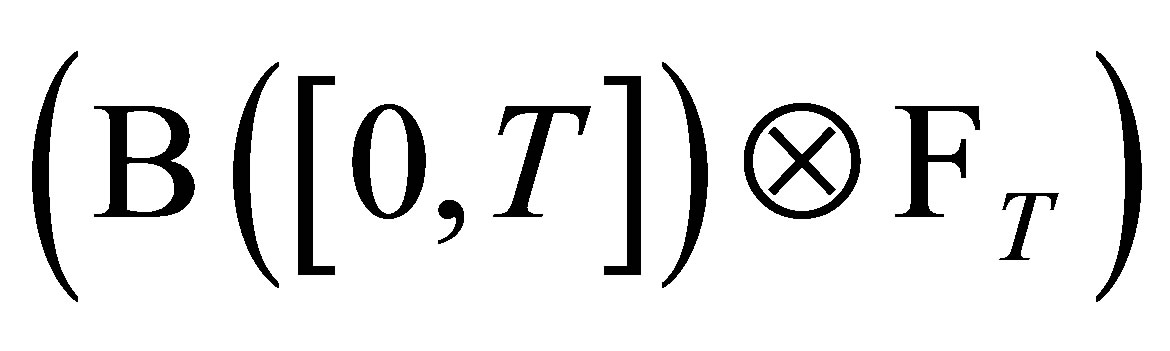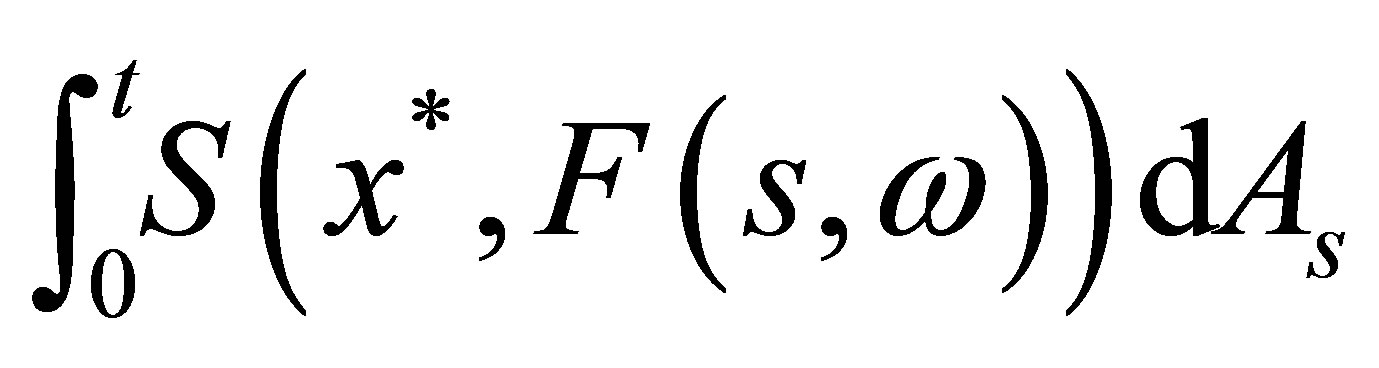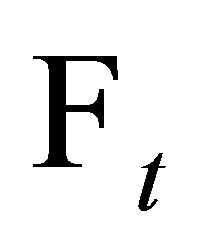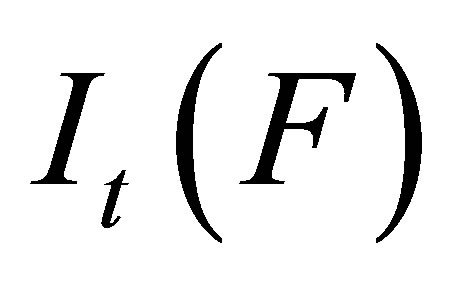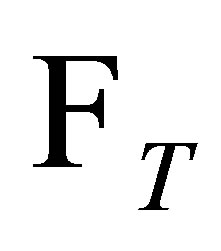for all. Moreover, since is -measurable, from the Lemma 5 we can obtain that the function is measurable. By Fubini theorem, is -measurable, based on Lemma 3, is -measurable.

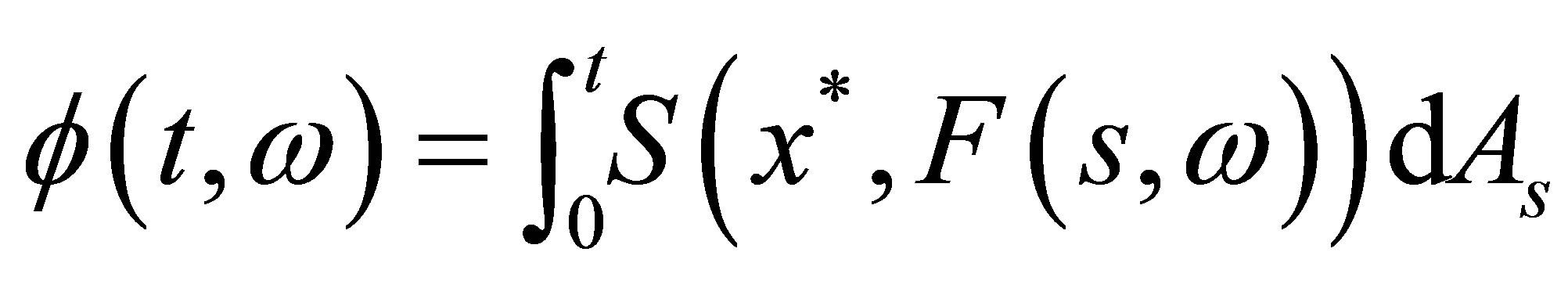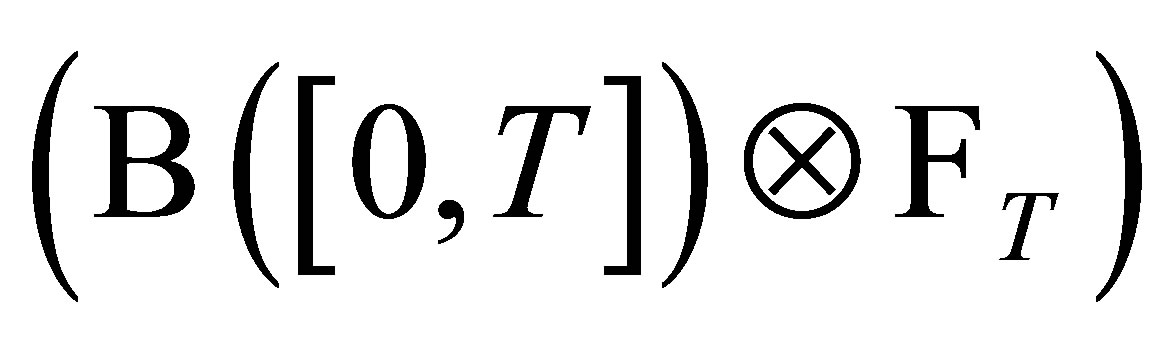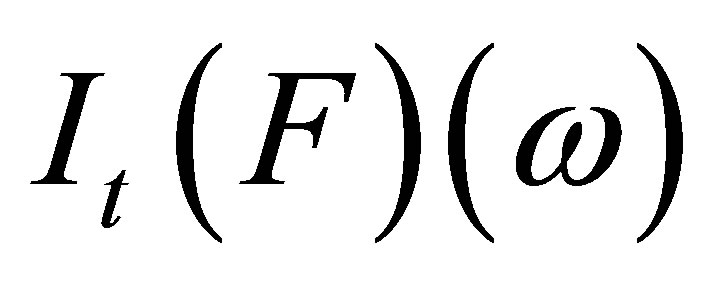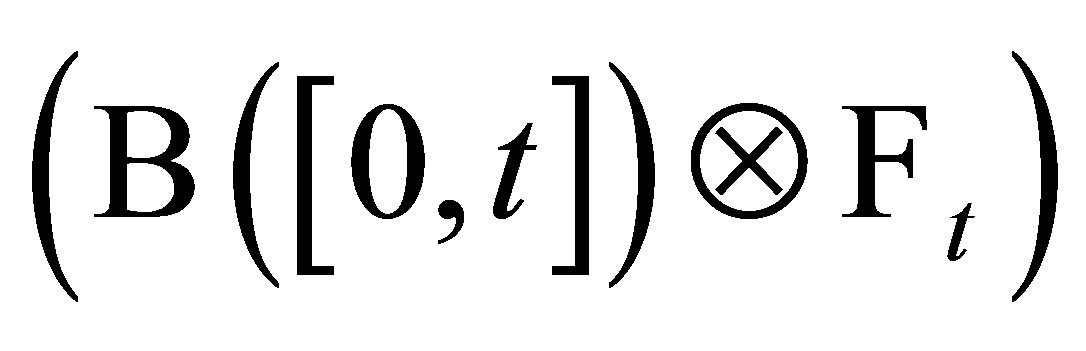Finally, in the argument above, the function is -measurable for each. Since it is continuous in for all, so it is -measurable. From Lemma 4, we obtain that is - measurable.

Step 2. In this step, we will show that 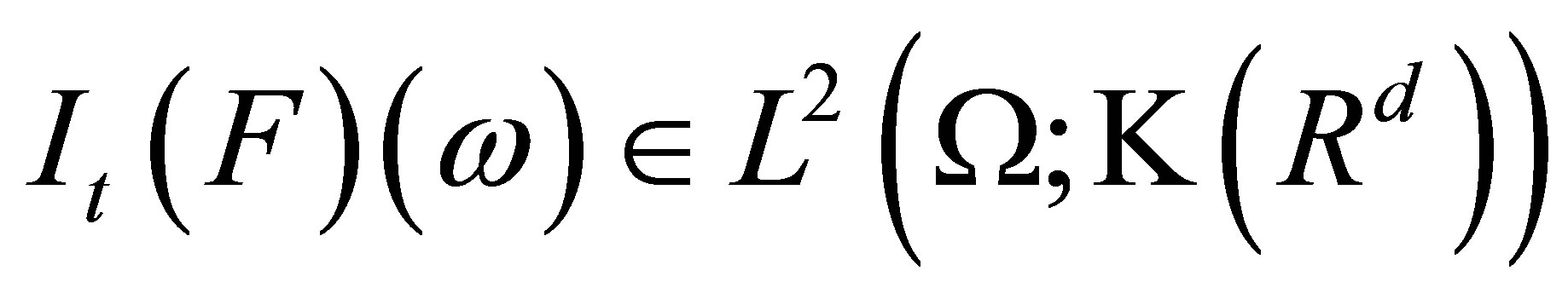for each.

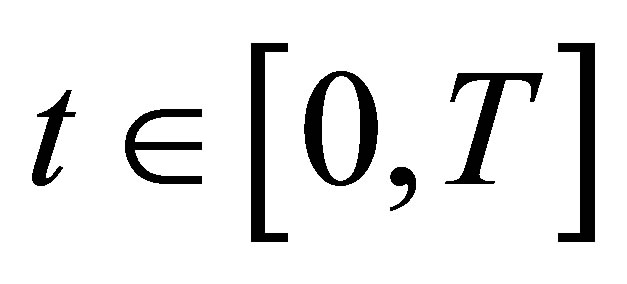For each and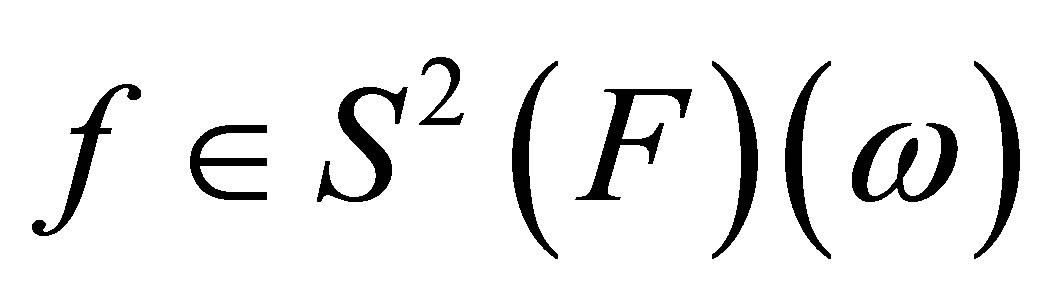, we have

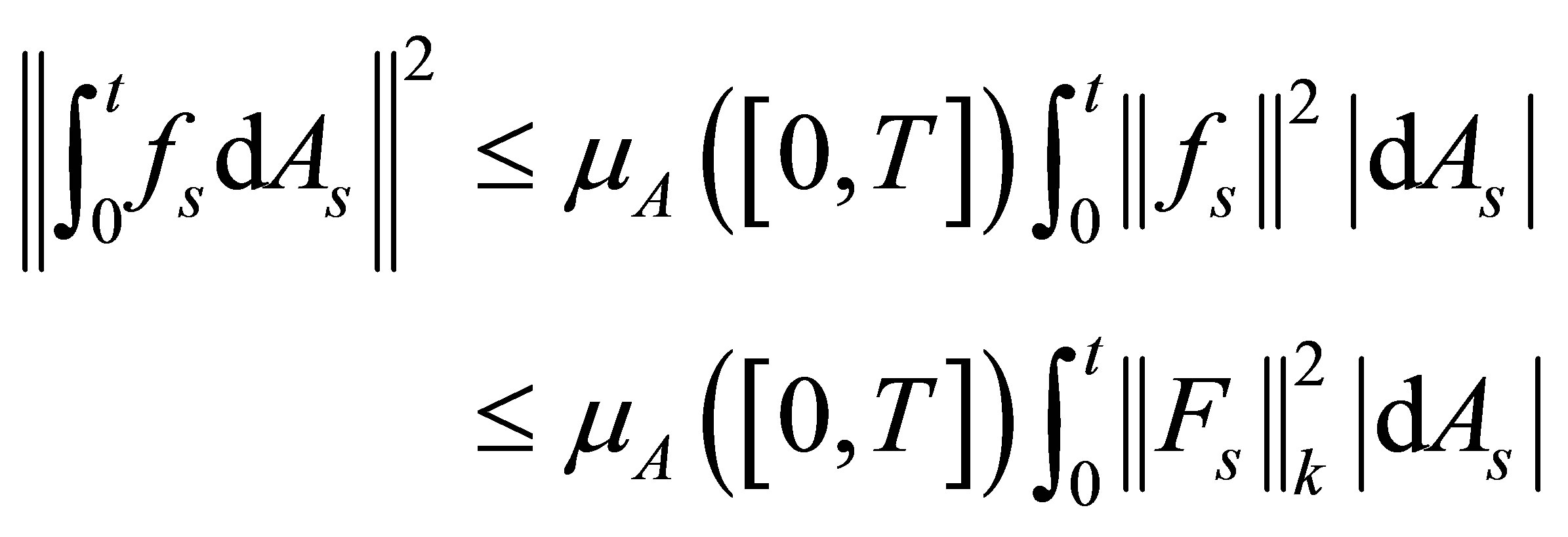(7)

then

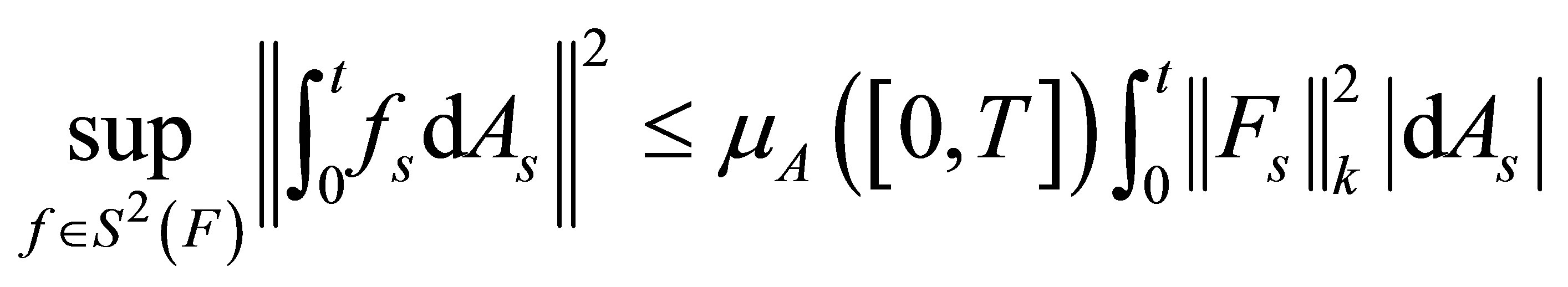
Hence,

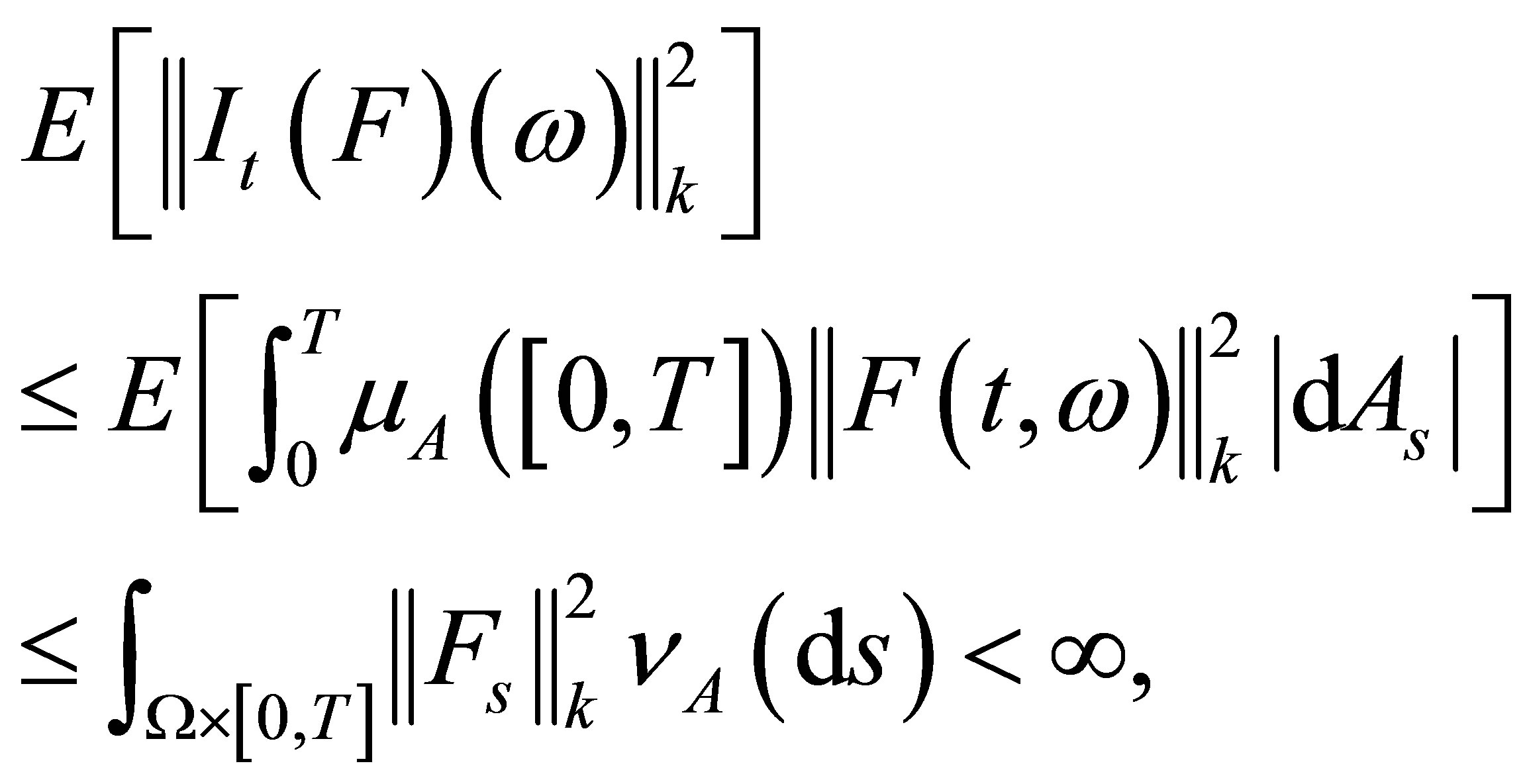(8)

which implies

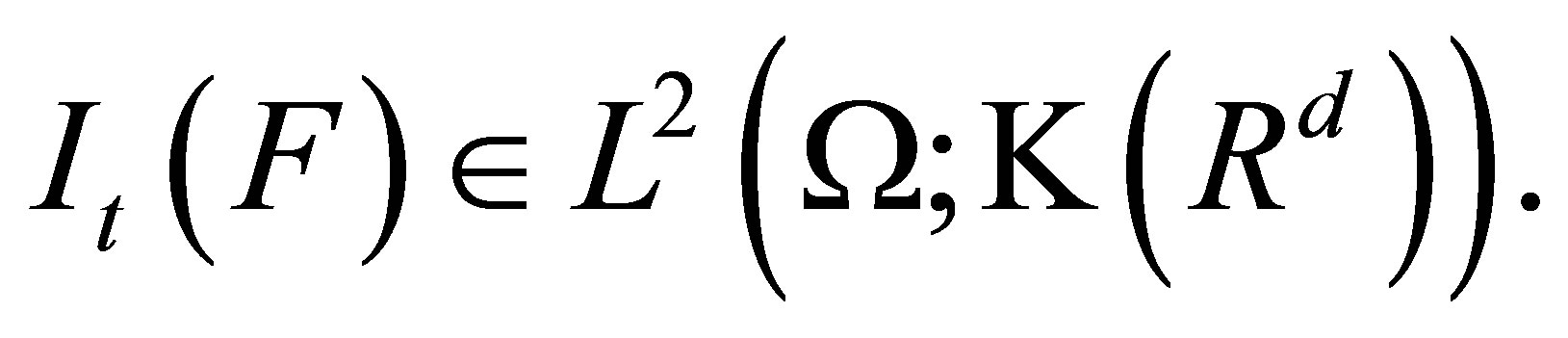
As a manner similar to Theorem 3.8. in [8], we have the Castaing representation as following:

Theorem 3. For a set-valued stochastic process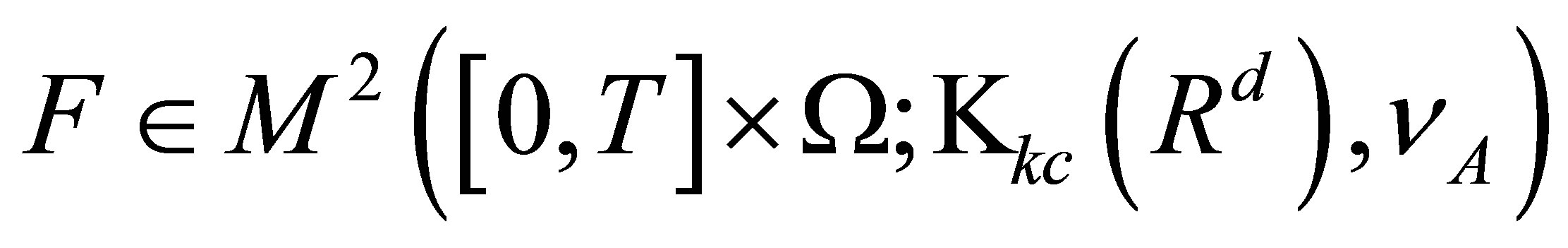, there exists a sequence 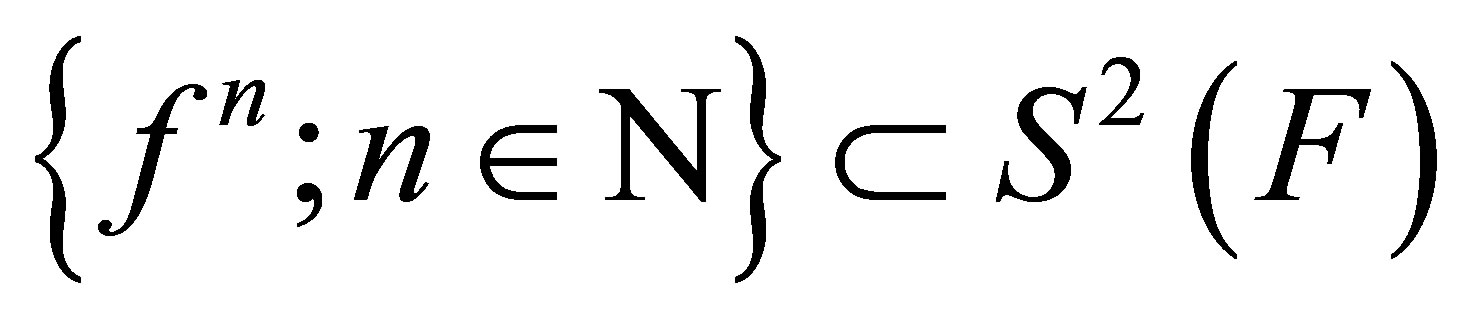such that

and, for,

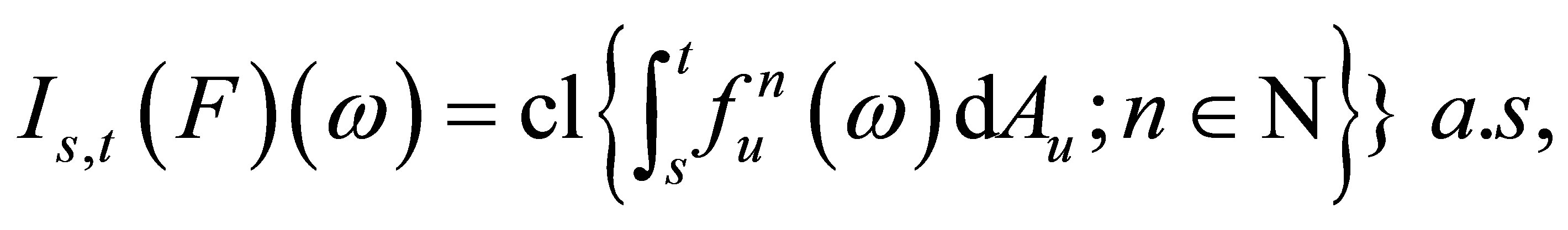
where cl denotes the closure in.

Theorem 4. For each 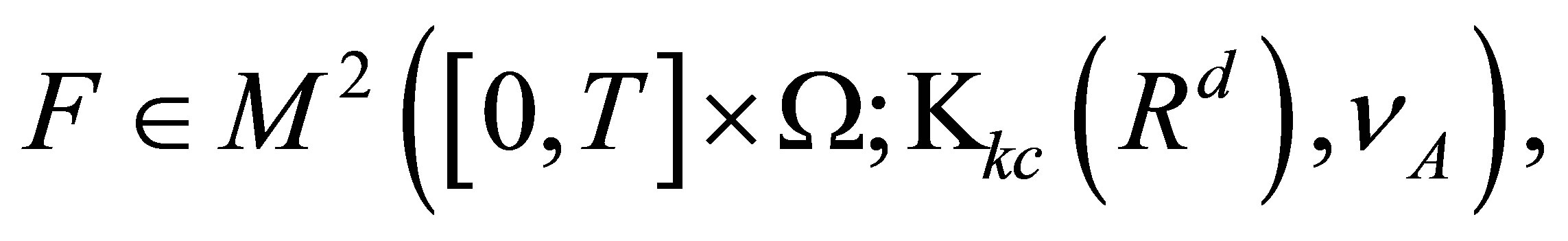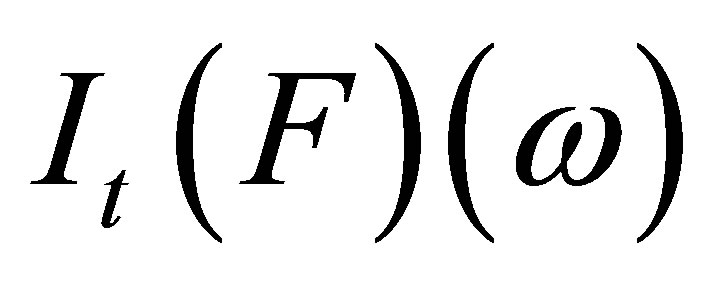is continuous a.s. with respect to the Hausdorff metric.

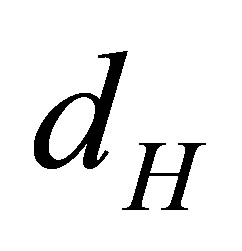Proof 3. Let 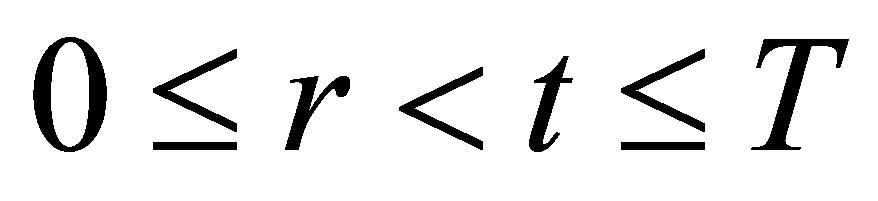and. We then have

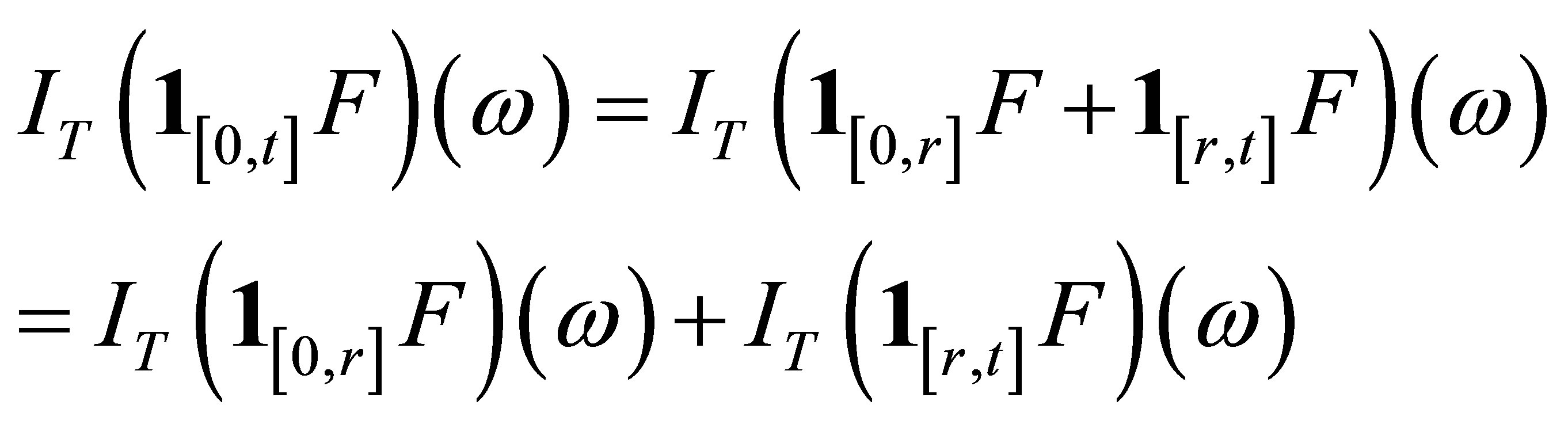(9)

Hence,

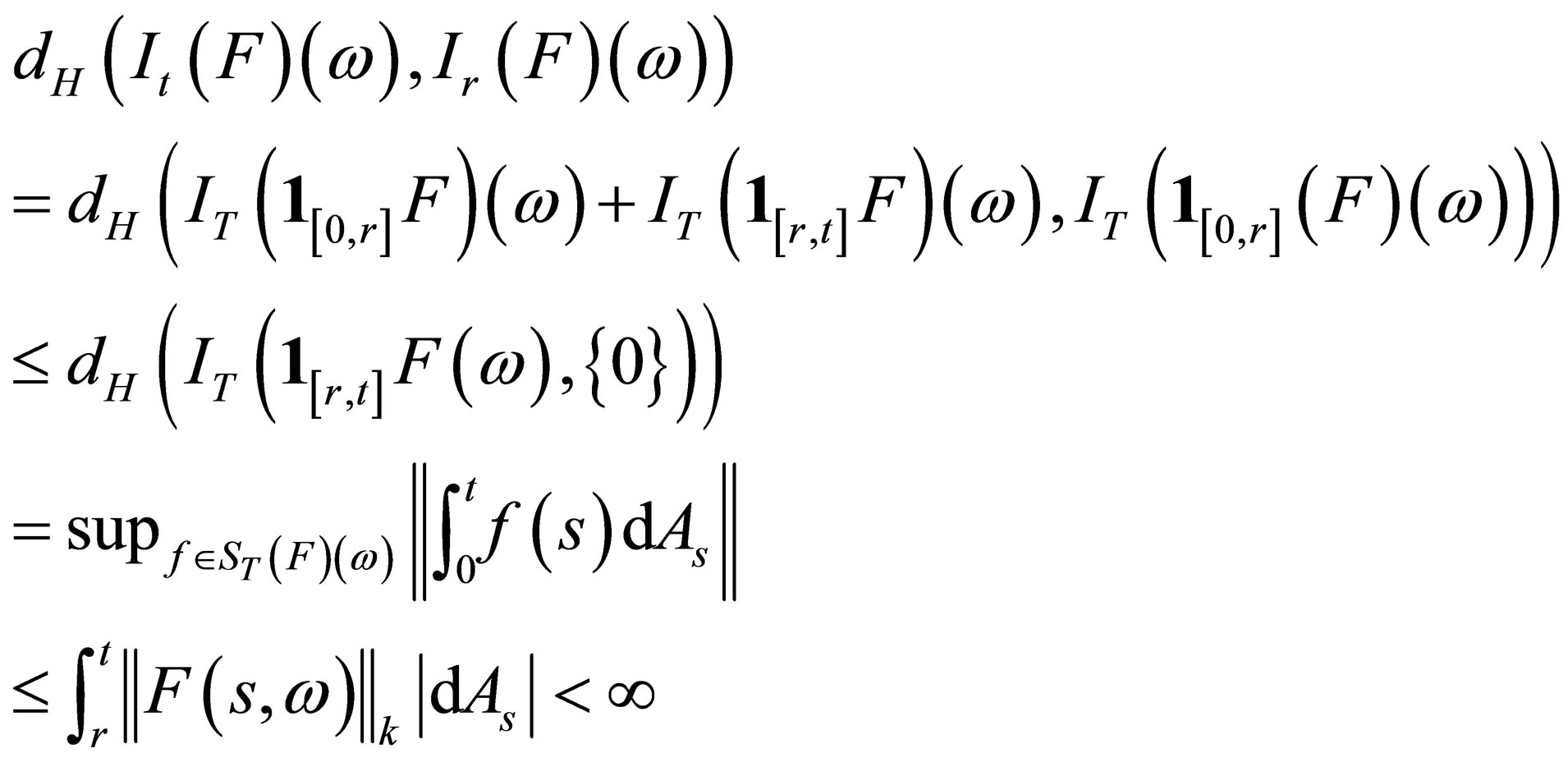
(10)

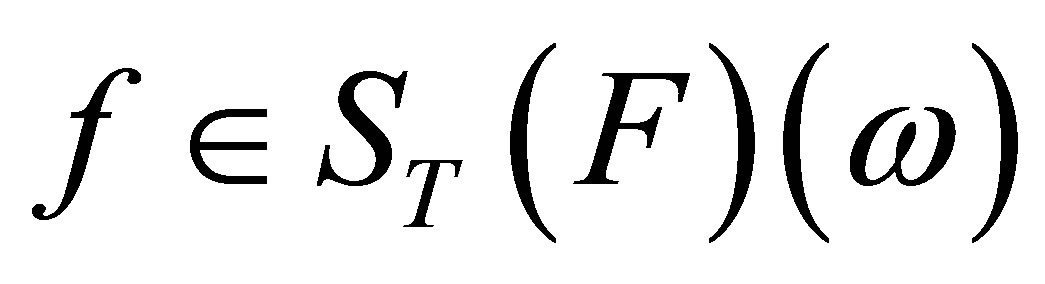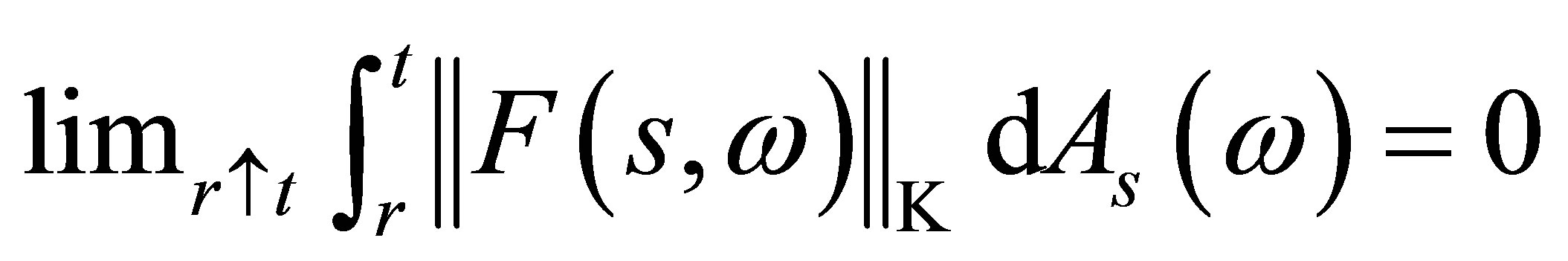since for each,. Hence,. So 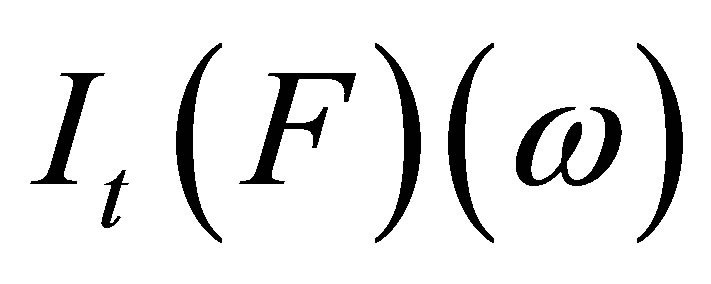is leftcontinuous in 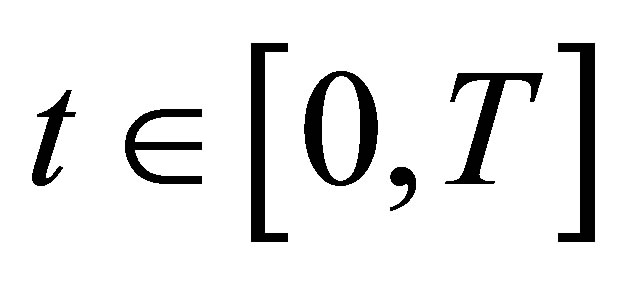for all a.s. In a similar way, we see that 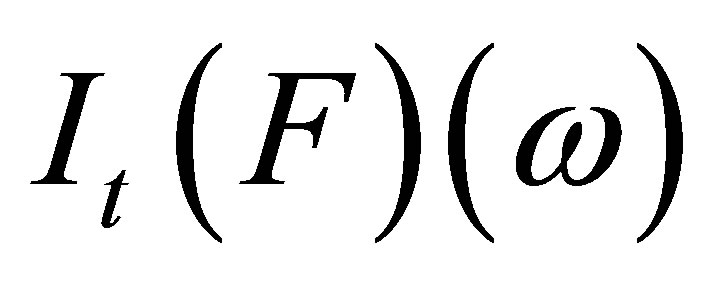is right-continuous in 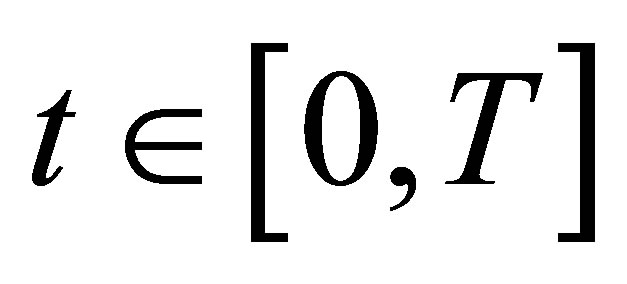a.s.

Similar to the proof of Theorem 3.15 in [8], we have the following theorem:

Theorem 5. Let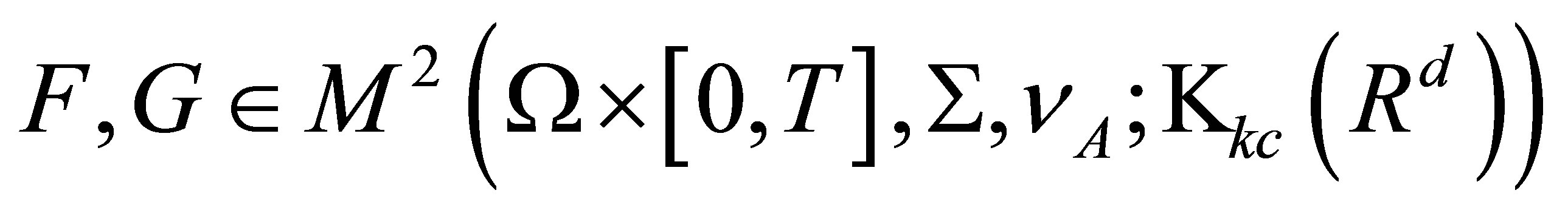, for any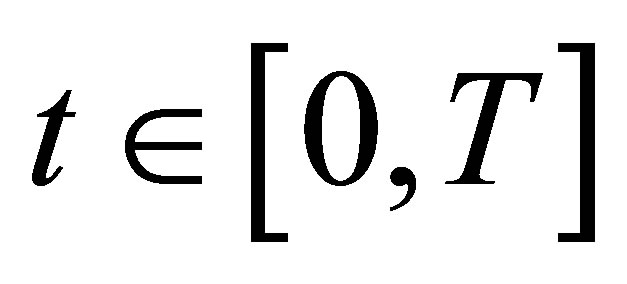, we have

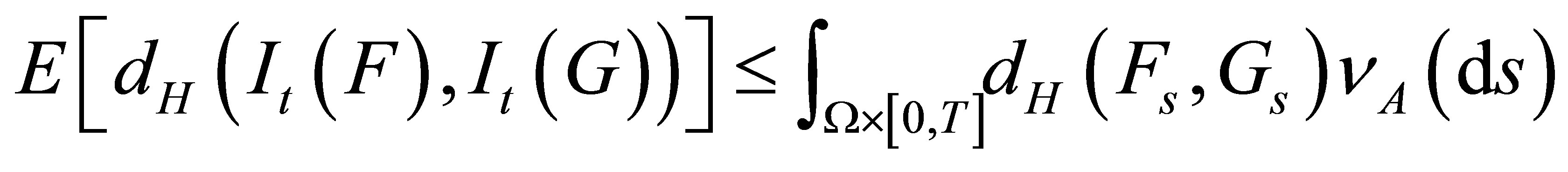
and

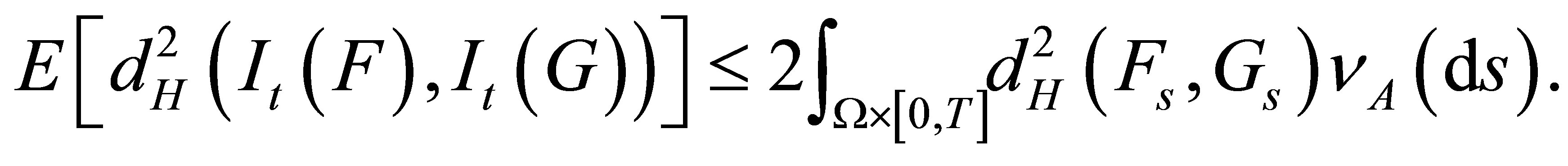
4. Conclusion

When the integrand takes values in compact and convex subsets of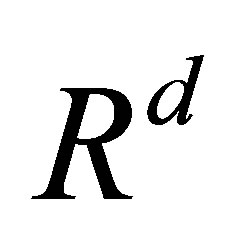, we defined the integral with respect to real-valued variation processes. And then we proved some properties of this kind of integral such as measurability, 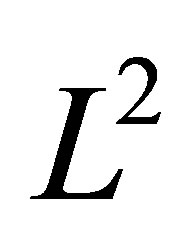-boundedness and continuity under the Hausdorff metric.

5. Acknowledgements

We would like to thank the referees for their valuable comments. Moreover, we express special thanks to our editor of the journal APM for his(her) efficiency and support.

REFERENCES

NOTES

^*This work is partly supported by The Co-Construction Project of Beijing Municipal Commission of Education, The Project Sponsored by SRF for ROCS, SEM and The Fundamental Research Funds for the Central Universities, No 12MS81.

^#Corresponding author.