Advances in Pure Mathematics
Vol.3 No.7(2013), Article ID:38116,4 pages DOI:10.4236/apm.2013.37080
Variation of the Spectrum of Operators in Infinite Dimensional Spaces
Department of Mathematics and Computer Science, Ursinus College, Collegeville, USA
Email: myahdi@ursinus.edu
Copyright © 2013 Mohammed Yahdi. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received July 25, 2013; revised August 26, 2013; accepted September 29, 2013
Keywords: Operator Spectrum; Borel Function; Banach Space; Polish Space
ABSTRACT
The paper investigates the variation of the spectrum of operators in infinite dimensional Banach spaces. Consider the space of bounded operators on a separable Banach space when equipped with the strong operator topology, and the Polish space of compact subsets of the closed unit disc of the complex plane when equipped with the Hausdorff topology. Then, it is shown that the unit spectrum function is Borel from the space of bounded operators into the Polish space of compact subsets of the closed unit disc. Alternative results are given when other topologies are used.
1. Introduction
Let 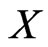 be an infinite dimensional Banach space. We denote by
be an infinite dimensional Banach space. We denote by 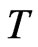 an arbitrary bounded operator on
an arbitrary bounded operator on 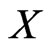 and by
and by 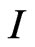 the identity operator on
the identity operator on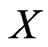 . Let
. Let 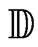 be the closed unit disc of the complex plane
be the closed unit disc of the complex plane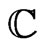 . The restriction on
. The restriction on 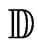 of the spectrum of an operator
of the spectrum of an operator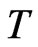 , denoted by
, denoted by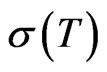 , is the unit spectrum defined as follows:
, is the unit spectrum defined as follows:
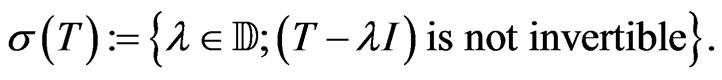
Essential spectra of some matrix operators on Banach spaces (see [1]) and spectra of some block operator matrices (see [2]) were investigated, with applications to differential and transport operators. This paper investigates the variations of the unit spectrum 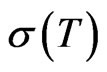 as
as 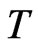 varies over the space
varies over the space 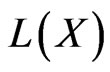 of all bounded operator on the Banach space
of all bounded operator on the Banach space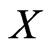 . First, we introduce the sets and the topologies required for this study.
. First, we introduce the sets and the topologies required for this study.
Definition 1
• 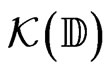 the set of all compact subsets of the closed unit disc
the set of all compact subsets of the closed unit disc 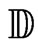 of the complex plane
of the complex plane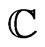 ;
;
• 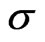 the spectrum function defined from
the spectrum function defined from 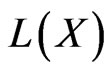 into
into 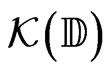 that maps an operator
that maps an operator 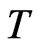 to its unit spectrum
to its unit spectrum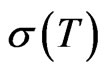 .
.
The set 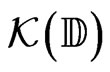 is endowed with the Hausdorff topology generated by the families of all subsets in one of the following forms
is endowed with the Hausdorff topology generated by the families of all subsets in one of the following forms
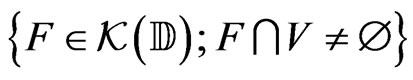
and
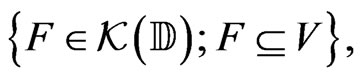
for 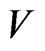 an open subset of
an open subset of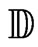 . Therefore,
. Therefore, 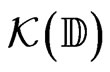 is a Polish space, i.e., a separable metrizable complete space, since
is a Polish space, i.e., a separable metrizable complete space, since 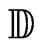 is Polish (see [3-5]). It is shown below that we can reduce the families that generate the above Hausdorff topology.
is Polish (see [3-5]). It is shown below that we can reduce the families that generate the above Hausdorff topology.
Proposition 1 Let 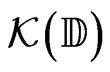 be the set of compact subsets of the closed unit disc
be the set of compact subsets of the closed unit disc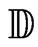 . Then
. Then 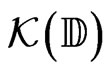 equipped with the Hausdorff topology is a Polish space; where the Borel structure is generated by one of the following two families
equipped with the Hausdorff topology is a Polish space; where the Borel structure is generated by one of the following two families
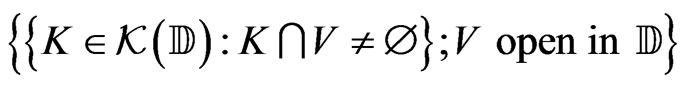
and
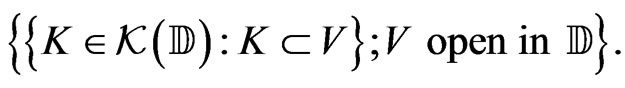
Proof 1 Let 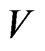 be an open subset of
be an open subset of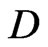 . There exists a decreasing sequence of open subsets
. There exists a decreasing sequence of open subsets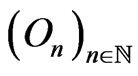 ; for example
; for example
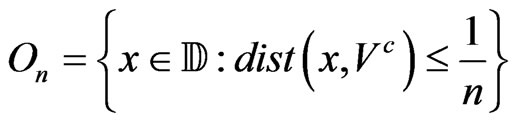 such that
such that
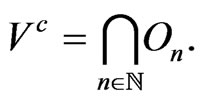
We have
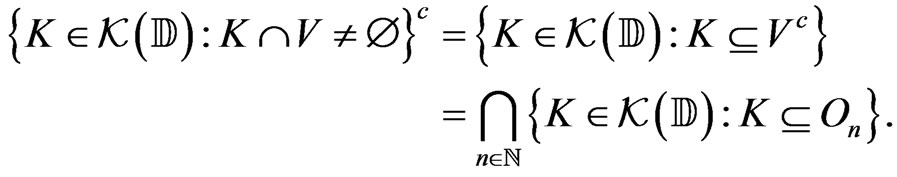
On the other hand,
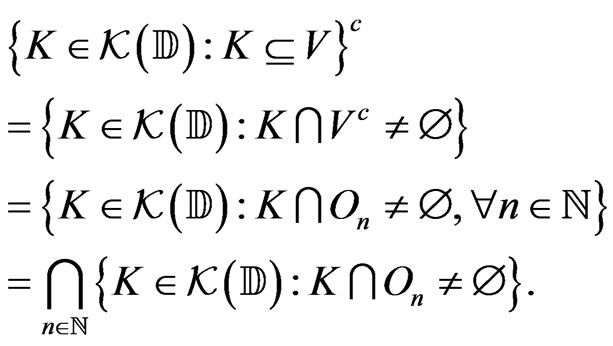
Indeed, if for all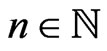 , there exists
, there exists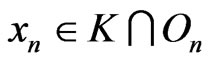 , then there exists a subsequence
, then there exists a subsequence 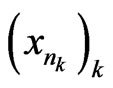 of
of 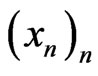 that converges to
that converges to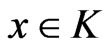 , and since
, and since 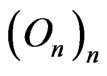 is decreasing, we have
is decreasing, we have
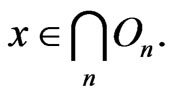
2. Norm Operator Topology and the Spectrum Function
We equip 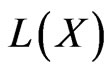 with the canonical norm of operators defined by
with the canonical norm of operators defined by
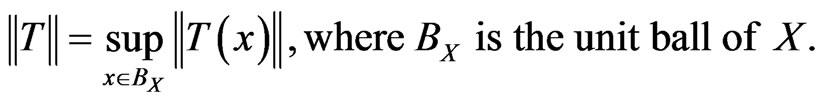
Note that the map 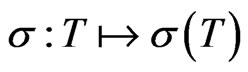 is not continuous when
is not continuous when 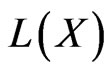 is endowed with its canonical norm.
is endowed with its canonical norm.
Indeed, the operators 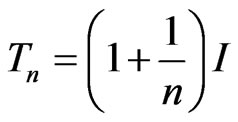 converge to the identity
converge to the identity 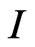 while
while 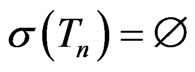 and
and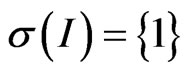 . However, we have the following result.
. However, we have the following result.
Proposition 2 Let X be a Banach space, 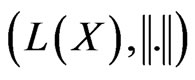 the space of bounded operators equipped with the norm of operators, and
the space of bounded operators equipped with the norm of operators, and 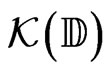 the set of compact subsets of the unit disc
the set of compact subsets of the unit disc 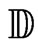 equipped with the Hausdorff topology. Then the spectrum map
equipped with the Hausdorff topology. Then the spectrum map
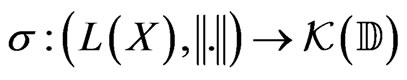
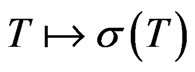
is upper-semi continuous.
Proof 2 Let  be an open subset of
be an open subset of . By proposition 1, it is only needed to show that the set
. By proposition 1, it is only needed to show that the set
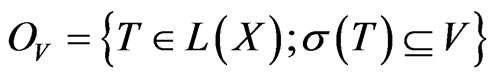
is 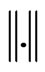 -open in
-open in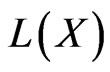 . Let
. Let 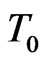 be fixed in
be fixed in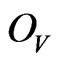 . Since
. Since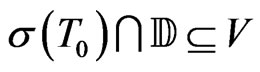 , then for all
, then for all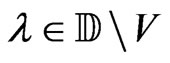
• The operator 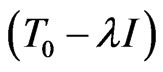 is invertible;
is invertible;
• And the map 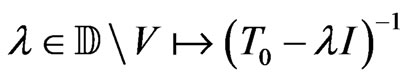 is continuous (see [6]).
is continuous (see [6]).
It follows that
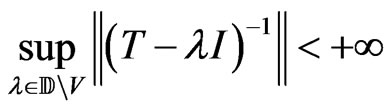
since  is compact. Put
is compact. Put
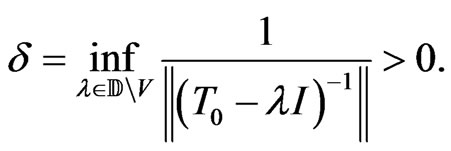
Let 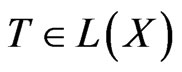 such that
such that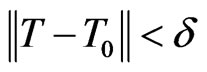 .
.
For any 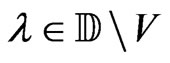 we have
we have
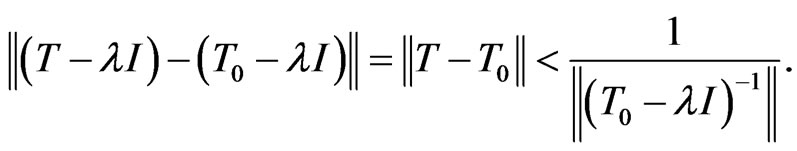
Thus, 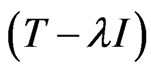 is invertible and hence
is invertible and hence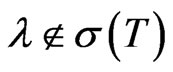 . In other terms,
. In other terms, 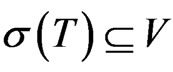 for all
for all 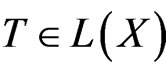 with
with 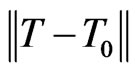
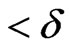 . Therefore
. Therefore 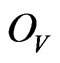 is an open subset of
is an open subset of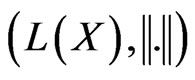 .
.
3. Strong Operator Topology and the Spectrum Function
Consider now 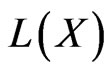 equipped with the strong operator topology
equipped with the strong operator topology 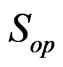 (see [6]). In general,
(see [6]). In general, 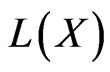 equipped with the strong operator topology is not a polish space (since it is not a Baire space). However, if
equipped with the strong operator topology is not a polish space (since it is not a Baire space). However, if 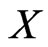 is separable, then
is separable, then 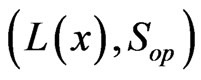 is a standard Borel space. Indeed, it is Borel-isomorph to a Borel subset of the Polish space
is a standard Borel space. Indeed, it is Borel-isomorph to a Borel subset of the Polish space 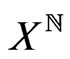 equipped with the norm product topology via the map
equipped with the norm product topology via the map
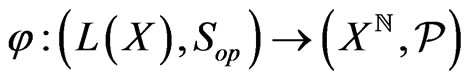
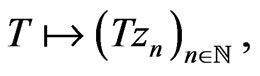
where 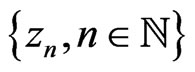 is a dense
is a dense 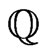 -vector space in
-vector space in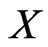 .
.
The next result shows how this topology on 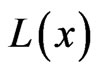 affects the spectrum function.
affects the spectrum function.
Theorem 1 For any separable infinite dimensional Banach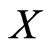 , the map
, the map
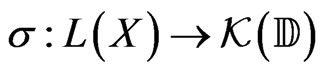
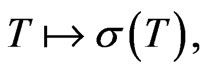
which maps a bounded operator to its unit spectrum, is Borel when 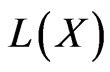 is endowed with the strong operator topology
is endowed with the strong operator topology 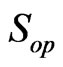 and
and 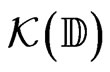 with the Hausddorf topology.
with the Hausddorf topology.
Proof 3 As 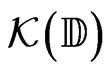 is equipped with the Hausdorff topology, it follows from the proposition 1, that it is enough to show that for any open subset
is equipped with the Hausdorff topology, it follows from the proposition 1, that it is enough to show that for any open subset 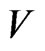 of the disc
of the disc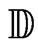 , the following subset
, the following subset 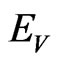 is Borel in
is Borel in 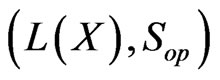
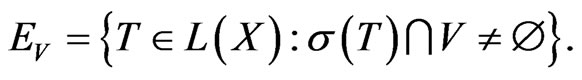
Let 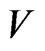 be a fixed open subset of
be a fixed open subset of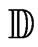 . We have
. We have
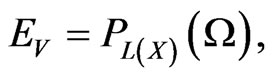
where 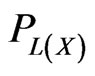 stands for the canonical projection of
stands for the canonical projection of 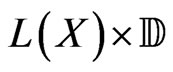 onto
onto , and
, and
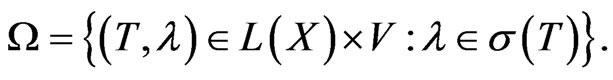
By a descriptive set theory result from ([7]), to show that 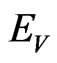 is a Borel set it suffices to show that
is a Borel set it suffices to show that  is a Borel set with
is a Borel set with 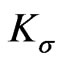 vertical sections.
vertical sections.
For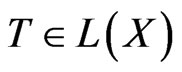 , the vertical section of the set
, the vertical section of the set 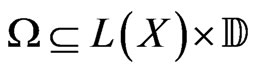 along the direction
along the direction 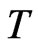 is given by
is given by

Thus, it is indeed a 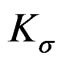 of
of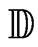 .
.
Now, we need to prove that  is a Borel set. Put
is a Borel set. Put
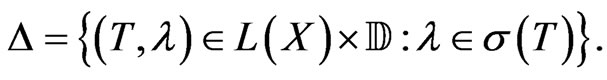
Therefore
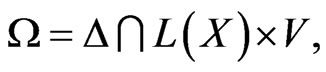
Hence, to finish the proof, it is enough to prove the following claim.
Claim: 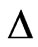 is a Borel set of
is a Borel set of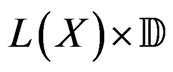 .
.
First, note that 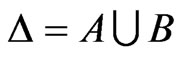 with
with
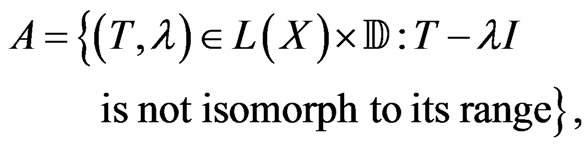
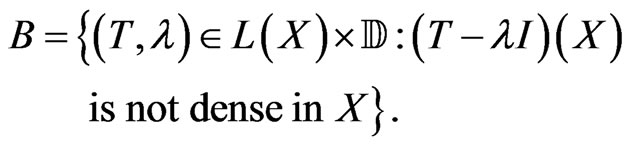
Indeed, if 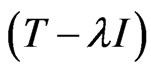 is an isomorphism onto its range, then
is an isomorphism onto its range, then 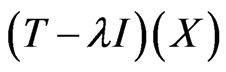 is a closed subspace that will be strict if
is a closed subspace that will be strict if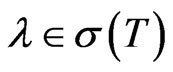 , and thus not dense in
, and thus not dense in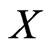 . On the other hand, since
. On the other hand, since 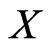 is separable, there exists a countable and dense subset
is separable, there exists a countable and dense subset 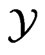 in the sphere
in the sphere 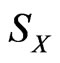 of
of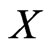 , and there exists a dense sequence
, and there exists a dense sequence 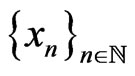 in
in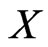 .
.
Now, we will show that 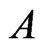 and
and 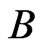 are Borel sets. Let
are Borel sets. Let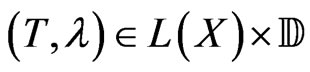 . From the definition of
. From the definition of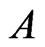 , We have
, We have 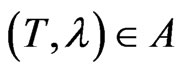 if and only if
if and only if
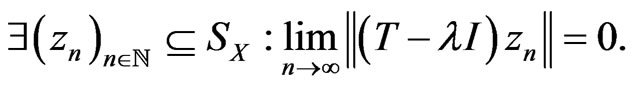
In other terms, this is equivalent to
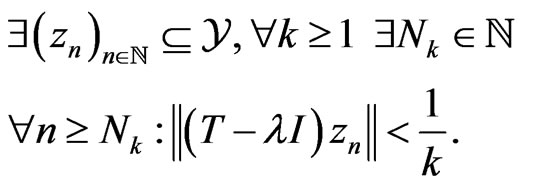
By choosing the subsequence 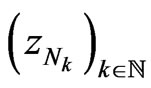 instead of
instead of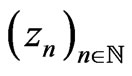 , the previous statement is equivalent to
, the previous statement is equivalent to
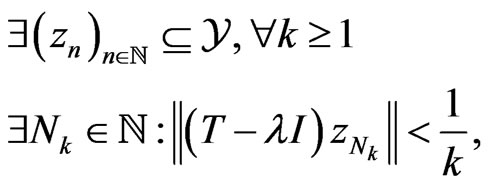
or again,
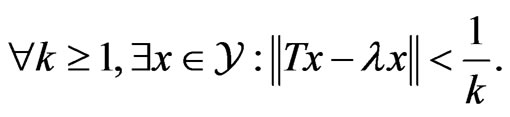
Therefore,
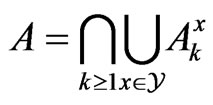
with
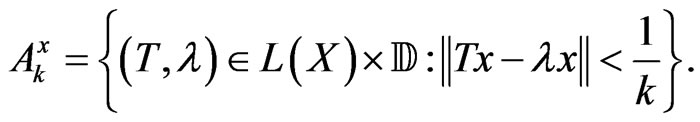
Since 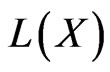 is equipped with the the strong operator convergence
is equipped with the the strong operator convergence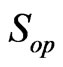 , it follows that the sets
, it follows that the sets 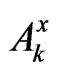 are open. Hence,
are open. Hence, 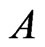 is a Borel set.
is a Borel set.
On the other hand, “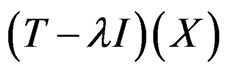 is not dense in
is not dense in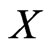 ” is equivalent to
” is equivalent to
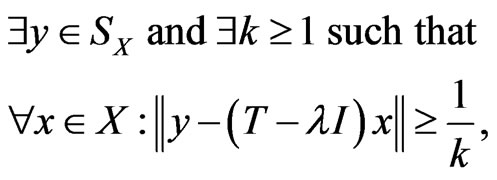
or again,
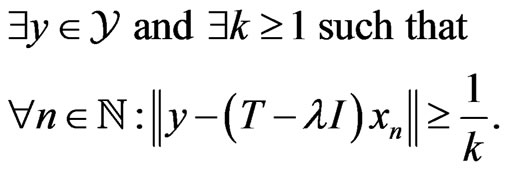
Therefore

with
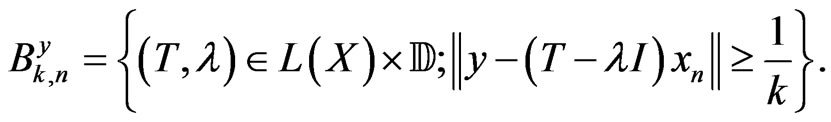
Similarly to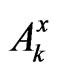 , it is not difficult to see that the sets
, it is not difficult to see that the sets 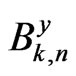 are Borel sets. Hence
are Borel sets. Hence 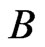 is also a Borel set. This proves the claim and ends the proof of the theorem 1.
is also a Borel set. This proves the claim and ends the proof of the theorem 1.
4. Conclusions
The variation of the unit spectrum of operators in infinite dimensional Banach spaces is investigated. The unit spectrum of an operator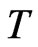 , denoted by
, denoted by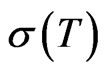 , is defined as the restriction on the closed unit disc
, is defined as the restriction on the closed unit disc 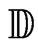 of the complex plane
of the complex plane 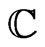 of the spectrum of
of the spectrum of 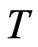 given by
given by .
.
First, the paper presents a simplified characterization of the Borel structure making the set 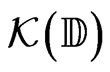 of compact subsets of the closed unit disc
of compact subsets of the closed unit disc 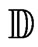 a Polish space. It is also shown that for a Banach space
a Polish space. It is also shown that for a Banach space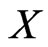 , the map
, the map 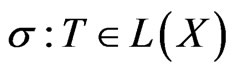 that for an operator associates its unit spectrum
that for an operator associates its unit spectrum 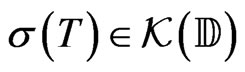 is upper-semi continuous when
is upper-semi continuous when 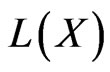 is endowed with the norm of operators. On the other hand, when
is endowed with the norm of operators. On the other hand, when 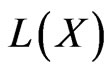 is endowed with the strong operator topology, it is shown that first
is endowed with the strong operator topology, it is shown that first 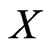 needed to be a separable infinite dimensional Banach to guarantee a standard Borel structure on
needed to be a separable infinite dimensional Banach to guarantee a standard Borel structure on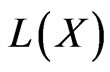 , then it is shown that the that the map
, then it is shown that the that the map 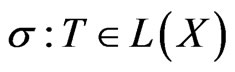 is Borel in this case. Therefore, this topology is making the spectrum function more rigourous, and as a consequence the variations of the spectrum following changes in an operator or a sequence of operators.
is Borel in this case. Therefore, this topology is making the spectrum function more rigourous, and as a consequence the variations of the spectrum following changes in an operator or a sequence of operators.
REFERENCES
- M. Damak and A. Jeribi, “On the Essential Spectra of Matrix Operators and Applications,” Electronic Journal of Differential Equations, Vol. 2007, No. 11, 2007, pp. 1-16.
- A. Jeribia, N. Moalla and I. Walhaa, “Spectra of Some Block Operator Matrices and Application to Transport Operators,” Doklady Akademii Nauk SSSR (N.S.), Vol. 351, No. 1, 2009, pp. 315-325.
- A.S. Kechris and A. Louveau, “Descriptive Set Theory and the Structure of Sets of Uniqueness,” Cambridge University Press, Cambridge, 1987.
- K. Kuratowski, “Topology,” Vol. II, Academic Press New York, 1966.
- J. P. R. Christensen, “Topology and Borel Structure,” North-Holland Mathematics Studies, Vol. 10, Elsevier, Amsterdam, 1974.
- N. Dunford and J. Schwartz, “Linear Operator,” Part. I, DA Wiley-Interscience Publication, New York, London, Sydney, 1971.
- J. Saint Raymond, “Boréliens à Coupes
 ,” Bulletin de la Société Mathématique de France, Vol. 104, 1976, pp. 389-400.
,” Bulletin de la Société Mathématique de France, Vol. 104, 1976, pp. 389-400.

