Advances in Pure Mathematics
Vol.3 No.6(2013), Article ID:36380,7 pages DOI:10.4236/apm.2013.36074
A Construction That Produces Wallis-Type Formulas
School of Mathematical Sciences, Rochester Institute of Technology, Rochester, USA
Email: JMF7126@rit.edu, DLFSMA@rit.edu
Copyright © 2013 Joshua M. Fitzhugh, David L. Farnsworth. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received June 18, 2013; revised July 23, 2013, accepted August 21, 2013
Keywords: Wallis’s Formula; Unit p-Circle; Infinite Product; p; Gamma Function
ABSTRACT
Generalizations of the geometric construction that repeatedly attaches rectangles to a square, originally given by Myerson, are presented. The initial square is replaced with a rectangle, and also the dimensionality of the construction is increased. By selecting values for the various parameters, such as the lengths of the sides of the original rectangle or rectangular box in dimensions more than two and their relationships to the size of the attached rectangles or rectangular boxes, some interesting formulas are found. Examples are Wallis-type infinite-product formulas for the areas of p-circles with p > 1.
1. Introduction
Wallis’s product formula for p/2 is
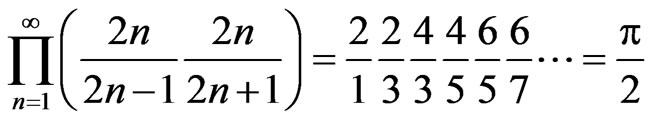 . (1)
. (1)
Two more-or-less elementary proofs are given in [1,2]. An interesting geometric construction, which first appeared in [3], produces this infinite product. The construction is somewhat generalized in [4,5].
The purpose of this paper is to further generalize the construction in [3]. Among the naturally occurring special cases of the generalization are infinite-product representations of areas of p-circles. In Section 2, we give an account of the construction and some generalizations. In Section 3, we review the gamma function, since our results are written in terms of that function. Section 4 describes unit super-circles or p-circles  for p ≥ 1, since their areas are produced by certain generalizations of the construction. Section 5 contains several interesting outcomes of some new generalizations of the geometric construction, including the Wallis formula for p-circles.
for p ≥ 1, since their areas are produced by certain generalizations of the construction. Section 5 contains several interesting outcomes of some new generalizations of the geometric construction, including the Wallis formula for p-circles.
2. The Construction
The following construction produces the Wallis product (1) [3-5]. See Figure 1. Let wj be the width and hi be the height of the current rectangle at the current step for the appropriate values of i and j.
The initial square and the first few steps in the construction are:
• The initial square in Figure 1(a) has sides w0 = 1 and h0 = 1 and area 1.
• The first step is to attach to the right a square with sides w1 ‒ w0 = 1 and h0 = 1, so that the current rectangle in Figure 1(b) has sides w1 = 2 and h0 = 1 and area 2.
• The second step is to attach to the top a rectangle of area 1 with sides w1 = 2 and h1 – h0 = 1/2, so that the current rectangle in Figure 1(c) has sides w1 = 2 and h1 = 3/2 and area 3.
• The third step is to attach to the right a rectangle of area 1 with sides w2 – w1 = 2/3 and h1 = 3/2, so that the current rectangle in Figure 1(d) has sides w2 = 8/3 and h1 = 3/2 and area 4.
• The fourth step is to attach to the top a rectangle of area 1 with sides w2 = 8/3 and h2 – h1 = 3/8, so that the current rectangle in Figure 1(e) has sides w2 = 8/3 and h2 = 15/8 and area 5.
The construction continues indefinitely in this way.
In [3-5], it is shown that
 , (2)
, (2)
which is p/2 by Wallis’s product formula (1).
Short [4] and Short and Melville [5] generalize the construction with all the rectangles adjoined to the right having area A, all the rectangles adjoined to the top having
 (a)
(a)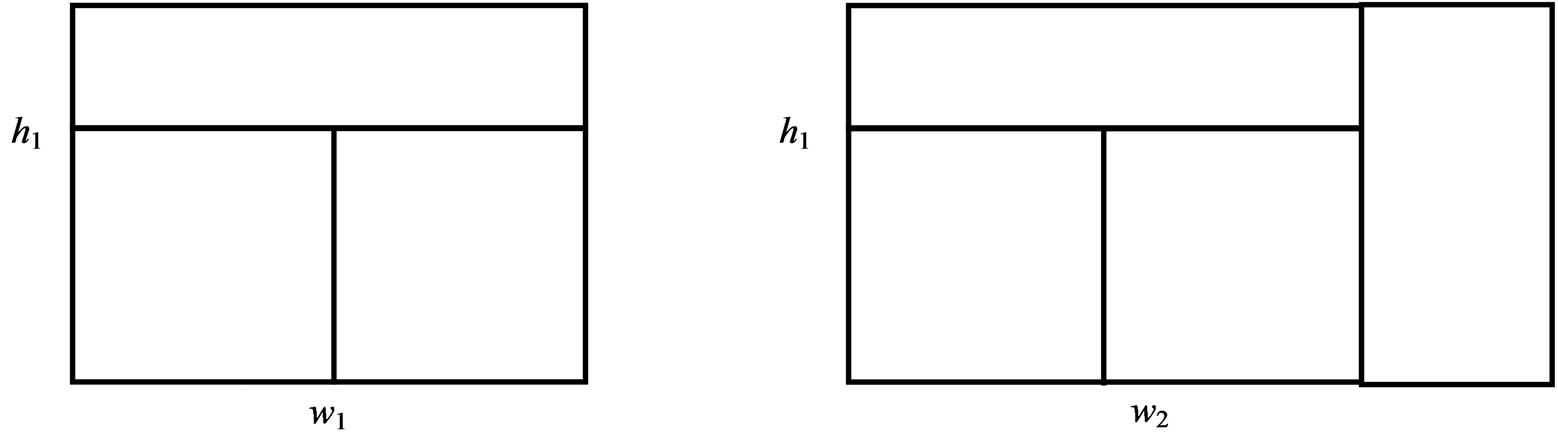 (b)
(b)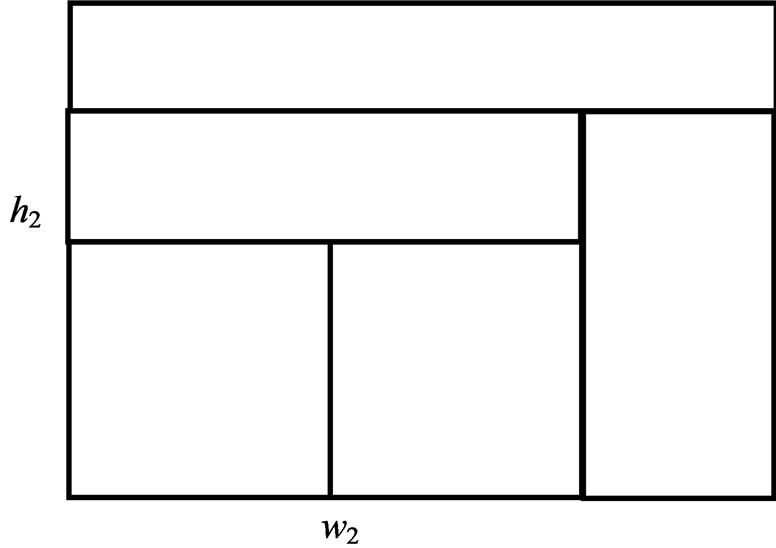 (c)
(c)
Figure 1. The initial unit square and the first four steps of the construction.
area B, and the initial square having area . They show that:
. They show that:
If A > B, then ; if A < B, then
; if A < B, then ; and if A = B, then
; and if A = B, then 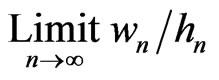 converges.
converges.
For the last case, they demonstrate how averaging methods can be employed to obtain  numerically to a desired precision.
numerically to a desired precision.
These results are examples in the further generalizations in Section 5, so we do not discuss their details. The generalizations in Section 5 include allowing the initial figure to be a rectangle and increasing the dimensionality of the construction. Properties of the gamma function are very useful and are reviewed in the next section.
3. The Gamma Function
The purpose of this section is to remind readers about some properties of the gamma function, including infinite-product representations. A source that is relatively complete and takes a historical perspective is [6]. We restrict the domain of the gamma function to the positive real numbers, since only those values concern us. The most familiar definition of the gamma function is the convergent, improper integral
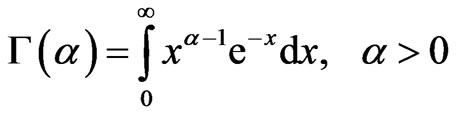 , (3)
, (3)
which is known as Euler’s Integral of the Second Kind [7, p. 241].
Integrating (3) by parts gives
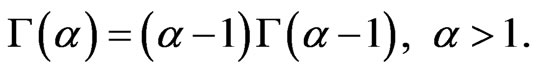 (4)
(4)
For positive integer a,

Two special values are
 , (5)
, (5)
and
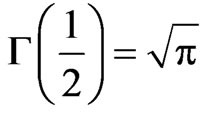 (6)
(6)
[7, p. 240,8, p. 459,9, p. 508].
A formulation as a limit is
 (7)
(7)
which can be derived from (3) [7, pp. 242-243,8, pp. 458-459,9, pp. 506-507]. Often, Tannery’s theorem is cited in proofs. An infinite product representation is
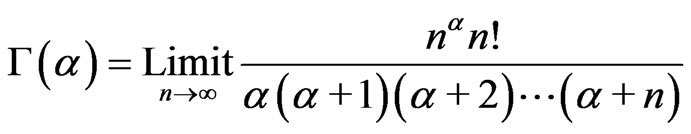 which can be derived by the change of variable x = ny in (7) and performing n integrations by parts [7, pp. 241- 243,9, p. 506].
which can be derived by the change of variable x = ny in (7) and performing n integrations by parts [7, pp. 241- 243,9, p. 506].
The identity
 (8)
(8)
which is valid for
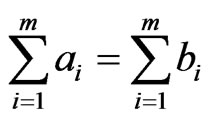 (9)
(9)
[7, pp. 238-239, 9, p. 115], greatly simplifies many derivations in Section 5. The infinite product on the left-hand side of (8) would have diverged if there were not the same number of terms in its numerator and denominator or if (9) were not satisfied. Taking a1 = a2 = 0 and b1 = ‒b2 = ‒1/2, we obtain the Wallis product formula (1), since

Euler’s Integral of the First Kind, also known as the beta function, is
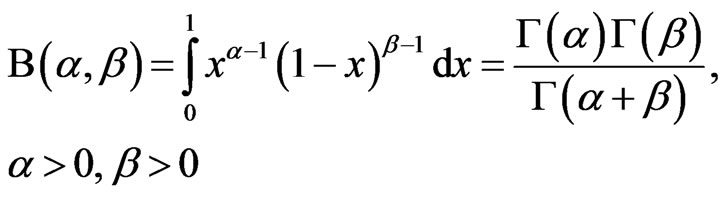 (10)
(10)
[7, pp. 253-256].
4. Super Circles
In the same way that Euclidean geometry is based on the unit circle x2 + y2 = 1, lp geometries, p ≥ 1, are based on the unit super-circle or p-circle . These are Minkowski geometries, which are characterized by their unit circles that enclose a convex, symmetric region [10]. See Figure 2 for graphs of the lp unit circles for p = 1, 3/2, 2, and 4.
. These are Minkowski geometries, which are characterized by their unit circles that enclose a convex, symmetric region [10]. See Figure 2 for graphs of the lp unit circles for p = 1, 3/2, 2, and 4.

Figure 2. The lp unit circles |x|p + |y|p = 1 for p = 1, 3/2, 2, and 4.
The enclosed area of the lp super circle is
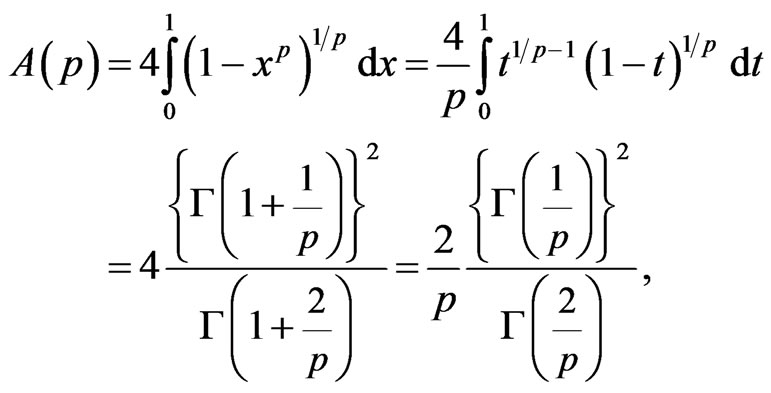 (11)
(11)
using (4) and (10), where t = xp. The enclosed region is not convex for 0 < p < 1, so the circle does not give a Minkowski geometry; however, (11) gives the areas of those regions. For p = 2, (11) gives p, using (4), (5), and (6). The enclosed area of the upper half of the lp super circle is
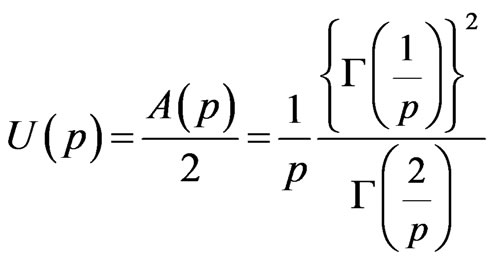 . (12)
. (12)
5. Generalizations of the Construction
The generalizations in this section include allowing the initial figure to be a rectangle and increasing the dimensionality of the construction. Selecting various values for the parameters gives interesting formulas, including Wallis-type formulas for half the areas of p-circles.
5.1. Starting with a Rectangle in Two Dimensions
The first generalization of the construction is to begin with a rectangle with width a and height b, instead of a square, so that
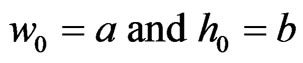 . (13)
. (13)
The adjoined rectangles have areas A and B, as described in Section 2.
The iterative steps of adjoining rectangles are determined by
 (14)
(14)
and
 , (15)
, (15)
for n ≥ 0, giving the next values of wn+1 and hn+1 in turn. After 2n steps, the area of the whole figure, which is a rectangle, is
 , (16)
, (16)
and after 2n + 1 steps, the area of the rectangle is
 . (17)
. (17)
We find recursion relationships between wn+1 and wn and between hn+1 and hn. Substituting (16) into (14) gives
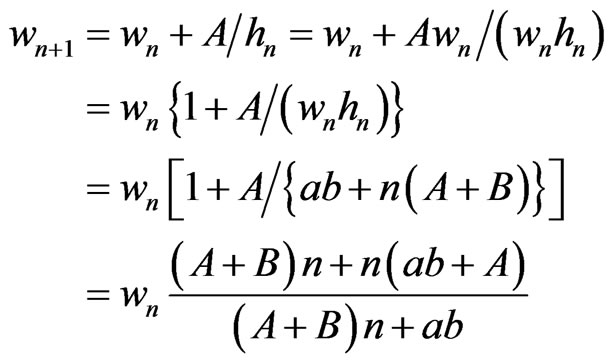 (18)
(18)
for n ≥ 0. Substituting (17) into (15) gives
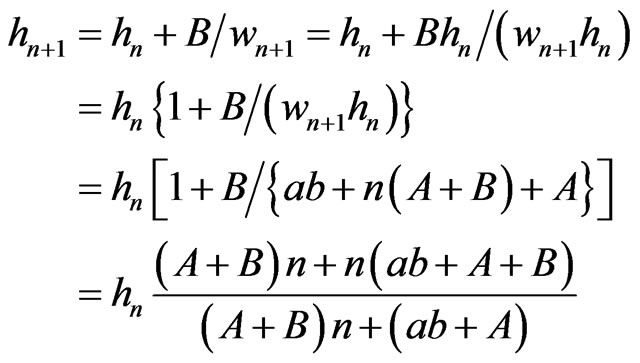 (19)
(19)
for n ≥ 0.
Dividing (18) by (19) gives
 (20)
(20)
From (13) and (20)
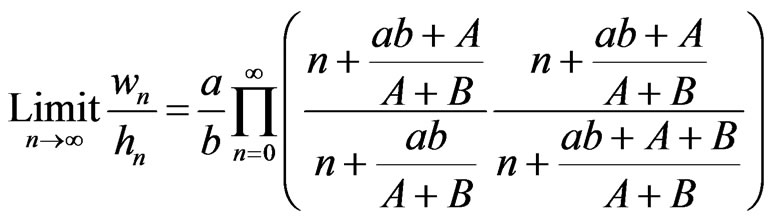 .
.
In order to apply (8), the index in the infinite product must start at 1, not 0. Changing the index to m = n + 1 and reverting back to n give
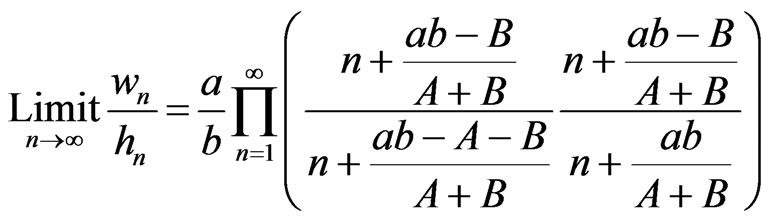 . (21)
. (21)
Then,
 if and only if
if and only if
 (22)
(22)
from (8) and (9). Equation (22) implies that A = B for any values of a and b and, using (4),
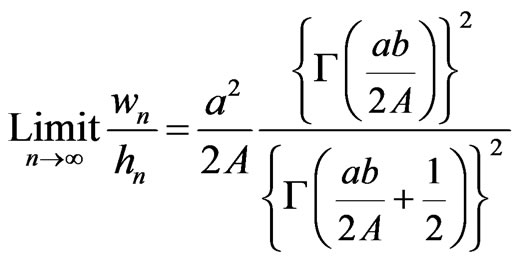 . (23)
. (23)
For the special case a = b = A = B = 1, (21) and (23) is the Wallis product (1) with (2). Also, this is U(2) from (12).
5.2. Three Dimensions
There is a large variety of ratios and limits to investigate when the dimensionality is increased. In three dimensions, the process is determined by the initial box with sides
 (24)
(24)
and adjoining rectangular boxes, instead of rectangles. The iterative steps of adjoining rectangular boxes of volumes A, B, and C are determined by
 , (25)
, (25)
 , (26)
, (26)
and
 . (27)
. (27)
After 3n steps, the volume of the whole rectangular box is
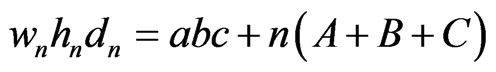 , (28)
, (28)
after 3n + 1 steps, the volume is
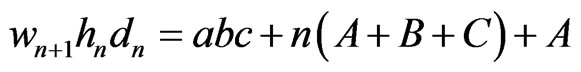 , (29)
, (29)
and after 3n + 2 steps, the volume is
 . (30)
. (30)
Solving (25) for  and using (28) gives
and using (28) gives
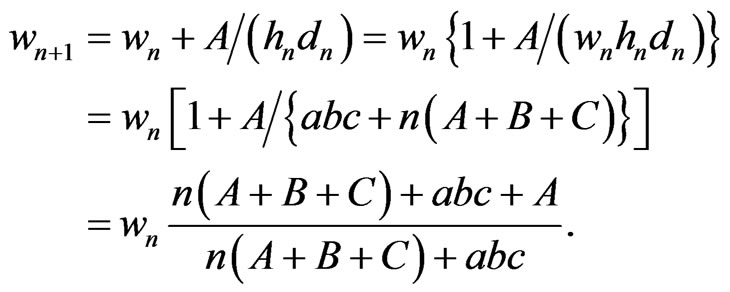 (31)
(31)
Similarly, (26) and (29) give
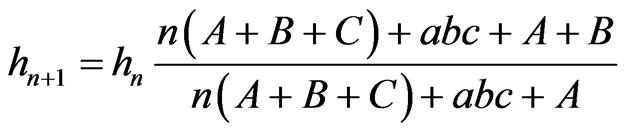 , (32)
, (32)
and (27) and (30) give
 . (33)
. (33)
Limits of ratios of (31), (32), and (33) give a variety of interesting expressions. We present three examples for wn/dn. Dividing (31) by (33) gives
 (34)
(34)
From (24) and (34)
 .
.
Changing the index to m = n + 1 and reverting back to n give
 (35)
(35)
Then,

if and only if
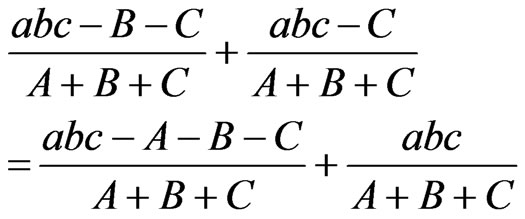 (36)
(36)
from (8) and (9). Equation (36) implies that A = C for any values of a, b, c, and B and, using (4),
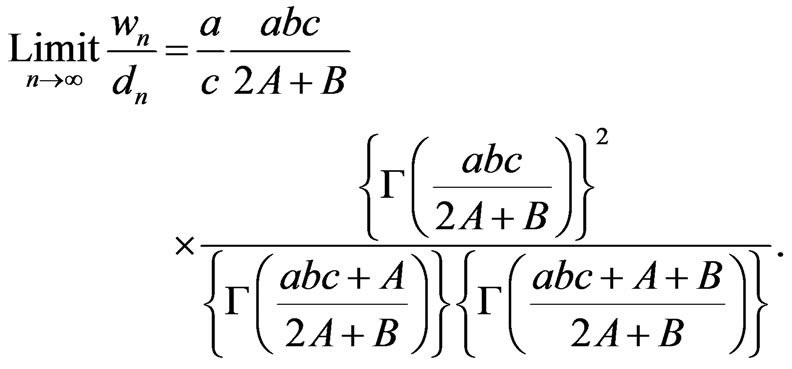 (37)
(37)
Consider three special cases of (37). For the first one, set a = b =c = A = B = C = 1, then (12), (35), and (37) give
 (38)
(38)
For the second special case, set , a = c, and A = abc in (35) and (37) to obtain
, a = c, and A = abc in (35) and (37) to obtain
 (39)
(39)
for p > 2. The domain of U(p) is restricted by
 .
.
For the third case, set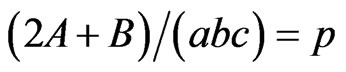 , a = c, and A + B = abc in (35) and (37) to obtain
, a = c, and A + B = abc in (35) and (37) to obtain
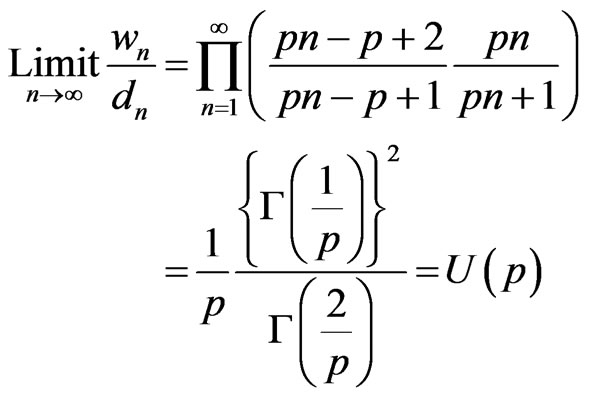 (40)
(40)
for 1 < p < 2. The domain is restricted by

Using this construction, Wallis-type product formulas have been obtained for half the areas of p-circles for p > 1.
5.3. N Dimensions
For the construction in N dimensions, we limit the initial shape to be a unit hypercube and each adjoined shape to be rectangular of unit hyper volume. The nth value of the ith side’s length is sn(i), and the initial sides’ lengths are s0(i) = 1 with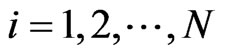 .
.
Analogous to (14) and (15) in Subsection 5.1 for two dimensions and (25), (26), and (27) in Subsection 5.2 for three dimensions, the iterative steps of adjoining rectangular boxes are determined by
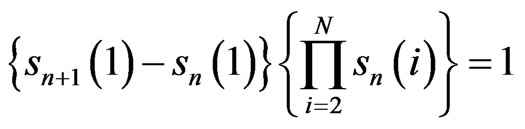
for the (Nn + 1)th step,
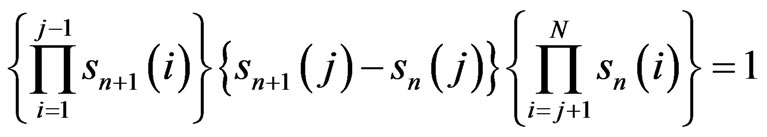
for the (Nn + j)th step with 1 < j < N, and

for the (Nn + N)th step. Analogous to (16) and (17) in Subsection 5.1 for two dimensions and (28), (29), and (30) in Subsection 5.2 for three dimensions, the volumes are

after the (Nn)th step, and
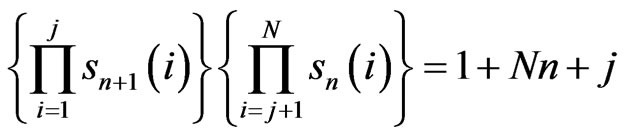
after the (Nn + j)th step with 1 ≤ j ≤ N – 1.
Using an analysis paralleling Subsections 5.1 and 5.2, we obtain
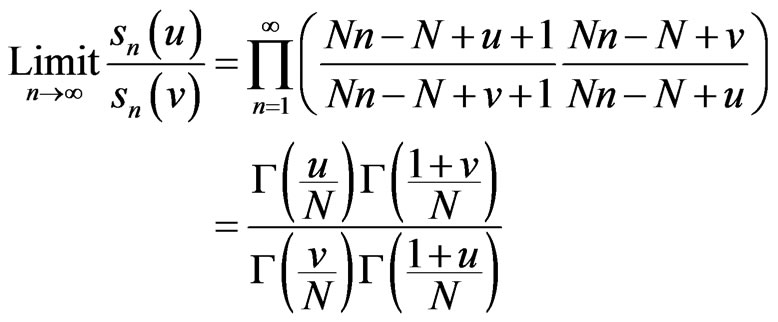
for all u and v equal to . For u = 1 and v = N,
. For u = 1 and v = N,
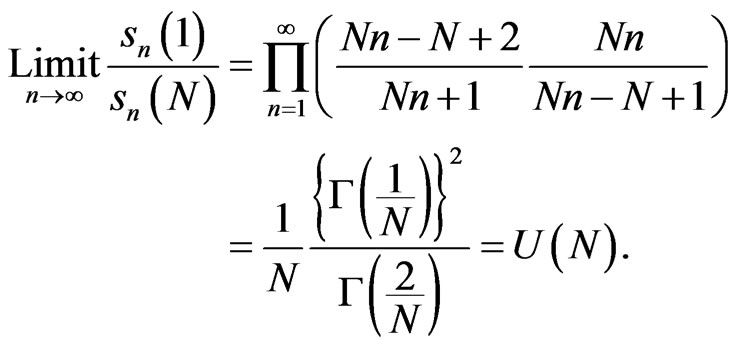 (41)
(41)
For N = 2, (41) is the Wallis formula (1) with (2), and for N = 3, it is (38).
6. Summary
We have generalized the infinite geometric construction of attaching rectangles to a square, which was originally presented in [3], by allowing the initial square to be replaced with a rectangle and by increasing the dimensionality of the construction. Selecting values for the various parameters, such as the lengths of the sides of the original rectangle or rectangular box in dimensions more than two and their relationships to the size of the attached rectangles or rectangular boxes, gives some interesting formulas. Examples are Wallis-type formulas (38) through (41) for half the areas of p-circles with p > 1.
REFERENCES
- S. J. Miller, “A Probabilistic Proof of Wallis’s Formula for p,” The American Mathematical Monthly, Vol. 115, No. 8, 2008, pp. 740-745.
- J. Wästlund, “An Elementary Proof of the Wallis Product Formula for Pi,” The American Mathematical Monthly, Vol. 114, No. 10, 2007, pp. 914-917.
- G. Myerson, “The Limiting Shape of a Sequence of Rectangles,” The American Mathematical Monthly, Vol. 99, No. 3, 1992, pp. 279-280. doi:10.2307/2325077
- L. Short, “Some Generalizations of the Wallis Product,” International Journal of Mathematical Education in Science and Technology, Vol. 23, No. 5, 1992, pp. 695-707. doi:10.1080/0020739920230508
- L. Short and J. P. Melville, “An Unexpected Appearance of Pi,” Mathematical Spectrum, Vol. 25, No. 3, 1993, pp. 65-70.
- G. K. Srinivasan, “The Gamma Function: An Eclectic Tour,” The American Mathematical Monthly, Vol. 114, No. 4, 2007, pp. 297-315.
- E. T. Whittaker and G. N. Watson, “A Course in Modern Analysis,” 3rd Edition, Cambridge University Press, Cambridge, 1920.
- T. M. Apostol, “Mathematical Analysis,” Addison-Wesley, Reading, 1957.
- T. J. Bromwich, “An Introduction to the Theory of Infinite Series,” 2nd Edition Revised, Macmillan, London, 1926.
- A. C. Thompson, “Minkowski Geometry,” Cambridge University Press, Cambridge, 1996. doi:10.1017/CBO9781107325845

