Advances in Pure Mathematics
Vol.3 No.1A(2013), Article ID:27535,8 pages DOI:10.4236/apm.2013.31A023
Scattering of the Radial Focusing Mass-Supercritical and Energy-Subcritical Nonlinear Schrödinger Equation in 3D
1Department of Mathematics, Faculty of Education, Kassala University, Kassala, Sudan
2Department of Mathematics, Faculty of Pure and Applied Sciences, Fourah Bay College, University of Sierra Leone, Freetown, Sierra Leone
Email: mujahid@mail.ustc.edu.cn, amadu_fullah2005@yahoo.com
Received October 2, 2012; revised November 5, 2012; accepted November 13, 2012
Keywords: NLS; Blows-Up in Finite Time; Supremum; Precompactness
ABSTRACT
This paper studies the global behavior to 3D focusing nonlinear Schrödinger equation (NLS), the scaling index here is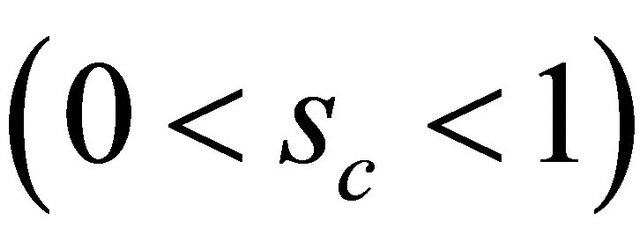 , which is the mass-supercritical and energy-subcritical, and we prove under some condition the solution
, which is the mass-supercritical and energy-subcritical, and we prove under some condition the solution 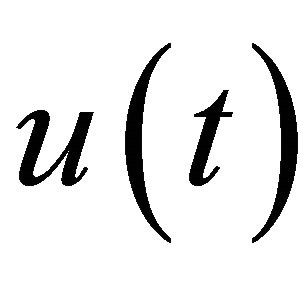 is globally well-posed and scattered. We also show that the solution “blows-up in finite time” if the solution is not globally defined, as
is globally well-posed and scattered. We also show that the solution “blows-up in finite time” if the solution is not globally defined, as  we can provide a depiction of the behavior of the solution, where T is the “blow-up time”.
we can provide a depiction of the behavior of the solution, where T is the “blow-up time”.
1. Introduction
Consider the Cauchy problem for the nonlinear Schrö- dinger equation (NLS) in dimensions d = 3:
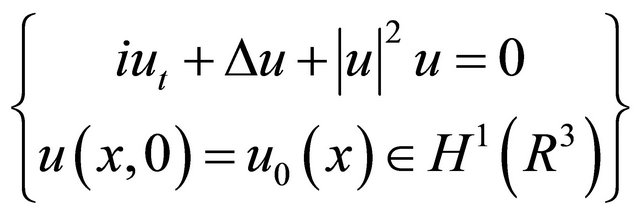 (1.1)
(1.1)
where 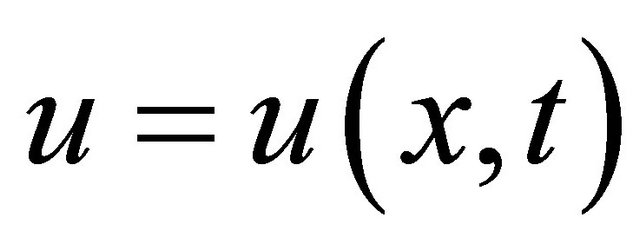 is a complex-valued function in
is a complex-valued function in 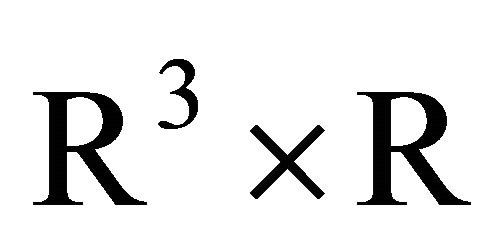 . The initial-value problem
. The initial-value problem 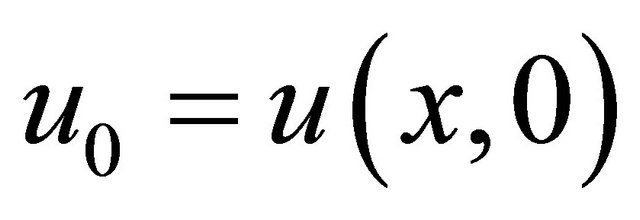 is locally well-posed in
is locally well-posed in .
.
In this paper we will study the focusing (NLS) problem, which is the mass-supercritical and energy-subcritical, where 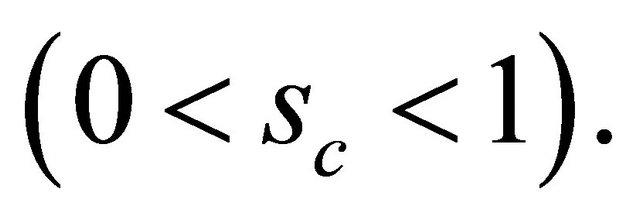
The Equation (1.1) has mass  where
where
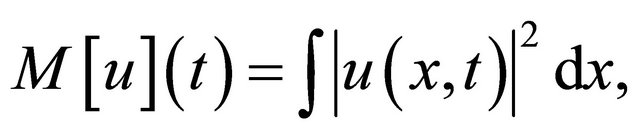
Energy  where
where
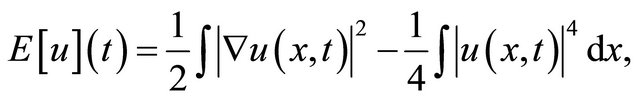
and Momentum 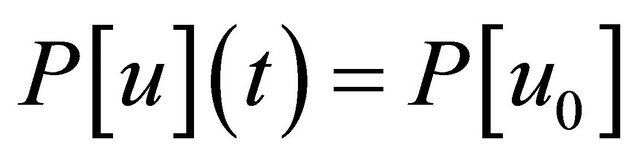 where
where
 .
.
If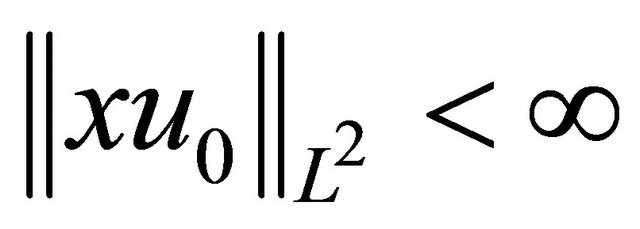 , then u satisfies
, then u satisfies
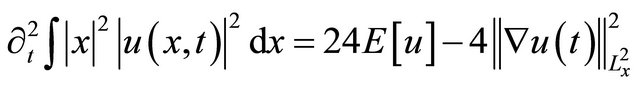 (1.2)
(1.2)
Equation (1.2) is said to be the Virial identity.
The Equation (1.1) has the scaling:
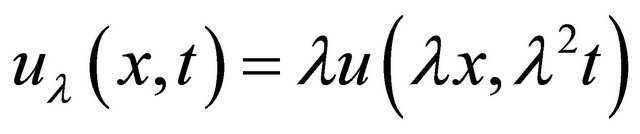
and also this scaling is a solution if  is a solution.
is a solution.
Moreover, u0 is a solution that is globally defined by u, if it is globally defined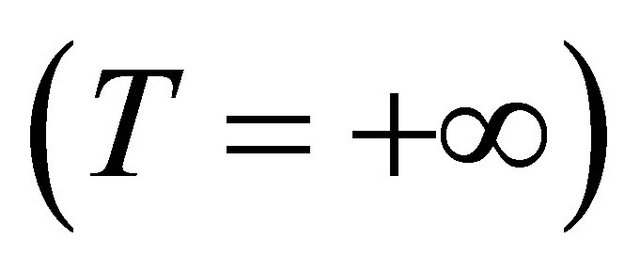 , and it does scatter (See [1,2]). We say the solution “blows-up in finite time”. If the solution is not globally defined, as
, and it does scatter (See [1,2]). We say the solution “blows-up in finite time”. If the solution is not globally defined, as , we can provide a depiction of the behavior of the solution, where T is the “blow-up time”. It follows from the H1 local theory optimized by scaling, that if blow-up in finite-time T > 0 happens, (see [3] or [4]), then there is a lower-bound on the “blow-up rate”:
, we can provide a depiction of the behavior of the solution, where T is the “blow-up time”. It follows from the H1 local theory optimized by scaling, that if blow-up in finite-time T > 0 happens, (see [3] or [4]), then there is a lower-bound on the “blow-up rate”:
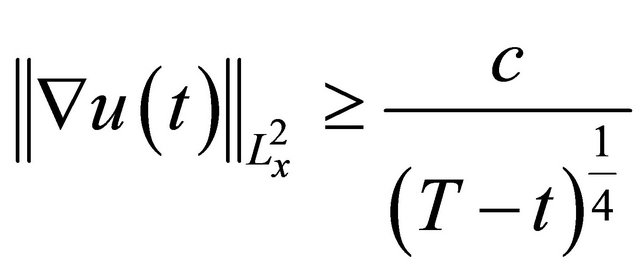 (1.3)
(1.3)
for some constant c. Thus, to prove global presence, it suffices to prove a global axiomatic bound on .
.
From the Strichartz estimates, there is a constant 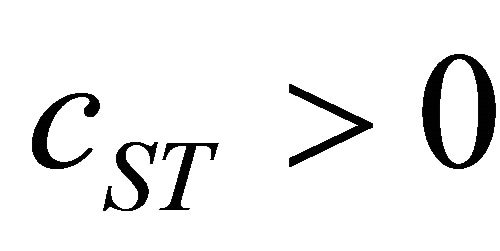 such that if
such that if 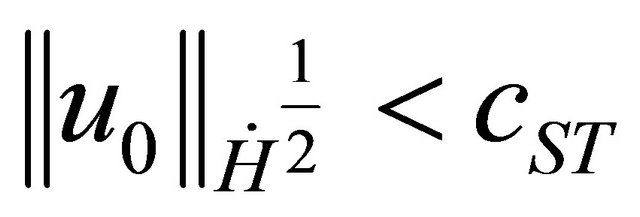 , then the solution
, then the solution 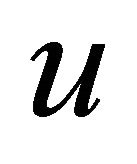 is globally defined and scattered.
is globally defined and scattered.
Note that the quantities 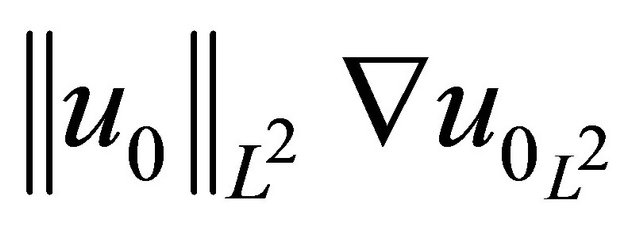 and
and
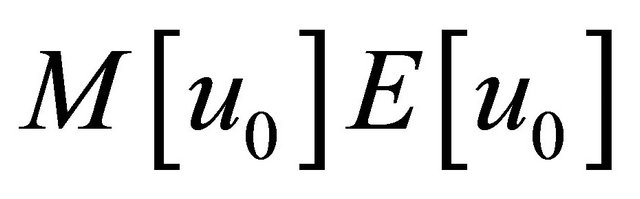 are also scale-invariant (See also [5]).
are also scale-invariant (See also [5]).
Let 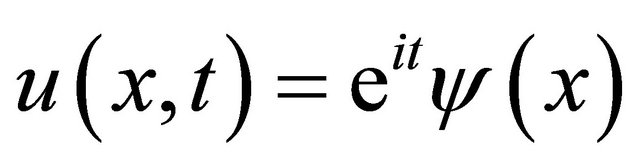 then u solves (1.1) as long as
then u solves (1.1) as long as
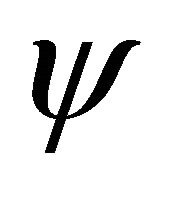 solves the nonlinear elliptic equation
solves the nonlinear elliptic equation
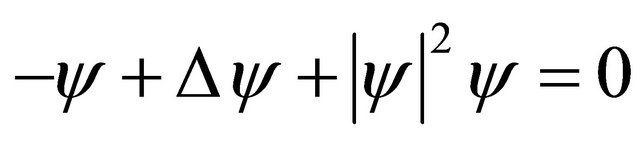 (1.4)
(1.4)
Equation (1.4) has an infinite number of solutions in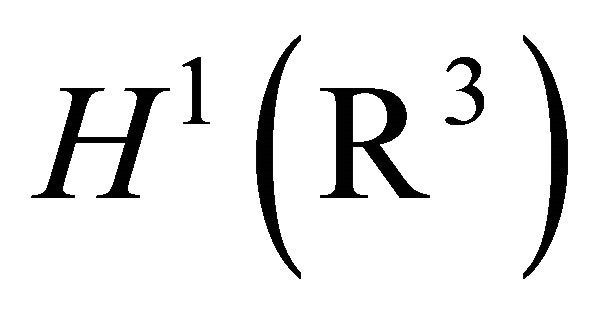 . The solution of minimal mass is denoted by
. The solution of minimal mass is denoted by 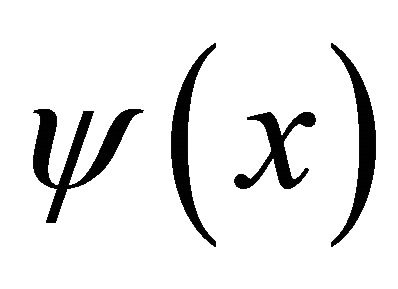 and for the properties of
and for the properties of  see [3,5,6].
see [3,5,6].
Under the condition , solutions to (1.1) globally exist if u0 satisfies;
, solutions to (1.1) globally exist if u0 satisfies;
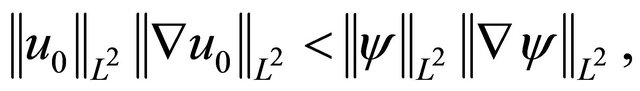 (1.5)
(1.5)
and there exist 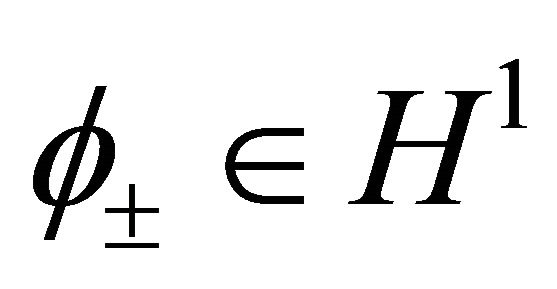 such that
such that
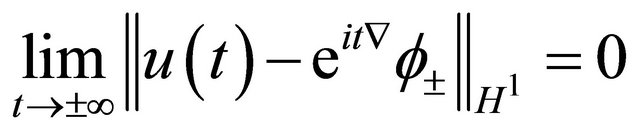 .
.
Theorem 1.1. Let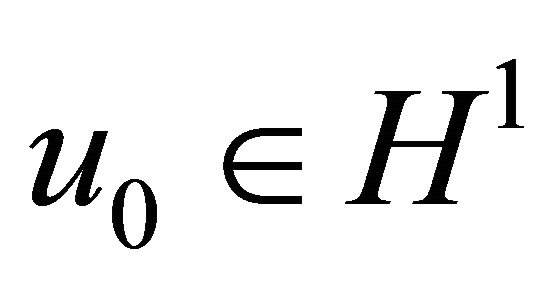 , and let
, and let 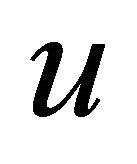 be the corresponding solution to (1.1) in H1. Suppose
be the corresponding solution to (1.1) in H1. Suppose
 (1.6)
(1.6)
If 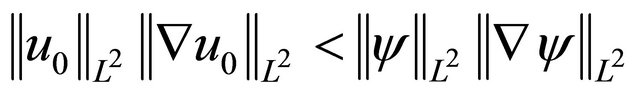 then u scatters in H1.
then u scatters in H1.
The argument of [6] in the radial case followed a strategy introduced by [7] for proving global well-posedness and scattering for the focusing energy-critical NLS. The beginning used a contradiction to the argument: suppose the sill for scattering is strictly below that claimed. This uniform localization enabled the use of a local Virial identity to be established, with the support of the sharp Gagliardo-Nirenberg inequality, an accurately positive lower bound on the convexity (in time) of the local mass of uc Mass conservation is then violated at enough large time.
We show in this paper, that the above program carries over to the non-radial setting with the extension of two key components.
Theorem 1.2. Suppose the radial H1 solution u to (1.1) blows-up at time 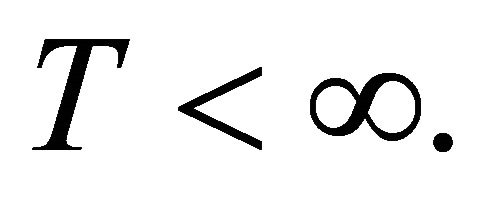 Then either there is a non-absolute
Then either there is a non-absolute  constant such that, as
constant such that, as 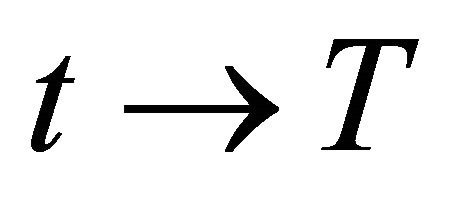
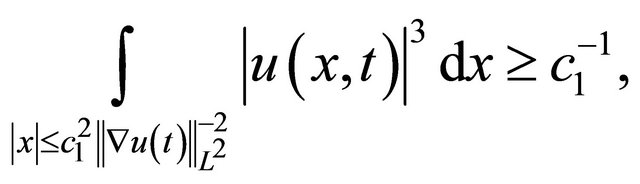 (1.7)
(1.7)
or there exists a sequence of times  such that for an absolute constant
such that for an absolute constant 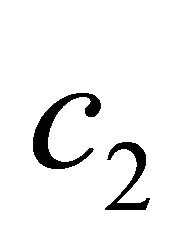
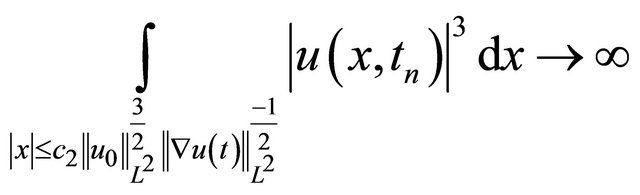 (1.8)
(1.8)
From (1.3), we have that the concentration in (1.7) satisfies , and the concentration in (1.8) satisfies
, and the concentration in (1.8) satisfies  (For more additional information see [8-10]).
(For more additional information see [8-10]).
Notation
Let 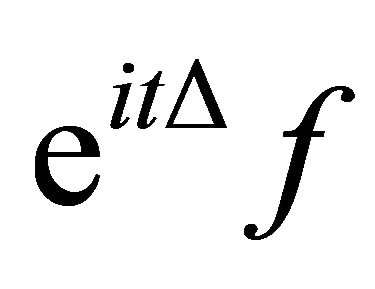 be the free Schrödinger propagator, and let
be the free Schrödinger propagator, and let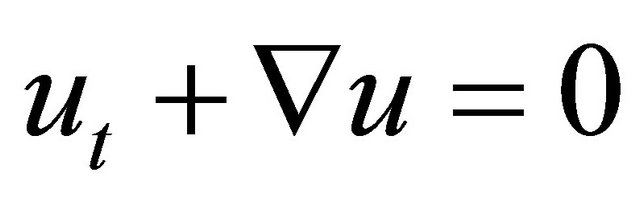 , with
, with 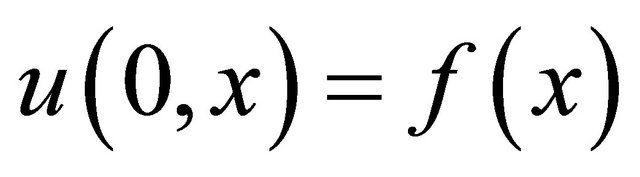 be linear equation, a solution in physical space, is given by:
be linear equation, a solution in physical space, is given by:
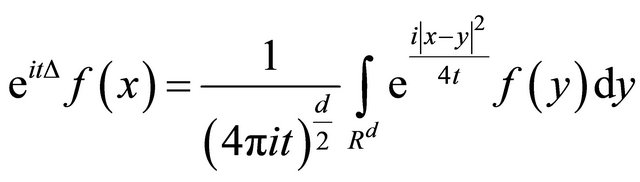 and in frequency space
and in frequency space
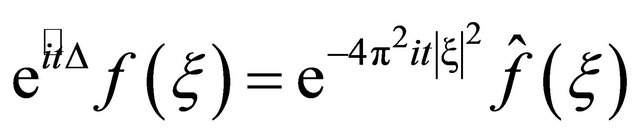
In particular, they save the Farewell homogeneous Sobolev norms and obey the dispersive inequality
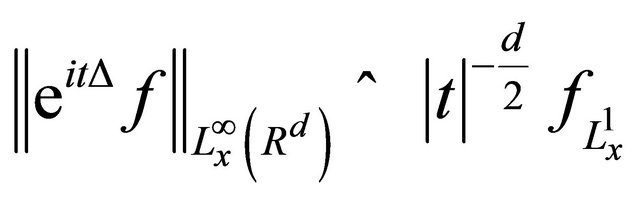 (1.9)
(1.9)
For all times .
.
Let 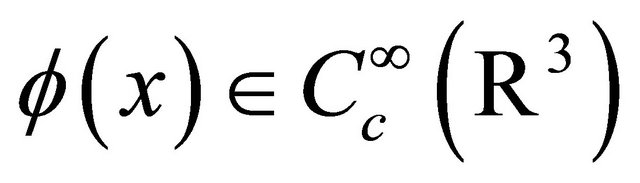 be a radial function, so that,
be a radial function, so that, 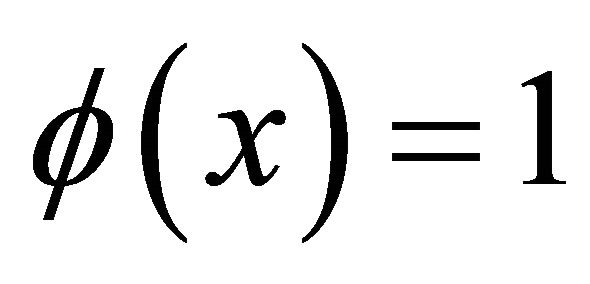 for
for  and
and 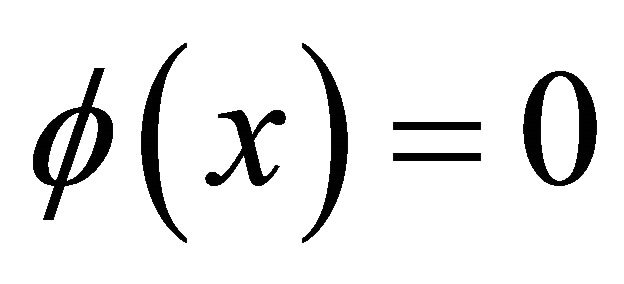 for
for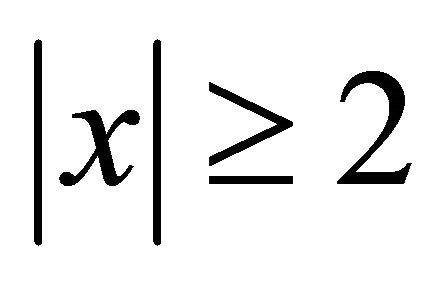 , Define the inner and outer spatial localizations of
, Define the inner and outer spatial localizations of  at radius
at radius 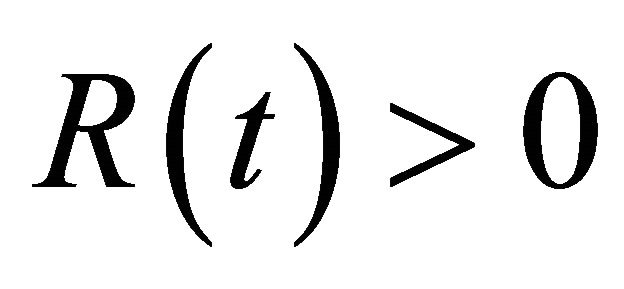 as
as
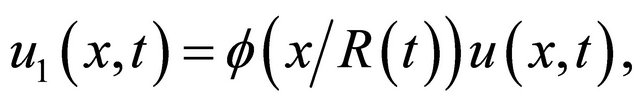
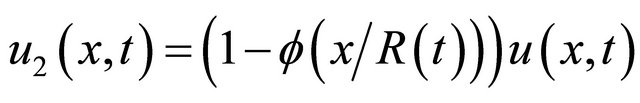
Let 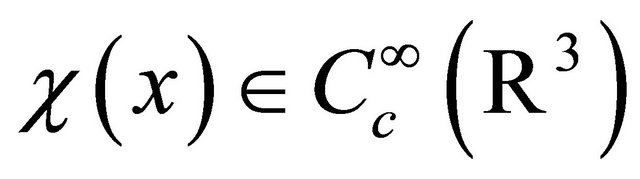 be a radial function so that,
be a radial function so that,
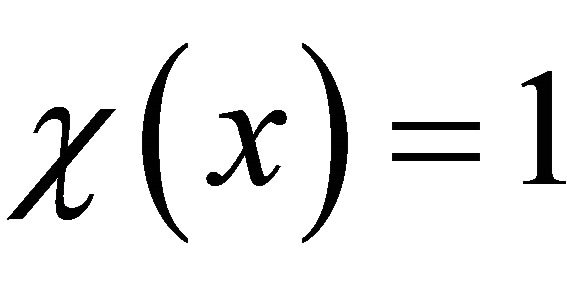 for
for 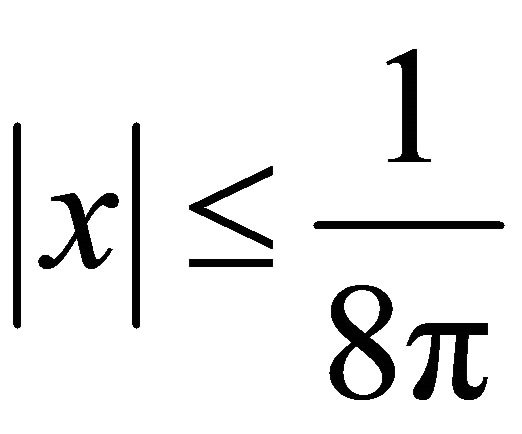 and
and 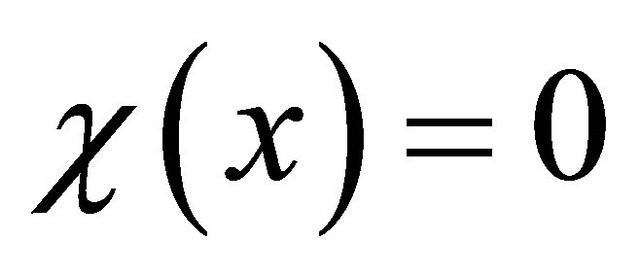 for
for 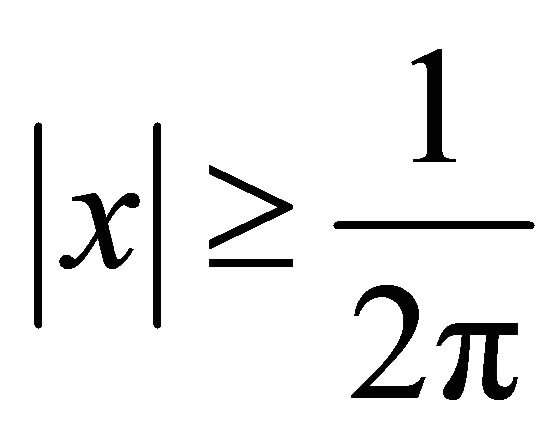 then
then
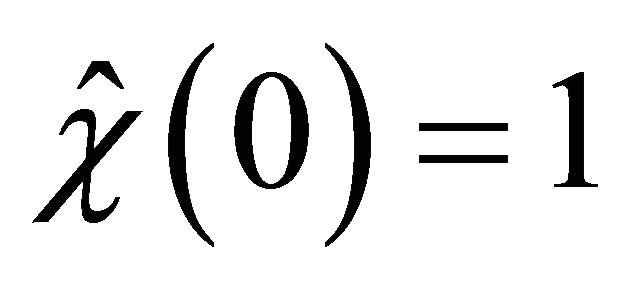 , and define the inner and outer indecision localizations at radius
, and define the inner and outer indecision localizations at radius 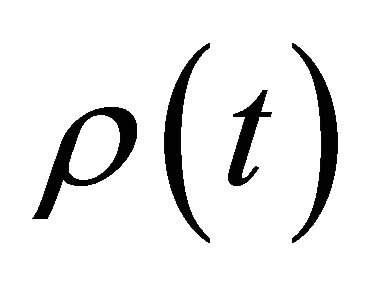 of u1 as
of u1 as
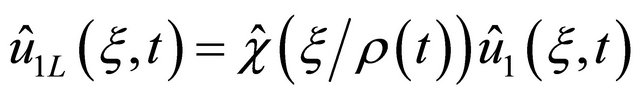 and
and
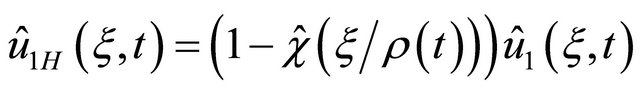 (the
(the  and
and  radii are chosen to be consistent with the assumption
radii are chosen to be consistent with the assumption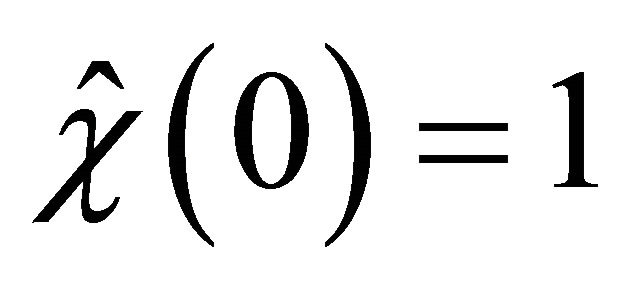 , since
, since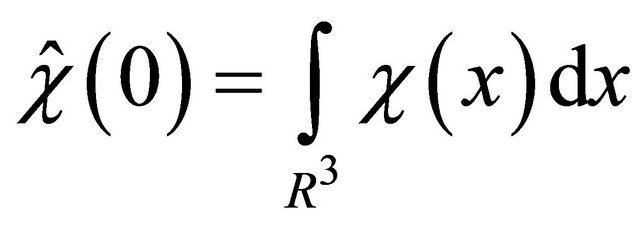 . In reality, this is for suitability only; the argument is easily proper to the case where
. In reality, this is for suitability only; the argument is easily proper to the case where 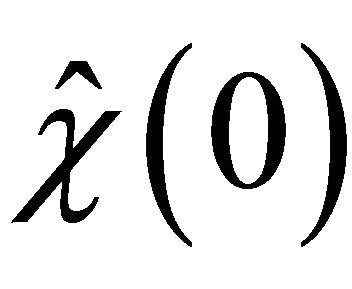 is any number
is any number ). We note that the indecision localization of
). We note that the indecision localization of  is inaccurate, though decisively we have;
is inaccurate, though decisively we have;
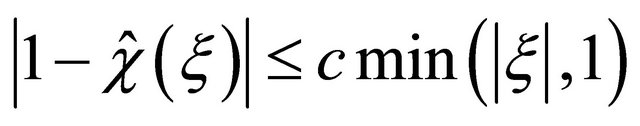 (1.10)
(1.10)
2. Proof of Theorem 1.2
In this section we discuss a proof of Theorem (1.2).
Proposition 2.1. Let u be an H1 radial solution to (1.1) that blows-up in finite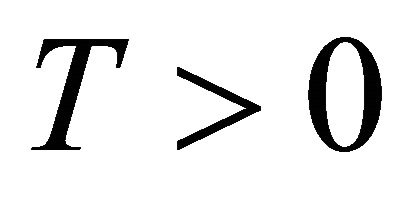 . Let
. Let
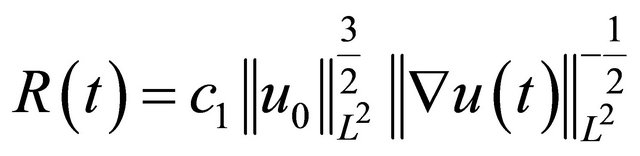
and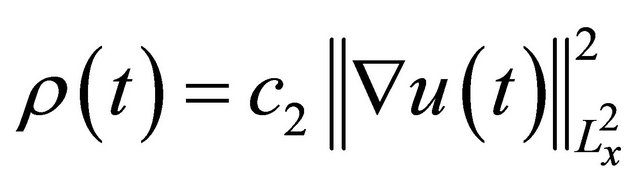 , (Where c1 and c2 are absolute constants), and
, (Where c1 and c2 are absolute constants), and 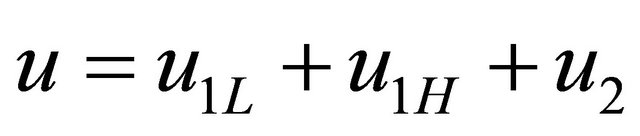 as characterized in the paragraph above.
as characterized in the paragraph above.
1) There exists an absolute constant 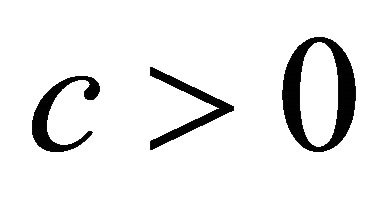 such that
such that
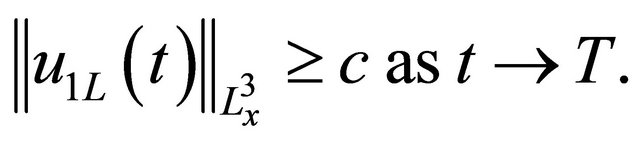 (2.1)
(2.1)
2) Let us assume that there exists a constant  such that
such that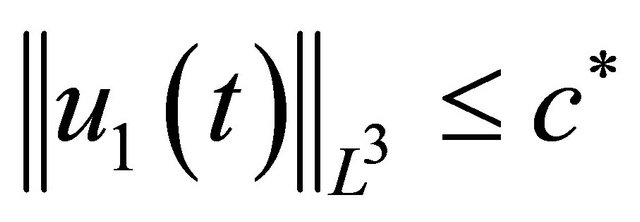 . Then
. Then
 (2.2)
(2.2)
for some absolute constant c > 0, where 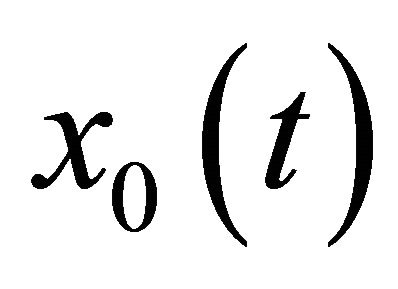 is a stance function such that
is a stance function such that

We recall, an “exterior” estimate, usable to radially symmetric functions only, originally due to [11]:
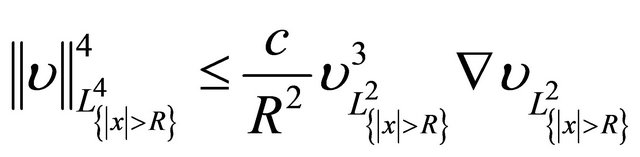 (2.3)
(2.3)
where c is independent of R > 0. We recall the generally usable symmetric functions and for any function 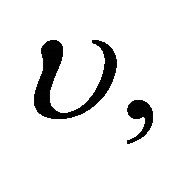
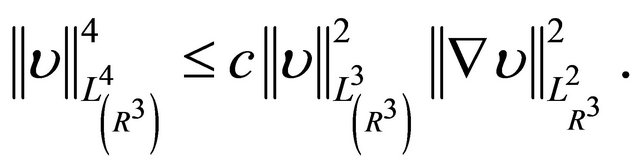 (2.4)
(2.4)
(2.3), (2.4) are Gagliardo-Nirenberg estimates for functions on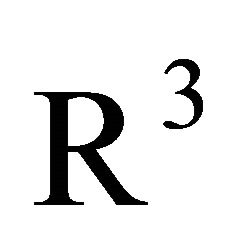 .
.
Proof of Prop 2.1: Since by (1.3), 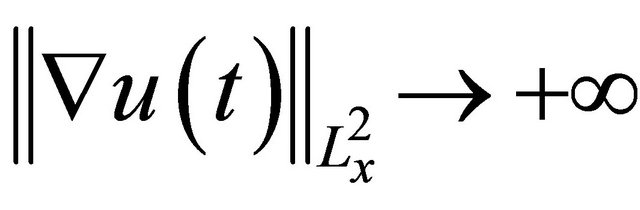 as
as 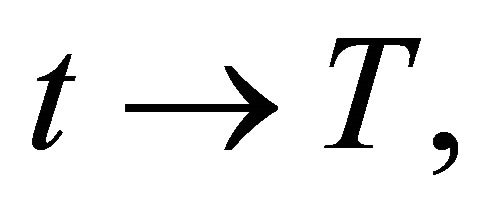 by energy conservation, we have
by energy conservation, we have
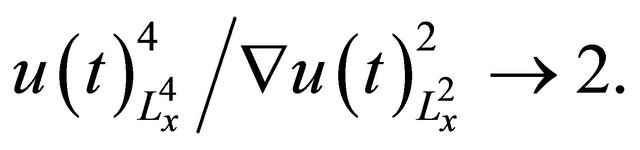 Thus, for t to be large enough to close to T
Thus, for t to be large enough to close to T
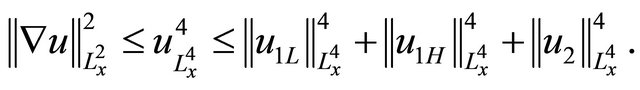 (2.5)
(2.5)
By (2.3), the selection of 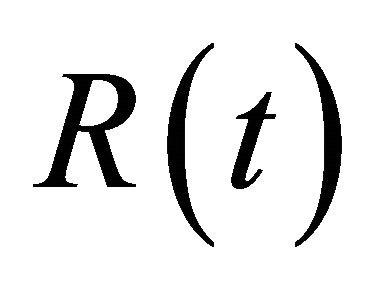 and mass conservation;
and mass conservation;
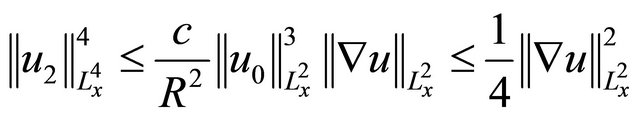 (2.6)
(2.6)
where c1 in the definition of 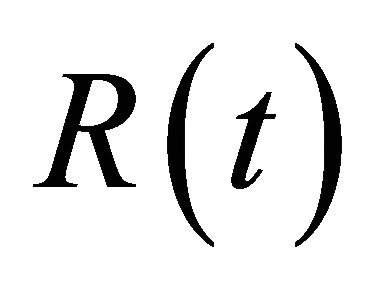 has been selected to obtain the factor
has been selected to obtain the factor  here. By Sobolev embedding, (1.10), and the selected
here. By Sobolev embedding, (1.10), and the selected 
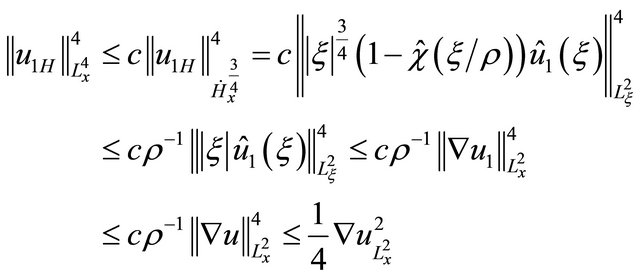 (2.7)
(2.7)
where c2 in the definition of  has been selected to obtain the factor
has been selected to obtain the factor  here. Bring together (2.5), (2.6), and (2.7), to obtain
here. Bring together (2.5), (2.6), and (2.7), to obtain
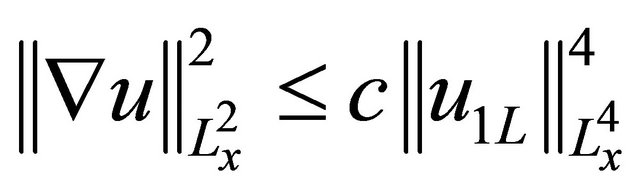 (2.8)
(2.8)
By (2.8) and (2.4), we obtain (2.1), completing the proof of part (1) of the proposition.
To prove part (2), we assume  by (2.8)
by (2.8)
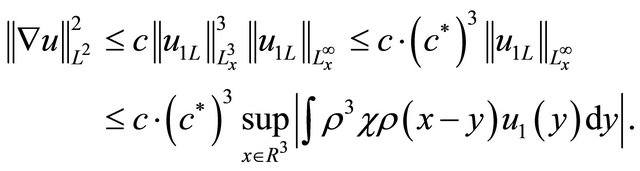
There exists  for which at least
for which at least  of this supremum is attained. Thus,
of this supremum is attained. Thus,

where we used Hölder’s inequality in the last step. By the selected , we obtain (2.2). To complete the proof, it keeps to obtain the remind control on
, we obtain (2.2). To complete the proof, it keeps to obtain the remind control on  which will be a consequence of the radial supposition and the supposed bound
which will be a consequence of the radial supposition and the supposed bound 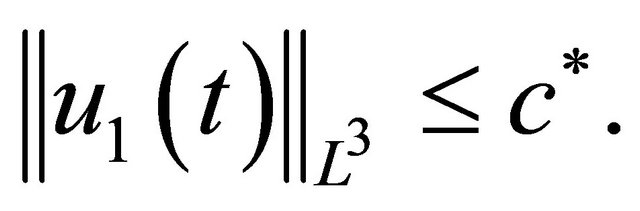
Assume 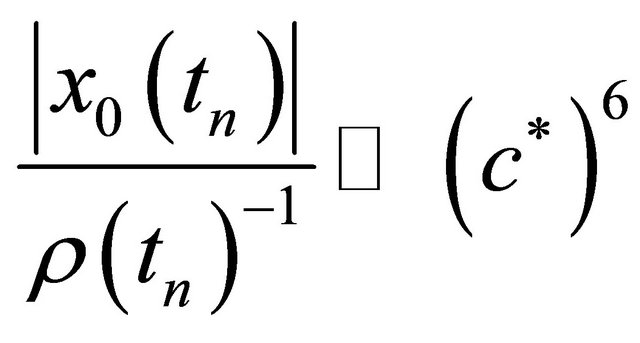 along a sequence of times
along a sequence of times  Assume the spherical annulus;
Assume the spherical annulus;
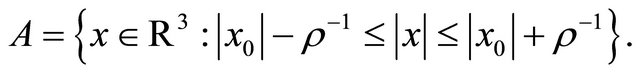
And inside A place 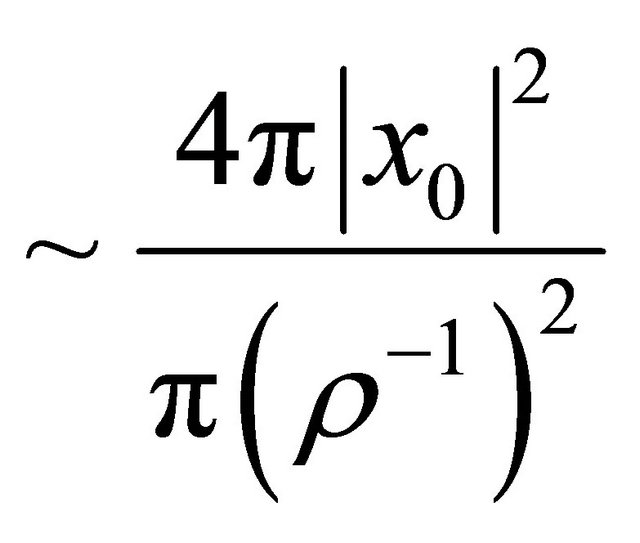 disjoint balls, at radius
disjoint balls, at radius 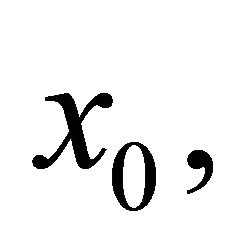 both the radius
both the radius , centered on the sphere. By the radiality supposition, on all ball B, we have
, centered on the sphere. By the radiality supposition, on all ball B, we have
 , and hence on the annulus A,
, and hence on the annulus A,
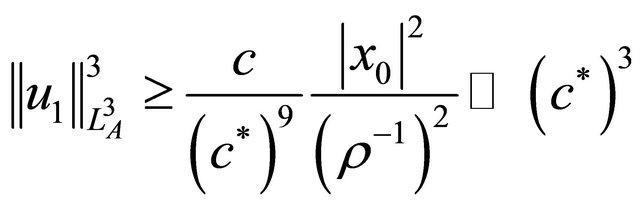 .
.
which contradicts the assumption .
. 
We now point out how to obtain Theorem 1.2 as a consequence.
Proof of Theorem 1.2. By part (1) of Prop. 2.1 and the standard convolution inequality:
 .
.
If 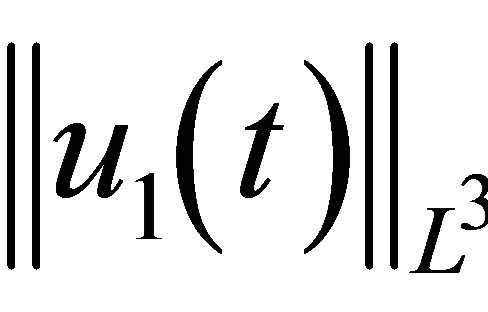 is not bounded, then there exists a sequence of times
is not bounded, then there exists a sequence of times  such that
such that  Since
Since
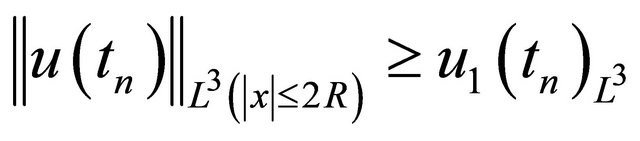 , we have (1.8) in Theorem 1.2;
, we have (1.8) in Theorem 1.2;
on the other hand, if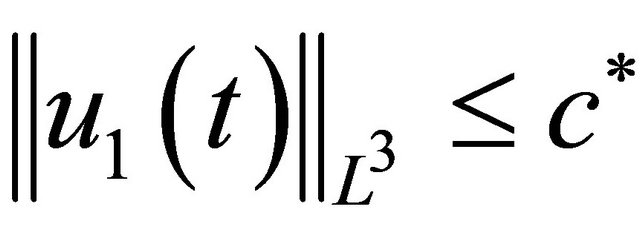 , for some c*, as t ® Twe have (2.2) of Prop. 2.1. Since
, for some c*, as t ® Twe have (2.2) of Prop. 2.1. Since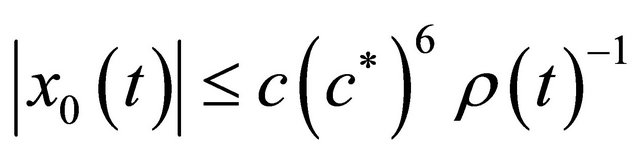 , we have
, we have

which gives (1.7) in Theorem 1.2. 
3. Strichartz Estimates
In this section we show local theory and Strichartz estimates.
Strichartz Type Estimates
We say the pair 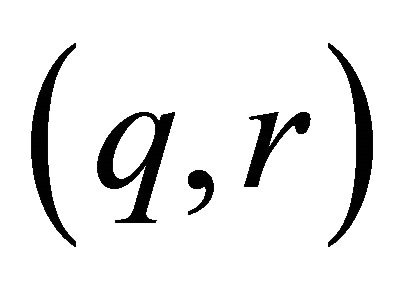 is
is  Strichartz admissible if
Strichartz admissible if
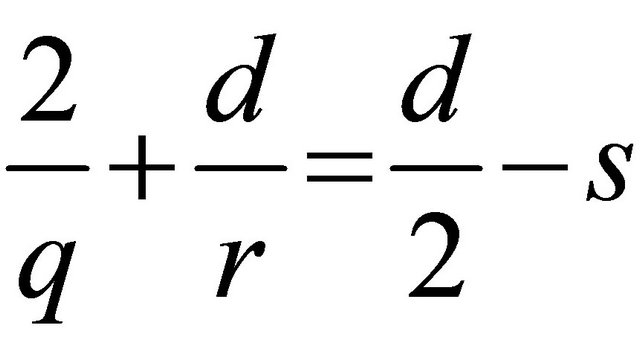 , with
, with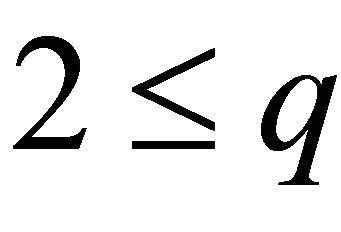 ,
,  and
and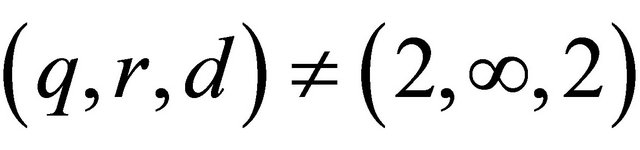 . And the pair
. And the pair 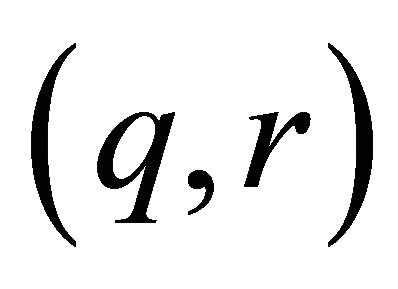 is
is 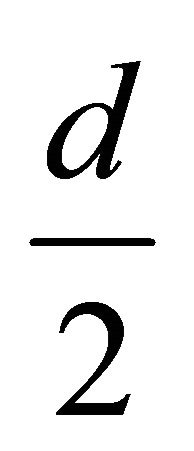 -passable if
-passable if ,
,  ,
, 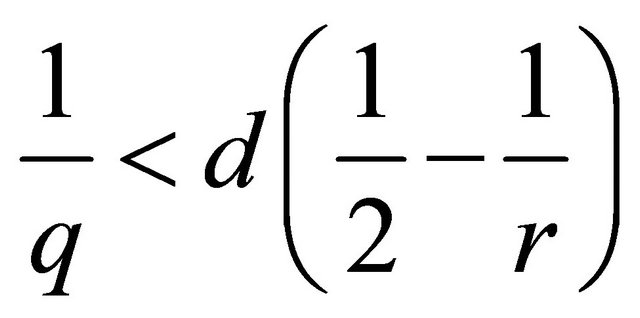 or
or .
.
As habitual we denote by 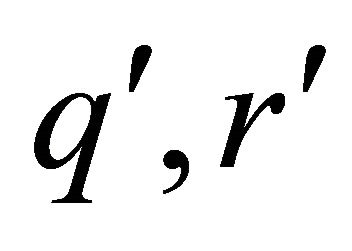 the Hölder conjugates of q and r consecutive (i.e.
the Hölder conjugates of q and r consecutive (i.e. ).
).
Let
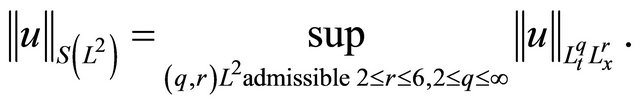
We consider dual Strichartz norms. Let
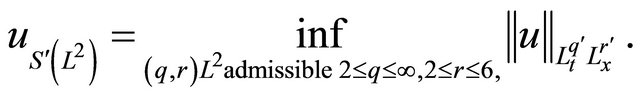
where 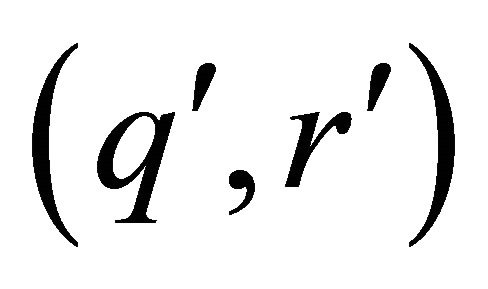 is the Hölder dual to
is the Hölder dual to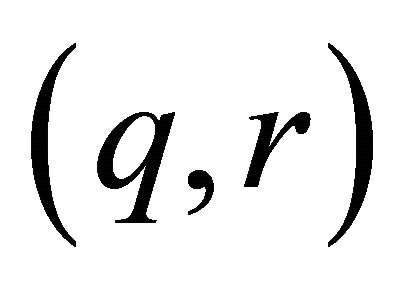 . Also define
. Also define

The Strichartz estimates are:
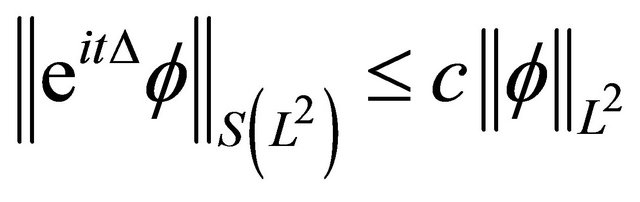
and
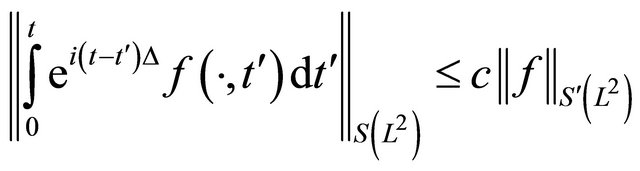 .
.
By bring together Sobolev embedding with the Strichartz estimates, we obtain
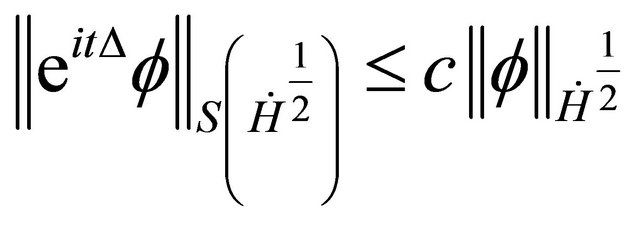
and
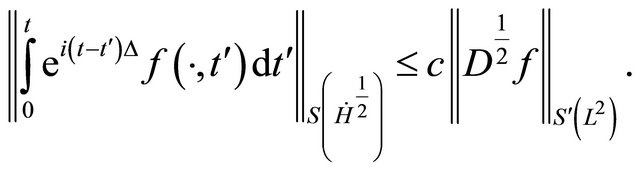 (3.1)
(3.1)
We must also need the Kato inhomogeneous Strichartz estimate [12].
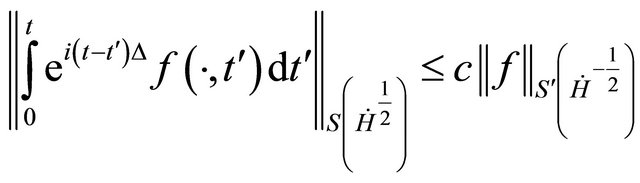 . (3.2)
. (3.2)
To point out a restriction to a time subinterval 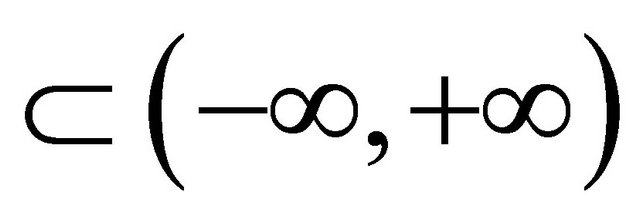 , we will write
, we will write 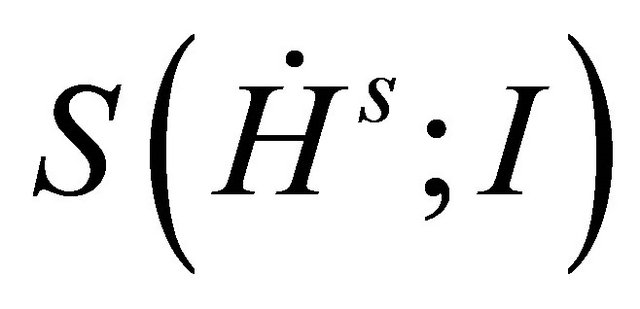 or
or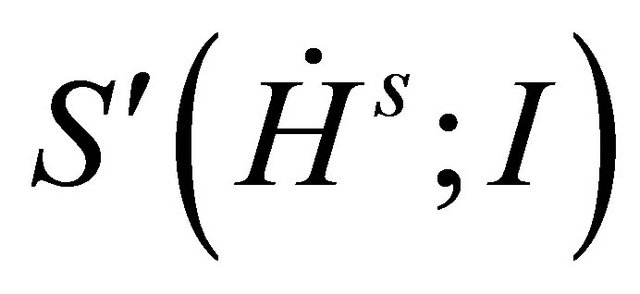 .
.
Proposition 3.1 Assume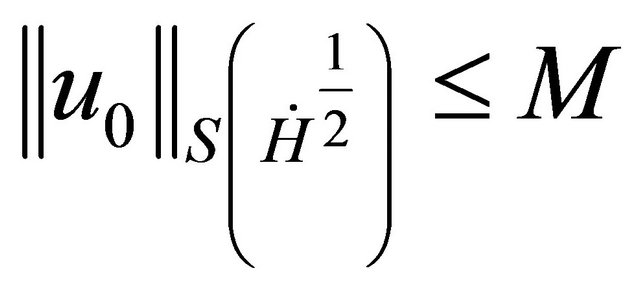 . There is
. There is 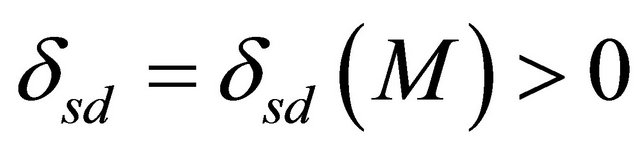 such that if
such that if , then u solving (1.1) is global (in
, then u solving (1.1) is global (in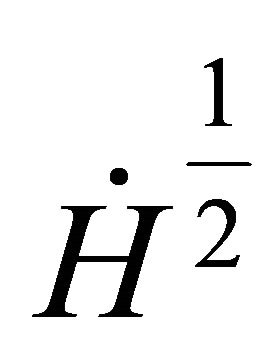 ) and
) and
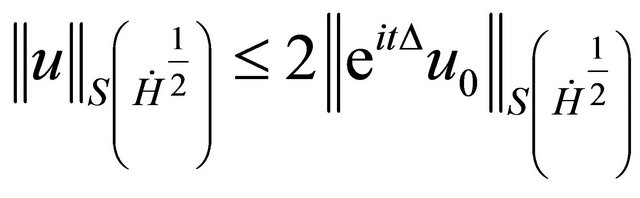 ,
,
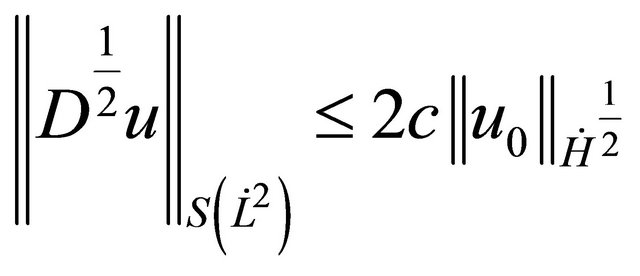 .
.
(Observe that, by the Strichartz estimates, the assumptions are satisfied if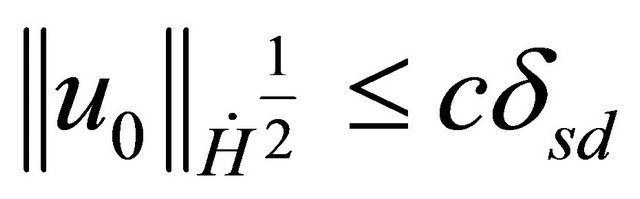 ).
).
Proof. Define
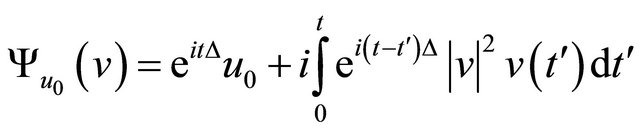 .
.
Applying the Strichartz estimates, we obtained
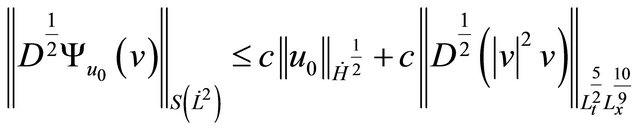
and
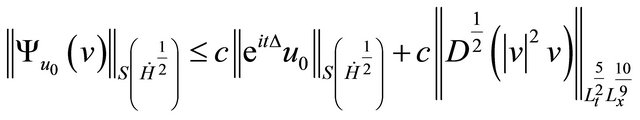
We apply the Hölder inequalities and fractional Leibnitz [13] to get

Let
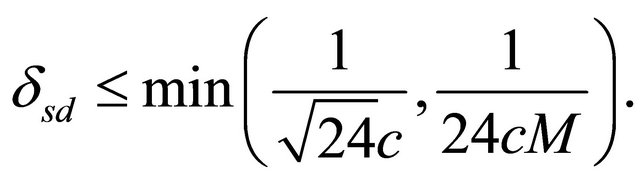
Then  where
where
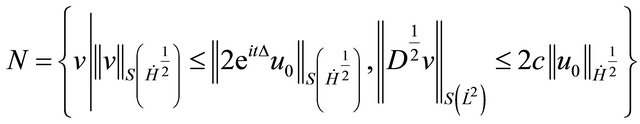
and 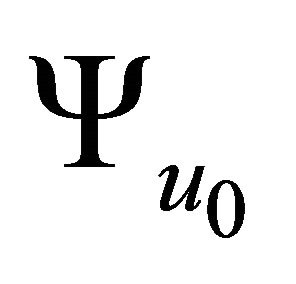 is a contraction on N.
is a contraction on N. 
Proposition 3.2. If 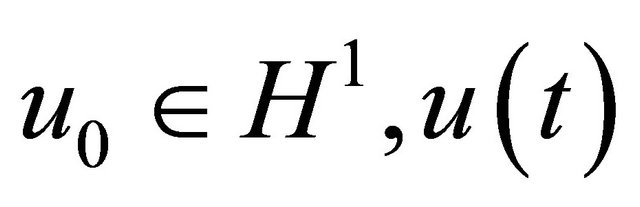 is global with globally finite
is global with globally finite  Strichartz norm
Strichartz norm 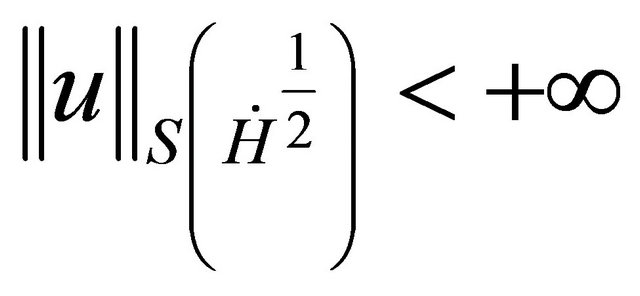 and a uniformly bounded H1 norm
and a uniformly bounded H1 norm 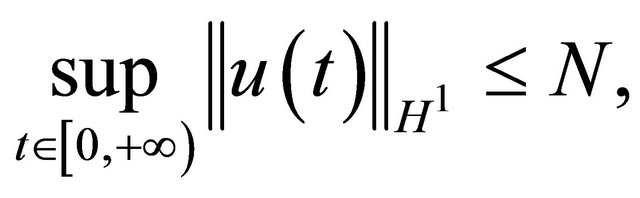 then
then 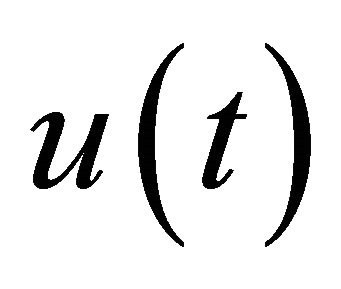 scatters in H1 as
scatters in H1 as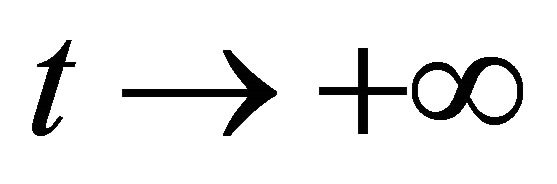 .
.
Meaning that there exist 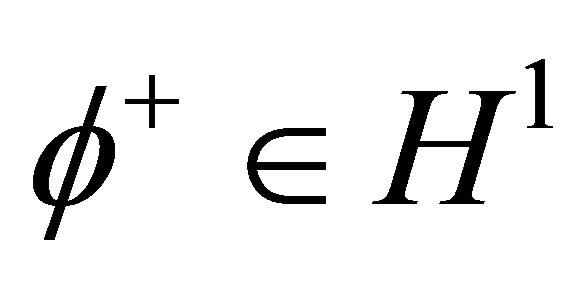 such that
such that
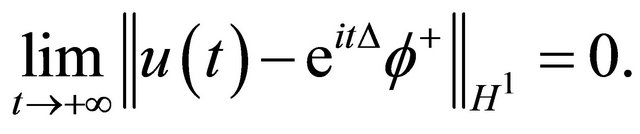
Proof. Since 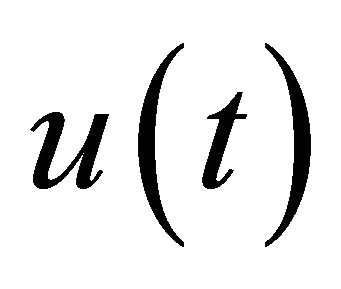 resolves the integral equation
resolves the integral equation
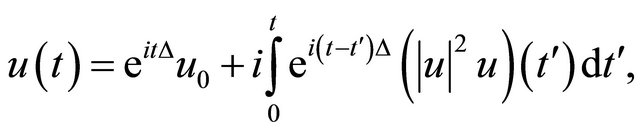
we have
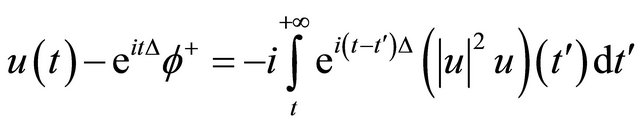 (3.3)
(3.3)
where
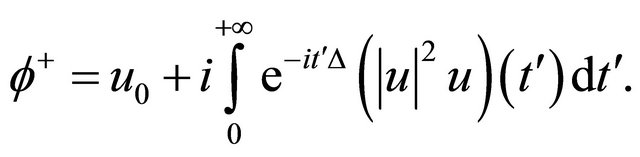
Apply the Strichartz estimates to (3.3), to get
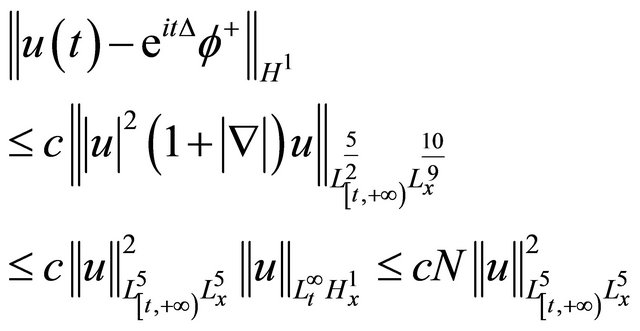
As  above inequality get the claim.
above inequality get the claim. 
4. Some Lemma
4.1. Here We Discuss the Precompactness of the Flow Implies Regular Localization
Let u be a solution to (1.1) such that
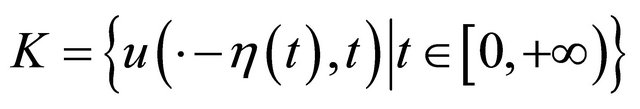 (4.1)
(4.1)
is precompact in H1. Then for each 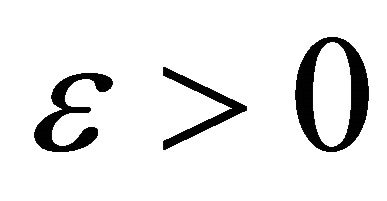 there exist R > 0 so that
there exist R > 0 so that  for all
for all 
We proof (4.2) by contradiction, there exists 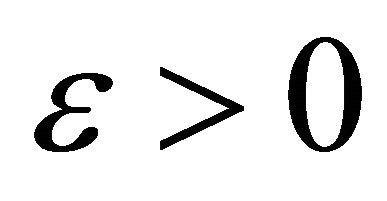 and a sequence of times
and a sequence of times 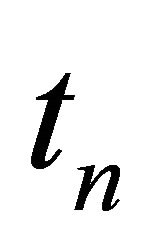 and by changing the variables,
and by changing the variables,
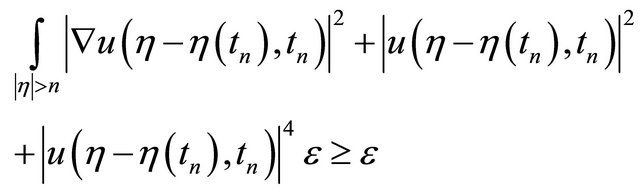 (4.3)
(4.3)
Since K is precompact, there exists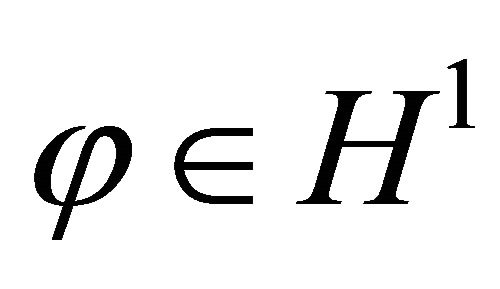 , such that
, such that 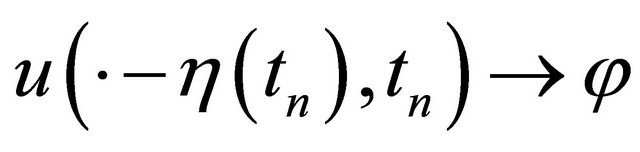 in H1, by (4.3),
in H1, by (4.3),

Which is a contradiction with the fact that 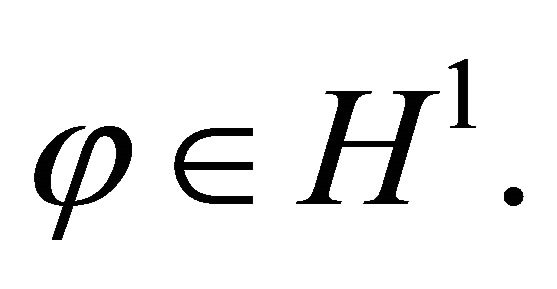 The proof is complete.
The proof is complete.
Lemma 4.1. Let u be a solution of (1.1) defined on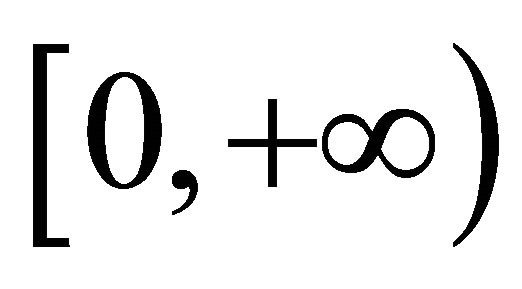 , such that
, such that 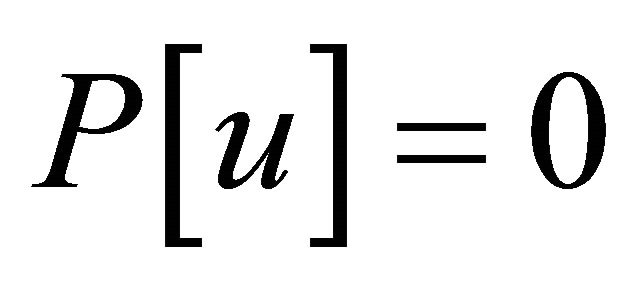 and K such as in (4.1) is precompact in H1, for some continuous function
and K such as in (4.1) is precompact in H1, for some continuous function 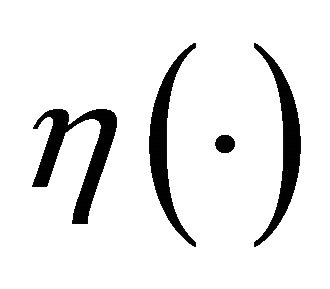 then;
then;
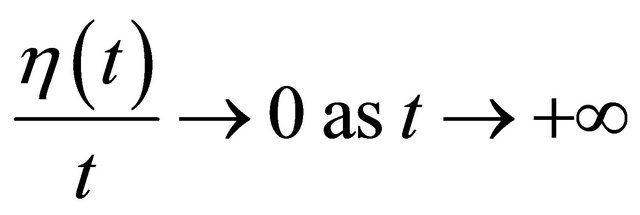 (4.4)
(4.4)
Proof. Suppose that (4.4) does not hold. Then there exists a sequence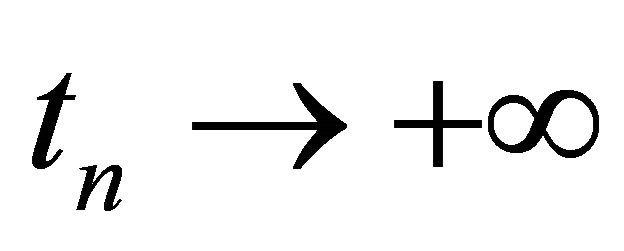 , such that
, such that 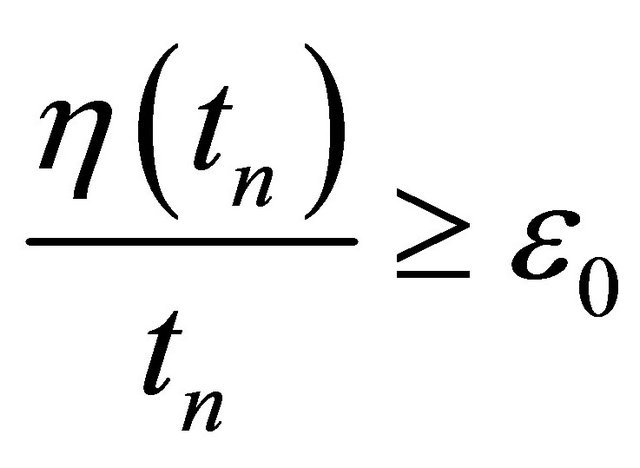 for some ε0 > 0. Retaining generality, we assume
for some ε0 > 0. Retaining generality, we assume 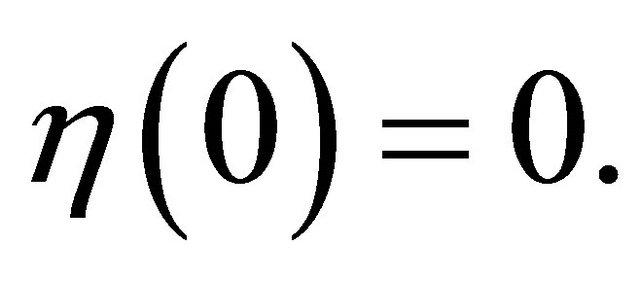 For R > 0, let
For R > 0, let
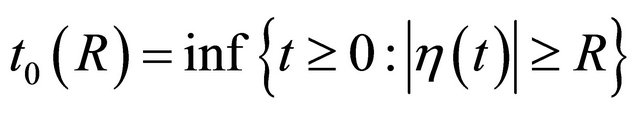
i.e. 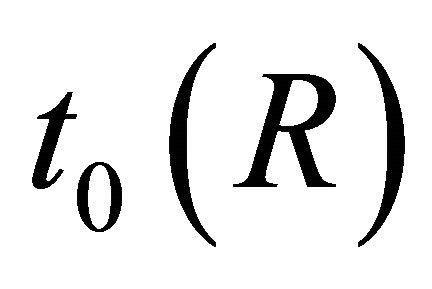 is the first time when
is the first time when 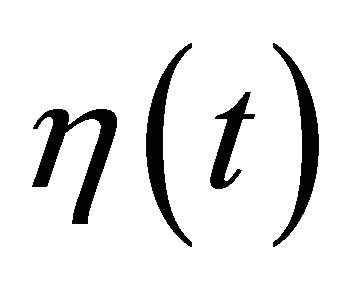 arrives at the boundary of the ball of radius R. By continuity of
arrives at the boundary of the ball of radius R. By continuity of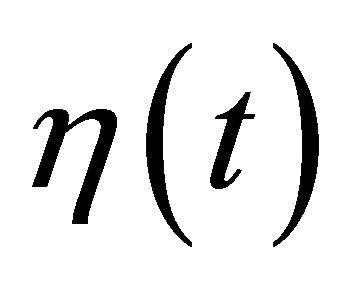 , the value
, the value 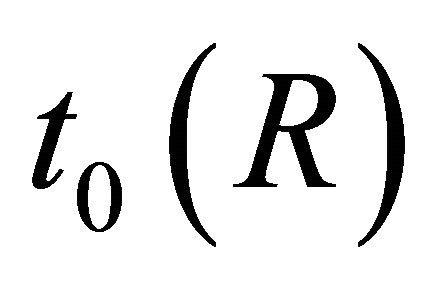 is well-defined. Furthermore, the following hold:
is well-defined. Furthermore, the following hold:
1) 
2) 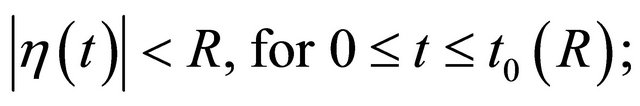
3)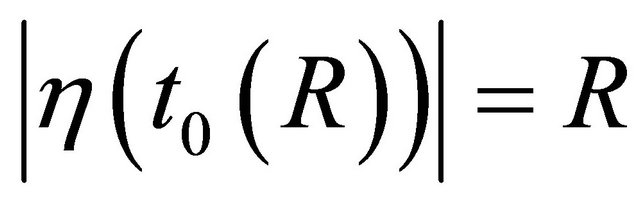 .
.
Let  and
and 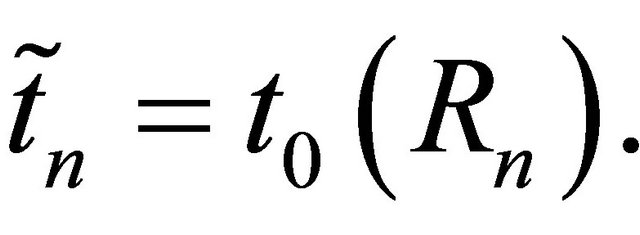 We note that
We note that , which combined with
, which combined with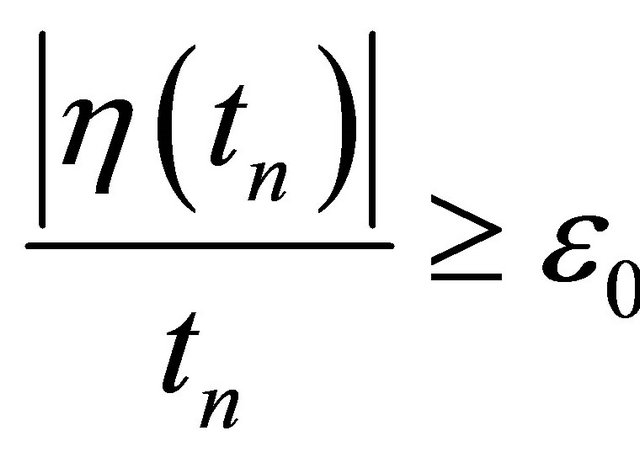 , gives
, gives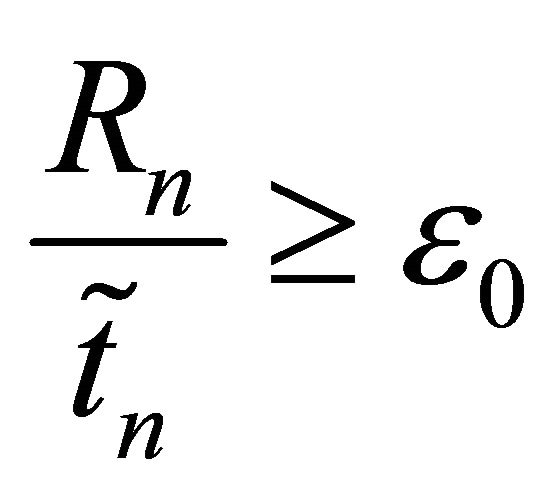 . Since
. Since 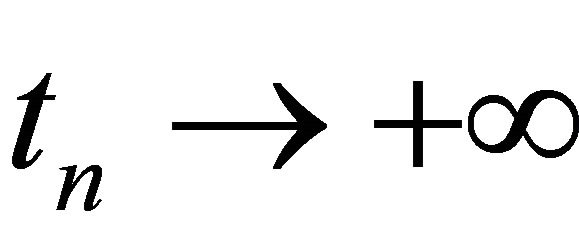 and
and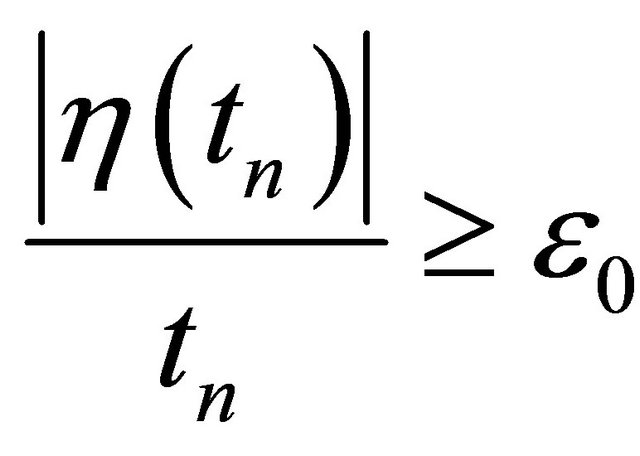 , we have
, we have 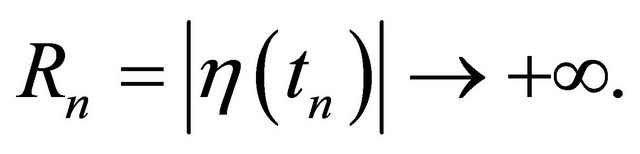 Thus
Thus 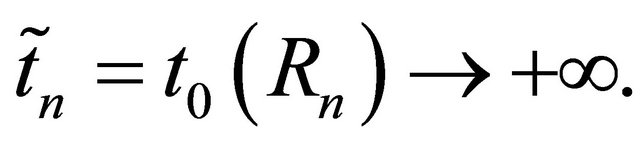 We can disregard
We can disregard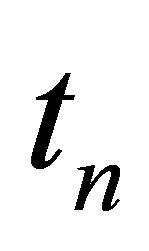 . We will concentrate our work on the time interval
. We will concentrate our work on the time interval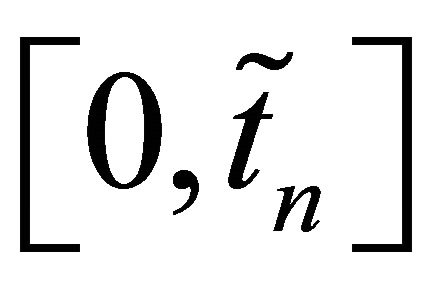 , and we will use in the proof:
, and we will use in the proof:
1) 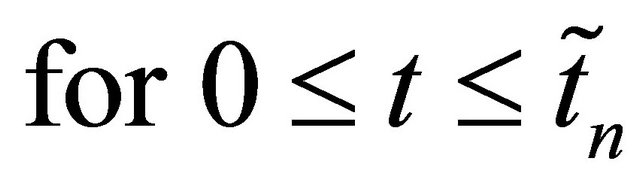 we have
we have 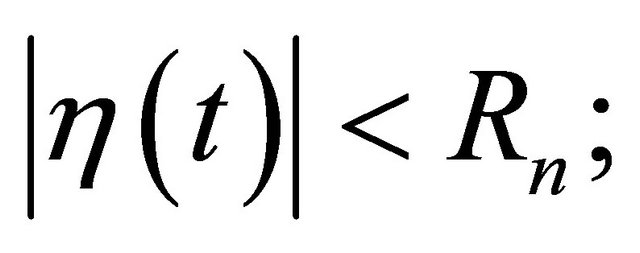
2) 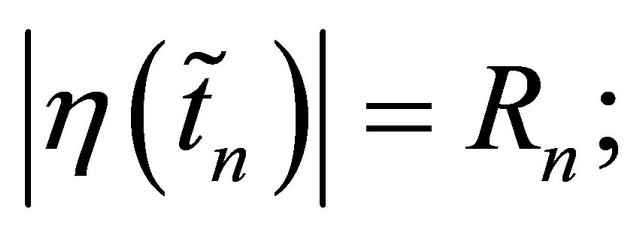
3) 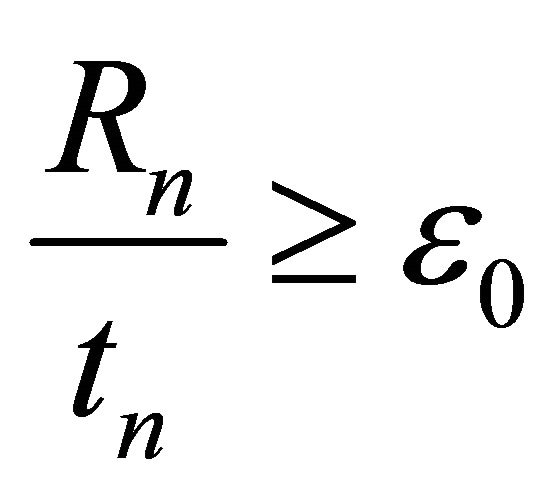 and
and 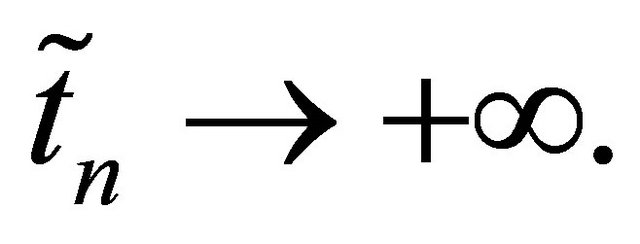
By the precompactness of K and (4.2) it follows that for any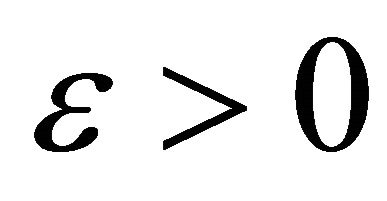 , there exists
, there exists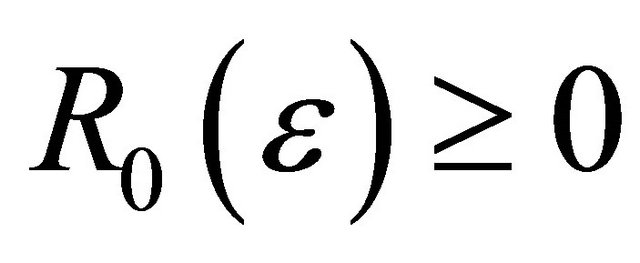 , such that for any
, such that for any 
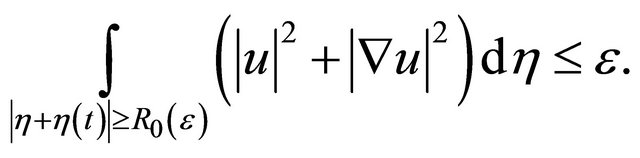 (4.5)
(4.5)
We will select ε later; for  let
let 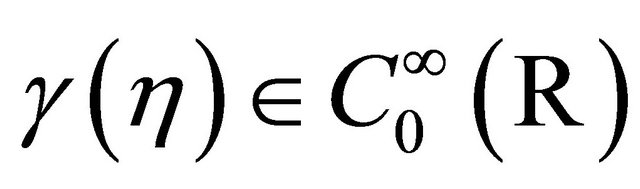 be such that
be such that  for
for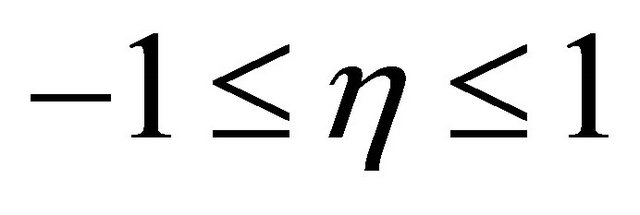 ,
, 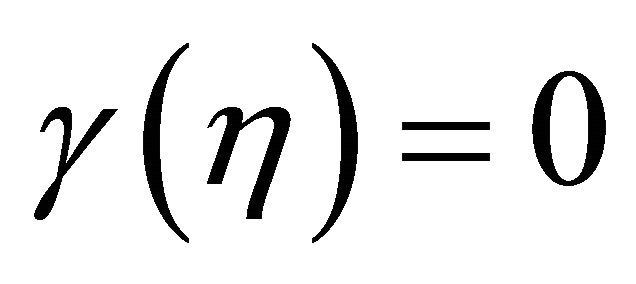 for
for
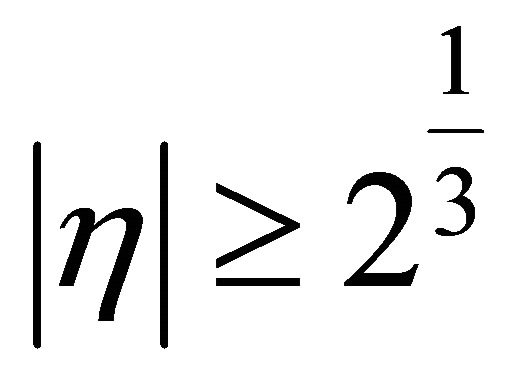 ,
,  ,
,  and
and 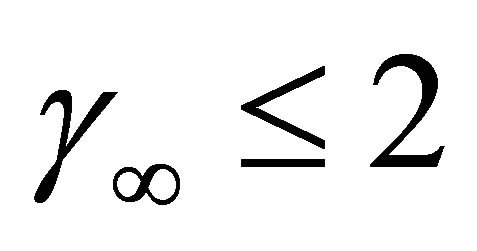 for
for
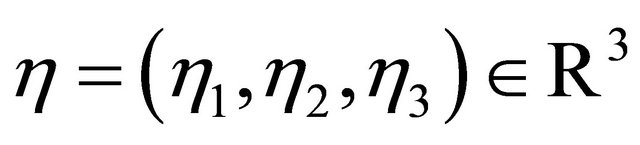 . Let
. Let 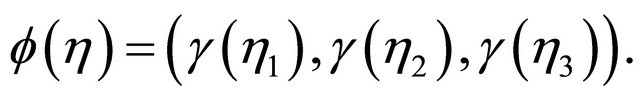
Then 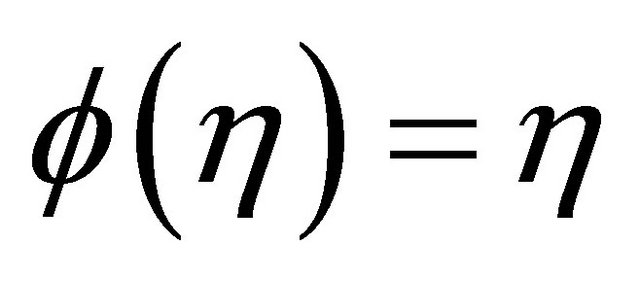 for
for 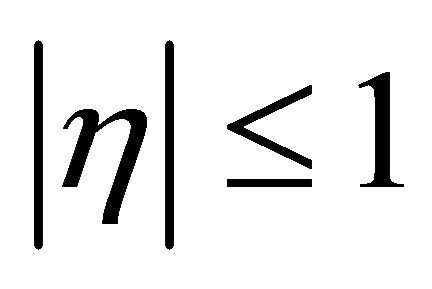 and
and 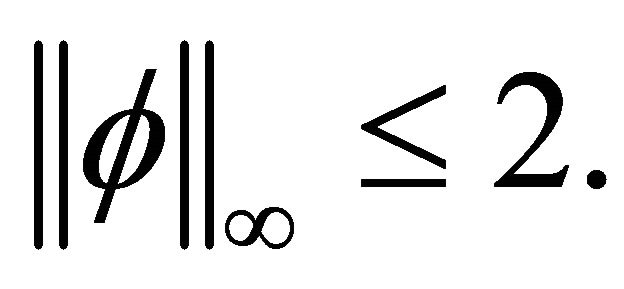 For R > 0, set
For R > 0, set  Let
Let  be the truncation center of mass given by
be the truncation center of mass given by

Then , where
, where

Observe that 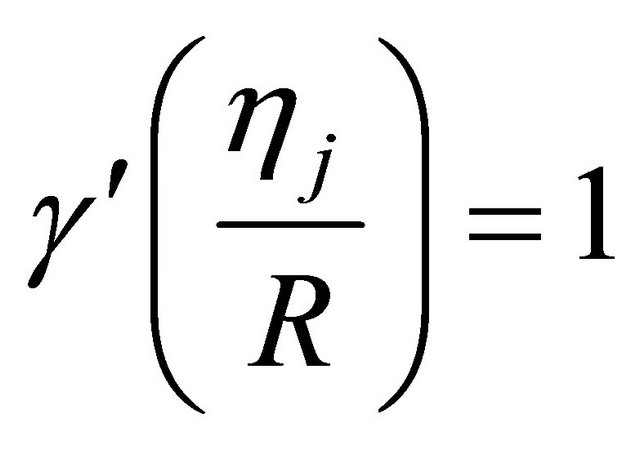 for
for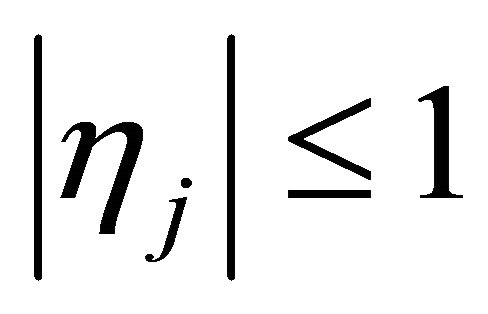 . By the zero momentum property
. By the zero momentum property
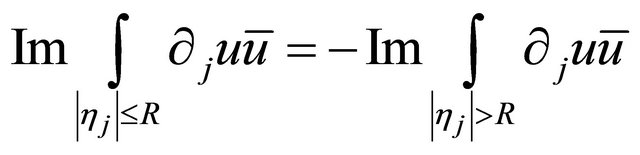 .
.
Thus,
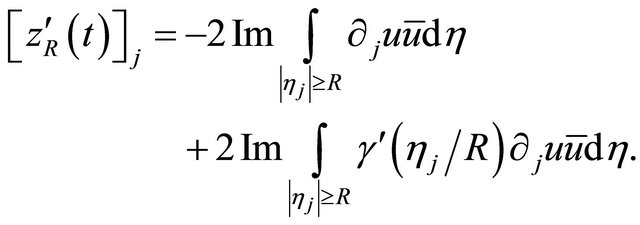
By Cauchy-Schwarz, we obtain;
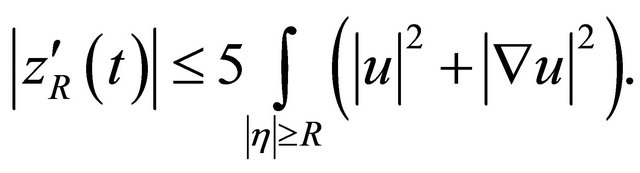 (4.6)
(4.6)
Set 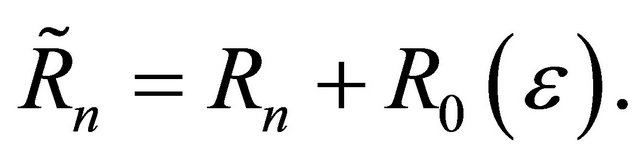 Observe that for
Observe that for 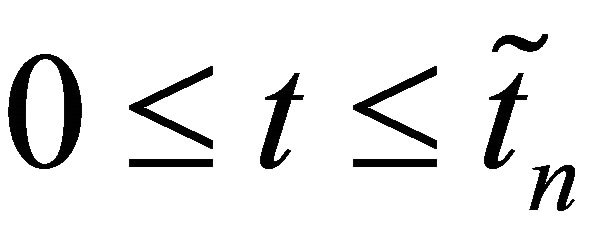 and
and
 , we have
, we have , and thus
, and thus
(4.6), (4.5) give
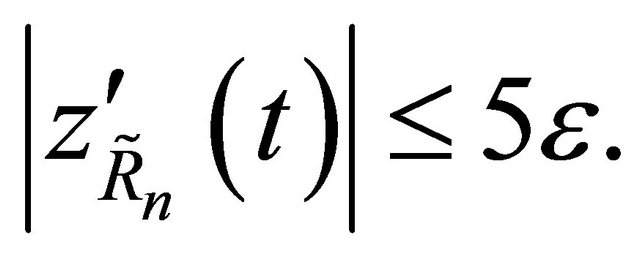 (4.7)
(4.7)
We now obtain an upper bound for  and a lower bound for
and a lower bound for 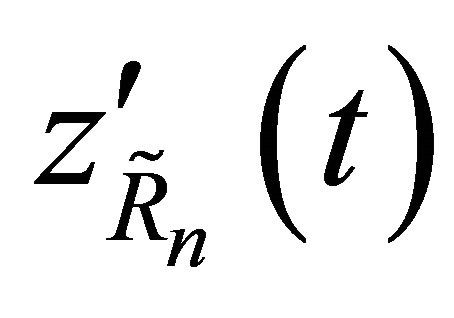
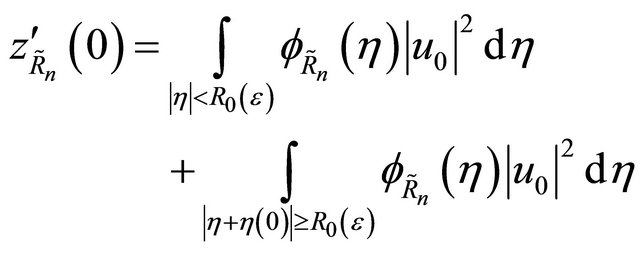
Hence, by (4.5) we have
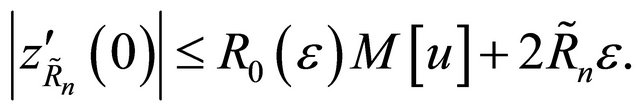 (4.8)
(4.8)
For , we divide
, we divide 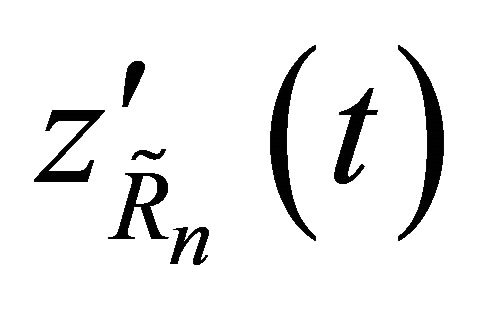 as
as
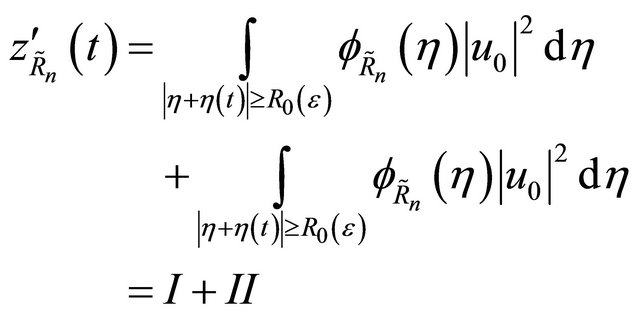
To deduce the expression for I, we observed that 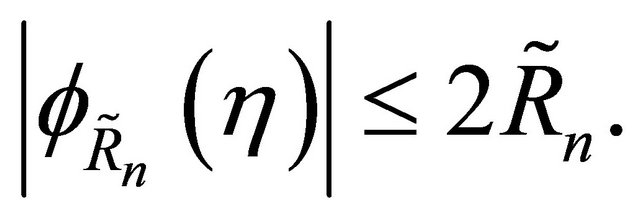
And use (4.5) to obtain 
For II we first observe that,
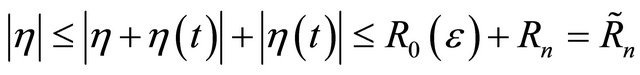
and thus 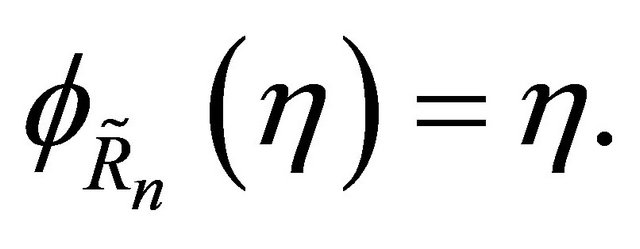
We rewrite II as
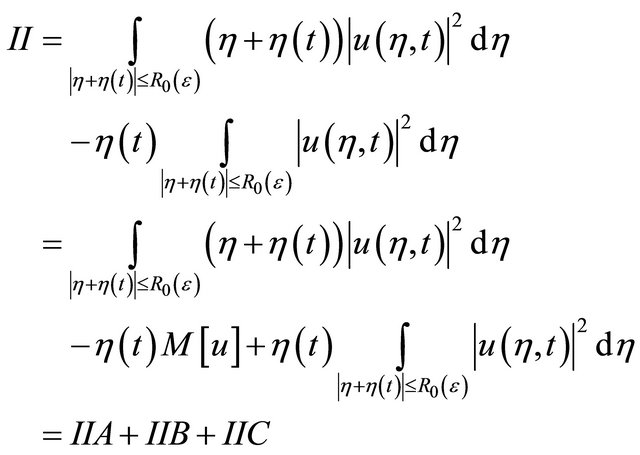
Trivially, 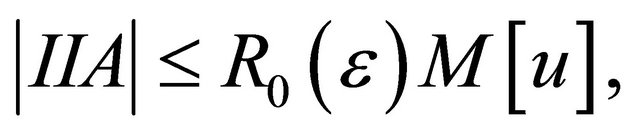 and by (4.5)
and by (4.5)
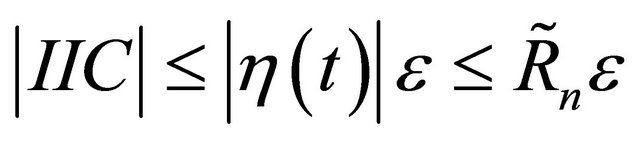 .
.
Thus,
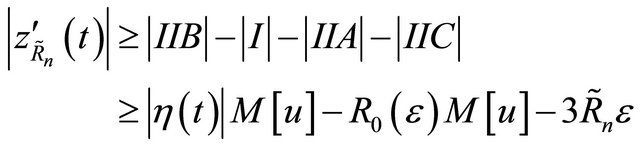
Taking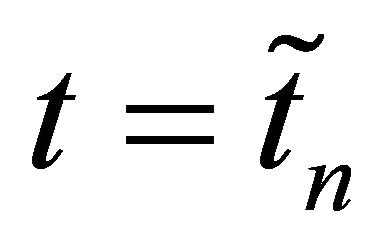 , we can get
, we can get
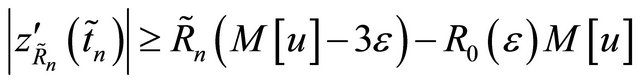 (4.9)
(4.9)
Combining (4.7), (4.8), and (4.9), we have
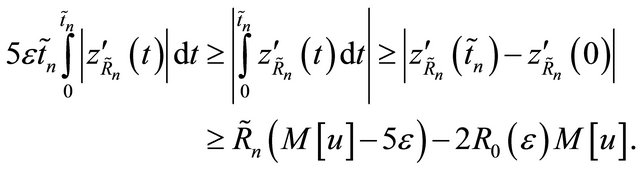
Suppose  and use
and use 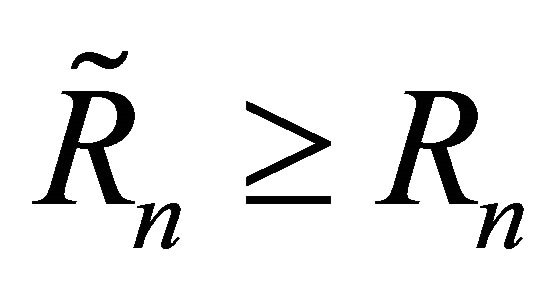 to obtain
to obtain
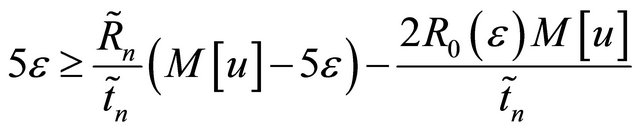
Since  we have
we have
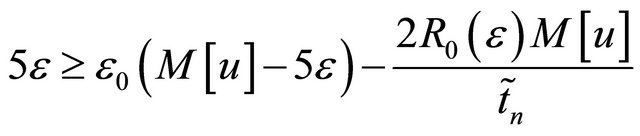
(Assume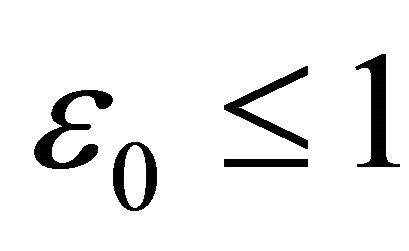 ) take
) take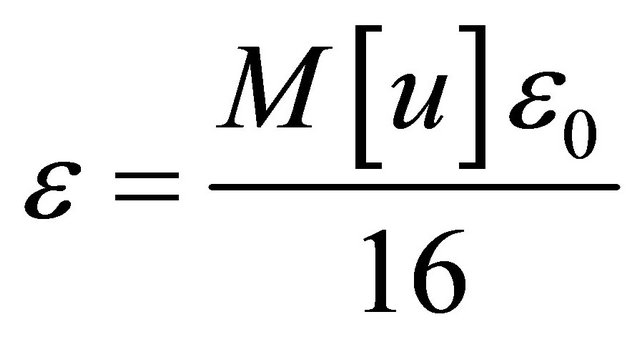 , as
, as 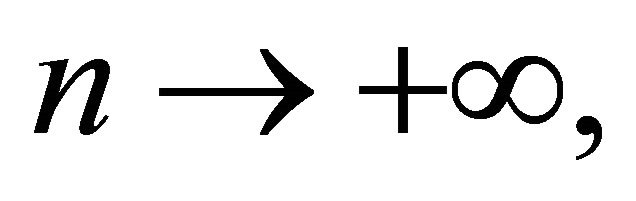 since
since  we get a contradiction.
we get a contradiction. 
4.2. We Now Prove the Following Rigidity Theorem
Lemma 4.2. If (1.5) and (1.6) hold, then for all t
 (4.10)
(4.10)
where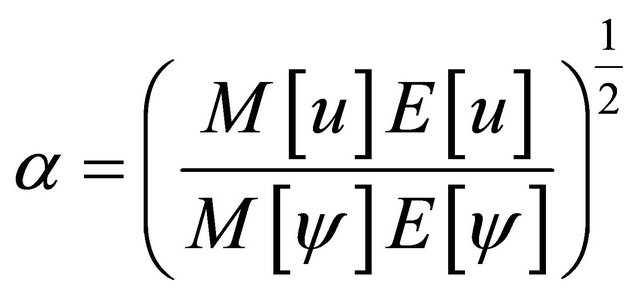 . We have also the bound for all t;
. We have also the bound for all t;
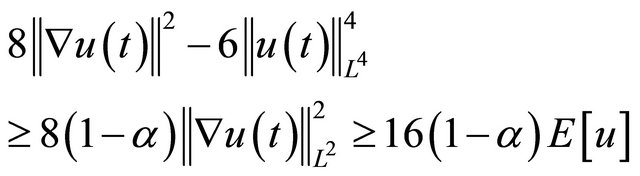 (4.11)
(4.11)
The hypothesis here is 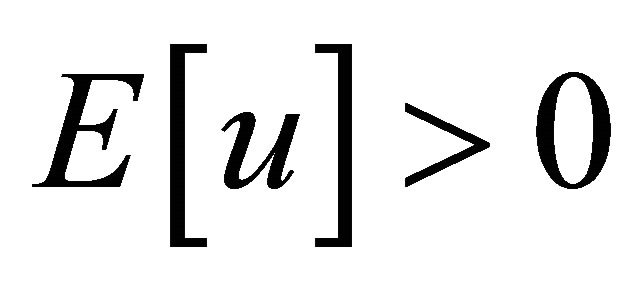 except if
except if 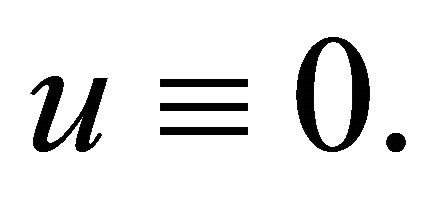 In fact,
In fact, 
Theorem 4.3. Assume 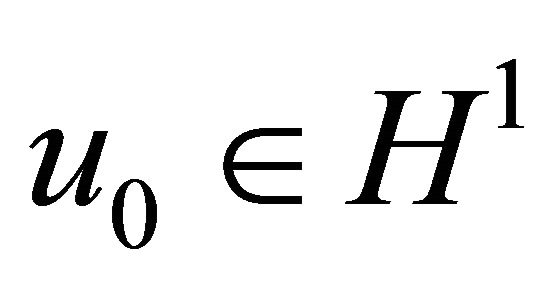 satisfies
satisfies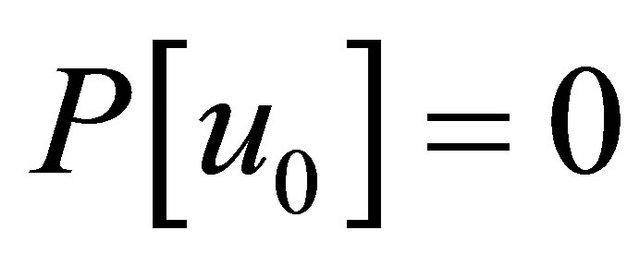 ,
,
 (4.12)
(4.12)
and
 (4.13)
(4.13)
Let u be the global H1 solution of (1.1) with initial data u0 and assume that 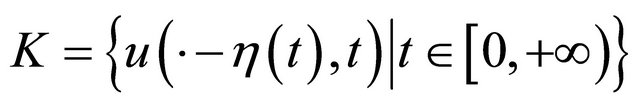 is precompact in H1. Then
is precompact in H1. Then  .
.
Proof. Let  be redial with
be redial with
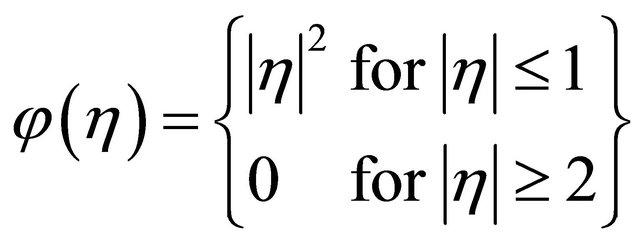 .
.
For R > 0, we define
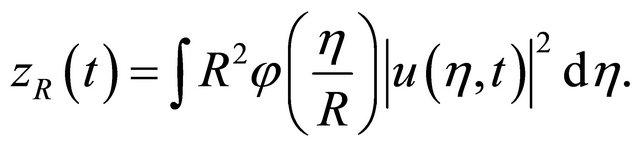
Then
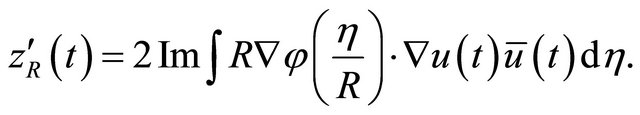
By the Hölder inequality:
 (4.14)
(4.14)
By calculation, we have the local Virial identity
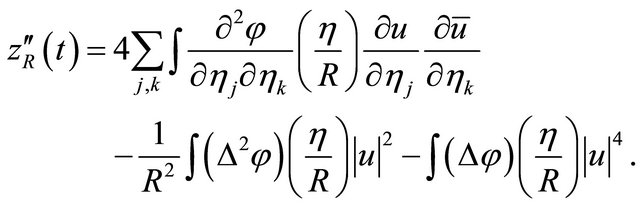
Since  is radial we have
is radial we have
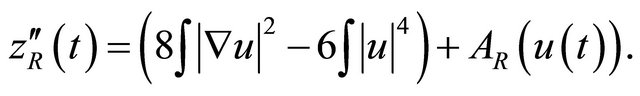 (4.15)
(4.15)
where
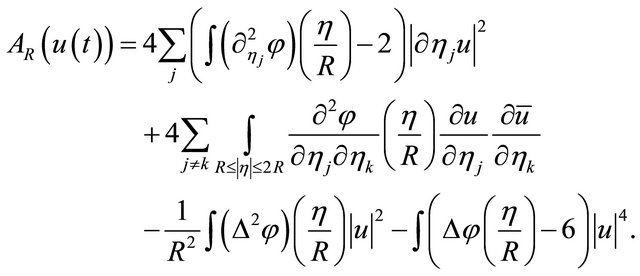
Thus, we obtain
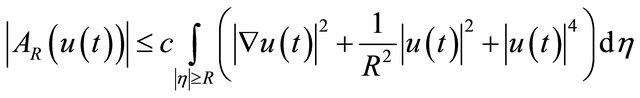 (4.16)
(4.16)
Now discuss 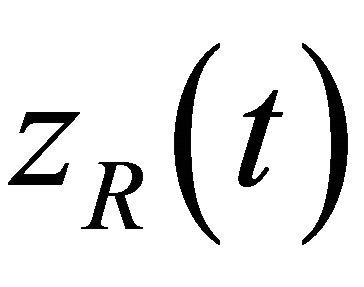 for R chosen appropriate large and selection time interval
for R chosen appropriate large and selection time interval 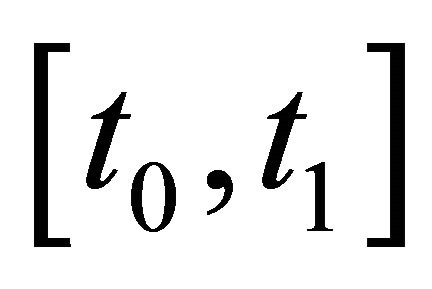 where
where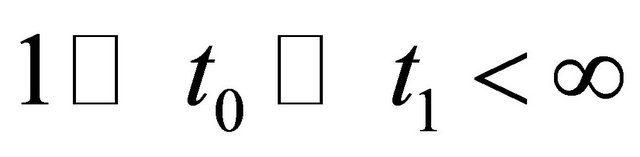 . By (4.15) and (4.11) we have
. By (4.15) and (4.11) we have
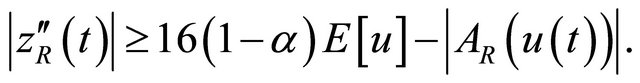 (4.17)
(4.17)
Set 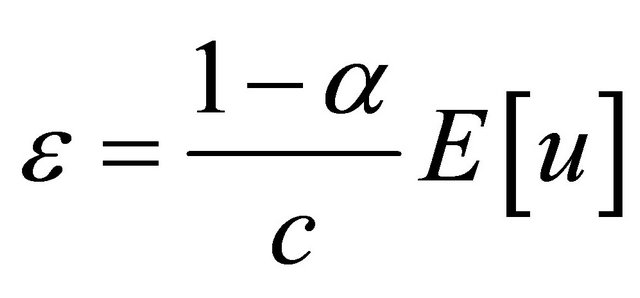 in (4.2),
in (4.2), 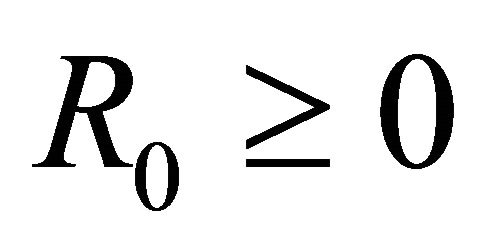 , such that
, such that 
 (4.18)
(4.18)
Choosing 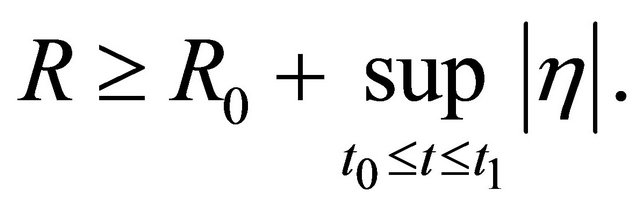 Then (4.16), (4.17) and
Then (4.16), (4.17) and
(4.18) imply that for all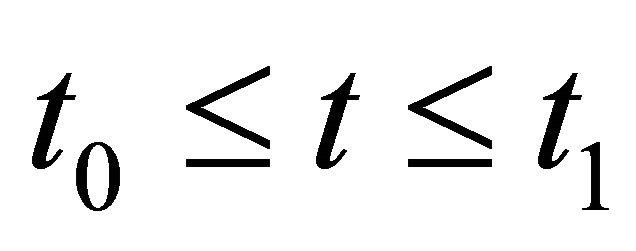 ,
,
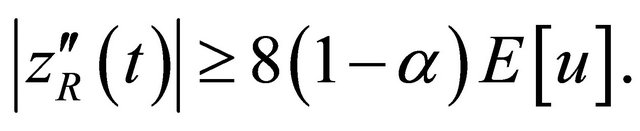 (4.19)
(4.19)
By Lemma 4.1, there exists 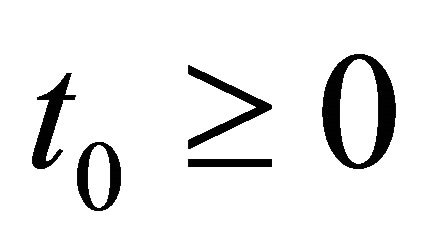 such that for all
such that for all 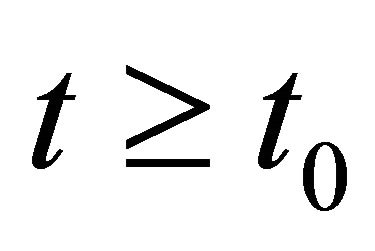 we have
we have 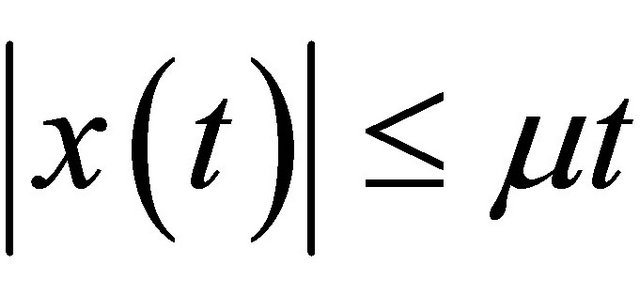 with
with  By taking R =
By taking R =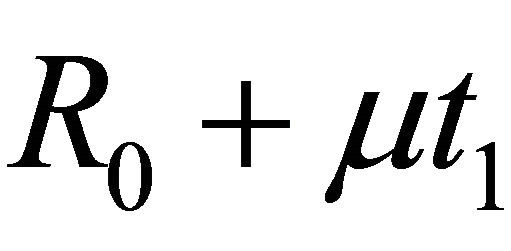 , we obtain that (4.18) holds for all
, we obtain that (4.18) holds for all 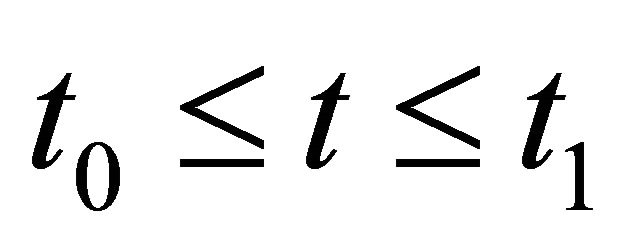 . Integrating (4.19) over
. Integrating (4.19) over  we obtain
we obtain
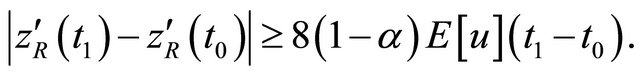 (4.20)
(4.20)
On the other hand, for all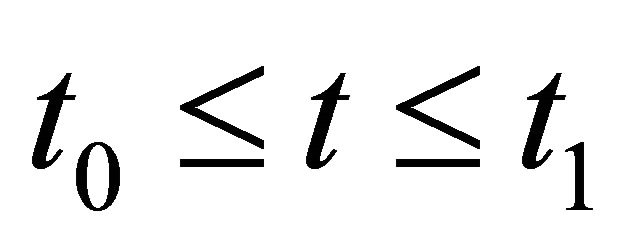 , by (4.10) and (4.14), we have
, by (4.10) and (4.14), we have
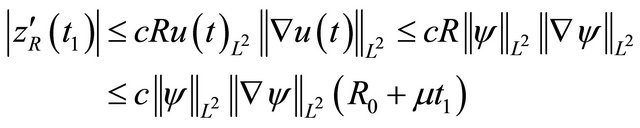 (4.21)
(4.21)
Combining (4.20) and (4. 21), we obtained
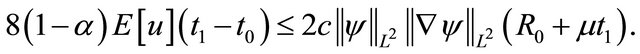
It is important to mention that  and
and 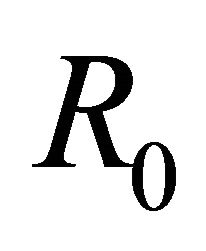 are constant depending only on
are constant depending only on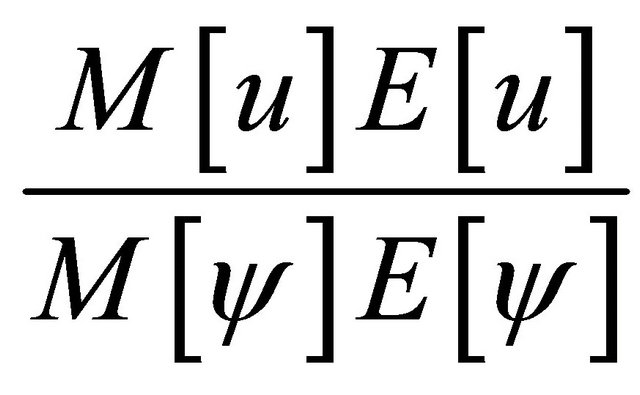 , and
, and .
.
Putting 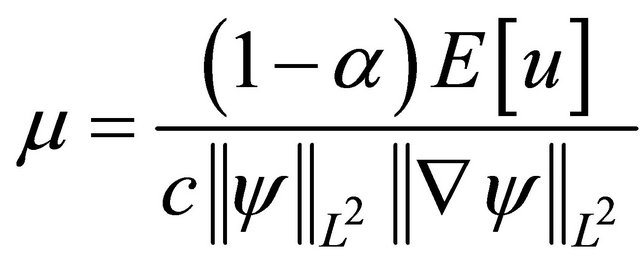 and setting
and setting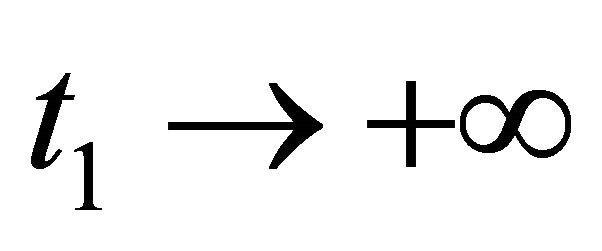 , we obtain a contradiction except if
, we obtain a contradiction except if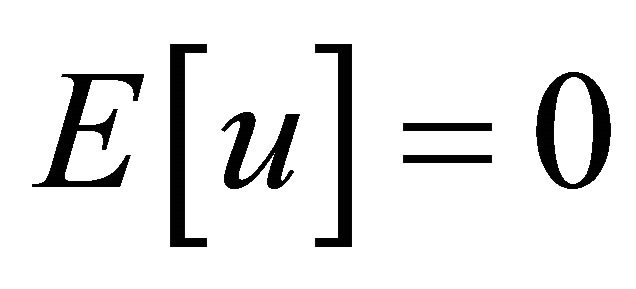 , which implies
, which implies 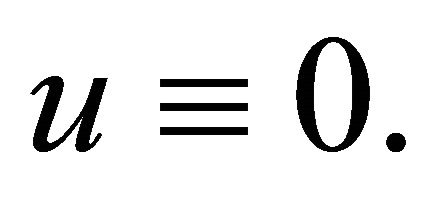

REFERENCES
- T. T. Tao, “On the Asymptotic Behavior of Large Radial Data for a Focusing Non-Linear Schrödinger Equation,” Dynamics of Partial Differential Equations, Vol. 1, No. 1, 2004, pp. 1-48.
- T. Tao, “A (Concentration-)Compact Attractor for High- Dimensional Non-Linear Schrödinger Equation,” Dynamics of Partial Differential Equations, Vol. 4, No. 1, 2007, pp. 1-53.
- T. Cazenave, “Semilinear Schrödinger Equations. Courant Lecture Notes in Mathematics,” New York University, Courant Institute of Mathematical Sciences, New York, American Mathematical Society, Providence, 2003.
- T. Tao, “Nonlinear Dispersive Equations: Local and Global Analysis,” CBMS Regional Conference Series in Mathematics, Published for the Conference Board of the Mathematical Sciences, Washington DC, American Mathematical Society, Providence, 2006.
- M. Weinstein, “Nonlinear Schrödinger Equations and Sharp Interpolation Estimates,” Communications in Mathematical Physics, Vol. 87, No. 4, 1982, pp. 567-576.
- J. Holmer and S. Roudenko, “A Sharp Condition for Scattering of the Radial 3D Cubic Nonlinear Schrödinger Equations,” Communications in Mathematical Physics, Vol. 282, No. 2, 2008, pp. 435-467.
- C. E. Kenig and F. Merle, “Global Well-Posedness, Scattering, and Blow-Up for the Energy-Critical Focusing Nonlinear Schrödinger Equation in the Radial Case,” Inventiones Mathematicae, Vo. 166, No. 3, 2006, pp. 645- 675.
- J. Colliander, M. Keel, G. Staffilani, H. Takaoka and T. Tao, “Global Existence and Scattering for Rough Solutions of a Nonlinear Schrödinger Equation on R3,” Communications on Pure and Applied Mathematics, Vol. 57, No. 8, 2004, pp. 987-1014.
- T. Hmidi and S. Keraani, “Blowup Theory for the Critical Nonlinear Schrödinger Equations Revisited,” International Mathematics Research Notices, Vol. 2005, No. 46, 2005, pp. 2815-2828. doi:10.1155/IMRN.2005.2815
- F. Merle and Y. Tsutsumi, “L2 Concentration of Blow-Up Solutions for the Nonlinear Schrödinger Equation with Critical Power Nonlinearity,” Journal of Differential Equations, Vol. 84, No. 2, 1990, pp. 205-214.
- W. A. Strauss, “Existence of Solitary Waves in Higher Dimensions,” Communications in Mathematical Physics, Vol. 55, No. 2, 1977, pp. 149-162.
- D. Foschi, “Inhomogeneous Strichartz Estimates,” J. Hyper. Diff. Eq., Vol. 2, No. 1, 2005, pp. 1-24.
- C. Kenig, G. Ponce and L. Vega, “Well-Posedness and Scattering Results for the Generalized Korteweg-De Vries Equation via the Contraction Principle,” Communications on Pure and Applied Mathematics, Vol. 46, No. 4, 1993, pp. 527-620.
- S. Keraani, “On the Defect of Compactness for the Strichartz Estimates of the Schrödinger Equation,” Journal of Differential Equations, Vol. 175, No. 2, 2001, pp. 353- 392. doi:10.1006/jdeq.2000.3951
- E. Donley, N. Claussen, S. Cornish, J. Roberts, E. Cornell and C. Wieman, “Dynamics of Collapsing and Exploding Bose-Einstein Condensates,” Nature, Vol. 412, No. 6844, 2001, pp. 295-299. doi:10.1038/35085500
- C. Sulem and P.-L. Sulem, “The Nonlinear Schrödinger Equation. Self-Focusing and Wave Collapse,” Applied Mathematical Sciences, Vol. 139, 1999.
- M. Vilela, “Regularity of Solutions to the Free Schrö- dinger Equation with Radial Initial Data,” Illinois Journal of Mathematics, Vol. 45, No. 2, 2001, pp. 361-370.
- L. Bergé, T. Alexander and Y. Kivshar, “Stability Criterion for Attractive Bose-Einstein Condensates,” Physical Review A, Vol. 62, No. 2, 2000, 6 p.
- P. Bégout, “Necessary Conditions and Sufficient Conditions for Global Existence in the Nonlinear Schrödinger Equation,” Advances in Applied Mathematics and Mechanics, Vol. 12, No. 2, 2002, pp. 817-827.

