Advances in Pure Mathematics
Vol.2 No.5(2012), Article ID:22797,4 pages DOI:10.4236/apm.2012.25043
Existence of a Nontrivial Solution for a Class of Superquadratic Elliptic Problems*
1Department of Biotechnology, Beijing City University, Beijing, China
2School of Mathematics and Statistics, Central South University, Changsha, China
3Employee’s College of Dongcheng in Beijing, Beijing, China
4School of Mathematical Sciences, Qufu Normal University, Qufu, China
Email: #maoam@163.com
Received May 17, 2012; revised June 20, 2012; accepted June 28, 2012
Keywords: Elliptic problems; Local Linking theorem; 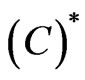 condition; Superquadratic
condition; Superquadratic
ABSTRACT
We consider the existence of a nontrivial solution for the Dirichlet boundary value problem
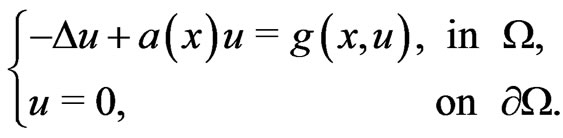
We prove an abstract result on the existence of a critical point for the functional  on a Hilbert space via the local linking theorem. Different from the works in the literature, the new theorem is constructed under the
on a Hilbert space via the local linking theorem. Different from the works in the literature, the new theorem is constructed under the 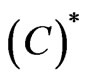 condition instead of
condition instead of 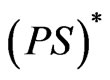 condition.
condition.
1. Introduction and Main Results
Consider the Dirichlet boundary value problem
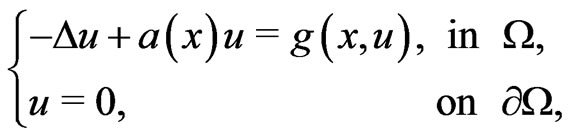 (1)
(1)
where 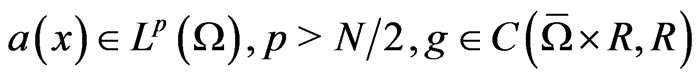 and
and  is a bounded domain whose boundary is a smooth manifold.
is a bounded domain whose boundary is a smooth manifold.
We assume that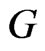 , where
, where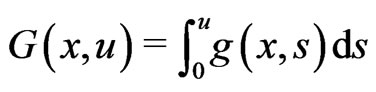 . In [1], Li and Willem established the existence of a nontrivial solution for problem (1) under the following well-known Ambrosetti-Rabinowitz superlinearity condition: there exists
. In [1], Li and Willem established the existence of a nontrivial solution for problem (1) under the following well-known Ambrosetti-Rabinowitz superlinearity condition: there exists 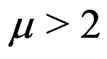 and
and 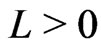 such that
such that
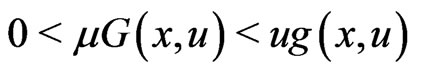 (AR)
(AR)
for all 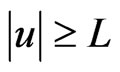 and
and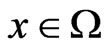 , which has been used extensively in the literature; see [1-4] and the references therein. It is easy to see that condition (AR) does not include some superquadratic nonlinearity like
, which has been used extensively in the literature; see [1-4] and the references therein. It is easy to see that condition (AR) does not include some superquadratic nonlinearity like
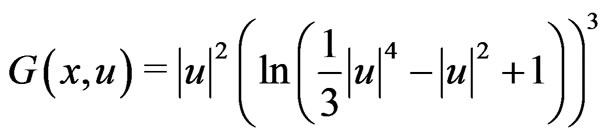 (G0)
(G0)
In [5], Qin Jiang and Chunlei Tang completed the Theorem 4 in [1], and obtained the existence of a nontrivial solution for problem (1) under a new superquadratic condition which covered the case of (G0). The conditions are as follows:
(G1) , as
, as  uniformly on
uniformly on (G2)
(G2)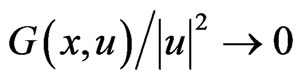 , as
, as 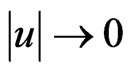 uniformly on
uniformly on (G3) There are constants
(G3) There are constants 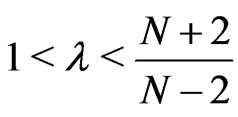 and
and 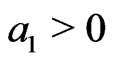
such that

for all (G4) There are constants
(G4) There are constants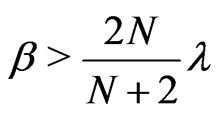 ,
, 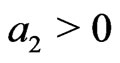 and
and
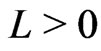 such that
such that
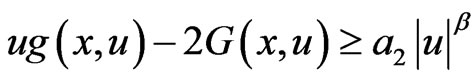
for all 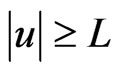 and
and If 0 is an eigenvalue of
If 0 is an eigenvalue of 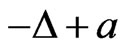 (with Dirichlet boundary condition) assume also the condition that:
(with Dirichlet boundary condition) assume also the condition that:
(G5) There exists 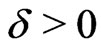 such that:
such that:
1)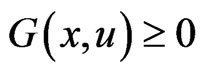 , for all
, for all ,
,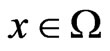 ; or 2)
; or 2)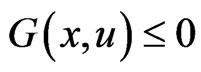 , for all
, for all ,
,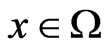 .
.
Note that (G4) is also (AR) type condition.
The aim of this paper is to consider the nontrivial solution of problem (1) in a more general sense. Without the Ambrosetti-Rabinowitz superlinearity condition (AR) or (G4), the superlinear problems become more complicated. We do not know in our situations whether the (PS) or 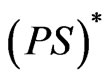 sequence are bounded. However, we can check that any Cerami (or
sequence are bounded. However, we can check that any Cerami (or ) sequence is bounded. The definition of
) sequence is bounded. The definition of  (or
(or ) sequence can be found in [6].
) sequence can be found in [6].
We will obtain the same conclusion under the  condition instead of
condition instead of  condition. So we only need the following conditions instead of (G3) (G4):
condition. So we only need the following conditions instead of (G3) (G4):
(G3') Let 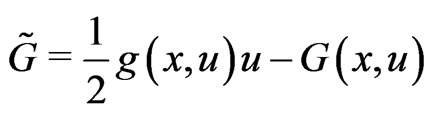 satisfying 1)
satisfying 1) 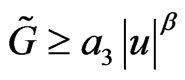 if
if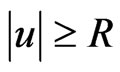 2)
2) 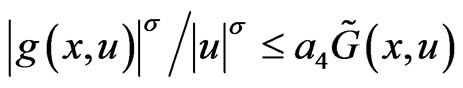 if
if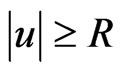 , where
, where
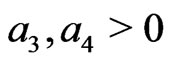 ,
, .
.
It is easy to see that function
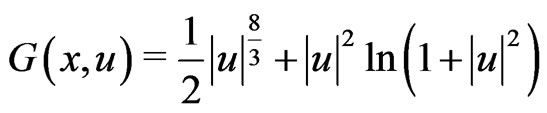
satisfies conditions of (G1) (G2) (G5) and (G3').
Our main result is the following theorem:
Theorem 1.1. Suppose that 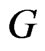 satisfies (G1) (G2) (G5) and (G3'). If 0 is an eigenvalue of
satisfies (G1) (G2) (G5) and (G3'). If 0 is an eigenvalue of 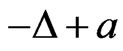 (with Dirichlet boundary condition). Then problem (1) has at least one nontrivial solution.
(with Dirichlet boundary condition). Then problem (1) has at least one nontrivial solution.
Remark 1. There are many functions which are superlinear but it is not necessary to satisfy AmbrosettiRabinowitz condition. For example,
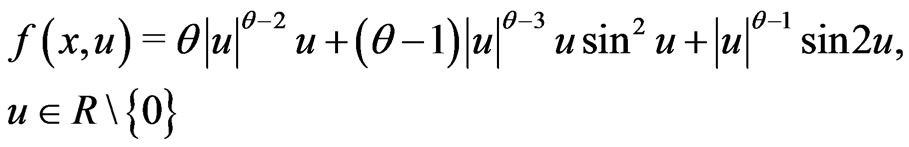
where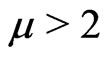 . Then it is easy to check that (AR) does not hold. On the other hand, in order to verify (AR), it usually is an annoying task to compute the primitive function of
. Then it is easy to check that (AR) does not hold. On the other hand, in order to verify (AR), it usually is an annoying task to compute the primitive function of  and sometimes it is almost impossible. For example,
and sometimes it is almost impossible. For example,
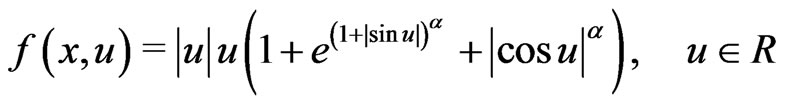
where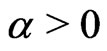 .
.
Remark 2. Our condition is much weaker than (AR) type condition (cf. [6]).
2. Proof of Theorem
Define a functional 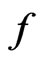 in the space
in the space 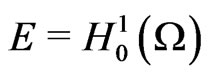 by
by
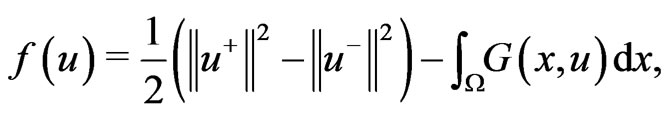
where ,
,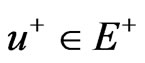 ,
, 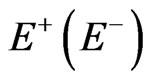 is the space spanned by the eigenvectors corresponding to negative (positive) eigenvalue of
is the space spanned by the eigenvectors corresponding to negative (positive) eigenvalue of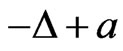 .
.
In this paper, we shall use the following local linking theorem (Lemma 2.1) to prove our Theorem . Let 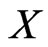 be a real Banach space with
be a real Banach space with 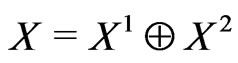 and
and 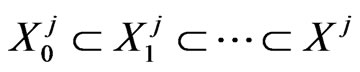 such that
such that ,
, 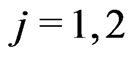 . For every multi-index
. For every multi-index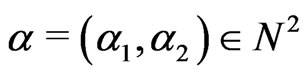 , let
, let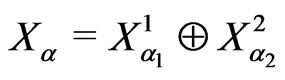 . We know that
. We know that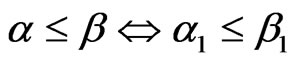 ,
,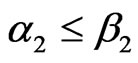 . A sequence
. A sequence 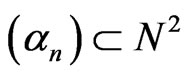 is admissible if for every
is admissible if for every 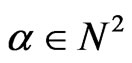 there is
there is 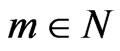 such that
such that 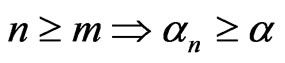 . We say
. We say  satisfies the
satisfies the  condition if every sequence
condition if every sequence 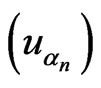 such that
such that  is admissible and satisfies
is admissible and satisfies

contains a subsequence which converges to a critical point of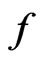 .
.
Lemma 2.1. ([6]) Suppose that 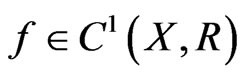 satisfies the following assumptions:
satisfies the following assumptions:
(f1) 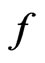 has a local linking at 0(f2)
has a local linking at 0(f2) 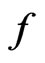 satisfies
satisfies 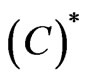 condition(f3)
condition(f3) 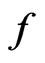 maps bounded sets into bounded sets(f4) For every
maps bounded sets into bounded sets(f4) For every ,
, 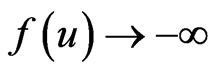 as
as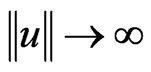 , on
, on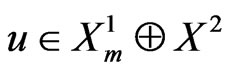 .
.
Then  has at least two critical points.
has at least two critical points.
Proof of Theorem 1. We shall apply Lemma 2.1 to the functional 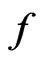 associated with (1), we consider the case where 0 is an eigenvalue of
associated with (1), we consider the case where 0 is an eigenvalue of 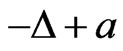 and
and
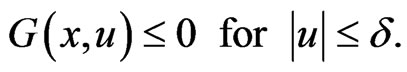 (2)
(2)
The other case are similar.
1) 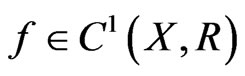 and
and  maps bounded sets into bounded sets.
maps bounded sets into bounded sets.
Let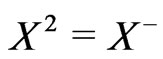 ,
,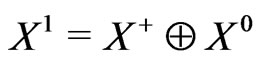 . Choose Hilbertian basis
. Choose Hilbertian basis 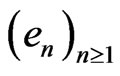 for
for 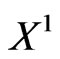 and
and 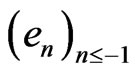 for
for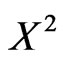 , define
, define
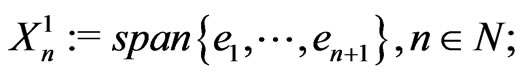
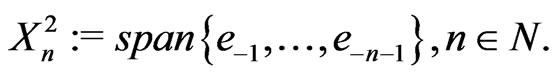
Assumption (G3') implies there are constants 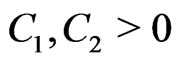 such that
such that
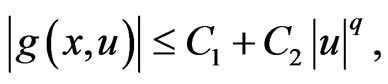 (3)
(3)
so
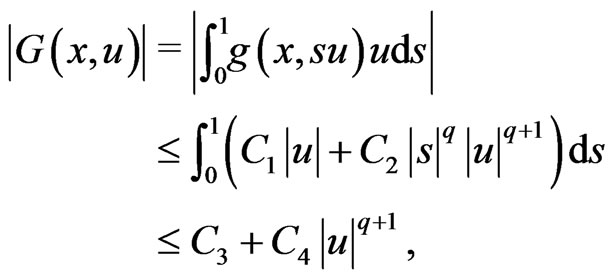
where .
.
Hence 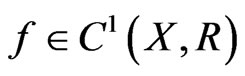 and maps bounded sets into bounded sets.
and maps bounded sets into bounded sets.
In fact,
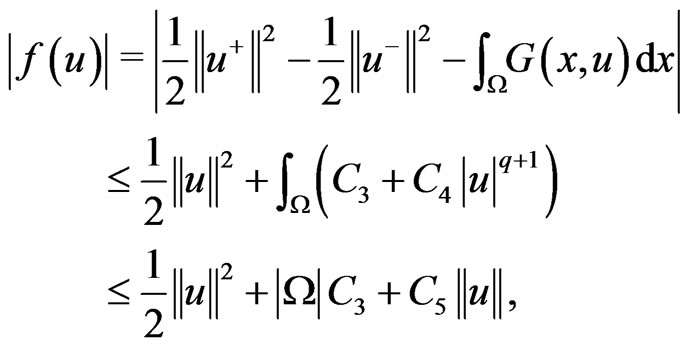
so (f3) holds.
2)  has a local linking at 0.
has a local linking at 0.
It follows from (g2) and (g3) that, for any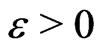 , there exists
, there exists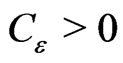 , such that
, such that
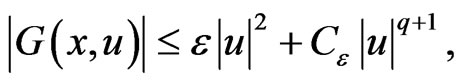 (4)
(4)
we obtain, on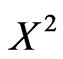 , for some
, for some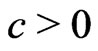 ,
,
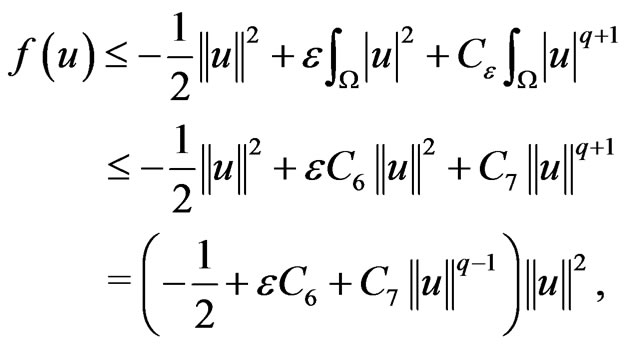
choosing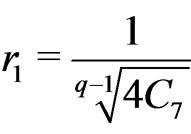 , then
, then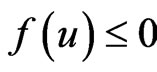 ,
,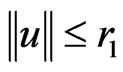
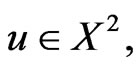 .
.
Decompose  into
into 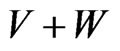 when
when  ,
,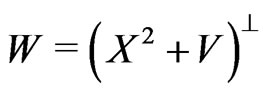 . Also set
. Also set 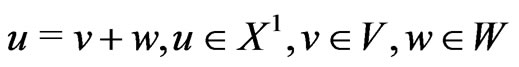 . Since
. Since 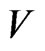 is a finitedimensional space, there exists
is a finitedimensional space, there exists , such that
, such that
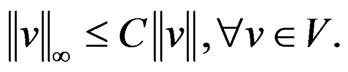 (5)
(5)
First we set 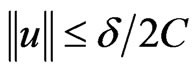 and
and
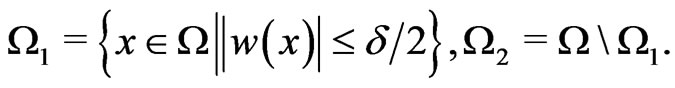
On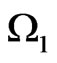 , we have, by (5)
, we have, by (5)

hence, by (2)
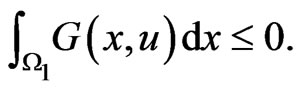
On , we have also by (5)
, we have also by (5)
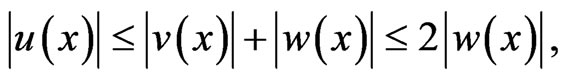
hence, by (4)
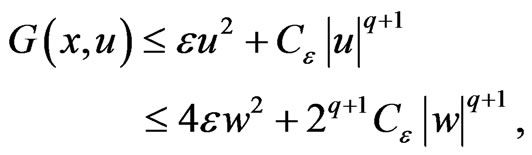
and for some 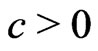
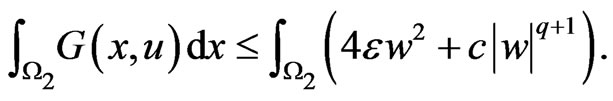
Therefore we deduce that
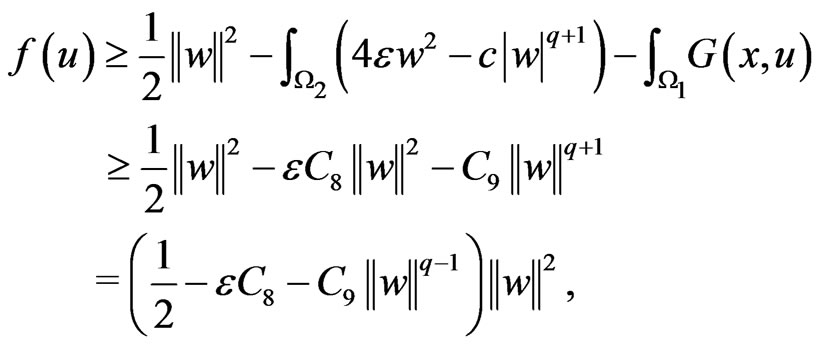
choosing , then
, then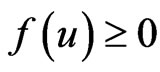 ,
, 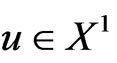 ,
, 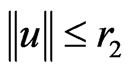 Let
Let , then (f1) holds.
, then (f1) holds.
3) 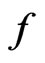 satisfies
satisfies 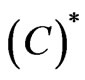 condition.
condition.
Consider a sequence  such that
such that  is admissible and
is admissible and
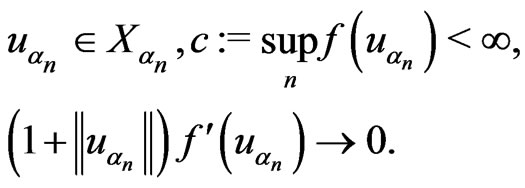
I)  is bounded.
is bounded.
For n large, from assumption (g3'), with , for some
, for some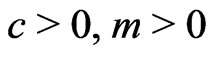 ,
,
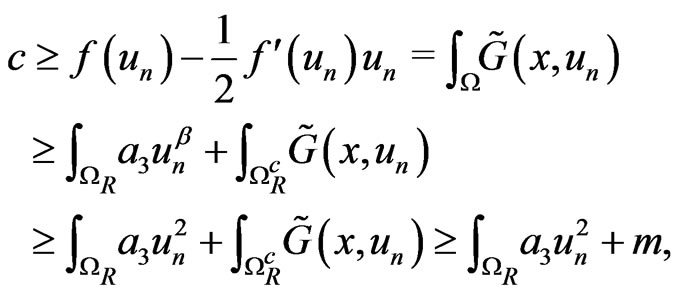
where 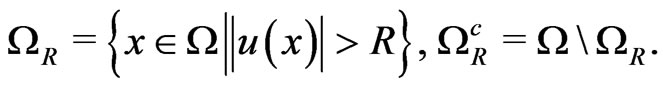
So
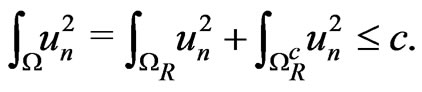 (6)
(6)
Arguing indirectly, assume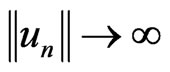 . Set
. Set 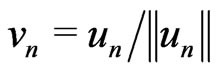 , Then
, Then 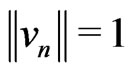 and
and 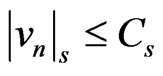 for all
for all 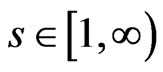 . In addition, using (6)
. In addition, using (6)

hence by Interpolation inequality for 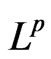 norms, for
norms, for 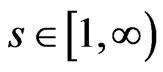
 (7)
(7)
where 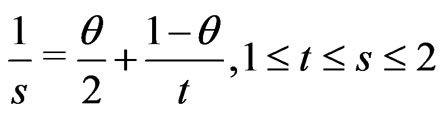 or
or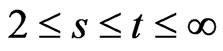 .
.
Since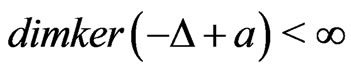 ,
,

so
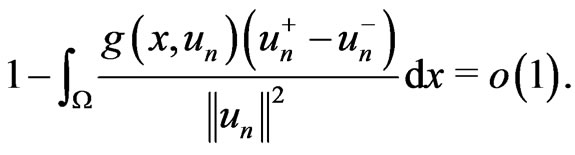
From (7) for some 
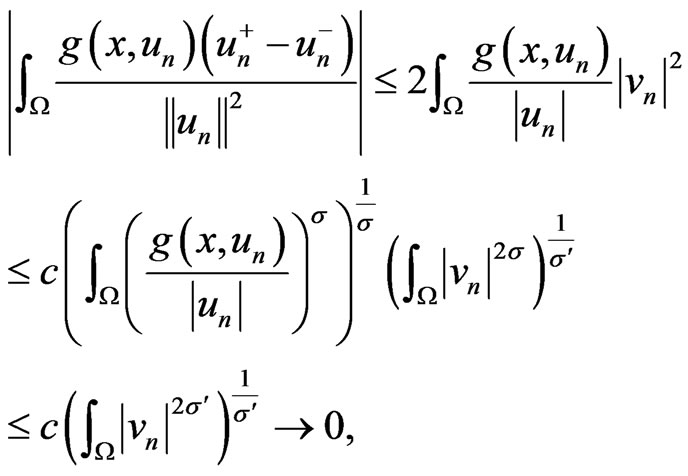
as , therefore,
, therefore,  , a contradiction. Hence
, a contradiction. Hence 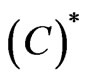 sequence is bounded.
sequence is bounded.
II) From (I) we see that 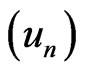 is bounded in
is bounded in , going if necessary to a subsequence, we can assume that
, going if necessary to a subsequence, we can assume that 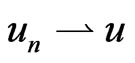 in
in . Since
. Since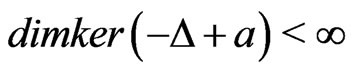 ,
, 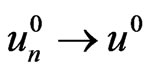 in
in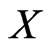 .
.
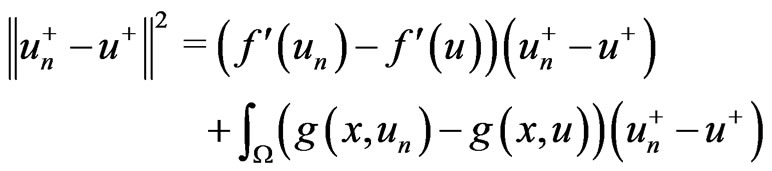
which implies that 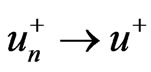 in
in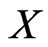 . Similarly,
. Similarly, 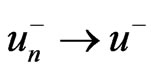 in
in . It follows then that
. It follows then that 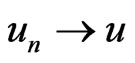 in
in  and
and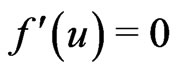 .
.
4) Finally, we claim that, for every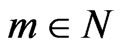 ,
,
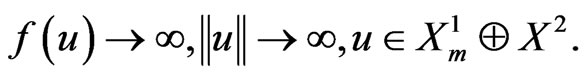
Indeed, by (g1) we have, there exists 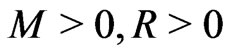 such that
such that
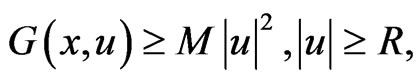
so on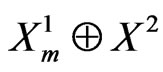 ,
,
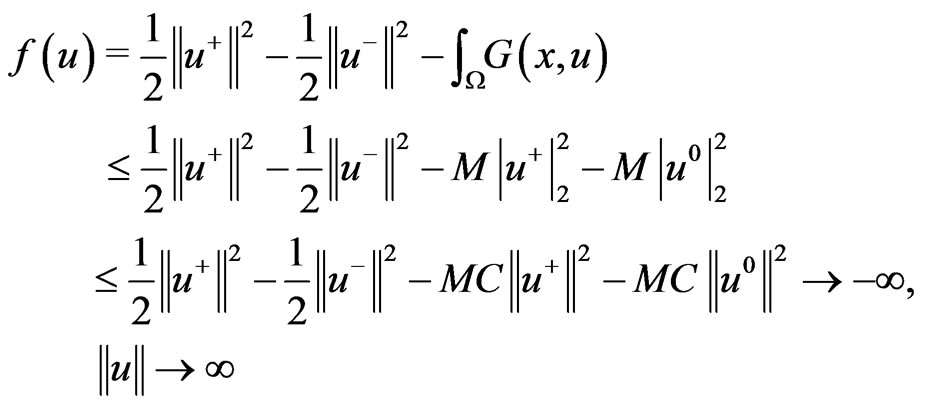
where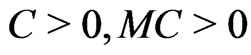 . □
. □
REFERENCES
- S. J. Li and M. Willem, “Applications of Local Linking to Critical Point Theory,” Journal of Mathematical Analysis and Applications, Vol. 189, No. 1, 1995, pp. 6-32. doi:10.1006/jmaa.1995.1002
- X.-L. Fan and Y.-Z. Zhao, “Linking and Multiplicity Results for the p-Laplacian on Unbounded Cylinders,” Journal of Mathematical Analysis and Applications, Vol. 260, No. 2, 2001, pp. 479-489. doi:10.1006/jmaa.2000.7468
- Q. S. Jiu and J. B. Su, “Existence and Multiplicity Results for Dirichlet Problems with p-Laplacian,” Journal of Mathematical Analysis and Applications, Vol. 281, No. 2, 2003, pp. 587-601. doi:10.1016/S0022-247X(03)00165-3
- P. H. Rabinowitz, “Periodic Solutions of Hamiltonian Systems,” Communications on Pure and Applied Mathematics, Vol. 31, No. 2, 1978, pp. 157-184. doi:10.1002/cpa.3160310203
- Q. Jiang and C. L. Tang, “Existence of a Nontrivial Solution for a Class of Superquadratic Elliptic Problems,” Nonlinear Analysis, Vol. 69, No. 2, 2008, pp. 523-529. doi:10.1016/j.na.2007.05.038
- S. X. Luan and A. M. Mao, “Periodic Solutions for a Class of Non-Autonomous Hamiltonian Systems,” Nonlinear Analysis, Vol. 61, No. 8, 2005, pp. 1413-1426. doi:10.1016/j.na.2005.01.108
NOTES
*Supported by NSFC(11101237).
#Corresponding author.

