World Journal of Mechanics
Vol.08 No.02(2018), Article ID:82519,13 pages
10.4236/wjm.2018.82004
A Study of the Elastodynamic Problem by Meshless Local Petrov-Galerkin Method Using the Laplace-Transform
Jaouad Eddaoudy, Touria Bouziane
Department of Physics, Faculty of Sciences, Moulay Ismail University, Meknes, Morocco
Copyright © 2018 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: December 19, 2017; Accepted: February 11, 2018; Published: February 14, 2018
ABSTRACT
The Meshless Local Petrov-Galerkin (MLPG) with Laplace transform is used for solving partial differential equation. Local weak form is developed using the weighted residual method locally from the dynamic partial differential equation and using the moving least square (MLS) method to construct shape function. This method is a more effective alternative than the finite element method for computer modelling and simulation of problems in engineering; however, the accuracy of the present method depends on a number of parameters deriving from local weak form and different subdomains. In this paper, the meshless local Petrov-Galerkin (MLPG) formulation is proposed for forced vibration analysis. First, the results are presented for different values of , and with regular distribution of nodes . After, the results are presented with fixed values of and for different time-step.
Keywords:
Meshless, MLPG, Weak Form, MLS, PDEs, Elastodynamic, Laplace Transform, Support Domain, Quadrature Domain, Regular Distribution

1. Introduction
Generality of physical or mechanical problems are modeled by partial differential equations (PDEs). Moreover, a high number of numerical methods and techniques have been developed for the approximation of solution of the PDEs in much research that focused mainly on the improvement of accuracy and efficiency of them. In recent years, attention has turned on the development of meshless methods, especially for the numerical solution of partial differential equations. The meshless local Petrov-Galerkin (MLPG) approach [1] - [14] has become very attractive, as a promising method for solving problems. This method based on a local weak form and Moving Least Squares (MLS) approximation [15] [16] [17] [18] . The main advantage of this method over the widely used finite element methods (FEM) is that it does not need any mesh, either for the interpolation of the solution variables or for the integration of the weak forms [19] [20] . The MLPG method and its variations have been applied for elastodynamic and elastostatic problems by several authors. For example, it is applied to free and forced vibration analysis for solids by Gu Y. T. et al. [21] they found that the parameter which decides the size of the sub-domain needs to be chosen carefully. Long S. Y. et al., have applied MLPG5 method used the Heaviside function as the test function for elastic dynamic problems [22] . They found a good agreement compared with the results obtained by (FEM). This method also applied by Ping Xia et al. in elastic dynamic analysis of moderately thick plate using meshless LRPIM [23] . They have used the Newmark method for solving the dynamic problem and have studied the effects of the size of the quadrature subdomain and the influence domain on the dynamic properties. They found if appropriate sizes are selected, good results and stability can be obtained. A meshfree-based local Galerkin method with condensation of degree of freedom for elastic dynamic analysis by De-An Hu et al. [24] , they have used the standard implicit Newmark’s time integration scheme for solving the global dynamic system equations obtained by assembling all local discrete equations. Recent results founded by Moussaoui and al concerning the effects of support domain for elastostatic problem by MLPG [25] .
The MLPG formulation is proposed in this paper to extend the MLPG method to dynamic analysis and for solving the problem of a thin elastodynamic homogeneous rectangular plate [26] . The Laplace transform [27] is applied to eliminate the time variable, then, the obtained equations by the local formulation becomes in function with coefficient of Laplace transform. The Stehfest inversion method is applied to obtain the time-dependent solutions [28] . The result presented for different values of and with regular distribution of nodes . After, the results are presented with fixed values of and for different time-step. We found large domains of , and time-step by using Laplace transform method. The integral equations have a very simple non-singular form. Moreover, both the contour and domain integrations can be easily carried out in rectangular sub-domains.
This paper is organized as follows: Section 2 introduces the least squares approximation (MLS) for combination of shape function. In Section 3, the Basic equations of elastodynamics and their Laplace transforms are proposed. In Section 4, the MLPG formula including the local weak form in Laplace-transformed domain are developed, using the weighted residual method locally from the dynamic partial differential equation. The numerical results and discussions for 2D problem example are given in Section 5. Finally, the paper ends with the conclusion.
2. Moving Least Square (MLS) Approximation
We Consider a sub-domain the neighbourhood of point , which is located within the problem domain . To approximate a function in , a finite set of monomial basis functions , is considered in the space coordinates in two-dimension is given by:
(1)
The approximation function of a field variable is defined in a subdomain by:
(2)
where is the monomial basis function of the spatial coordinates for two dimensional problem, and m is the number of the monomial basis functions. is a function of point and time and is a vector of coefficients given by:
(3)
The coefficient is obtained at any point by minimizing a weigh- ted discrete L2 norm
(4)
where n is the number of nodes in the support domain of for which the weight function , and is the nodal parameter of at .
The stationarity of with respect to gives:
(5)
which leads to the following linear relations:
(6)
where
is the vector that collects the nodal displacements for all nodes in the support domain:
(7)
is called the weighted moment matrix defined by:
(8)
and the matrix B is defined by:
(9)
Solving from Equation (6) as:
(10)
and substituting the above Equation (10) back into Equation (2) we obtain:
(11)
where is the matrix of MLS shape functions corresponding n nodes in the support domain of the point and can be written as:
(12)
The shape function for the ith node is defined by:
(13)
The following quartic spline function is used, it has the following form of
(14)
In which is the distance from node to point , and is the size of the influence domain for the weight function.
3. Basic Equations of Elastodynamics
The governing equations for a linear two-dimensional elastodynamic problem on a domain Ω bounded by a boundary Γ are:
(15)
(16)
(17)
where the mass density, c is the damping coefficient, is the acceleration, the velocity, the stress tensor, the body force tensor, and denotes
The initial and boundary conditions are given as follows:
(18)
(19)
(20)
(21)
where and are the prescribed displacement and traction on the boundary and respectively, and denote the initial displacement and initial velocity, is the unit outward normal to the boundary . and are complementary subsets of .
The Laplace-transform [27] of a function is defined by:
(22)
(23)
(24)
Then the Laplace-transform of the basic Equation (15) gives the general expression of the partial differential equation:
(25)
where
(26)
4. The MLPG Weak Formulation in Laplace-Transformed Domain
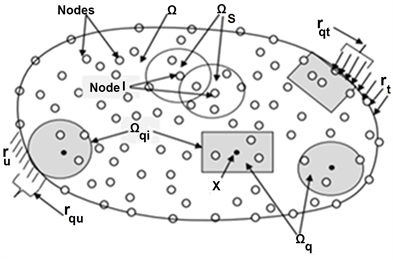
The MLPG (meshless local Petrov-Galerkin) method constructs the weak form over local subdomain such as , which is a small region taken for each node inside the global domain. The local subdomains overlap, and cover the whole global domain . In the present paper, the local subdomains are taken to be of a quadrature shape. The local weak form [20] [21] of the governing Equation (25) can be written as:
(27)
where is a test function:
by using
(28)
and applying the Gauss divergence theorem we can write:
(29)
where
(30)
is the boundary of the local subdomain, which is consisted of three parts, i.e.
(See Figure 1)
is the local boundary that is totally inside the global domain,
is the part of the local boundary, which lies on the global boundary with prescribed tractions, i.e.
is the part of the local boundary that lies on the global boundary with prescribed displacements, i.e.
and considering:
(31)
Figure 1. The support domain ΩS and integration domain Ωq for node I.
The local weak form in Equation (29) is leading to the following local integral equation:
(32)
The strains can be obtained using the approximated displacements:
(33)
Considering Equation (11) with Laplace transform:
(34)
(35)
The constitutive equation gives the relationship between the stress and the strain:
(36)
The traction vectors at a boundary point are approximated by numbers of nodal values as:
(37)
where the matrix related to the normal vector of by:
(38)
The matrix represented by the gradients of the shape functions as:
(39)
The stress-strain matrix D for plane stress is defined by:
(40)
In which E is the Young’s modulus and is the Poisson’s ratio.
Obeying the boundary conditions at those nodal points on the global boundary, where displacements are prescribed, and making use of the approximation formulae Equation (11), we obtains the discretized form of the displacement boundary conditions:
(41)
Substituting equations. (36) and (37) into Equation (32) we obtain the discretized Local integral equations:
(42)
where is a matrix of weight functions given by:
(43)
is a matrix that collects the derivatives of the weight:
(44)
The cubic spline functions are used as the test functions for the local weak form:
(45)
where
In which is the distance from node to point , and is the size of the influence domain for the weight function.
Collecting the discretized local integral equations together with the discretized boundary conditions for displacements, we get the complete system of algebraic equations for computation of nodal displacements, which are the Laplace transforms of fictitious parameters .
The time dependent values of the transformed variables can be obtained by an inverse Laplace transform. There are many inversion methods available for the Laplace transformation. In the present analysis, the Stehfest algorithm [28] is used. If
is the Laplace-transform of
, an approximate value
of
for a specific time
(46)
The selected number N = 10 with a single precision arithmetic is optimal to receive accurate results. It means that for each time t, it is needed to solve N boundary value problems for the corresponding Laplace parameters force with . If M denotes the number of the time instants in which we are interested to know g(t), the number of the Laplace transform solutions is then M × N.
5. Numerical Results and Discussions
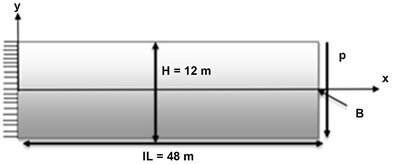
In this section, numerical results will be presented to illustrate the implementation and effectiveness of the proposed method. We present a numerical study for elastodynamic 2-D problem of a rectangular homogeneous isotropic plate [26] by using MLPG method, subjected to a dynamic force at the right end (Figure 2). A plane stress problem is considered, and a unit thickness is used. The dimensions of plate are length and height . The external excitation force , where (simple harmonic load with ) is a function of time, the damping coefficient is fixed for all numerical computation. A total number uniformly distributed nodes is used, as shown in Figure 3, to represent the problem domain.
The dimension of the quadrature domain is set to , where is the size of the quadrature domain, is a distance to the first nearest neighbouring point from node i. The dimension of the influence domain is set to , where is the size of the support domain.
The isotropic rectangular plate analyzed with the following material properties: in Steel. Some important parameters on the performance of the method have been investigated.
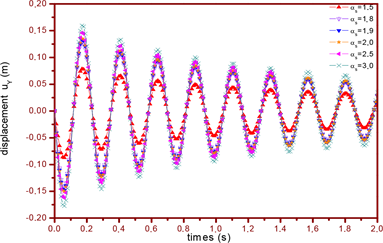
Figure 4 displays the variations of displacements as a function of time at point B under the harmonic load for different values of size of support domain , where the time step is . It can be seen
Figure 2. Rectangular homogeneous isotropic plate subjected to a dynamic force at the right end of the plate.
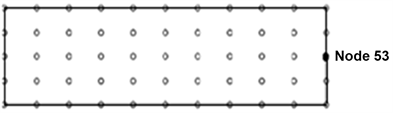
Figure 3.Configuration and nodal arrangement for the plate.
Figure 4. Displacements uy at the middle point B at the free end of the plate excited by the time-step load for different values of where and .
from this figure that the size of support domain influences on the results if , and has a small effect on the results if ). When , the results obtained by the present method is very good compared with the other authors [21] that have used the Newmark method. In the following analysis, is employed.
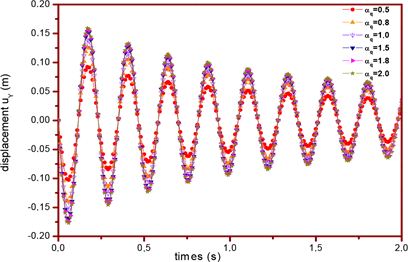
The time variation of displacements are given in Figure 5 with different values of size of the quadrature domain , where . It is found that the size of the quadrature domain influences seriously the results if and has a small effect on the results if .
Figure 5. The time variation of displacements uy for different values of where and .
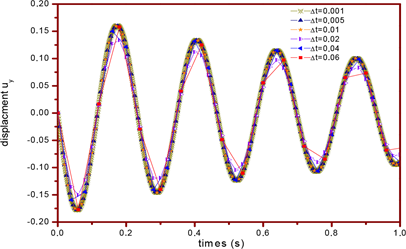
Figure 6. The time variation of displacements in the y direction at the point B with different time steps using the fixed values .
However, if the size of the quadrature domain is too large, the result obtained for displacements by MLPG is great. We found good results with comparing with the results obtained by Long S. Y et al. [22] , they have used .
Many time steps are used in computation to check the stability of the presented MLPG formulation. The displacement variations as a function of time and results for different time steps are plotted in Figure 6. It can be found that when the time step is less than 0.02 s, perfect results have been obtained using the Laplace transform comparing with the results obtained by other authors [23] [24] that have used the Newmark method. It also can be found that when a time step is larger than 0.02 s, the results are not convergent and not accurate.
6. Conclusion
The present method MLPG that uses the cubic spline test function is used to analyze elastodynamic problem. The equation formulation based on MLPG method in Laplace transform and time domain with MLS approximation has been successfully implemented to solve elastodynamic problems in isotropic solids, subjected to a dynamic force at the right end of the plate. We found that the amplitude of the vibration decreases with time because the effects of damping and the harmonic load, the response should converge to the static deformation. We found that when the time step is less than 0.02 s, perfect results have been obtained by using the Laplace transform and when a time step is larger than 0.02 s the results are not accurate. We found that the size of the quadrature domain has a small effect on the results if , and the size of the support domain influences on the results if . The sizing parameters and , which decides the size of the subdomain needs to be chosen carefully, especially, in the dynamic analysis.
Cite this paper
Eddaoudy, J. and Bouziane, T. (2018) A Study of the Elastodynamic Problem by Meshless Local Petrov-Galerkin Method Using the Laplace- Transform. World Journal of Mechanics, 8, 46-58. https://doi.org/10.4236/wjm.2018.82004
References
- 1. Atluri, S.N. and Zhu, T.L. (1998) A New Meshless Local Petrov-Galerkin (MLPG) Approach in Computational Mechanics. Computational Mechanics, 22, 117-127. https://doi.org/10.1007/s004660050346
- 2. Atluri, S.N. and Zhu, T.L. (2000) The Meshless Local Petrov-Galerkin (MLPG) Approach for Solving Problems in Elasto-Statics. Computational Mechanics, 25, 169-179. https://doi.org/10.1007/s004660050467
- 3. Sladek, J., Sladek, V., Wen, P.H. and Aliabadi, M.H. (2006) Meshless Local Petrov-Galerkin (MLPG) Method for Shear Deformable Shells Analysis. CMES: Computer Modeling in Engn. & Sciences, 13, 103-118.
- 4. Sladek, J., Sladek, V., Zhang, C. and Solek, P. (2007) Application of the MLPG to Thermopiezoelectricity. CMES: Computer Modeling in Engn. & Sciences, 22, 217-233.
- 5. Mirzaei, D. and Dehghan, M. (2010) Meshless Local Petrov-Galerkin (MLPG) Approximation to the Two Dimensional Sine-Gordon Equation. Journal of Computational and Applied Mathematics, 233, 2737-2754. https://doi.org/10.1016/j.cam.2009.11.022
- 6. Sladek, J., Stanak, P., Han, Z.D., Sladek, V. and Atluri, S.N. (2013) Applications of the MLPG Method in Engineering & Sciences: A Review. CMES, Computer Modeling in Engn. & Sciences, 92, 423-475.
- 7. Zhang, T., Dong, L.T., Alotaibi, A. and Satya, A.N. (2013) Application of the MLPG Mixed Collocation Method for Solving Inverse Problems of Linear Isotropic/Anisotropic Elasticity with Simply/Multiply-Connected Domains. CMES, Computer Modeling in Engn. & Sciences, 94, 1-28.
- 8. Stanak, P., Sladek, V., Sladek, J., Krahuleca, S. and Sator, L. (2013) Application of Patch Test in Meshless Analysis of Continuously Non-Homogeneous Piezoelectric Circular Plate. Applied and Computational Mechanics, 7, 65-76.
- 9. Atluri, S.N. and Shen, S.P. (2002) The Meshless Local Petrov-Galerkin (MLPG) Method: A Simple & Less-Costly Alternative to the Finite Element and Boundary Element Methods. CMES, 3, 11-51.
- 10. Sladek, J., Sladek, V. and Keer, R.V. (2003) Meshless Local Boundary Integral Equation Method for 2D Elastodynamic Problems. International Journal for Numerical Methods in Engineering, 57, 235-249. https://doi.org/10.1002/nme.675
- 11. Qian, L.-F. and Ching, H.-K. (2004) Static and Dynamic Analysis of 2-d Functionally Graded Elasticity by using Meshless Local Petrov Galerkin Method. Journal of the Chinese Institute of Engineers, 27, 491-503. https://doi.org/10.1080/02533839.2004.9670899
- 12. Han, Z.D. and Atluri, S.N. (2004) Meshless Local Petrov-Galerkin (MLPG) Approaches for Solving 3D Problems in Elasto-Statics. Computer Modeling in Engineering & Sciences, 6, 168-188.
- 13. Han, Z.D. and Atluri, S.N. (2004) A Meshless Local Petrov-Galerkin (MLPG) Approach for 3-Dimensional Elastodynamics. Computers Materials & Continua, 1, 129-140.
- 14. Atluri, S.N., Han, Z.D. and Shen, S. (2003) Meshless Local Petrov-Galerkin (MLPG) Approaches for Solving the Weakly-Singular Traction & Displacement Boundary Integral Equations, CMES, 4, 507-517.
- 15. Lancaster, P. and Salkauskas, K. (1981) Surfaces Generated by Moving Least Squares Methods. Mathematics of Computation 37, 141-158. https://doi.org/10.1090/S0025-5718-1981-0616367-1
- 16. Li, D., Wei, A., Luo, K. and Fan, J. (2015) An Improved Moving-Least-Squares Reconstruction for Immersed Boundary Method, International Journal for Numerical Methods in Engineering, 104, 789-804. https://doi.org/10.1002/nme.4949
- 17. Shivanian, E. (2016) Local Integration of Population Dynamics via Moving Least Squares Approximation, Engineering with Computers, 32, 331-342. https://doi.org/10.1007/s00366-015-0424-z
- 18. Belytschko, T., Krongauz, Y., Organ, D., Fleming, M. and Krysl, P. (1996) Meshless Methods: An Overview and Recent Developments. Computer Methods in Applied Mechanics and Engineering, 139, 3-47. https://doi.org/10.1016/S0045-7825(96)01078-X
- 19. Pandey, S.S., Kasundra, P.K. and Daxini, S.D. (2013) Introduction of Meshfree Methods and Implementation of Element Free Galerkin (EFG) Method to Beam Problem. International Journal on Theoretical and Applied Research in Mechanical Engineering, 2, 2319-3182.
- 20. Atluri, S.N., Cho, J.Y. and Kim, H.G. (1999) Analysis of Thin Beams using the Meshless Local Petrov-Galerkin Method with Generalized Moving Least Squares Interpolations. Computational Mechanics, 24, 334-347. https://doi.org/10.1007/s004660050456
- 21. Gu, Y.T. and Liu, G.R. (2001) A Meshless Local Petrov-Galerkin (MLPG) Method for Free and Forced Vibration Analyses for Solids. Computational Mechanics, 27, 188-198. https://doi.org/10.1007/s004660100237
- 22. Long, S.Y., Liu, K.Y. and Hu, D.A. (2006) A New Meshless Method Based on MLPG for Elastic Dynamic Problems. Engineering Analysis with Boundary Elements, 30, 43-48. https://doi.org/10.1016/j.enganabound.2005.09.001
- 23. Xia, P., Long, S. and Cui, H. (2009) Elastic Dynamic Analysis of Moderately Thick Plate using Meshless LRPIM. Acta Mechanica Solida Sinica, 22, 116-124. https://doi.org/10.1016/S0894-9166(09)60096-3
- 24. Hu, D., Yi, G.W., Li, Y., Han, X. and Gu, Y.T. (2014) A Meshfree-Based Local Galerkin Method with Condensation of Degree of Freedom for Elastic Dynamic Analysis. Acta Mechanica Sinica, 30, 92-99. https://doi.org/10.1007/s10409-013-0090-6
- 25. Moussaoui, A. and Bouziane, T. (2013) Comparative Study of the Effect of the Parameters of Sizing Data on Results by the Meshless Methods (MLPG). World Journal of Mechanics, 3, 82-87. https://doi.org/10.4236/wjm.2013.31006
- 26. Timoshenk, S. (1959) Theory of Plates and Shells. McGraw-Hill, New York, 2.
- 27. Davies, B. and Martin, B. (1979) Numerical Inversion of the Laplace Transform: A Survey and Comparison of Methods. Journal of Computational Physics, 33, 1-32. https://doi.org/10.1016/0021-9991(79)90025-1
- 28. Stehfest (1970) Algorithm 368: Numerical Inversion of Laplace Transform. Communications of the ACM, 13, 47-49.