World Journal of Mechanics
Vol.06 No.09(2016), Article ID:71056,17 pages
10.4236/wjm.2016.69024
Drag on a Cylinder with an Apple-Shaped Cross Section
Hirono Matsumoto1, Yoshihiro Kubota2, Masayuki Ohishi3, Osamu Mochizuki4
1Graduate School of Biomedical Engineering, Toyo University, Saitama, Japan
2Faculty of Science and Engineering, Toyo University, Saitama, Japan
3Daikirika Kogyo Inc., Saitama, Japan
4Department of Biomedical Engineering, Toyo University, Saitama, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 25, 2016; Accepted: September 27, 2016; Published: September 30, 2016
ABSTRACT
The drag on a cylinder with an apple-shaped cross section was studied numerically in this paper. This cross section is adopted because the drag on an apple is known to be lower than that of a sphere. Since the hollows of an apple seem to be points of drag reduction, two-dimensional numerical simulations of cylinders with hollows of several shapes are carried out at a Reynolds number of 6.7 × 104 by using the vortex method to check their effects. The cylinder with hollows like those of a real apple attained a 13% reduction in drag compared with a circular cylinder. Other geometrical hollow-shapes, namely, V-shaped and U-shaped grooves, also reduced drag from the circular model, but these effects were less pronounced than those of the apple-shaped cross section. It was concluded that an apple-like hollows were effective for drag reduction of a cylinder as well as a sphere.
Keywords:
Drag Reduction, Apple, Cylinder, Vortex Method, k-ε Model, Flow Visualization

1. Introduction
Reducing the drag on a blunt body relates to the control of the flow separation. The location at which the boundary layer along the surface of a body separates depends on the state of the boundary-layer flow, whether laminar, transition, or turbulent. If the boundary layer is laminar, the separation point is 89 degrees measured from the front stagnation point of a circular cylinder. If it is turbulent, the separation point is 130 degrees. Since the drag is related to the pressure distribution along the surface of the blunt body, the large width of the wake between the separation shear layers increases the drag. Thus, when the laminar boundary layer on a circular cylinder separates, the drag must be larger than that in the case of a turbulent boundary layer. For passive drag reduction, the laminar boundary can be promoted to a turbulent one by placing a small rod in front of the circular cylinder [1] ; placing small rods [2] , tripping wires [3] , bumps [4] , lateral [5] or longitudinal V-grooves [6] [7] or longitudinal U-grooves on the cylinder’s surface [8] - [10] ; adding longitudinal grooves like those of a cactus [11] [12] ; increasing surface roughness [13] or porousness [14] ; or adding patterns [15] like the dimples of a golf ball.
The way to avoid a fall disaster of an apple due to strong wind of typhoon has been researched by the authors. When the drag force of an apple was measured, its drag coefficient was found to be 23% smaller than that of a sphere at a Reynolds number of order 104 [16] . If this is true, the apple’s shape offers us a clue for reducing the drag on a blunt body. The shape of an apple differs from that of a sphere due to the presence of hollows located in the apple’s top and bottom. For understanding the effect of these hollows upon drag reduction, the flow around an apple was visualized experimentally by using a hydrogen bubble technique in a water tank and was conducted a three-di- mensional numerical simulation by solving the Navier-Stokes equations. The hollows might be a cause of a separation delay. The drag of a cylinder with a cross section similar to that of an apple was obtained by a vortex method using a two-dimensional numerical simulation [17] .
In this paper, the drags on apple-shaped cylinders with different shaped hollows were compared with those of the cylinders with V- and U-shaped grooves. The apple-shaped cylindrical cross section showed favorable reduction of drag, similar to that of a cross section shaped like a cactus. This means that the cross sections of natural things may induce low drag when exposed to wind. The influence of the flow through differently shaped hollows on the separation is discussed in this paper.
2. Experimental Setup
The open water channel used for the flow-visualization experiment is shown in Figure 1; the channel has a dimension of 0.18 m in width, 0.22 m in height, and 1.0 m length. The free stream velocity was 0.18 m/s.The tested model resembling a real Jonathan apple was set in water. This model was accurately made using silicon (Shin-Etu silicon KE-12) to realize the profile and hollows of a real apple. Based on measurements of a real apple specimen, the model had a diameter of 76 mm and a height 75 mm (i.e., it was nearly spherical). The Reynolds number based on the free stream velocity and the apple’s diameter was 1.4 × 104 for visualization experiments. The blockage effect of the apple in the test section was 11%. For investigating the effect of the hollow, an apple model whose hollow was covered was prepared, too.
The flow around the apple model was visualized using the hydrogen bubble technique. Hydrogen bubbles were generated by a tungsten wire connected to the negative electrode of a DC-voltage power supply. The diameter of the wire was 0.05 mm and was placed 70 mm upstream of the model. A copper plate connected to a positive electrode
Figure 1. Experimental setup. Apple model in the test section of an open water channel.
was placed downstream in the water tank. A light sheet illuminated a vertical plane of the flow around the apple. A digital camera was used to record the flow patterns presented by hydrogen bubbles over 2 minutes. The images were superimposed to enhance the contrast and to obtain the time-averaged patterns. The half width of the wake was measured from the superimposed photos using Image J, an image-processing software developed by the National Institutes of Health.
3. Numerical Simulation
3.1. Three-Dimensional Simulation Using FLUENT
In the previous experiment done by the authors [16] , the drag coefficient of an apple was found to be 0.36 and that of a sphere to be 0.49 at a Reynolds number of order of 104. This suggests that the shape in nature has a useful ability that can be applied to engineering fields. Physical quantities of the flow passing an apple and the forces acting on the apple are not obtained from the flow visualization in a water tank; therefore, a three-dimensional numerical simulation of the flow around an apple model with and without hollows was carried out, which will be shown later in Figure 2. For convenience, the Navier-Stokes equations were solved at Reynolds number (Re) = 6.7 × 104 using the well-known ANSYS FLUENT commercial software. A standard k - ε model was used for solving the flow around the apple models. The boundary conditions were a no-slip condition at the surface of the apple model, a constant free stream velocity at the inlet, and a pressure outlet at which the gauge pressure was set to zero. The resulting output was the pattern of the streamlines for comparison to the experimental results, and the wall-shear stress on the surface of the apple model for seeking the separation lines.
3.2. Two-Dimensional Simulation Using the Vortex Method
A two-dimensional numerical simulation based on the vortex method was used for
Figure 2. Longitudinal cross section of an apple consisting of two overlapping ellipses whose centers are located at ±x0, matching with the apple section.
solving the flow around a circular cylinder with hollows (which are called grooves in the case of a cylinder) at high Reynolds number. The vortex method is free from mesh, making it relatively easy to present the flow near the groove, even if the groove is a complicated geometrical shape [18] . The advantages of the vortex method are as follows: it 1) is free from mesh, 2) is applicable for expressing flows with a wide range of Reynolds numbers, including laminar and turbulent flows, and 3) can obtain the precise forces acting on a body in a manner based on momentum theory. It is suitable for testing the effects of several cross-section shapes upon fluid dynamic forces.
The governing equations of flow in the vortex method are the vorticity-transport equation, which is obtained from the Navier-Stokes equations under a rotation operation; the continuity equation; and the Poisson equation. The vorticity, 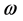 , is defined as
, is defined as
 (1)
(1)
Here, 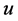 shows a velocity vector. The velocity vector field can be induced uniquely from the vorticity field according to the Biot-Savart law presented in Equation (2):
shows a velocity vector. The velocity vector field can be induced uniquely from the vorticity field according to the Biot-Savart law presented in Equation (2):
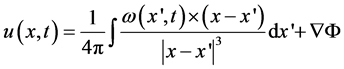 (2)
(2)
The first term in Equation (2) is the Biot-Savart law and the second term is a correction to the velocity caused by boundary surfaces in the flow. The vorticity field is formed by vortex blobs that represent a body in a flow, boundary layers on the body, and shear flows shedding from the body. The vortex blobs that represent both boundary layers and shear flows are produced at each time step, and their vorticity decays in time according to the core-spreading method [17] . The drag and lift forces are calculated by integrating the pressure and shear stress acting on the surface of the body. The forces acting on the body are obtained by solving the Poisson equation about the pressure expressed by Bernoulli’s function. The commercial software (VFS VOs-2D, College Master Hans Co.) based on the above principle was used for this simulation.
3.3. Calculation Model of an Apple
A half-part of a longitudinal section of an apple is presented by an ellipse of b/a = 1.7, as shown in Figure 2. The two-dimensional model of an apple for the numerical simulations is a cylinder with an apple-shaped cross section represented by two ellipses. For simplicity, this cylinder is called “an apple-shaped cylinder”. The three-dimensional model is a solid that can be obtained by rotating the ellipse around the y-axis.
The cross section of the apple-shaped cylinder consisted of two overlapped ellipses characterized by both the x0value of the center of the ellipse and the aspect ratio b/a = 1.7. The hollows of the apple-shaped cylinder formed at the north pole at 90 degrees latitude and south pole of −90 degrees latitude. The representative length in the x-direction, 2(x0 + a), was equal to 1 and that in y-direction, 2b, was also equal to 1. The shape that has x0 = ±0.2 and b/a = 1.7 was the basic form of an apple model and was named “apple020” in our numerical simulations. Several variations of the form were tested for comparison with the basic form. A series of variations was designed by obeying the following rule: keep the length in x-direction 2(x0 + a) = 1 and the length in y-direction 2b = 1, and change x0 and b/a to change the overlap of the two ellipses. Tested forms are shown in Figure 3. The center position, x0, in the positive x-direction
becomes the model name; for instance, the model shown in Figure 3(a) with one ellipse centered at x0 = 0.25 is called apple025. Apple000 is a circular cylinder, so it is named “circle”. The other forms tested are “V-shaped”, “U-shaped”, hollow, and one with a “flat top” attached to the basic form are shown in Figure 4. For comparison, a shape like that of “flat top” turned 90 degrees was also tested, and it was named “flat front shape”.
4. Results
4.1. Experimental Results
The flow around an apple model is shown in Figure 5. The model in Figure 5(a) is identical in shape to a real one. The model in Figure 5(b) has the same general outline, but its hollows are completely filled. The distance between the upper and lower shear layers at the rear rim of the model in Figure 5(a) is 11% smaller than that of the model in Figure 5(b). This means that since the hollows retard separation, they cause the wake to contract, thereby reducing drag. The region in which large-scale vortex-formation occurs seems to be longer for the realistic model than for the model without hollows; this shows that the roll-up vortices consisting of the separated shear layer must be weak in the wake of the apple. Therefore, the magnitude of the lift force’s fluctuation may be small.
Figure 3. Various forms of the apple model. (a) apple025: x0 = 0.25, b/a = 2.0; (b) apple020: x0 = 0.20, b/a = 1.7; (c) apple015: x0 = 0.15, b/a = 1.4; (d) apple010: x0 = 0.10, b/a = 1.3; (e) apple005: x0 = 0.05, b/a = 1.1; (f) apple000 (circle): x0 = 0.00, b/a = 1.0.
Figure 4. Additive model with geometric shapes. (g) V-shaped hollow; (h) U-shaped hollow; (i) flat top without hollow attached to the basic form.
4.2. Results of Numerical Simulation Using the FLUENT
The wake presented by streamlines around the apple in Figure 6(a) seems to be smaller than that for the model without hollows in Figure 6(b). This is similar to the visualization results shown in Figure 5, indicating that the drag is independent of the apple’s material because a no-slip condition is enforced on the apple’s surface. Therefore, the hollows influence the separation characteristics of the blunt body, and may reduce drag on the body. For investigating the relationship between the shape of the hollow and drag, the drag on cylinders with different hollow shapes will be presented in the next section.
4.3. Results of Numerical Simulation Using the Vortex Method
The flow patterns depicted based on the vortices shed from the apple-shaped cylinder with grooves are shown in Figure 7. The free stream velocity is 10 m/s, and the


Figure 5. Hydrogen-bubble flow visualization around an apple model in a water tank. The Reynolds number is 1.4 × 104. Different apple models are used: (a) model with the same shape as a real apple; (b) model with the same outline as that of (a) but with its hollows completely filled. The width of the wake of the apple is smaller than that of the apple without hollows.
representative length is 0.1 m in height, like that of a real apple. Thus, the Reynolds number based on the kinematic viscosity of air, ν = 1.5 × 10−5, is 6.7 × 104. Each of the figures shows a flow field obtained at around 5 seconds in a real time from beginning of the calculation. Yellow dots present vortex elements of positive vorticity generated from the surface of the cylinder, whereas blue dots present those with negative vorticity.
These elements form large-scale vortex structures behind the cylinder, whose rows are known as a Kármán vortex street. The large vortex structure consisting of yellow dots has a positive circulation Γ, whereas that consisting of blue dots has a negative


Figure 6. Stream lines around (a) the apple model and (b) the model without hollows. The wake patterns seem to be affected by hollows.
Figure 7. Flow patterns presented by vortices shed from the apple-shaped cylinder with different groove sizes. (a) apple025, (b) apple020, (c) apple015, (d) apple010, (e) apple005, and (f) apple000 (circle). Vortical structures in hollows affect on the flow structures in the wake.
circulation Γ. If there is a large vortex structure in which yellow and blue dots are mixed in near-equal proportions, the strength of the vortex structure is weak due to cancellation. The intermediate region at which yellow and blue dots exist side by side near the wall shows a separated shear layer. The flow pattern in the case of the cylinder with deep grooves seen in Figure 3(a) is shown in Figure 7(a). In this manner, the symbols of figures in Figure 2 and Figure 3 correspond to those in Figure 7 and Figure 8, respectively. The flow patterns seem to be almost the same, even for grooves of different shapes. However, the strength of the large-scale vortices grows weaker with increasing the groove depth; that in the case of a small groove is as strong as that in the case of the circular cylinder, according to the degree of concentration of yellow and blue dots.
Figure 8. Flow patterns of vortices shed from additive models with various geometric shapes: (g) V-shaped grooves, (h) U-shaped grooves, (i) apple020flat-top: flattop without a groove attached to the basic form, and (j) apple020flat-front; flat front without a groove attached to the basic form. The shape of groove has an influence on the vortical structure in hollows.
Figure 8 shows flow patterns of vortices shed from additive models with geometric shapes such as (g) V-shaped and (h) U-shaped grooves, and the models (i) apple020 flat-top and (j) apple020 flat-front without grooves. The geometric groove has sharp corners and edges; therefore, the separation points are fixed there and vortices within the hollow seem to be bounded. Thus, the bounded vortices seem to be characterized by the size of geometric groove, namely, its height and width. The groove of the apple- shaped cylinder has no such sharp edges facing the flow except for the cusp of the valley. This causes intuitive differences as seen in Figure 7 and Figure 8. It is a visible feature that pairings of vortices generated from both the up and down sides occur frequently compared with the flow around the apple-shaped cylinder, as seen at right in Figure 8.
The Strouhal numbers, St, measured from the fluctuation of the lift force for each case are shown in Figure 9. The St of a circular cylinder at Re = 6.7 × 104 is given as 0.19 - 0.21 experimentally. The circular cylinder in this calculation shows St = 0.18. The St value of the apple-shaped cylinders, including the cylinder with a U-shaped groove, fall in the range from 0.18 to 0.20; therefore, the influence of the groove upon the characteristics of vortex shedding is small. In contrast, the cylinder with a V-shaped groove shows St = 0.15, which is smaller than the others, and apple020 flat-front shows
Figure 9. Strouhal number of vortex shedding from the cylinder.
St = 0.29, which is higher than the others. This is a general feature [19] of blunt bodies that show low drag.
The experimentally measured drag coefficient of a circular cylinder was CD = 1.1 at Re = 6.7 × 104, but the result obtained by this two-dimensional vortex method was CD = 1.5. This larger value of the drag coefficient is due to the two-dimensionality of the numerical simulation. The change rate, R, of each value of drag compared with that of the circular cylinder is calculated as follows and is shown in Figure 10:
 (%). (3)
(%). (3)
Here, CD:circle is the drag coefficient of the circular cylinder, CD:circle = 1.5. The drag coefficients of the apple-shaped cylinders other than apple005 and apple010 were smaller than that of the circular cylinder. The apple025 model achieved a 50% reduction of drag coefficient compared with that of the circular cylinder. The apple020 model, which was very similar to a real apple, achieved a 13% reduction. The apple015 model achieved a 5% reduction. In contrast, the models apple010 and apple005 actually increased drag above that for a circular cylinder. The apple020 flat-top model, whose groove was covered by a flat plate, showed a 5.6% reduction in drag. This means that not only existence of a groove but also the shape of the apple was effective for reducing drag. The U-shaped and V-shaped grooves also reduced drag to the same degree as the flat top. This means that the shape most similar to the natural shape of an apple reduced drag more effectively than did artificial shapes such as those with V- and U-shaped grooves. The apple020flat-front showed a 39% reduction because of its streamlined body. The reduction for apple025 exceeded that for apple020flat-front. A detailed comparison between them will be discussed later.
The signals of the drag and lift coefficients over 550 ms obtained by the flow around apple020 are shown in Figure 11. The drag includes high-frequency fluctuations. The lift oscillated with a large amplitude and St = 0.17. A comparison of standard deviations,
Figure 10. Drag coefficients for various groove shapes.
Figure 11. Change in drag and lift forces of apple020. Red and blue lines show non-dimensional drag and lift, respectively.
STD, of the lifts obtained by each cylinder is shown in Figure 12. Low (high)-drag cylinder stended to have low (high) STDs. The apple010 model showed the largest STD because it showed the largest drag. The apple025 model showed the lowest STD because it had the lowest drag.
5. Discussion
It is a motivation of this study that the drag coefficient of an apple is lower than that of a sphere from our previous experiments. For checking the reason for this observation, flow-visualization experiments and numerical simulations with a three-dimensional apple model were carried out. Those results showed that the wake of the apple is smaller than that of the sphere. This means that the position of dynamic separation moves to the rear side of the apple. The effects of the shape of an apple’s hollows on drag reduction were tested using a two-dimensional numerical simulation known as the vortex method. The flows around apple-shaped cylinders with several different grooves were calculated and compared.
It is interesting that the degree of reduction of drag depends on the shape of the groove. Figure 13 shows a close-up view of the flow patterns in a hollow. The area in which many dots are concentrated presents a strong eddy. The vortex structures re- presented by yellow dots has positive circulation, and those represented by blue dots has a negative one. The boundary line between yellow and blue dots is regarded as a separation line. In that sense, the flow separation from the circular cylinder, apple000, lies at an angle of about 105 degrees from the front stagnation point in Figure 13(f).
Figure 12. Standard deviation of CL fluctuations of the cylinders.
Figure 13. Flow patterns in each hollows. (a) apple025, (b) apple020, (c) apple015, (d) apple010, (e) apple005, (f) apple000 (circle), (g) V-shaped hollow, (h) U-shaped hollow, (i) ‘apple020flat- top’; flat top without hollow attached on the basic form, and (j) ‘apple020flat-front’; flat front without hollow that is flat top model rotated 90 degrees in the ccw.
This figure shows the instantaneous flow field in a state where the separation point varies every second. The time-averaged location from the successive figures is necessary to obtain the mean location of the separation. In general, a hollow or groove facilitates transition from a laminar to a turbulent boundary layer on the cylinder; thus, it delays the separation [6] [7] [20] . The grooves are often attached at a location between 0 degrees of a front stagnation point and 90 degrees of the top of the circular cylinder. The reason for this is that the grooves have been considered as a kind of promotor for flow transitions if the Reynolds number is high enough to change the state of flow near the critical value. If so, grooves, as an effective promotor, only trigger transition from a laminar to turbulent boundary layer. Thus, the reduction in drag should be about 50% because of turbulent separation, regardless of the shape of the groove.
Drag reduction has been reported to differ depending on the shape and location of the groove [21] at a Reynolds number 2 × 104. This means that the reduction by the groove at this Reynolds number does not arise from turbulent separation. It is presumed that the vortical structures in the grooves sensitively affect the separation. Close-up figures of the flow in each of the grooves are shown in Figure 13. As seen in Figure 13(e), if the groove at the top of the apple model is small, a compact area with negative vorticity is anchored there. The separation point is located at 80 degrees from the front stagnation point. Thus, the width of the wake becomes larger than that of the circular cylinder, shown in Figure 13(f). The same anchored vortex with negative vorticity in the case of apple010 is seen in Figure 13(d). Its drag coefficient was found to be larger than that of the circular cylinder, as seen in Figure 10. In the case of the drag reductions by apple025, apple020, and apple015, such anchored vortices were not distinct. The blobs with negative vorticity being merged with positive ones blur the vortex structures within the groove. Thus, the flow in the groove stagnates, such that it seems just like a filling in the hollow. Since the shape of the cylinder becomes natural shape by virtue of the flow around it, the separation is delayed and drag is reduced.
The effects of V-shaped grooves of various configurations on both the top and bottom of a cylinder upon drag at Re = 2 × 104 were tested by Munendra et al. [21] . They showed that the V-groove seen in Figure 13(g), for which the depth/diameter ratio of the cylinder equals 0.075 and angle of the V-shape is 110 degrees yields the maximum drag reduction. The V-shape can be expressed by a height/base ratio of 0.35. Our V-shaped hollow was located at 90 degrees from the front stagnation point and has a height/base ratio of 0.313, which yielded a vertex angle of 145 degrees and a depth/di- ameter ratio of 0.125. Thus, our V-groove is slightly offset from the optimum, and so the drag reduction was smaller than its maximum possible value. The separation point seems to be located at 120 degrees, as seen in Figure 13(g); therefore, the drag should be still reduced. A relatively strong vortex with negative vorticity appears in the groove, as seen in Figure 13. This is generated on the front slope of the V-shape and causes a low pressure in the groove. Thus, the separation shear layer is suppressed, reattached behind the rear edge of the V-shaped groove, and separated again at around 120 degrees. The drag reduction by the V-shaped hollow was 5%, as shown in Figure 10.
A 7.6% drag reduction by the U-shaped groove, as shown in Figure 10, is similar to the results numerically obtained by Ladjedel et al. [6] .Their reduction was 9%, but 0.8% by the experiment. The flow in the U-shaped groove, as seen in Figure 13(h), is similar to the open shallow cavity flow [22] . The ratio of depth/length of the cavity, namely, the U-shaped groove in this study, is 0.31. There exist two major vortex structures in the U-shaped groove with this ratio: The front vortex is the primary one with negative vorticity, generated by the separated shear layer from the front edge of the groove. The rear vortex is a secondary one induced by the primary, and so it is weaker than the primary, as indicated by the merging of yellow and blue blobs. Since the balance of the strength of these vorticies influences pressure in the groove, the shear layer separated from the front edge of the groove may reattach at the rear edge if the pressure is low enough to pull into the groove. The reattachment shear layer is separated again at 125 degrees in this study. This is why drag reduction by the U-shaped hollow is slightly larger than that by the V-shaped one. This shows that the depth/length ratio of the hollow affects the drag-reduction performance of the circular cylinder.
6. Conclusion
The drag coefficient of an apple is 0.36, which is 23% less than that of a sphere with the same projected area at a Reynolds number of 6.7 × 104. An apples’ shape must offer a clue to reduce the drag of blunt bodies such as spheres and circular cylinders; thus, the effect of the hollows of an apple on its drag was investigated experimentally and numerically. The flow around the apple was visualized by the hydrogen bubble technique and a three-dimensional numerical simulation using ANSYS FLUENT. The results showed that the width of the wake of the apple was smaller than that of the apple without the hollow. A two-dimensional numerical simulation using the vortex method on the apple-shaped cylinder and the cylinder with several shaped grooves was carried out for investigating the effects of the hollows on the drag reduction of a cylinder. The shape of the model’s groove imitated that of the real apple. The drags of cylinders with several shapes of grooves were obtained numerically and compared with one another. The cylinder with the cross section most similar to an apple attained 13% drag reduction compared with the circular cylinder. It is believed that apple-shaped cross sections offer excellent drag reduction, not only for spheres but also for cylinders.
Cite this paper
Matsumoto, H., Kubota, Y. Ohishi, M. and Mochizuki, O. (2016) Drag on a Cylinder with an Apple- Shaped Cross Section. World Journal of Me- chanics, 6, 323-339. http://dx.doi.org/10.4236/wjm.2016.69024
References
- 1. Malik, A.S., Boyko, O., Atkar, N. and Young, W.F. (2001) A Comparative Study of MR Imaging Profile of Titanium Pedicle Screws. Acta Radiologica, 42, 291-293.
http://dx.doi.org/10.1080/028418501127346846 - 2. Tsutsui, T. and Igarashi, T. (2002) Drag Reduction of a Circular Cylinder in an Air-Stream. Journal of Wind Engineering and Industrial Aerodynamics, 90, 527-541.
http://dx.doi.org/10.1016/S0167-6105(01)00199-4 - 3. Zhou, C.Y., Wang, L. and Huang, W. (2007) Numerical Study of Fluid Force Reduction on a Circular Cylinder Using Tripping Rods. Journal of Mechanical Science and Technology, 21, 1425-1434.
http://dx.doi.org/10.1007/BF03177429 - 4. Hover, F.S., Tvedt, H. and Triantafyllou, M.S. (2001) Vortex-Induced Vibrations of a Cylinder with Tripping Wires. Journal of Fluid Mechanics, 448, 175-195.
http://dx.doi.org/10.1017/S0022112001005985 - 5. Owen, J.C., Bearman, P.W. and Szewczyk, A.A. (2001) Passive Control of VIV with Drag Reduction. Journal of Fluids and Structures, 15, 597-605.
http://dx.doi.org/10.1006/jfls.2000.0358 - 6. Lo, K.W. and Ko, N.W.M. (1995) Effect of Acoustic Excitation on Flow over a Partially Grooved Circular Cylinder. Experiments in Fluids, 19, 194-202.
http://dx.doi.org/10.1007/BF00189708 - 7. Yokoi, Y., Igarashi, T. and Hirao, K. (2011) The Study about Drag Reduction of a Circular Cylinder with Grooves. Journal of Fluid Science and Technology, 6, 637-650.
http://dx.doi.org/10.1299/jfst.6.637 - 8. Seo, S.H., Nam, C.D., Han, J.Y. and Hong, C.H. (2013) Drag Reduction of a Bluff Body by Grooves Laid out by Design of Experiment. Journal of Fluids Engineering, 135, Article ID: 111202.
- 9. Lim, H.C. and Lee, S.J. (2003) PIV Measurements of near Wake behind a U-Grooved Cylinder. Journal of Fluids and Structures, 18, 119-130.
http://dx.doi.org/10.1016/S0889-9746(03)00086-0 - 10. Alonzo-García, A., Gutiérrez-Torres, C. del C. and Jiménez-Bernal, J.A. (2014) Large Eddy Simulation of the Subcritical Flow over a U-Grooved Circular Cylinder. Advances in Mechanical Engineering, 6, 1-14.
- 11. Quintavalla, J.S., Angilella, J.A. and Smits, J.A. (2013) Drag Reduction on Grooved Cylinders in the Critical Reynolds Number Regime. Experimental Thermal and Fluid Science, 48, 15-18.
http://dx.doi.org/10.1016/j.expthermflusci.2013.01.018 - 12. Talley, S. and Mungal, G. (2002) Flow around Cactus-Shaped Cylinders. Annual Research Briefs, 363-376.
- 13. Talley, S., Iaccarino, G., Mungal, G. and Mansour, N.N. (2001) An Experimental and Computational Investigation of Flow Past Cacti. Annual Research Briefs, 51-63.
- 14. Zhou, B., Wang, X., Gho, M.W. and Tan, K.S. (2015) Force and Flow Characteristics of a Circular Cylinder with Uniform Surface Roughness at Subcritical Reynolds Numbers. Applied Ocean Research, 49, 20-26.
http://dx.doi.org/10.1016/j.apor.2014.06.002 - 15. Bruneau, C.-H. and Mortazavi, I. (2008) Numerical Modelling and Passive Flow Control Using Porous Media. Computers & Fluids, 37, 488-498.
http://dx.doi.org/10.1016/j.compfluid.2007.07.001 - 16. Butt, U., Jehring, L. and Egbers, C. (2014) Mechanism of Drag Reduction for Circular Cylinders with Patterned Surface. International Journal of Heat and Fluid Flow, 45, 128-134.
http://dx.doi.org/10.1016/j.ijheatfluidflow.2013.10.008 - 17. Matumoto, H., Kubota, Y., Ohishi, M. and Mochizuki, O. (2016) Relation between Bagging of an Apple and Strong Wind. Transactions of the JSME, 82, 1-8. (In Japanese)
- 18. Spalart, P.R. (1988) Vortex Methods for Separated Flows. NASA Technical Memorandum 100068, 1-66.
- 19. Leonard, A. (1980) Vortex Methods for Flow Simulation. Journal of Computational Physics, 37, 289-335.
http://dx.doi.org/10.1016/0021-9991(80)90040-6 - 20. Hoerner, S.F. (1965) Fluid-Dynamic Drag. Published by the Author, 3-6.
- 21. Ladjedel, A.O., Yahiaoui, B.T., Adjlout, C.L. and Imine, D.O. (2011) Experimental and Numerical Studies of Drag Reduction on a Circular Cylinder. International Journal of Mechanical, Aerospace, Industrial, Mechatronic and Manufacturing Engineering, 5, 905-909.
- 22. Munendra, C.V., Inamdar, A. and Kumar, R. (2015) Numerical Studies of Drag Reduction on Circular Cylinder with V-Grooves. International Journal of Engineering Research and General Science, 3, 290-302.












