World Journal of Mechanics
Vol.05 No.12(2015), Article ID:61925,9 pages
10.4236/wjm.2015.512024
Effects of Radiations and Heat Source/Sink on a Casson Fluid Flow over Nonlinear Stretching Sheet
Chenna Sumalatha, Shankar Bandari
Department of Mathematics, Osmania University, Hyderabad, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 27 August 2015; accepted 13 December 2015; published 16 December 2015

ABSTRACT
The present study deals with the flow over a nonlinearly stretching sheet of Casson fluid with the effects of radiation and heat source/sink. The Casson fluid model is used to characterize the non- Newtonian fluid behaviour. With the help of justified similarity transformations the governing equations were reduced to couple nonlinear ordinary differential equations. The effective nume- rical technique Keller Box method is used to solve these equations. The variations in velocity, temperature profiles were presented with the various values of nonlinear stretching parameter n and Casson parameter b. The nature of Skinfriction and Local nusselt number has presented. Effects of radiation and heat source/sink on temperature profiles have been discussed.
Keywords:
Nonlinear Stretching Sheet, Casson Fluid, Keller Box Method, Radiation, Heat Source/Sink

1. Introduction
In recent decades the scientists and engineers are interested to study the flow caused by steady or unsteady stretching sheets because of its rigorous applications in various engineering fields for eg: Polymer sheet extruded continuously from a dye, cooling of metallic plate in a cooling bath and heat-treated materials that travel between feed and wind-up rolls or on a conveyor belt, etc. The exact solution for the flow due to stretching of flat surface was first obtained by Crane [1] . He was investigated the steady flow of an incompressible viscous fluid over an elastic sheet, where as the flow was caused by the stretching of the sheet in its own plane with a velocity varying linearly with the distance from a fixed point. The solution of the three-dimensional fluid motion caused by the stretching boundary was studied by Wang C.Y. [2] . H. I. Andersson [3] has explained an exact solution of the flow of a viscoelastic fluid past a stretching sheet in the presence of a transverse magnetic field is considered.
All the above studies are considered only for a linear stretching sheet, but it is true that not in all cases the stretching sheet is linear. It was first identified by Gupta and Gupta [4] . The study of heat transfer in a viscous fluid over a non-linearly stretching sheet with viscous dissipation was done by Vajravelu [5] . The flow of an incompressible viscous fluid over a non-linear stretching sheet in the presence of chemical reaction and magnetic field was investigated by Raptis and Perdiks [6] . Cortell [7] explained a numerical analysis for flow and heat transfer in a viscous fluid over a non-linear stretching sheet. The Homotopy perturbation method [HPM] and the pade approximation are employed to investigate the MHD boundary layer flow over a non-linear stretching sheet can be found in refs. [8] [9] . Some important aspects of the flow of various non-Newtonian fluids over a non-linear stretching sheet can be found in article [10] . Very recently Pramanic S. [11] has obtained the solution for Casson fluid flow and heat transfer past an exponentially porous stretching surface in presence of thermal radiation and he found that the effect of increasing values of the Casson parameter is seen to suppress the velocity field. But the temperature is enhanced with increasing Casson parameter. Whereas Krishendu Battacharya [12] worked on MHD Stagnation-Point Flow of Casson Fluid and Heat Transfer over a Stretching Sheet with Thermal Radiation. The unsteady boundary layer flow and heat transfer of a Casson fluid over a moving plat plate with a parallel free stream were studied by Mustafa et al. [13] and they solved the problem an alytically using homotopy analysis method (HAM).Different from stretching sheet the Nadeem S. [14] has obtained the numerical solution for MHD flow of a Casson fluid over an exponentially shrinking sheet. The study on Casson fluid flow on both stretching/ shrinking sheet was done by Bhattacharya [15] . The extension of study on the MHD boundary layer flow with heat and mass transfer of a nanofluid over non-linear stretching sheet can be studied by Mabood [16] . Raftari [17] worked an approximate solution of magnetohydrodyn amic [MHD] boundary layer flow.
Casson fluid is one kind of Non-Newtonian fluid. This behaves like a solid elastic and the yield shear stress exists in the consecutive equation for this fluid. Fredrickson [18] investigated the steady flow of a casson fluid in tube. The analytical solution of the unsteady boundary layer flow and heat transfer of a casson fluid over a moving flat plate with a parallel free stream was studied by Mustafa [19] . The analytical solution of the boundary layer flow of an incompressible viscous fluid over a non-linear stretching sheet was studied by Hayat T. [20] . Fekry M. Hady [21] studied the characteristics of a viscous nanofluid over a non-linearly stretching sheet in the presence of thermal radiation and heat transfer. The effect of transpiration on casson fluid heat transfer toward a linearly stretching surface is reported by S. Mukhopadhyay [22] . Hayat [23] determined the effect of thermal radiation on the flow of a second grade fluid.
Since most of the Fluid flow problems are nonlinear so the methods of solving the nonlinear equations are very important. Till today there are different types of Exact methods. In tradition, the perturbation technique is used to find out the approximations to the nonlinear equation similarly Adomin Methods [24] . Even though there are different kinds of analytical techniques available, there is an importance for Numerical techniques. Ibrahim [25] obtained the numerical solution of the boundary layer flow and heat transfer over non-isothermal stretching sheet in a nano fluid with effect of magnetic field. Mahantesh [26] investigated the effect of thermal radiation and non-uniform heat source/sink as heat transfer of MHD visco elastic boundary layer flow over a stretching surface. Bhattacharyya [27] studied the effect of radiation and heat source/sink on the unsteady boun- dary layer flow and heat transfer past a shrinking sheet with suction/injection. The effect of radiation and heat transfer over unsteady stretching surface is analysed by Mahamed [28] . The effect of radiation on free convection from a porous vertical plate studied by Hossain [29] . The Keller-Box method introduced by Keller [30] is one of the best numerical method basically it’s a mixed finite volume method which consists in taking the average of a conservation law and of the associated constitutive law at the level of the same mesh cell. Sarif [31] worked the numerical solution of the steady boundary layer flow and heat transfer over a stretching sheet with Newtonian heating by using Keller box method. Finally the objective of this paper is to study the effects of radiation and heat source/sink of Casson fluid flow over a nonlinearly stretching sheet. The governing partial differential equations are converted into nonlinear differential equations by using suitable similarity transformations and those equations are then solved by using Keller box method.
2. Mathematical Formulation
The steady two-dimenional incompressible flow of a Casson fluid bounded by a stretching sheet at y = 0 has considered. The flow is confined to y > 0. Here x-, y-axes are the directions of the plate and normal to the plate respectively. The rheological equation of state for an isotropic and incompressible flow of the Casson fluid is given by
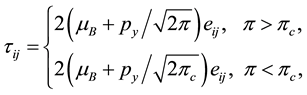
where 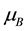 and
and  the plastic dynamic viscosity, yield are stress respectively. Similarly
the plastic dynamic viscosity, yield are stress respectively. Similarly 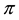 is the product of the component of deformation rate with itself,
is the product of the component of deformation rate with itself,  ,
,  is the (i, j)-th component of the deformation rate and
is the (i, j)-th component of the deformation rate and 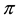 is a critical value of this product based on the non-Newtonian model. Finally the resultant boundary layer equations are
is a critical value of this product based on the non-Newtonian model. Finally the resultant boundary layer equations are
 (1)
(1)
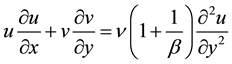 (2)
(2)
 (3)
(3)
where u, v are the velocity components in x, y directions respectively, v is the kinematic viscosity, 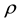 is the density,
is the density,  is the Casson fluid parameter and
is the Casson fluid parameter and  is the thermal diffusivity,
is the thermal diffusivity, 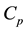 is the specific heat.
is the specific heat.
The suitable boundary conditions are given by
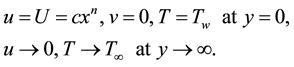 (4)
(4)
Using the Rosseland approximation 






Here, 

With the help of following similarity transformations

The Equations (1), (2) and (3) are transformed in to coupled non linear ordinary differential equations as follows.


and the boundary conditions are transformed into

where 




Hence the dimensionless form of Skin friction 


where 
3. Numerical Discussion
The effect of Radiation parameter

The results obtained with this method agreed with Vajravelu results for Skin friction coefficient 

Figure 1 depicts the variations in Skin friction coefficient with Casson Parameter 
Figure 1. Skin friction coefficient versus Casson parameter β.
Table 1. Variations in f"(0), θ'(0) when Rd = 0, Q = 0.
of nonlinear stretching parameters n. It is noticed that the skin friction coefficient is increased with the increase of 



The nature of velocity profile with variation in non linearly stretching parameter n has been discussed in Figure 3. The velocity of the fluid is found to be decreased with the increase of n. But the decrease of the velocity
profile is negligible for large values of n since the coefficient 

the other hand the temperature increases with increase of n this result is exhibited in Figure 4.
The effect of Casson parameter 
The effect of the Prandtl number on the velocity profile has been depicted in Figure 7. The temperature and the thermal boundary layer thickness decrease with the increase of Pr. Physically it signifies that an increase in
Figure 2. Wall temperature versus Casson parameter β.
Figure 3. Velocity profile with variation in n.
Figure 4. Temperature profile with variation in n.
Figure 5. Velocity profile with variation in β.
Figure 6. Temperature profile with variation in β.
the Prandtl number means an increase of fluid viscosity, which causes a decrease in the temperature distribution.
Figure 8 indicates that the increase of radiation parameter leads to increase in the temperature as well as thermal boundary layer thickness this is because the thermal radiation leads to heat transfer.
Figure 9 depicts the variation of temperature with respect to heat source/sink. It is observed that the increase in heat source/sink parameter increases the temperature profile. This is due to the fact that heat source can add
Figure 7. Temperature profile with variation in Pr.
Figure 8. Temperature profile with variation in Rd.
Figure 9. Temperature profile with variation in Q.
more heat to the stretching sheet which increases its temperature. This increases the thermal boundary layer thickness. In the flow of fluid which reduce the velocity of the flow. In addition to this it is also the velocity approaches to zero as the distance from the sheet increases.
4. Conclusions
The basic governing equations are transformed into coupled nonlinear ordinary differential equations. Keller Box method is used to perform the numerical computations. The effects of nonlinear stretching parameter, Cassson fluid parameter, Prandtl number, radiation parameter and heat source/sink parameters on the heat transfer characteristics are examined with the help of graphs. Finally got an excellent agreement with the previous paper [5] . Briefly the above discussions can be summarized as follows.
1) Both the skin friction coefficient and local Nusselt number increased with the increase in Casson parameter
2) The velocity of the fluid is found to be decrease with the increase in n where as the temperature is increased in this case.
3) The decreasing of momentum boundary layer thickness with the increase in 
4) The increasing effect of the Prandtl decreases the temperature.
5) An increment in the radiation parameter increases the temperature distribution.
6) The increase in the heat source increases the temperature of the fluid.
Cite this paper
ChennaSumalatha,ShankarBandari, (2015) Effects of Radiations and Heat Source/Sink on a Casson Fluid Flow over Nonlinear Stretching Sheet. World Journal of Mechanics,05,257-265. doi: 10.4236/wjm.2015.512024
References
- 1. Crane, L.J. (1970) Flow past a Stretching Plate. Zeitschrift für Angewandte Mathematik und Physik, 21, 645-647.
http://dx.doi.org/10.1007/BF01587695 - 2. Wang, C.Y. (1984) The Three-Dimensional Flow Due to a Stretching Flat Surface. Physics of Fluids, 27, 1915-1917.
http://dx.doi.org/10.1063/1.864868 - 3. Andersson, H.I. (1992) MHD Flow of a Viscoelastic Fluid past a Stretching Surface. Acta Mechanica, 95, 227-230.
http://dx.doi.org/10.1007/BF01170814 - 4. Gupta, P.S. and Gupta, A.S. (1977) Heat and Mass Transfer on a Stretching Sheet with Suction or Blowing. The Canadian Journal of Chemical Engineering, 55, 744-746.
http://dx.doi.org/10.1002/cjce.5450550619 - 5. Vajravelu, K. (2001) Viscous Flow over a Nonlinearly Stretching Sheet. Applied Mathematics and Computation, 124, 281-288.
http://dx.doi.org/10.1016/S0096-3003(00)00062-X - 6. Raptis, A. and Perdikis, C. (2006) Viscous Flow over a Non-Linearly Stretching Sheet in the Presence of a Chemical Reaction and Magnetic Field. International Journal of Non-Linear Mechanics, 41, 527-529.
http://dx.doi.org/10.1016/j.ijnonlinmec.2005.12.003 - 7. Cortell, R. (2007) Viscous Flow and Heat Transfer over a Nonlinearly Stretching Sheet. Applied Mathematics and Computation, 184, 864-873.
http://dx.doi.org/10.1016/j.amc.2006.06.077 - 8. Eerdunbuhe and Temuerchaolu (2012) Approximate Solution of the Magneto-Hydrodynamic Flow over a Nonlinear Stretching Sheet. Chinese Physics B, 21, Article ID: 035201.
http://dx.doi.org/10.1088/1674-1056/21/3/035201 - 9. Ganji, D., Bararnia, H., Soleimani, S. and Ghasemi, E. (2009) Analytical Solution of the Magneto-Hydrodynamic Flow over a Nonlinear Stretching Sheet. Modern Physics Letters B, 23, 2541.
http://dx.doi.org/10.1142/S0217984909020692 - 10. Mukhopadhyay, S. (2013) Casson Fluid Flow and Heat Transfer over a Nonlinearly Stretching Surface. Chinese Physics B, 22, Article ID: 074701.
http://dx.doi.org/10.1088/1674-1056/22/7/074701 - 11. Pramanic, S. (2014) Casson Fluid Flow and Heat Transfer Past an Exponentially Porous Stretching Surface in Presence of Thermal Radiation. Ain Shams Engineering Journal, 5, 205-212.
http://dx.doi.org/10.1016/j.asej.2013.05.003 - 12. Bhattacharyya, K. (2013) MHD Stagnation-Point Flow of Casson Fluid and Heat Transfer over a Stretching Sheet with Thermal Radiation. Journal of Thermodynamics, 2013, Article ID: 169674.
http://dx.doi.org/10.1155/2013/169674 - 13. Mustafa, M., Hayat, T., Pop, I. and Aziz, A. (2011) Unsteady Boundary Layer Flow of a Casson Fluid Due to an Impulsively Started Moving Flat Plate. Heat Transfer, 40, 563-576.
- 14. Nadeem, S., Haq, R.U. and Lee, C. (2012) MHD Flow of a Casson Fluid over an Exponentially Shrinking Sheet. Scientia Iranica, 19, 1550-1553.
http://dx.doi.org/10.1016/j.scient.2012.10.021 - 15. Bhattacharyya, K., Hayat, T. and Alsaedi, A. (2013) Analytic Solution For Magnetohydrodynamic Boundary Layer Flow of Casson Fluid over a Stretching/Shrinking Sheet with Wall Mass Transfer. Chinese Physics B, 22, Article ID: 024702.
http://dx.doi.org/10.1088/1674-1056/22/2/024702 - 16. Mabood, F., Khan, W.A. and Ismail, A.I.M. (2015) MHD Boundary Layer Flow and Heat Transfer of Nanofluids over a Nonlinear Stretching Sheet: A Numerical Study. Journal of Magnetism and Magnetic Materials, 374, 569-576.
http://dx.doi.org/10.1016/j.jmmm.2014.09.013 - 17. Behrouz, R., Syed Tauseef, M.-D. and Ahmet, Y. (2011) Solution to the MHD Flow over a Non-Linear Stretching Sheet Homotopy Perturbation Method. Science China Physics, Mechanics & Astronomy, 54, 342-345.
http://dx.doi.org/10.1007/s11433-010-4180-1 - 18. Fredrickson, A.G. (1964) Principles and Applications of Rheology. Prentice-Hall, Englewood Cliffs.
- 19. Mustafa, M., Hayat, T., Pop, I. and Aziz, A. (2011) Unsteady Boundary Layer Flow of a Casson Fluid Due to an Impulsively Started Moving Flat Plate. Heat Transfer—Asian Research, 40, 563-576.
http://dx.doi.org/10.1002/htj.20358 - 20. Hayat, T., Hussain, Q. and Javed, T. (2009) The Modified Decomposition Method and Pade Approximation for the MHD Flow over a Non-Linear Stretching Sheet. Nonlinear Analysis: Real World Applications, 10, 966-973.
http://dx.doi.org/10.1016/j.nonrwa.2007.11.020 - 21. Hady, F.M., Ibrahim, F.S., Abdel-Gaied, S.M. and Eid, M.R. (2012) Radiation Effect on Viscous Flow of a Nanofluid and Heat Transfer over a Nonlinearly Stretching Sheet. Nanoscale Research Letters, 7, 229.
http://dx.doi.org/10.1186/1556-276X-7-229 - 22. Mukhopadhyay, S., Bhattacharyya, K. and Hayat, T. (2013) Exact Solutions for the Flow of Casson Fluid over a Stretching Surface with Transpiration and Heat Transfer Effects. Chinese Physics B, 22, Article ID: 114701.
http://dx.doi.org/10.1088/1674-1056/22/11/114701 - 23. Hayat, T., Nawaz, M., Sajid, M. and Asghar, S. (2009) The Effect of Thermal Radiation on the Flow of a Second Grade Fluid. Computers & Mathematics with Applications, 58, 369-379.
http://dx.doi.org/10.1016/j.camwa.2009.01.040 - 24. Liao, S.J. (1992) The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. PhD Thesis, Shanghai Jiao Tong University, Shanghai.
- 25. Ibrahim, W. and Shanker, B. (2014) Magnetohydrodynamic Boundary Layer Flow and Heat Transfer of a Nano Fluid over Non-Isothermal Stretching Sheet. Journal of Heat Transfer, 136, Article ID: 051701.
http://dx.doi.org/10.1115/1.4026118 - 26. Nandeppanavar, M.M., Vajravelu, K. and Subhas Abel, M. (2011) Heat Transfer in MHD Viscoelastic Boundary Layer Flow over a Stretching Sheet with Thermal Radiation and Non-Uniform Heat Source/Sink. Communications in Nonlinear Science and Numerical Simulation, 16, 3578-3590.
http://dx.doi.org/10.1016/j.cnsns.2010.12.033 - 27. Bhattacharyya, K. (2011) Effects of Radiation and Heat Source/Sink on Unsteady MHD Boundary Layer Flow and Heat Transfer over a Shrinking Sheet with Suction/Injection. Frontiers of Chemical Science and Engineering, 5, 376-384.
http://dx.doi.org/10.1007/s11705-011-1121-0 - 28. Abd El-Aziz, M. (2009) Radiation Effect on the Flow and Heat Transfer over an Unsteady Stretching Sheet. International Communications in Heat and Mass Transfer, 36, 521-524.
http://dx.doi.org/10.1016/j.icheatmasstransfer.2009.01.016 - 29. Hossain, M.A., Alim, M.A. and Rees, D.A.S. (1999) The Effect of Radiation on Free Convection from a Porous Vertical Plate. International Journal of Heat and Mass Transfer, 42, 181-191.
http://dx.doi.org/10.1016/S0017-9310(98)00097-0 - 30. Keller, H.B. (1971) A New Difference Scheme for Parabolic Problems. In: Hubbard, B., Ed., Numerical Solutions of Partial Differential Equations, Vol. II, Academic Press, New York, 327-350.
- 31. Sarif, N.M., Salleha, M.Z. and Nazar, R. (2013) Numerical Solution of Flow and Heat Transfer over a Stretching Sheet with Newtonian Heating Using the Keller Box Method. Procedia Engineering, 53, 542-554.
http://dx.doi.org/10.1016/j.proeng.2013.02.070













