World Journal of Mechanics
Vol.05 No.06(2015), Article ID:57402,11 pages
10.4236/wjm.2015.56013
Numerical Modeling of Non-Similar Mixed Convection Heat Transfer over a Stretching Surface with Slip Conditions
A. Subba Rao1*, V. R. Prasad1, N. Nagendra1, K. V. N. Murthy1, N. Bhaskar Reddy2, O. Anwar Beg3
1Department of Mathematics, Madanapalle Institute of Technology and Science, Madanapalle, India
2Department of Mathematics, Sri Venkateswara University, Tirupathi, India
3GortEngovation-Aerospace, Medical and Energy Engineering, Bradford, UK
Email: *asrsvu@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 29 April 2015; accepted 22 June 2015; published 25 June 2015
ABSTRACT
In this paper, the heat transfer effect on the steady boundary layer flow of a Casson fluid past a stretching surface in the presence of slip conditions was analyzed. The stretching surface is maintained at a constant temperature. The boundary layer conservation equations, which are parabolic in nature, are normalized into non-similar form and then solved numerically with the well-tested, efficient, implicit, stable Keller-box finite difference scheme. The resulting equations are solved numerically by using the Kellerbox finite-difference method, and the expressions for velocity and temperature are obtained. They satisfy all imposed initial and boundary conditions and reduce to some well-known solutions for non-Newtonian fluids. Numerical results for velocity, temperature, skin friction and Nusselt number are shown in various graphs and discussed for embedded flow parameters. It is found that both velocity and temperature decrease with an increase of the Casson fluid parameter.
Keywords:
Stretching Surface, Non-Newtonian Fluid, Slip Condition, Keller-Box Numerical Method, Heat Transfer, Skin Friction Coefficient

1. Introduction
Heat transfer in non-Newtonian fluids is an important research area due to its wide applications in food processing, petroleum production, cooling of an infinite metallic plate in a cooling bath and in many industries, for example polymers melt, polymer solutions employed in the plastic processing, a long thread traveling between a feed roll and a wind-up roll etc. Flow in the boundary layer on moving solid surface was historically first investigated by Sakiadis [1] [2] who observed that the boundary layer growth was in the direction of motion of the continuous solid surface and deviates from that of the classical Blasius flow past a flat plate. Erickson et al. [3] extended the Sakiadis problem to include blowing or suction at the moving surface and investigated its effects on the heat and mass transfer in the boundary layer. Bijjanal et al. [4] obtained closed-form similarity solutions for steady two-dimensional incompressible boundary layer flow caused by a stretching sheet with Non-Uniform Heat Source/Sink. Combined forced and free convection in boundary layers adjacent to a continuous horizontal sheet maintained at a constant temperature and moving with a constant velocity it was investigated numerically by Chen and Strobel [5] . Grubka and Bobba [6] have investigated the stretching sheet problem for a surface moving with linear velocity and with a variable surface temperature. Dutta et al. [7] studied numerically the Temperature Field in Flow over a Stretching Surface with Uniform Heat Flux. Chen and Char [8] investigated the effects of variable surface temperature and variable heat flux on the heat transfer characteristics of a linearly stretching sheet subject to blowing or suction. Several excellent studies of stretching flows in materials processing were presented by Karwe and Jaluria [9] [10] . Patil et al. [11] further analysed unsteady two- dimensional mixed convection flow along a vertical semi-infinite power law stretching sheet in a parallel free stream with a power-law temperature distribution. Nath et al. [12] analysed the three-dimensional, time dependent stretch surface flow. Ali and Al-Yousef [13] analysed mixed convection heat transfer from a uniformly stretching vertical surface with power function form for wall temperature. Partha et al. [14] described the effects of viscous dissipation on mixed convection heat transfer from an exponentially stretching surface.
Non-Newtonian transport phenomena arise in many branches of chemical and material processing engineering. Such fluids exhibit shear-stress-strain relationships which diverge significantly from the Newtonian (Navier-Stokes) model. Most non-Newtonian models involve some forms of modification to the momentum conservation equations. These include power-law, and thixotropic and viscoelastic fluids (Schowalter [15] ). Such rheological models however cannot simulate the microstructural characteristics of many important liquids including polymer suspensions, liquid crystal melts, physiological fluids, contaminated lubricants, etc. Several fluids in chemical engineering, multiphase mixtures, pharmaceutical formulations, china clay and coal in water, paints, synthetic lubricants, salvia, synovial fluid, jams, soups, jellies, marmalades, sewage sludge etc. are non-Newtonian. The constitutive relations for these kinds of fluids give rise to more complex and higher order equations than the Navier-Stokes equations. Considerable progress has been made on the topic by using different models of non- Newtonian fluids [16] - [25] . Previous studies indicate that not much has been presented yet regarding Casson fluid. This model (Casson [26] ; Nakamura et al. [27] ; Samir Kumar [28] ) in fact is a plastic fluid that exhibits shear thinning characteristics and that quantifies yield stress and high shear viscosity. Casson fluid model is reduced to a Newtonian fluid at a very high wall shear stress, when wall stress is much greater than yield stress. This fluid has good approximations for many substances such as biological materials, foams, molten chocolate, cosmetics, nail polish, some particulate suspensions etc. The boundary layer behaviour of viscoelastic fluid has technical applications in engineering such as glass fibre, paper production, manufacture of foods, the aerodynamic extrusion of plastic sheets, the polymer extrusion in a melt spinning process and many others.
Most of the existing studies on steady boundary layer flow and heat transfer with slip conditions are limited to the non-Newtonian fluid. The considered slip conditions especially are important in the non-Newtonian fluids such as polymer melts which often exhibit wall slip. This motivates us to consider the slip conditions in the present work for non-Newtonian fluids. More exactly, our aim is to investigate steady boundary layer flow and heat transfer of a Casson fluid past a stretching sheet with slip conditions. The equations of the problem are first formulated and then transformed into their dimensionless forms where the Keller box method is applied to find the exact solutions for velocity, temperature, Skin-friction and Nusselt number.
2. Mathematical Analysis
We consider steady two-dimensional laminar mixed convection heat transfer flow along a stretching surface with partial slip. By applying two equal and opposing forces along the x-axis, the sheet is stretched with a speed proportional to the distance from the fixed origin x = 0 as shown in Figure 1. It is also assumed that the external electric field is zero and the electric field due to the polarization of chargers is negligible. The temperature is

Figure 1. (a) Physical model and coordinate system; (b) Grid meshing and a Keller box computational cell.
maintained at prescribed constant value. The fluid properties are assumed to be constant except the density variation in the buoyancy force term.
The rheological equation of state for an isotropic flow of Casson fluid is (Nakamura et al. [27] ):
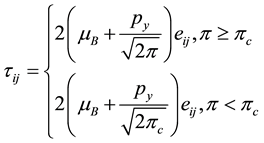 (1)
(1)
in which
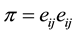 and
and
 represents the
represents the
 component of deformation rate,
component of deformation rate,
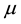 is the dynamic viscosity,
is the dynamic viscosity,
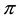 denotes the product of the component of deformation rate with itself,
denotes the product of the component of deformation rate with itself,
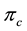 shows a critical value of this product based on the non-Newtonian model,
shows a critical value of this product based on the non-Newtonian model,
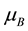 represents the plastic dynamic viscosity of non-Newtonian fluid and
represents the plastic dynamic viscosity of non-Newtonian fluid and
 is the yield stress of fluid.
is the yield stress of fluid.
Under the usual Boussinesq and boundary layer approximations, the equations for mass continuity, (continuity/mass conservation) momentum and energy can be written in the following form:
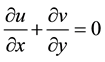 (2)
(2)
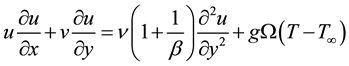 (3)
(3)
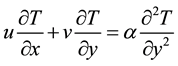 (4)
(4)
where
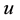 and
and
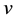 are the velocity components in the
are the velocity components in the
 - and
- and





The boundary conditions are prescribed at the stretching surface and the edge of the boundary layer regime, respectively as follows:

where N0 is the velocity slip factor and K0 is the thermal slip factor. For




where











where U0 is a constant.
In view of Equations (6) and (7), Equations (2)-(4) reduce to the following coupled, nonlinear, dimensionless partial differential equations for momentum and energy for the regime


The transformed dimensionless boundary conditions are:

In the above equations, the primes denote the differentiation with respect to
coordinate, and



dimensional velocity and thermal slip parameters respectively. Here we assumed the typical values K0 = 0.5, N0 = 0.25 for finding the non-dimensional velocity and thermal slip parameters.
The engineering design quantities of physical interest include the skin-friction coefficient and Nusselt number, which are given by:


3. Numerical Solution
In this study the efficient Keller-Box implicit difference method has been employed to solve the general flow model defined by Equations (8)-(9) with boundary conditions (10). Therefore a more detailed exposition is presented here. This method, originally developed for low speed aerodynamic boundary layers by Keller [29] , and has been employed in a diverse range of coupled heat transfer problems. These include Ramachandra Prasad et al. [30] , Rao et al. [31] and Beg et al. [32] .
Essentially 4 phases are central to the Keller Box Scheme.
These are
a) Reduction of the Nth order partial differential equation system to N first order equations;
b) Finite Difference Discretization;
c) Quasilinearization of Non-Linear Keller Algebraic Equations;
d) Block-tridiagonal Elimination of Linear Keller Algebraic Equations.
Phase a: Reduction of the Nth order partial differential equation system to N first order equations
Equations (8)-(9) subject to the boundary conditions (10) are first written as a system of first-order equations. For this purpose, we reset Equations (8)-(9) as a set of simultaneous equations by introducing the new variables u, v and t:





In terms of the dependent variables, the boundary conditions become:

Phase b: Finite difference discretization
A two dimensional computational grid is imposed on the x-η plane as sketched in Figure 2. The stepping process is defined by:


where kn and hj denote the step distances in the ξ and η directions respectively.
If




Figure 2. (a) Influence of Sf on the velocity; (b) Influence of Sf on the temperature.



We now state the finite-difference approximation of Equations (13)-(17) for the mid-point





where we have used the abbreviations



The boundary conditions are

Phase c: Quasilinearization of non-linear Keller algebraic equations
If we assume




Phase d: Block-tridiagonal elimination of linear Keller algebraic equations
The linear system (24)-(28) can now be solved by the block-elimination method, since they possess a block- tridiagonal structure. Commonly, the block-tridiagonal structure consists of variables or constants, but here, an interesting feature can be observed, namely that it consists of block matrices. The complete linearized system is formulated as a block matrix system, where each element in the coefficient matrix is a matrix itself. Then, this system is solved using the efficient Keller-box method. The numerical results are affected by the number of mesh points in both directions. After some trials in the η-direction (radial coordinate) a larger number of mesh points are selected whereas in the ξ direction (tangential coordinate) significantly less mesh points are utilized. ηmax has been set at 10 and this defines an adequately large value at which the prescribed boundary conditions are satisfied. ξmax is set at 3.0 for this flow domain. Mesh independence is therefore achieved in the present com- putations. The computer program of the algorithm is executed in MATLAB running on a PC. The method demonstrates excellent stability, convergence and consistency, as elaborated by Keller [29] and this system is developed by Cebeci and Bradshaw [34] .
4. Results and Discussions
Comprehensive solutions have been obtained and are presented in Figures 2-7. The numerical problem comprises 2 independent variables (x, h), 2 dependent fluid dynamic variables


Figure 3. (a) Influence of ST on the velocity; (b) Influence of ST on the temperature.

Figure 4. (a) Influence of β on the velocity; (b) Influence of β on the temperature.

Figure 5. (a) Effect of Sf on the Skin-friction coefficient results; (b) Effect of Sf on the Nusselt number results.

Figure 6. (a) Influence of ξ on the velocity; (b) Influence of ξ on the temperature.

Figure 7. (a) Influence of Pr on the velocity; (b) Influence of Pr on the temperature.
body force control parameters
In Figure 2(a) and Figure 2(b), the influence of velocity slip parameter on velocity and temperature is illustrated. In Figure 2(a) the dimensionless velocity component at the wall reduces with increase in slip parameter and hence there will be a decrease in the boundary layer thickness. The velocity profiles damped out a bit slower for the high amount of slip parameters, because of an interception which exhibits among them. Figure 2(b) indicates that an increase in slip parameter tends to increase temperature in the flow field. By increasing Sf, thermal boundary layer thickness enhances.
The variation of velocity and temperature with the transverse coordinate (h), over the thermal slip parameter ST is illustrated in Figure 3(a) and Figure 3(b). The response of velocity is much more consistent than for the case of changing velocity slip parameter, it is strongly decreased for all locations in the radial direction. The peak velocity accompanies the case of no thermal slip (ST = 0). The maximum deceleration corresponds to the case of strongest thermal slip (ST = 3). Temperatures (Figure 3(b)) are also strongly depressed with increasing thermal slip. The maximum effect is observed at the wall. Further into the free stream, all temperature profiles converge smoothly to the vanishing value. Figure 4(a) and Figure 4(b) depict the effect of the Casson fluid parameter β on velocity and temperature. Actually, with an increase in non-Newtonian Casson parameter (β), it produces resistance in the fluid flow. An increase in β implies a decrease in yield stress















To validate the present solutions, we compare the present model with the earlier Newtonian model of Merkin [35] and we observe that an excellent agreement between the previous results as shown in Table 1.
5. Conclusions
In this study, numerical solutions have been presented for flow and heat transfer of Casson fluid from a permeable isothermal stretching surface with partial slip. The model has been developed to simulate food stuff transport
Table 1. Values of the local heat transfer coefficient for various values of ξ with β → ∞,
processes in industrial manufacturing operations. A robust, extensively-validated and implicit finite difference numerical scheme has been implemented to solve the transformed and dimensionless velocity and thermal boundary layer equations, subject to physically realistic boundary conditions. The results in summary have shown that, when increasing the velocity slip parameter, velocity, skin friction and Nusselt number decrease, but the temperature increases. A significant finding of this study is that flow separation can be controlled by increasing the value of Casson fluid parameter as well as by increasing Prandtl number.
The current study has been confined to steady-state flow i.e. ignored transient effects and neglected thermal radiation heat transfer effects [36] . Generally, very stable and accurate solutions are obtained with the present finite difference code and it is envisaged that other non-Newtonian flows will be studied using this methodology in the future, including Maxwell upper convected fluids [37] , and couple stress fluids [38] . These aspects are also of relevance to rheological food processing simulations and will be considered in future investigations.
Acknowledgements
The authors are grateful to the reviewers for giving their constructive comments for improving this article. The work is supported by the University Grants Commission-SERO. The authors are thankful to UGC-NEWDELHI, S.V University, Tirupati and management of MITS, Madanapalle.
References
- Sakiadis, B.C. (1961) Boundary-Layer Behavior on Continuous Solid Surfaces: I. Boundary-Layer Equations for Two- Dimensional and Axisymmetric Flow. AIChE Journal, 7, 26-28. http://dx.doi.org/10.1002/aic.690070108
- Sakiadis, B.C. (1961) Boundary-Layer Behavior on Continuous Solid Surfaces: II. Boundary-Layer Equations on a Continuous Flat Surface. AIChE Journal, 7, 221-225. http://dx.doi.org/10.1002/aic.690070211
- Erickson. L.E., Fan. L.T. and Fox, V.G. (1966) Heat and Mass Transfer on Moving Continuous Flat Plate with Suction or Injection. Industrial Engineering Chemistry Fundamentals, 5, 19-25.
- Gireesha, B.J., Roopa, G.S. and Bagewadi, C.S. (2011) Boundary Layer Flow of an Unsteady Dusty Fluid and Heat Transfer over a Stretching Sheet with Non-Uniform Heat Source/Sink. Scientific Research, 3, 726-735. http://dx.doi.org/10.4236/eng.2011.37087
- Chen, T.S. and Strobel, F.A. (1980) Buoyancy Effects in Boundary Layer Adjacent to a Continuous, Moving Horizontal Flat Plate. Journal of Heat Transfer, 102, 170-172. http://dx.doi.org/10.1115/1.3244232
- Grubka, L.J. and Bobba, K.M. (1985) Heat Transfer Characteristics of a Continuous, Stretching Surface with Variable Temperature. ASME J. Heat Transfer, 107, 248-250. http://dx.doi.org/10.1115/1.3247387
- Dutta, B.K., Roy, P. and Gupta, A.S. (1985) Temperature Field in Flow over a Stretching Surface with Uniform Heat Flux. International Communications in Heat and Mass Transfer, 12, 89-94. http://dx.doi.org/10.1016/0735-1933(85)90010-7
- Chen, C.K. and Char, M.I. (1988) Heat Transfer of a Continuous Stretching Surface with Suction or Blowing. Journal of Mathematical Analysis and Applications, 135, 568-580. http://dx.doi.org/10.1016/0022-247X(88)90172-2
- Karwe, M.V. and Jaluria, Y. (1988) Fluid Flow and Mixed Convection Transport from a Moving Plate in Rolling and Extrusion Processes. ASME J. Heat Transfer, 110, 655-661. http://dx.doi.org/10.1115/1.3250542
- Karwe, M.V. and Jaluria, Y. (1991) Numerical Simulation of Thermal Transport Associated With a Continuously Moving Flat Sheet in Materials Processing. ASME J. Heat Transfer, 113, 612-619. http://dx.doi.org/10.1115/1.2910609
- Patil, P.M., Roy, S. and Pop, I. (2010) Unsteady Mixed Convection Flow over a Vertical Stretching Sheet in a Parallel Free Stream with Variable Wall Temperature. International Journal of Heat and Mass Transfer, 53, 4741-4748. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.06.018
- Rajeswari, V., Kumari, M. and Nath, G. (1993) Unsteady Three-Dimensional Boundary Layer Flow Due to a Stretching Surface. Actamechanica, 98, 123-141.
- Ali, M. and Al-Yousef, F. (2002) Laminar Mixed Convection Boundary Layers Induced by a Linearly Stretching Permeable Surface. International Journal of Heat and Mass Transfer, 45, 4241-4250. http://dx.doi.org/10.1016/S0017-9310(02)00142-4
- Partha, M.K., Murthy, P.V.S.N. and Rajasekhar, G.P. (2005) Effect of Viscous Dissipation on the Mixed Convection Heat Transfer from an Exponentially Stretching Surface. Heat and Mass Transfer, 41, 360-366. http://dx.doi.org/10.1007/s00231-004-0552-2
- Schowalter, W.R. (1978) Mechanics of Non-Newtonian Fluids. Pergamon Press, New York.
- Rana, P. and Bhargava, R. (2012) Flow and Heat Transfer of a Nanofluid over a Nonlinearly Stretching Sheet: A Numerical Study. Communications in Nonlinear Science and Numerical Simulation, 17, 212-226. http://dx.doi.org/10.1016/j.cnsns.2011.05.009
- Nazar, M., Fetecau, C., Vieru, D. and Fetecau, C. (2010) New Exact Solutions Corresponding to the Second Problem of Stokes for Second Grade Fluids. Nonlinear Analysis: Real World Applications, 11, 584-591. http://dx.doi.org/10.1016/j.nonrwa.2008.10.055
- Fetecau, C., Hayat, T., Zierep, J. and Sajid, M. (2011) Energetic Balance for the Rayleigh―Stokes problem of an Oldroyd-B fluid. Nonlinear Analysis: Real World Applications, 12, 1-13. http://dx.doi.org/10.1016/j.nonrwa.2009.12.009
- Wang, S.W. and Tan, W.C. (2008) Stability Analysis of Double-Diffusive Convection of Maxwell Fluid in a Porous Medium Heated from Below. Physics Letters A, 372, 3046-3050. http://dx.doi.org/10.1016/j.physleta.2008.01.024
- Tan, W.C. and Xu, M.Y. (2004) Unsteady Flows of a Generalized Second Grade Fluid with the Fractional Derivative Model between Two Parallel Plates. Acta Mechanica Sinica, 20, 471-476.
- Zhang, Z.Y., Fu, C.J., Tan, W.C. and Wang, C.Y. (2007) On Set of Oscillatory Convection in a Porous Cylinder Saturated with a Viscoelastic Fluid. Physics of Fluids, 19, 98-104.
- Rashidi, M.M., Chamkha, A.J. and Keimanesh, M. (2011) Application of Multi-Step Differential Transform Method on Flow of a Second Grade Fluid over a Stretching or Shrinking Sheet. American Journal of Computational Mathematics, 6, 119-128. http://dx.doi.org/10.4236/ajcm.2011.12012
- Ali, N., Hayat, T. and Asghar, S. (2009) Peristaltic Flow of Maxwell Fluid in a Channel with Compliant Walls. Chaos, Solitons & Fractals, 39, 407-416. http://dx.doi.org/10.1016/j.chaos.2007.04.010
- Attia, H.A. and Seddeek, M.A. (2007) On the Effectiveness of Uniform Suction or Injection on Two Dimensional Stagnation-Point Flow towards a Stretching Surface with Heat Generation. Chemical Engineering Communications, 194, 553-564. http://dx.doi.org/10.1080/00986440600992537
- Hussain, M., Hayat, T., Asghar, S. and Fetecau, C. (2010) Oscillatory Flows of Second Grade Fluid in a Porous Space. Nonlinear Analysis: Real World Applications, 11, 2403-2414. http://dx.doi.org/10.1016/j.nonrwa.2009.07.016
- Casson, N. (1959) In Reheology of Dipersed System. Peragamon Press, Oxford.
- Nakamura, M. and Sawada, T. (1988) Numerical Study on the Flow of a Non-Newtonian Fluid through an Axisymmetric Stenosis. Journal of Biomechanical Engineering, 110, 137-143. http://dx.doi.org/10.1115/1.3108418
- Samir Kumar, N. (2013) Analytical Solution of MHD Stagnation-Point Flow and Heat Transfer of Casson Fluid over a Stretching Sheet with Partial Slip. ISRN Thermodynamics, 2013, Article ID: 108264.
- Keller, H.B. (1970) A New Difference Method for Parabolic Problems. In: Bramble, J., Ed., Numerical Methods for Partial Differential Equations, Academic Press, New York, 327-350.
- Prasd, V.R., Vasu, B. and Beg, O.A. (2011) Thermo-Diffusion and Diffusion-Thermo Effects on Boundary Layer Flows. LAP Lambert Academic Publishing GmbH & Co. KG, Saarbrücken.
- Rao, A.S., Prasad, V.R., Reddy, N.B. and Bég, O.A. (2013) Heat Transfer in a Casson Rheological Fluid from a Semi-infinite Vertical Plate with Partial Slip. Heat Transfer-Asian Research, 44, 272-291. http://dx.doi.org/10.1002/htj.21115
- Bég, O.A., Prasad, V.R., Vasu, B., Reddy, N.B., Li, Q. and Bhargava, R. (2011) Free Convection Heat and Mass Transfer from an Isothermal Sphere to a Micropolar Regime with Soret/Dufour Effects. International Journal of Heat and Mass Transfer, 54, 9-18. http://dx.doi.org/10.1016/j.ijheatmasstransfer.2010.10.005
- Prasad, V.R., Rao, A.S., Reddy, N.B., Vasu, B. and Beg, O.A. (2013) Modelling Laminar Transport Phenomena in a Casson Rheological Fluid from a Horizontal Circular Cylinder with Partial Slip. Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering, 227, 309-326. http://dx.doi.org/10.1177/0954408912466350
- Cebeci, T. and Bradshaw, P. (1984) Physical and Computational Aspects of Convective Heat Transfer. Springer, New York. http://dx.doi.org/10.1007/978-3-662-02411-9
- Merkin, J.H. (1977) Free Convection Boundary Layers on Cylinders of Elliptic Cross Section. Journal of Heat Transfer, 99, 453-457. http://dx.doi.org/10.1115/1.3450717
- Prasad, V.R., Vasu, B., Prashad, D.R. and Bég, O.A. (2012) Thermal Radiation Effects on Magneto-Hydrodynamic Heat and Mass Transfer from a Horizontal Cylinder in a Variable Porosity Regime. Journal of Porous Media, 15, 261- 281. http://dx.doi.org/10.1615/JPorMedia.v15.i3.50
- B´eg, O.A. and Makinde, O.D. (2011) Viscoelastic Flow and Species Transfer in a Darcian High-Permeability Channel. Journal of Petroleum Science and Engineering, 76, 93-99. http://dx.doi.org/10.1016/j.petrol.2011.01.008
- Kairi, R.R. and Murthy, P.V.S.N. (2012) Effect of Melting on Mixed Convection Heat and Mass Transfer in a Non-Newtonian Fluid Saturated Non-Darcy Porous Medium. Journal of Heat Transfer, 134, Article ID: 042601.
NOTES
*Corresponding author.



