World Journal of Mechanics
Vol.05 No.05(2015), Article ID:56274,7 pages
10.4236/wjm.2015.55010
Curve Veering in Torsional Systems with Stepped Shafts
Mehdi Eshaghi*, Rama Bhat
Department of Mechanical and Industrial Engineering, Concordia University, Montreal, Canada
Email: *mehdi.eshaghi@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 21 January 2015; accepted 10 May 2015; published 13 May 2015
ABSTRACT
In this study, the influence of geometrical parameters on the curve veering phenomenon in a torsional system with stepped shaft is investigated. Three approximate solutions including finite element, Rayleigh-Ritz and discretization methods, along with an exact solution are employed to obtain the natural frequencies of the structure. The study reveals that, under specific circumstances, the results obtained by approximate methods are very close to the exact solution. The curve veering behavior is manifested irrespective of the method employed. It is concluded that for the structure studied the curve veering behavior is not because of the approximate techniques used to compute the natural frequencies, and is an inherent behavior of the structure.
Keywords:
Curve Veering, Torsional System, Stepped Shaft

1. Introduction
Curve veering is defined as an abrupt veering of the natural frequency plots, when plotted against some system parameters [1] . This phenomenon was reported by Warburton [2] , for the first time. Curve veering was observed, when variation of natural frequencies of the rectangular plate against side ratio was plotted. Leissa [3] observed curve veering in the vibration of square plates. When the variation of natural frequencies against aspect ratio was plotted, it was observed that the curves change smoothly everywhere except in some regions, where they show sudden changes. Leissa called these regions “transition zones” and showed that this behavior is attributed to approximate solution employed for finding the natural frequencies of the structure. The curve veering disappeared when an exact solution was employed. Schajer [4] reported an interesting feature of curve veering in vibration analysis of the vibrating string with a spring support. The study showed that curve veering is not limited to approximate solutions, and it may be an inherent behavior of some vibrating systems. Curve veering as an inherent property of the structure may be seen in rotating disks and plates [5] , clamped beams on intermediate elastic supports [6] and vibration of disordered systems [7] . The significance of curve veering derives from the fact that, a small variation of frequency in the transition zone may yield a sudden change in the vibrational mode. If an external force excites the ith natural frequency of the structure in the transition zone, a small change of excitation frequency causes the (i+1)th frequency of the structure to be excited. As a result, a small change in excitation frequency yields a sudden change in the normal mode of the structure, and the satisfactory performance of the structure may be severely affected. The effect of frequency curve veering in instability of mechanical structures has been widely addressed. For example, mode localization reported in shallow arch [8] , engineering structures [9] and cantilever beam [10] may be regarded as a result of curve veering in these structures. Moreover, estimation and veering analysis of imperfect structures such as cracked plate [11] , nonlinear beam with geometry imperfection [12] and system with gyroscopic coupling [13] have been reported in the literature. It is worth noting that, frequency curve veering may cause localized buckling [14] or wrinkling in specific structures [15] .
In high speed rotating machinery, a considerable number of studies have been carried out on the natural frequencies and mode shapes. Most often, in view of the complex geometry of the rotor systems, they are treated as lumped rotors mounted on shafts. In many practical situations, the shafts may have different cross sections and may have stepped configuration. Accurate determination of the natural frequencies is imperative in order to ensure that the system does not operate near resonant frequencies and particularly in the vicinity of curve veering ranges. Exact solutions are possible only in the case of well-defined uniform shaft geometries, and for practical rotors with many cross sectional changes, approximate techniques such as the discretization method, the Rayleigh Ritz method, finite element method are used. The first general theory for free vibration analysis of torsional systems was reported by Beddoe [16] . A one dimensional wave equation was employed to derive equation of motion of the structure. Maltbeak [17] [18] and Rao [19] studied free torsional vibration of uniform shafts with discrete inertias. Maltbeak assumed a sinusoidal angular displacement along the shaft. Wilson [20] utilized effective inertia method to analyze torsional vibration of a complicated system. To this end, the main structure was divided into some simple sub models, and the sub models were analyzed individually. Finally, Wilson found frequency characteristics of the main structure using a combination of the results obtained from the sub models. Leissa and So [21] applied three dimensional solution for estimation of natural frequencies of the shaft structure.
In the present study, a stepped shaft supporting a rotating disk at the tip is analyzed for its curve veering behavior by computing the natural frequencies by different methods. The effect of geometric parameters of the stepped shaft disk system on the curve veering phenomenon is investigated. Although approximate solutions exhibit curve veering in the structure, an exact method is also employed to confirm this phenomenon as an inherent property of the structure.
2. Mathematical Formulation
An isotropic, homogeneous torsional system composed of a stepped shaft with a lumped disk at the tip, as depicted in Figure 1, is used in the study. The length and diameter of upper and lower shafts are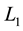 ,
,
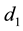 and
and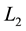 ,
,
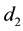 , respectively, and total length of the stepped shaft is L. Moreover, M and d denote the mass and diameter of the lumped disk.
, respectively, and total length of the stepped shaft is L. Moreover, M and d denote the mass and diameter of the lumped disk.
2.1. Exact Solution
The equation of motion of the shaft is given by:
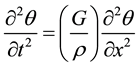 (1)
(1)
where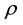 ,
,
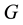 and
and
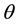 are density, shear modulus and twist angle of the shaft, respectively. The solution of Equation (1) may be found as follows [22] :
are density, shear modulus and twist angle of the shaft, respectively. The solution of Equation (1) may be found as follows [22] :
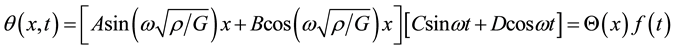 (2)
(2)
where
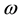 is the frequency of vibration and A, B, C and D are unknown coefficients. The characteristic equation
is the frequency of vibration and A, B, C and D are unknown coefficients. The characteristic equation
Figure 1. Stepped shaft connected to disk.
is obtained by substituting the boundary conditions as:
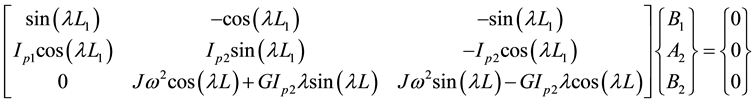 (3)
(3)
where
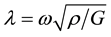 and
and
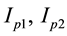 and J are polar moment of inertia of upper shaft, polar moment of inertia of lower shaft and polar mass moment of inertia of the disk, respectively, and
and J are polar moment of inertia of upper shaft, polar moment of inertia of lower shaft and polar mass moment of inertia of the disk, respectively, and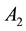 ,
,
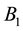 and
and

2.2. The Rayleigh-Ritz Method
In the Rayleigh-Ritz solution, displacement field of a structure is defined as linear combination of admissible functions. In this study, the deflection shape is considered as:

where




where


The conditions for the stationary of the natural frequencies with respect to the arbitrary coefficients in the assumed deflection expression formulate the eigenvalue problem of the structure. It is well-known that the natural frequencies obtained by the Rayleigh-Ritz method are the upper bound. In this study, the following formulation is employed to obtain orthogonal admissible functions [23] .

where


It should be noted that, increasing the number of admissible functions improves the convergence of the results.
2.3. Discretization Method
Discretization technique may be regarded as the simplest, and the least accurate method that is used to find the fundamental frequency of the structure quickly. In this solution, the stiffness constants of the upper and lower shafts are found, individually. Total stiffness of the stepped shaft is obtained as a series combination of these two shaft segments. It should be noted that, solving the problem using this approach necessitates assuming linear torsional deflection through the stepped shaft, while the exact solution reveals trigonometric functions for the shaft deflection. The stiffness constants of the upper and lower shafts are

where



Finally, fundamental frequency of the structure is obtained as:

where

3. Results and Discussion
In this study, the following base line values are assumed in the analysis: shear modulus of the structure is 79.3 Gpa, density is 7800 kg/m3,




3.1. Comparison of the Results
The exact solution for the fundamental frequency of the structure is obtained as 121.022 rad/s. The results obtained by the Rayleigh-Ritz solution reveal that, using one term of admissible function gives fundamental frequency of the structure as 256.88 rad/s. It should be noted that, the admissible functions satisfy the geometric boundary condition, along with continuity of the angular displacement and torque at the point of step change in the shaft cross section. Table 1 shows convergence of the fundamental frequency when the admissible functions satisfy only the geometric boundary conditions. The results given in Table 1 indicate that, they converge to the exact value, although the rate of convergence is poor.
Table 1. Variation of fundamental frequency versus the number of admissible functions in Rayleigh-Ritz method, when d1 = 0.1 m, d2 = 0.05 m, d = 0.5 m and M = 100 kg.
Just using two elements in the finite element model yields the same result as obtained by the exact solution. It is interesting to note that the discretization technique gives fundamental frequency of the structure equal to 121.056 rad/s. The discretization technique considered the displacement field of the structure as a linear function, while the exact solution uses trigonometric functions to describe the displacement field. This is attributed to the magnitude of λ in the exact solution, which has a very small value. In fact, in this order of λ,






3.2. Curve Veering
When the variation of natural frequencies against length ratio




Figure 2. Variation of first five frequencies of the structure versus length ratio when d1 = 0.1 m, d2 = 0.01 m, d = 0.5 m and M = 100 kg.
shows that the number of transition zones increases when mode number increases. For instance, there is just one transition zone in the second mode of vibration, while three, five and seven transition zones may be observed in the third, fourth and fifth vibrational modes, respectively. In order to understand the curve veering phenomenon, transition zone corresponding to the fourth and fifth modes has been magnified. It can be seen that, natural frequencies approach each other and veer away in this region. This behavior is of great significance for the designers.
Table 2 shows the variation of the first five resonant frequencies of the structure, when d1 = 0.1 m, d2 = 0.01 m, d = 0.5 m and M = 100 kg and

Table 2. Variation of first five frequency of the structure versus length ratio, when d1 = 0.1 m, d2 = 0.01 m, d = 0.5 m and M = 100 kg.
Frequency (rad/s)
Figure 3.Variation of first five frequencies of the structure versus length ratio when d1 = 0.1 m, d2 = 0.05 m, d = 0.5 m and M = 100 kg.
Frequency (rad/s)
Figure 4.Variation of first five frequencies of the structure versus length ratio when d1 = 0.1 m, d2 = 0.095 m, d = 0.5 m and M = 100 kg.
4. Conclusion
This study deals with an analysis on the curve veering phenomenon in a torsional structure, which consists of a stepped shaft and a rotating disk. Different approximate techniques including the Rayleigh-Ritz, finite element and discretization methods, along with the exact solution were employed to extract natural frequencies of the structure. The results reveal that curve veering in this structure is not due to application of approximate solution, and it appears even if an exact solution is employed. As a result, the curve veering may be regarded as an inherent behavior of the structure. The geometric parameters affect the curve veering, noticeably. Moreover, a comparison of the results obtained by approximate solutions and those of the exact one was carried out. It was realized that, under some specific geometries and material properties, the frequencies obtained from approximate solutions are as accurate as the exact solution. Under such conditions, the trigonometric functions which describe angular displacement field can be replaced by a linear function.
References
- Bhat, R.B. (1954) Curve Veering Behavior of Some Vibrating Systems. Shock and Vibration, 7, 241-249. http://dx.doi.org/10.1155/2000/841538
- Warburton, G.B. (1974) The Vibration of Rectangular Plates. Shock and Vibration, 8, 371-384.
- Leissa, A.W. (1974) On a Curve Veering Aberration. Journal of Applied Mathematics and Physics (ZAMP), 25, 99-110.
- Schajer, G.S. (1984) The Vibration of a Rotating Circular String Subject to Fixed Elastic Restraint. Journal of Sound and Vibration, 92, 11-19. http://dx.doi.org/10.1016/0022-460X(84)90369-9
- Wang, J.T.S., Shaw, D. and Mahrenholtz, O. (1987) Vibration of Rotating Rectangular Plates. Journal of Sound and Vibration, 112, 455-468. http://dx.doi.org/10.1016/S0022-460X(87)80111-6
- Rao, C.K. (1989) Frequency Analysis of Clamped-Clamped Uniform Beam with Intermediate Elastic Supports. Journal of Sound and Vibration, 133, 502-509. http://dx.doi.org/10.1016/0022-460X(89)90615-9
- Pierre, C. (1988) Mode Localization and Eigenvalue Loci Veering Phenomena in Disordered Structures. Journal of Sound and Vibration, 126, 485-502. http://dx.doi.org/10.1016/0022-460X(88)90226-X
- Breslavsky, I., Avramov, K.V., Mikhlin, Y. and Kochurov, R. (2008) Nonlinear Modes of Snap-Through Motions of a Shallow Arch. Journal of Sound and Vibration, 311, 297-313. http://dx.doi.org/10.1016/j.jsv.2007.09.015
- Chan, H.C. and Liu, J.K. (2000) Mode Localization and Frequency Loci Veering in Disordered Engineering Structures. Chaos, Solitons and Fractals, 11, 1493-1504. http://dx.doi.org/10.1016/S0960-0779(99)00073-9
- Bois, J.L.D., Adhikari, S. and Lieven, N.A.J. (2011) On the Quantification of Eigenvalue Curve Veering: A Veering Index. Journal of Applied Mechanics, 78, 041007-1-041007-8.
- Saito, A., Castanier, M.P. and Pierre, C. (2009) Estimation and Veering Analysis of Nonlinear Resonant Frequencies of Cracked Plates. Journal of Sound and Vibration, 326, 725-739. http://dx.doi.org/10.1016/j.jsv.2009.05.009
- Lacarbonara, W., Arafat, H. and Nayfeh, A.H. (2005) Large Non-Linear Interactions in Imperfect Beams at Veering. International Journal of Non-Linear Mechanics, 40, 987-1003. http://dx.doi.org/10.1016/j.ijnonlinmec.2004.10.006
- Vidoli, S. and Vestroni, F. (2005) Veering Phenomena in Systems with Gyroscopic Coupling. Journal of Applied Mechanics, 72, 641-647. http://dx.doi.org/10.1115/1.1940666
- Chen, J.S. and Li, Y.-T. (2006) Effects of Elastic Foundation on the Snap-Through Buckling of a Shallow Arch under a Moving Point Load. International Journal of Solids and Structures, 43, 4220-4237. http://dx.doi.org/10.1016/j.ijsolstr.2005.04.040
- Al-Qaisia, A.A. and Hamdan, M.N. (2013) On Nonlinear Frequency Veering and Mode Localization of a Beam with Geometric Imperfection Resting on Elastic Foundation. Journal of Sound and Vibration, 332, 4641-4655. http://dx.doi.org/10.1016/j.jsv.2013.03.031
- Beddoe, B. (1965) Wave Theory of Free Torsional Vibration of Composite Systems of Shafts. Journal of Mechanical Engineering Science, 7, 48-56. http://dx.doi.org/10.1243/JMES_JOUR_1965_007_010_02
- Maltbaek, J.C. (1962) Influence of a Discrete Inertia on the Free Torsional Vibrations of a Uniform Bar. International Journal of Mechanical Sciences, 4, 24-34. http://dx.doi.org/10.1016/0020-7403(62)90004-8
- Maltbaek, J.C. (1967) Torsional Vibration of a Stepped Shaft. Engineer, 223, 972-974.
- Rao, D.K. (1978) Torsional Frequencies of a Multi-Stepped Shaft with Rotors. International Journal of Mechanical Sciences, 20, 415-422. http://dx.doi.org/10.1016/0020-7403(78)90031-0
- Wilson, W.K. (1969) Practical Solution of Torsional Vibration Problems. 3rd Edition, Chapman & Hall, London.
- Leissa, A.W. and So, J.Y. (1995) Comparisons of Vibration Frequencies for Rods and Beams from One-Dimensional and Three-Dimensional Analysis. Journal of Acoustic Society, 98, 2122-2135. http://dx.doi.org/10.1121/1.414331
- Thomson, W.T. and Dahleh, M.D. (1997) Theory of Vibrations with Applications. 5th Edition, Prentice Hall, Upper Saddle River.
- Bhat, R.B. (1985) Natural Frequencies of Rectangular Plates Using Characteristic Orthogonal Polynomials in Rayleigh- Ritz Method. Journal of Sound and Vibration, 102, 493-499. http://dx.doi.org/10.1016/S0022-460X(85)80109-7
NOTES
*Corresponding author.










