World Journal of Mechanics
Vol. 3 No. 1 (2013) , Article ID: 27737 , 15 pages DOI:10.4236/wjm.2013.31003
Stability Analysis of Damped Cubic-Quintic Duffing Oscillator
Department of Mathematics, University of Nigeria, Nsukka, Nigeria
Email: *moyesanya@yahoo.com, jnwam2day@yahoo.com
Received November 12, 2012; revised December 14, 2012; accepted December 29, 2012
Keywords: Duffing Oscillator; Cubic-Quintic; Damping; Forcing; Chaos; Derivative Expansion; Stability
ABSTRACT
This paper presents a comprehensive stability analysis of the dynamics of the damped cubic-quintic Duffing oscillator. We employ the derivative expansion method to investigate the slightly damped cubic-quintic Duffing oscillator obtaining a uniformly valid solution. We obtain a uniformly valid solution of the un-damped cubic-quintic Duffing oscillator as a special case of our solution. A phase plane analysis of the damped cubic-quintic Duffing oscillator is undertaken showing some chaotic dynamics which sends a signal that the oscillator may be useful as model for prediction of earthquake occurrence.
1. Introduction
Most real life problems are nonlinear in nature. This has made the study of nonlinear systems which are very complex an important area of study and research. The Duffing oscillator is one of such important nonlinear system.
System (2) below describes the motion of the cubic Duffing oscillator which can be used to model conservative double well oscillators which can occur in magnetoelastic mechanical systems [1]. A good and illustrating example of such system was described in [2]. The cubic Duffing equation can as well be used to model the nonlinear spring-mass system [3,4], as well as the motion of a classical particle in a double well potential [5]. System (2) were proposed by Correig in [6] as a model of microseism time series and have been used in [7] to model the prediction of earthquake occurrence. It was also used to model the transverse oscillation of nonlinear beams in [8].
Generally, the Duffing oscillator can be described by the following equation of motion:
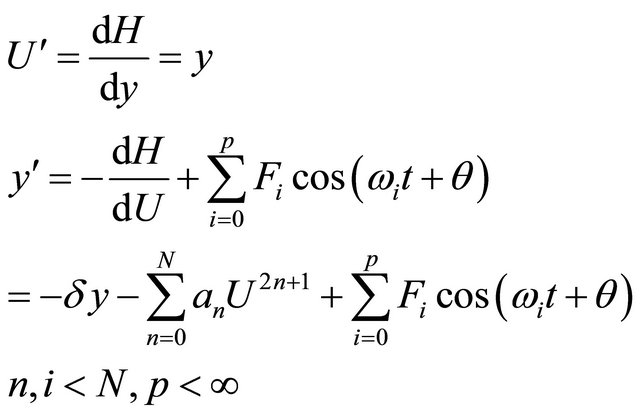 (1)
(1)
where,  are arbitrary positive or negative constants
are arbitrary positive or negative constants

Is the Hamiltonian, 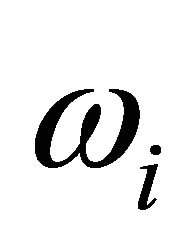 is angular frequency and
is angular frequency and 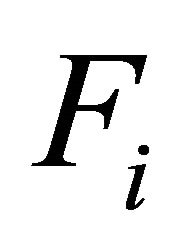 is the amplitude of the harmonic external periodic force.
is the amplitude of the harmonic external periodic force.
If we set 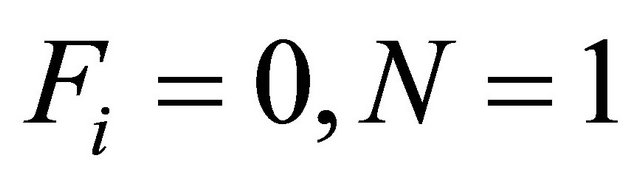 in (1), we obtain,
in (1), we obtain,
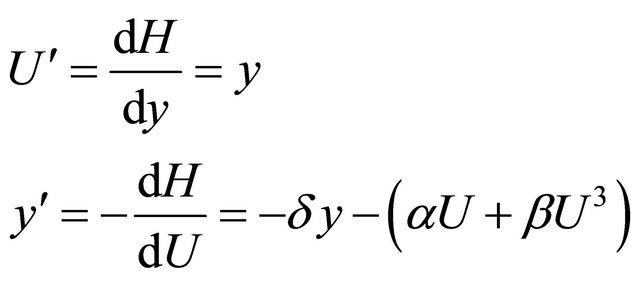 (2)
(2)
and the Hamiltonian becomes
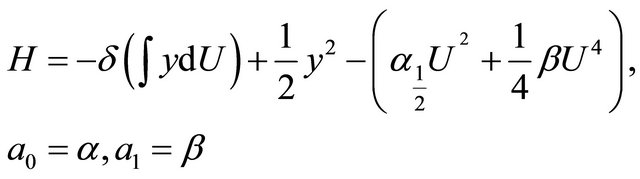
Generally, the damped and forced cubic-quintic Duffing oscillator with random noise obtained by setting  in (1) is given by the equation
in (1) is given by the equation
 (3)
(3)
where, . Here
. Here ![]() is the damping coefficient,
is the damping coefficient, ![]() is the proper or resonant frequency, while β and µ are the coefficient of nonlinearity.
is the proper or resonant frequency, while β and µ are the coefficient of nonlinearity.  is the random noise.
is the random noise.
We can write (3) as a system in the form,
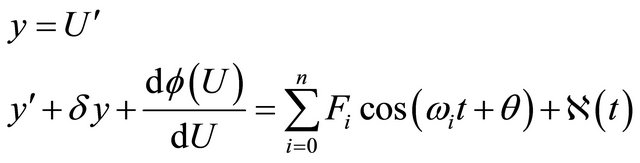 (4)
(4)
where,

is a tri-stable potential or a triple well potential.
Setting 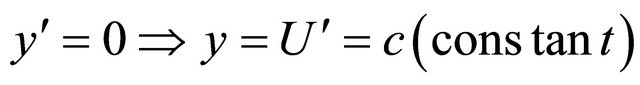 in Equation (4), then we get
in Equation (4), then we get
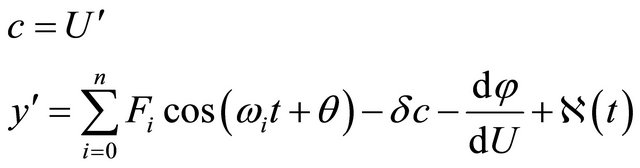 (5)
(5)
where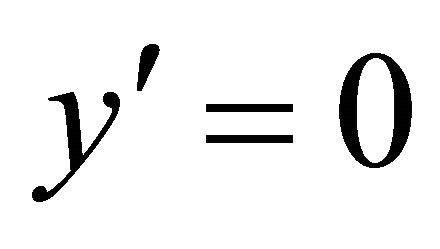 implies, from (4),
implies, from (4),
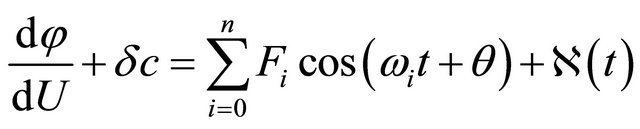 (6)
(6)
The stability matrix of the system (4) is given by,
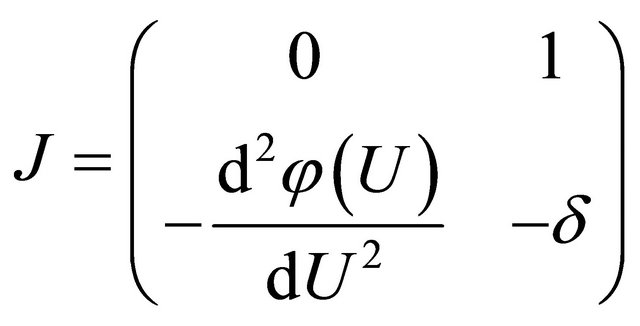 (7)
(7)
The corresponding characteristic equation given by det.  is
is
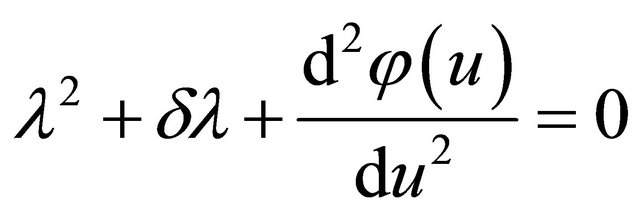 (8)
(8)
2. Perturbative Analysis
Many applied mathematicians have applied the different versions of the multi-scale method which includes the derivative expansion method to a wide variety of problems in physics, engineering and applied mathematics obtaining valid, useful and good results as in [9-14]. The versatility of the derivative expansion method is exhibited where other multiple-scales approach for finding approximate solutions to nonlinear differential equations fails as noted in [15].
Here, we use the derivative expansion method to obtain three-term uniformly valid approximate solution of the slightly damped 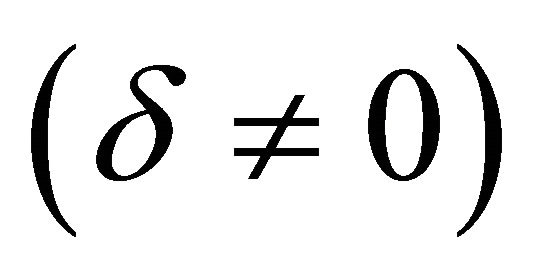 and forced cubic-quintic Duffing equation.
and forced cubic-quintic Duffing equation.
Presently, it is not possible to obtain an exact solution to nonlinear differential equations like our cubic-quintic Duffing oscillator. But, over the years, applied mathematicians have developed methods used successfully to obtain good approximate solutions to these nonlinear differential equations. Among these methods are the perturbation methods like, the method of averaging with its versions, Linstedt-Poincare’s method, Lighthill technique, matched asymptotic methods, multi-scale method with its versions, homotopy perturbation method [16-18], nonperturbative methods [19,20] like, the global error minimization method (GEM) [21], the variational approach [22,23], variational iteration method [24,25], homotopy analysis method [26] and the energy balancing method [27], cubication method [28], and Newton-harmonic balancing method [29].
The method of averaging which is a powerful perturbation method in which solutions of autonomous dynamical systems can be used to approximate solutions of complicated time-varying dynamical systems as mentioned in [30], as well as the Linstedt-Poincare method has been used in to obtain a two-term uniformly valid approximate solution of the un-damped and slightly forced cubic-quintic Duffing equation.
Consider the slightly damped and forced cubic-quintic Duffing equation given by,
 (9)
(9)
where, 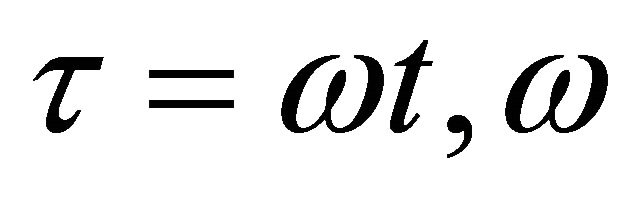 is the natural frequency, ε is a very small term,
is the natural frequency, ε is a very small term, 
We assume that the solution to (9) can be written in the form,
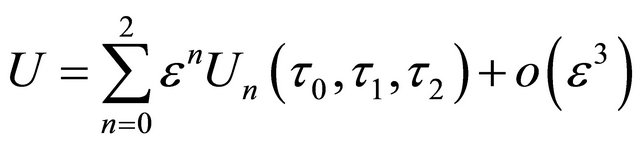 (10)
(10)
where 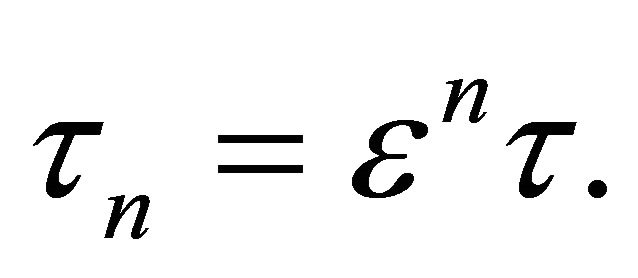
Let
 (11)
(11)
so that,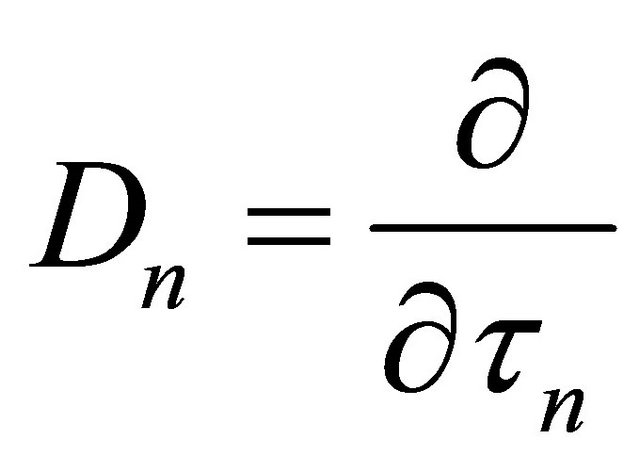 .
.
Substituting (10) and (11) into (9) and equating the coefficient of the powers of epsilon to zero, we obtain,
 (12)
(12)
 (13)
(13)
 (14)
(14)
where,
 the linear operator The solution to (12) is given as,
the linear operator The solution to (12) is given as,
 (15)
(15)
where 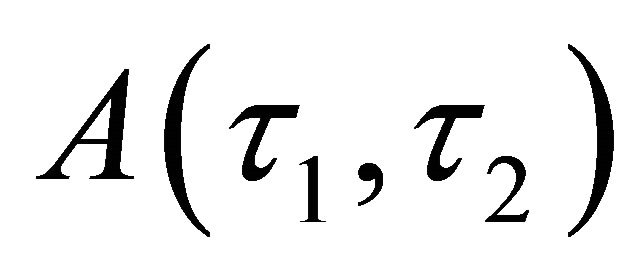 is a complex function and
is a complex function and  is its conjugate.
is its conjugate.
Substituting (15) into (13) and eliminating secular terms, we obtain,
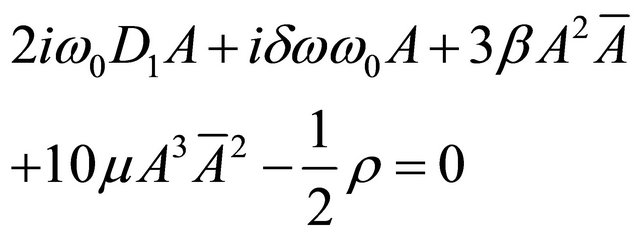 (16)
(16)
and,
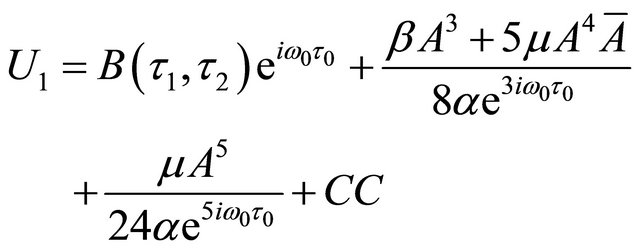 (17)
(17)
where CC denotes complex conjugate.
Solving (16) by letting

with real  we obtain
we obtain
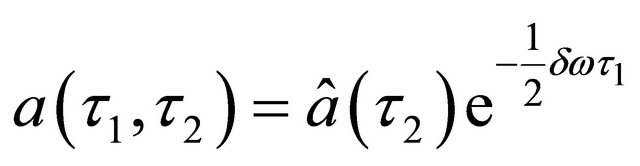
and
 (18)
(18)
Substituting (15) and (17) into (14) and eliminating secular terms, we obtain,
 (19)
(19)
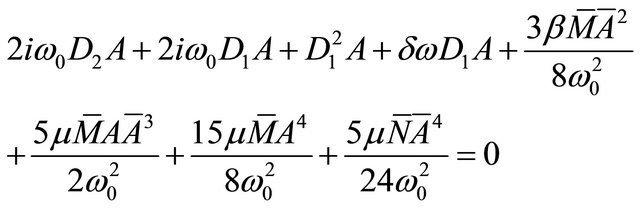 (20)
(20)
where
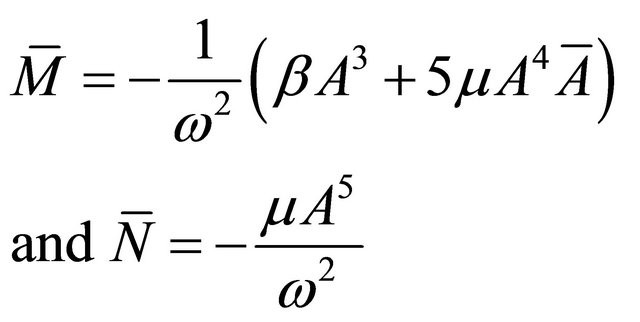 (21)
(21)
Employing (19) in (17) and solving for the third uniformly valid term, we obtain,
 (22)
(22)
where,
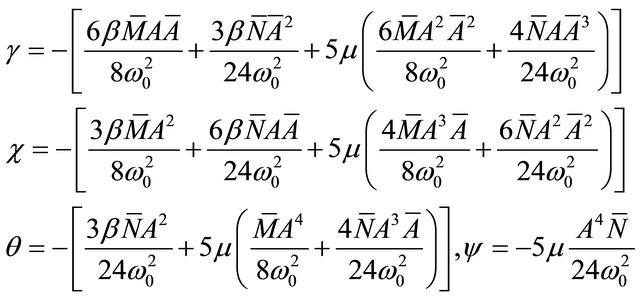
Note that we have used the fact that the complementary function arising from (14) is zero for a uniformly valid solution.
Solving (20) by letting

with real  and
and  and using (18), we obtain,
and using (18), we obtain,

and
 (23)
(23)
where k and  are constants and
are constants and
 .
.
Then using (18) and (23), we obtain,
 (24)
(24)
 (25)
(25)
and U1 in (17) becomes

Using (15), (21), (22) with (23), (24) and (25) the uniformly valid three-term solution to (10) is given by,
 (26)
(26)
where ,the quasi-frequency is given by:
 (27)
(27)
 a constant.
a constant.
For the two-term approximate solution of the undamped and forced cubic-quintic Duffing equation, we set in (26) to obtain,
in (26) to obtain,

(28)
Equation (28) is a valid approximate solution of the un-damped and forced cubic-quintic Duffing oscillator.
3. Stability Analysis
The unforced and damped cubic-quintic Duffing oscillator from (3) is given by,
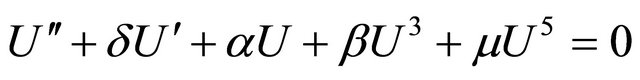 (29)
(29)
From (29), we obtain the autonomous dynamical system,
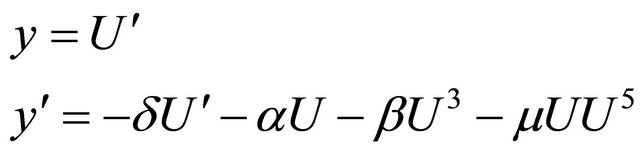
From the condition,  we obtain
we obtain 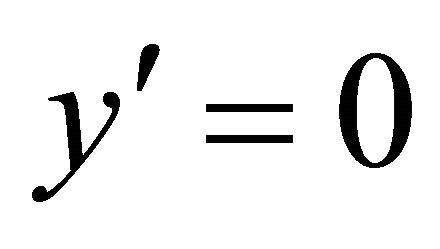 which gives us,
which gives us,
 (30)
(30)
Writing (30) as,
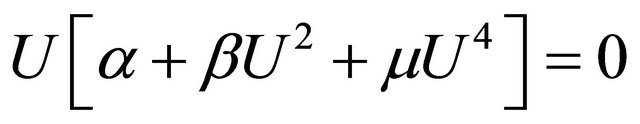 (31)
(31)
We obtain the roots of (31) as,
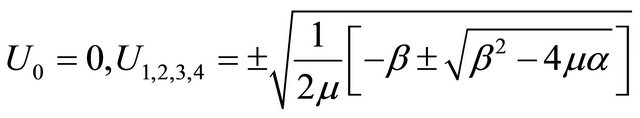 (32)
(32)
Then the equation satisfied by the eigenvalues of our systems stability matrix is,
 (33)
(33)
where 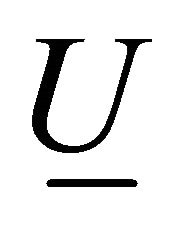 denotes
denotes 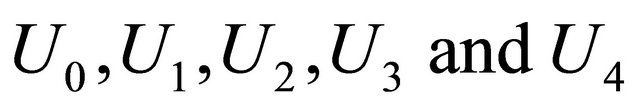 or the
or the 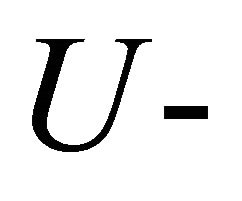 coordinate of an equilibrium point.
coordinate of an equilibrium point.
Whether our eigenvalues will be complex, real or imaginary will be determined by the values of

With . For this we consider the following cases:
. For this we consider the following cases:
1)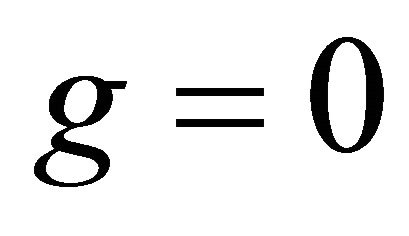 : for this case
: for this case 
This contradicts our assumption that det. 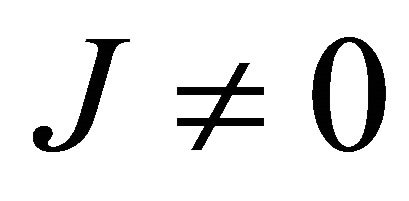 and it also implies that
and it also implies that  are all zero.
are all zero.
2)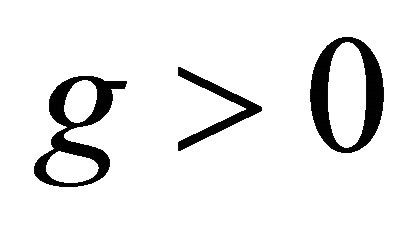 : for this case
: for this case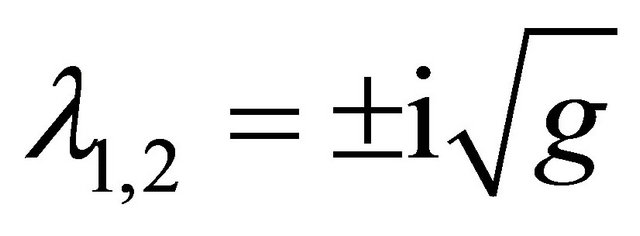 .
.
This corresponds to critical points that are centres for which stability is ensured.
3)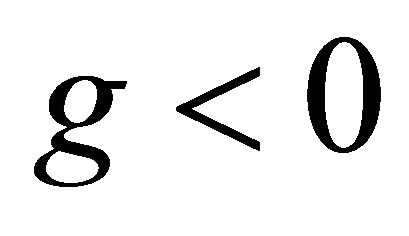 : for this case
: for this case  which corresponds to saddles giving rise to instability [31].
which corresponds to saddles giving rise to instability [31].
With
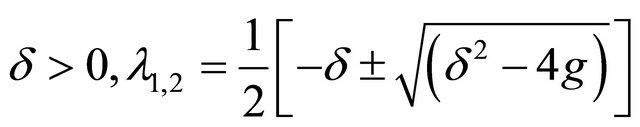 .
.
Then considering the cases below we have:
1)  giving the values
giving the values  which goes contrary to our assumption of det.
which goes contrary to our assumption of det. . It also implies that.
. It also implies that.  are all zero.
are all zero.
2)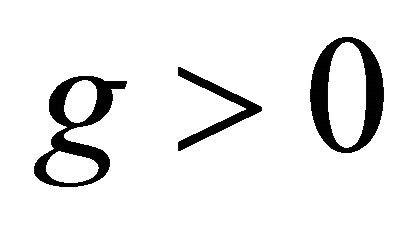 : for this case
: for this case
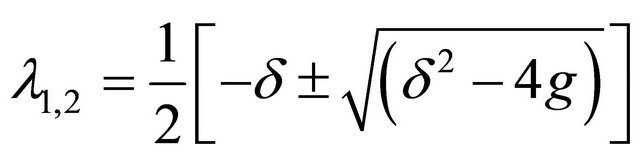
Considering the discriminant for this case, we have the three cases viz,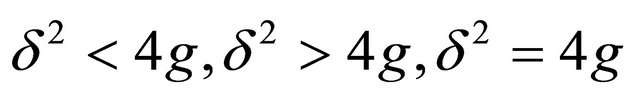 .
.
For the case

which corresponds to spirals and asymptotic stability [32].
The case 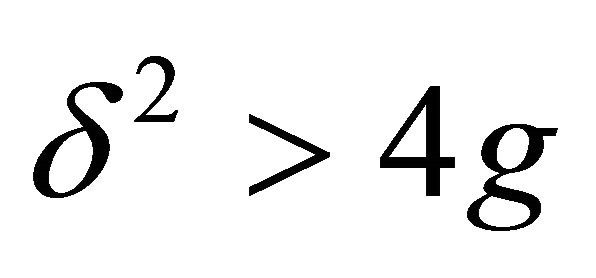 gives values of the form
gives values of the form

which correspond to nodes resulting in asymptotic stability if 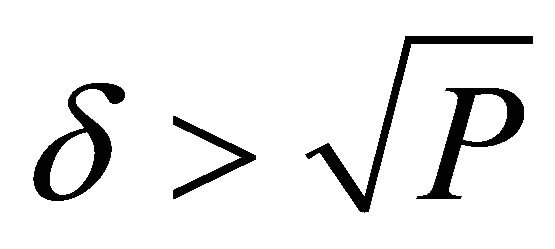 and to saddles and consequent instability if
and to saddles and consequent instability if 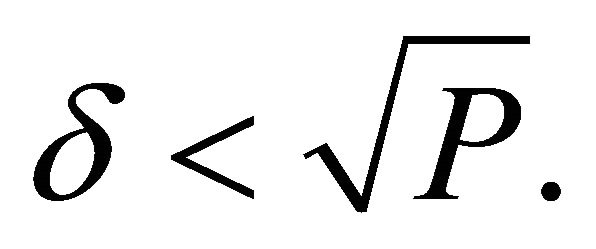
The case 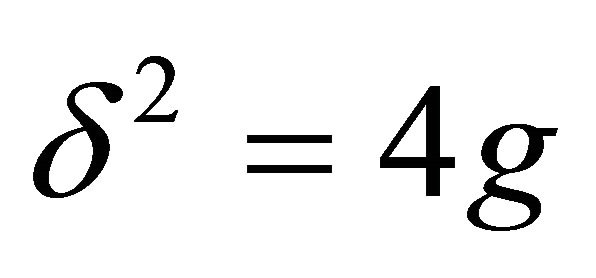 gives
gives 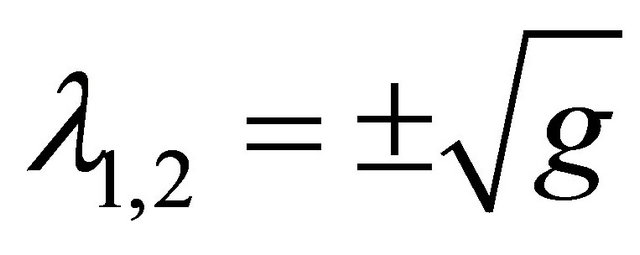
For this case we have saddles and hence instability 3)  lead us to have
lead us to have

Considering the discriminant we consider the three possible cases as follows:
a)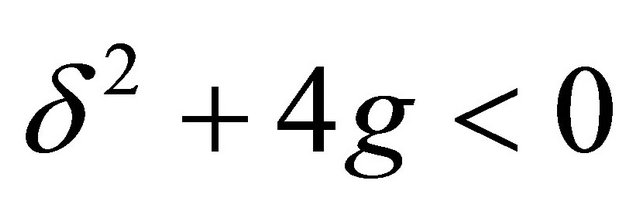 : this case gives
: this case gives
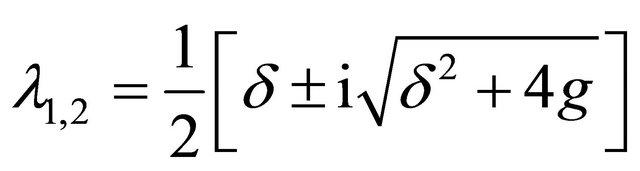
and we have spirals and consequently asymptotic stability (see [31]);
b)  gives
gives
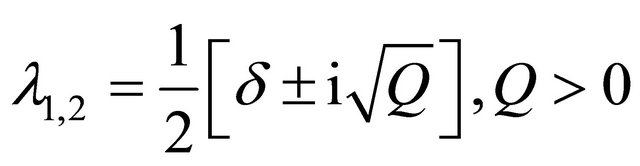
and this leads us to existence of nodes and instability if 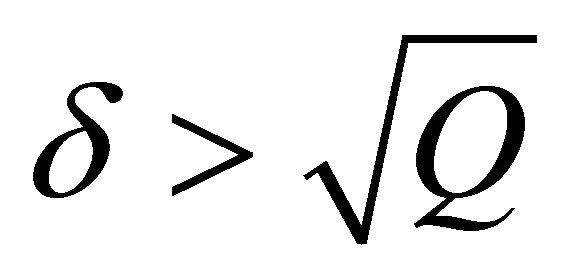 or saddles and instability if
or saddles and instability if 
c)  is the case for which
is the case for which  which yield centres and stability.
which yield centres and stability.
We now consider the stability of the dynamics for a few choices of  employing Equations (32) and (33). In doing this we consider two segments given by
employing Equations (32) and (33). In doing this we consider two segments given by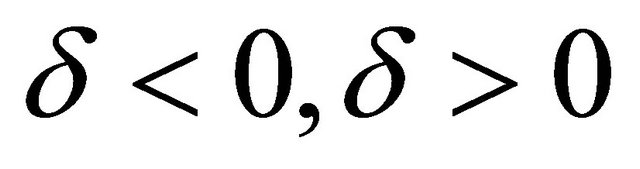 . For each of these segments we treat five cases. Table 1 summarizes the dynamics for the few choices of parameters we used.
. For each of these segments we treat five cases. Table 1 summarizes the dynamics for the few choices of parameters we used.
4. Discussion of Results
Figure 1, is the phase plot showing the behavior of the oscillator when  and
and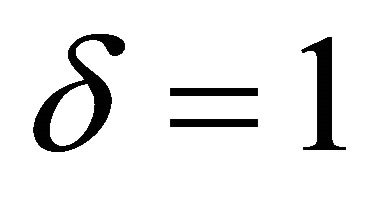 . It is periodic. We observe asymptotically stable spirals at (0, 0) and
. It is periodic. We observe asymptotically stable spirals at (0, 0) and
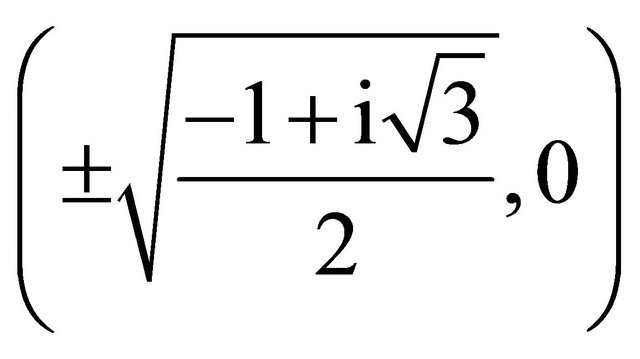
which are the three equilibrium points observed. This situation is seen in the cubic Duffing oscillator.
The phase plot in Figure 2 shows the dynamics of the oscillator when  and
and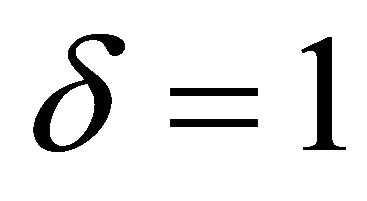 . Five equilibrium points are observed. There exists an asymptotically stable spiral at (0, 0) and unstable saddles at
. Five equilibrium points are observed. There exists an asymptotically stable spiral at (0, 0) and unstable saddles at 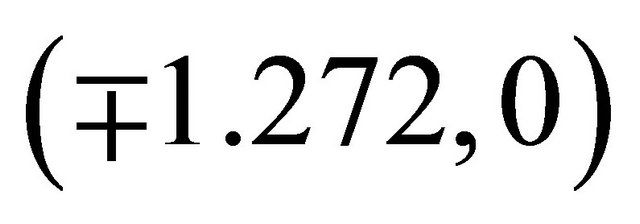 and
and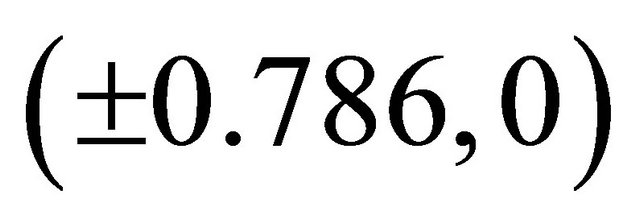 . This situation is not observed in the cubic Duffing oscillator. The five equilibrium points generated is as a result of the presence of the quintic term.
. This situation is not observed in the cubic Duffing oscillator. The five equilibrium points generated is as a result of the presence of the quintic term.
The phase plot in Figure 3 exhibits the behavior of the oscillator when 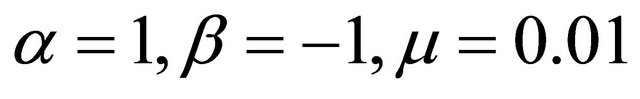 and
and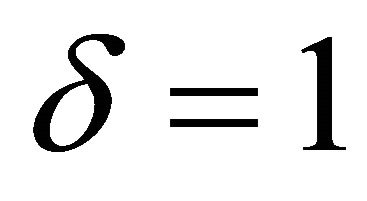 . Five equilibrium points are observed in this phase plot. There exist asymptotically stable spirals at (0, 0) and
. Five equilibrium points are observed in this phase plot. There exist asymptotically stable spirals at (0, 0) and 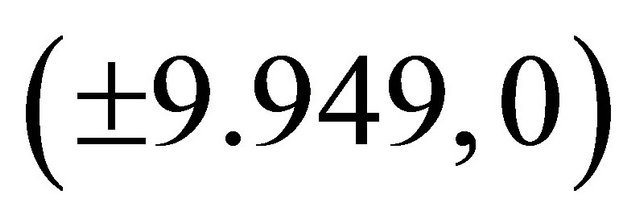 while unstable saddles were obtained at
while unstable saddles were obtained at . This situation cannot occur in the cubic Duffing oscillator. As noted above, it is the addition of the quintic term that allows such situations to occur.
. This situation cannot occur in the cubic Duffing oscillator. As noted above, it is the addition of the quintic term that allows such situations to occur.
The phase plot in Figure 4 exhibits the behavior of the oscillator when 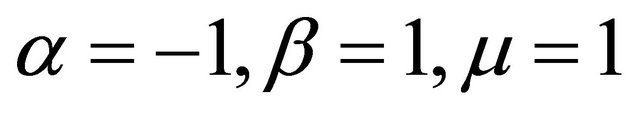 and
and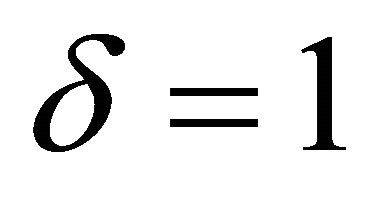 . it is quasi-periodic. Five equilibrium points are observed. There are asymptotically stable spirals at
. it is quasi-periodic. Five equilibrium points are observed. There are asymptotically stable spirals at 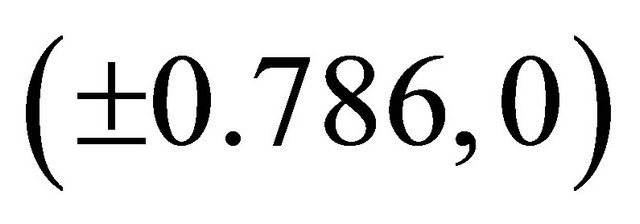 and
and 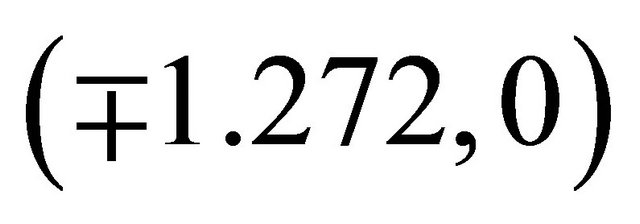 while a saddle exists at (0, 0). As mentioned above, this situation is possible due to the addition of the quintic term. This situation also cannot occur in the cubic Duffing oscillator.
while a saddle exists at (0, 0). As mentioned above, this situation is possible due to the addition of the quintic term. This situation also cannot occur in the cubic Duffing oscillator.
The phase plot in Figure 5 shows the dynamics of the oscillator when 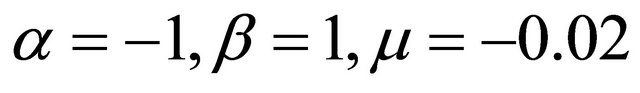 and
and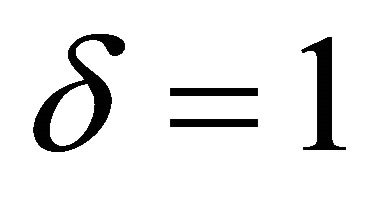 . It is quasi-periodic. Five equilibrium points were also observed. Saddles were obtained at (0,0) and
. It is quasi-periodic. Five equilibrium points were also observed. Saddles were obtained at (0,0) and 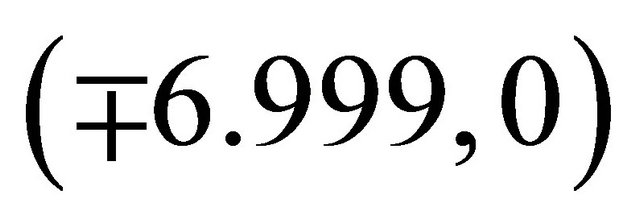 while asymptotically stable spirals are obtained at
while asymptotically stable spirals are obtained at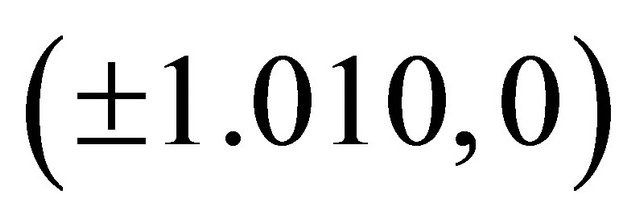 . This situation also cannot occur in the cubic Duffing oscillator, the situation is made possible by the addition of the quintic term.
. This situation also cannot occur in the cubic Duffing oscillator, the situation is made possible by the addition of the quintic term.
Table 1. Stability of the dynamics of the oscillator for few choices of parameter.

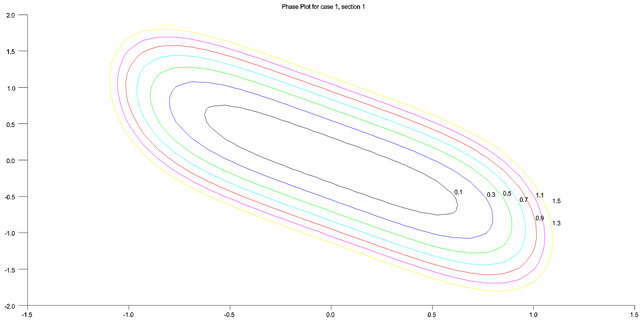
Figure 1. .
.
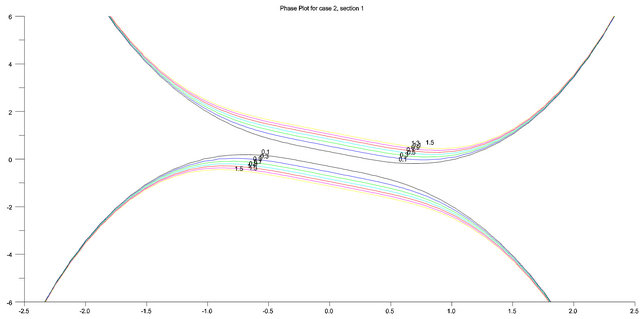
Figure 2. .
.

Figure 3. .
.
The phase plots in Figures 6-10 were obtained for the same values of 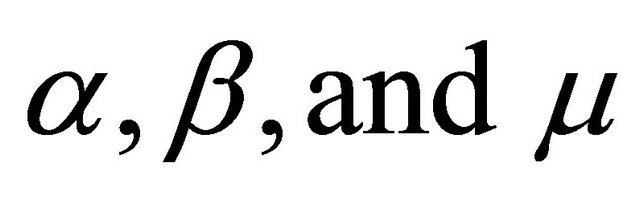 respectively but now with
respectively but now with , the same analysis hold for these cases. It is very important to note that in the phase plots obtained for
, the same analysis hold for these cases. It is very important to note that in the phase plots obtained for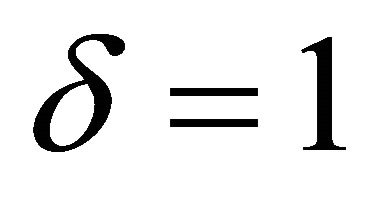 , the phase lines tend to converge (move towards) to the equilibrium points while for
, the phase lines tend to converge (move towards) to the equilibrium points while for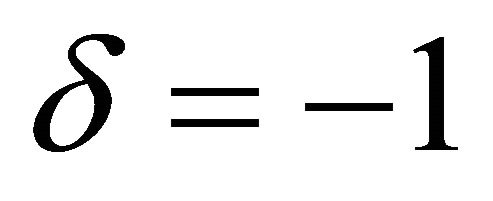 , the phase lines diverge (move away) from the equilibrium points to infinity. This development is in harmony with the solution we obtained in (32) for the damped and forced cubic-quintic Duffing oscillator where, setting
, the phase lines diverge (move away) from the equilibrium points to infinity. This development is in harmony with the solution we obtained in (32) for the damped and forced cubic-quintic Duffing oscillator where, setting , we found out that the exponential function depicting the damping grows larger and tends to infinity. Setting
, we found out that the exponential function depicting the damping grows larger and tends to infinity. Setting , we found out that the exponential function becomes smaller and tends to zero. These results are in line
, we found out that the exponential function becomes smaller and tends to zero. These results are in line

Figure 4. .
.
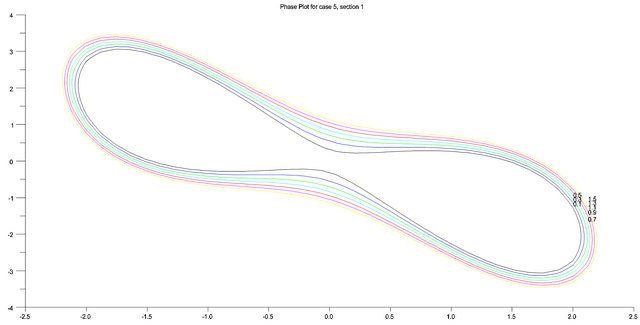
Figure 5. .
.
with observations noted in [33-35] where negative damping effects were observed.
Figure 11 depicts the behavior of the frequency of the unforced and un-damped cubic-quintic Duffing equation obtained using Linstedt-Poincare method (LPM), derivative-expansion method (DEM), homotopy analysis method (HAM) and the method of averaging technique (MOA) for increasing amplitude. Among the three perturbation techniques used, the derivative expansion method agreed most with the homotopy analysis method for small parameters.
In Figures 12 and 13, one observes the dynamics of the damped and forced cubic-quintic Duffing equation as time increases, where we have taken 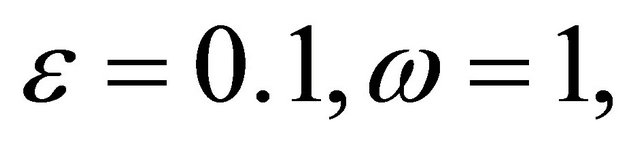
 .
.
Figure 14 shows the periodic displacement of the

Figure 6.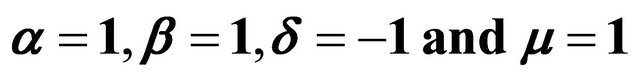 .
.
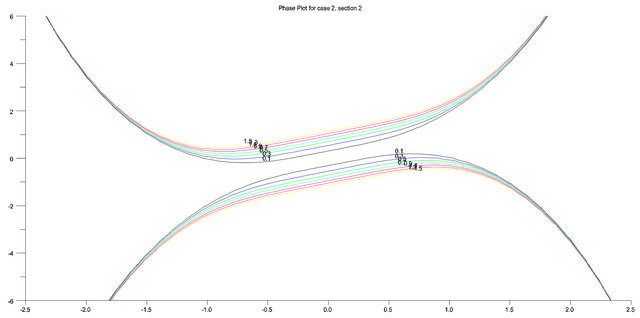
Figure 7.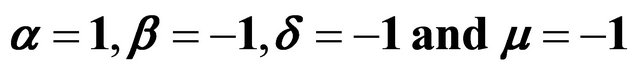 .
.
damped and unforced cubic-quintic Duffing equation as time increases, where we also take 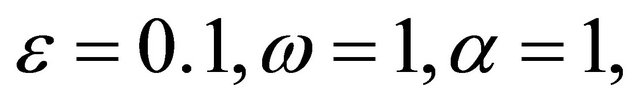
 .
.
Figures 15 and 16 show the periodic displacement of the un-damped and unforced cubic-quintic Duffing equation as time increases, where we also take 
 .
.
The two-term solution to the forced and un-damped cubic-quintic Duffing equation given by
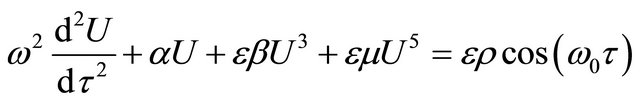
was obtained in [2]. Setting 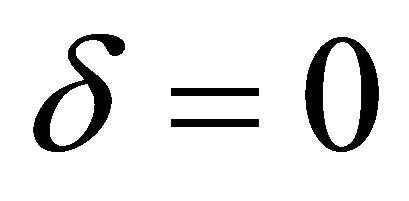 in (26), we obtained (28) with the angular frequency given by
in (26), we obtained (28) with the angular frequency given by
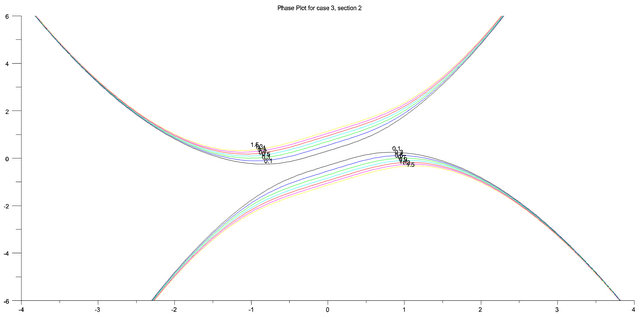
Figure 8.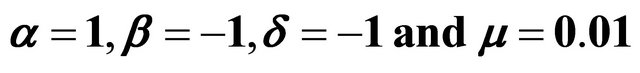 .
.
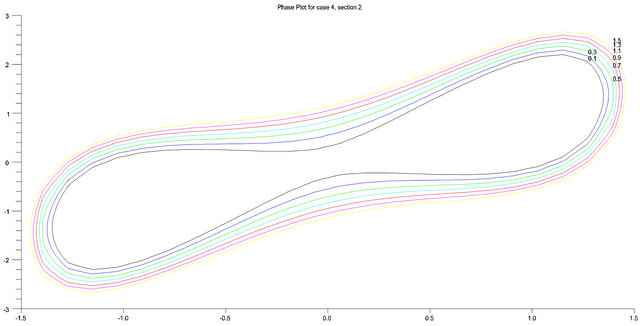
Figure 9. .
.

Setting , we obtained exactly the same results obtained in [2] for the displacement and angular frequency.
, we obtained exactly the same results obtained in [2] for the displacement and angular frequency.
An approximate analytic three-term solution of the un-damped and unforced cubic-quintic Duffing equation was also obtained in [34] using the homotopy analysis method (HAM) and the first-order approximation of the angular frequency was given by
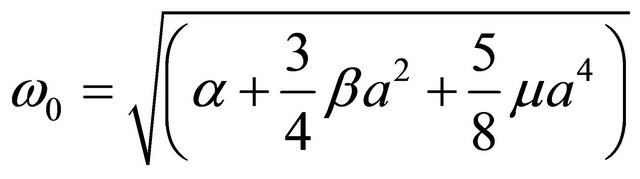 .
.
Expanding this, noting that for small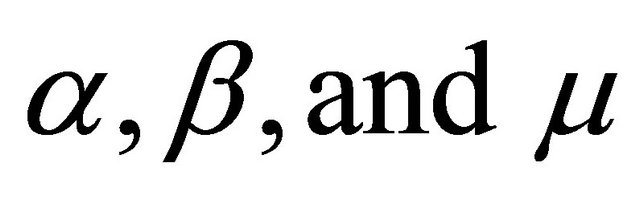 , the first two terms in the expansion were considered and we have,
, the first two terms in the expansion were considered and we have,
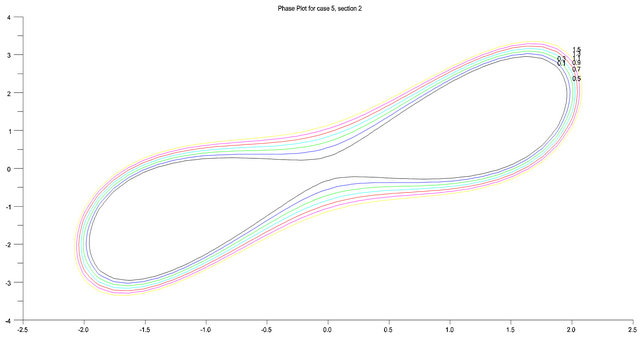
Figure 10. .
.

Figure 11. Behavior of the frequency for increasing amplitude.

where the other terms were considered negligible. Now setting 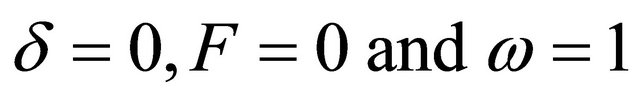 in (27) for
in (27) for 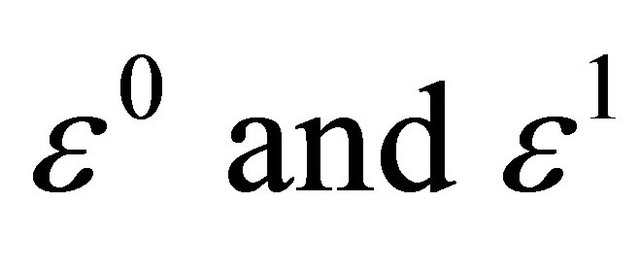 terms, we obtained exactly the value for the angular frequency above.
terms, we obtained exactly the value for the angular frequency above.
5. Conclusion
We investigated the dynamics of the damped and unforced cubic-quintic Duffing oscillator using analytical and perturbative methods, from the analysis done so far and from the tables and phase plots obtained, we observed that the dynamics of the negatively damped and

Figure 12. Behavior of the displacement of the damped and forced cubic-quintic Duffing equation for small time(s) and for,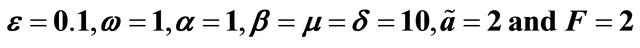 .
.

Figure 13. Behavior of the displacement of the damped and forced cubic-quintic Duffing equation as time(s) increases and for, .
.
unforced cubic-quintic Duffing oscillator remained unstable throughout for the critical points generated by our chosen parameters while that of the positively damped exhibited stability, asymptotic stability as well as instability, thereby pointing to the chaotic behavior of our damped oscillator. We also observed that one, three and

Figure 14. Behavior of the displacement of the damped and unforced cubic-quintic Duffing equation as time(s) increases and for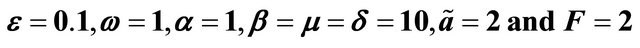 .
.
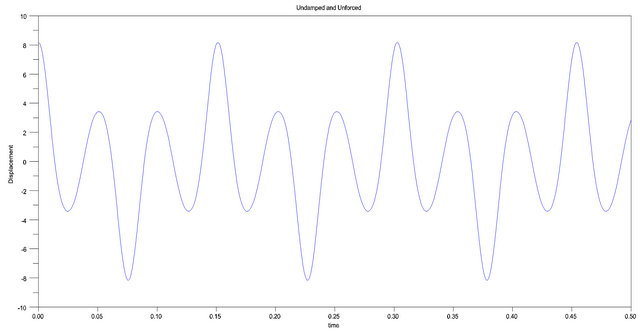
Figure 15. Behavior of the displacement of the unforced and un-damped cubic-quintic Duffing equation for small time(s) and for , .
.
five equilibrium points can be obtained in the simulated phase plots, which was not possible in the cubic Duffing oscillator where only one and three equilibria can be obtained. It can as well be adduced that n-equilibrium points can be obtained by adding nth terms to the cubicDuffing oscillator. We compared our solution to the undamped and forced cubic-quintic Duffing equation as well as the un-damped and un-forced cubic-quintic Duffing equation to those obtained for these cases in [2] and [34] and we got exactly the same results for the displace-

Figure 16. Behavior of the displacement of the unforced and un-damped cubic-quintic Duffing equation for increasing time(s) and for,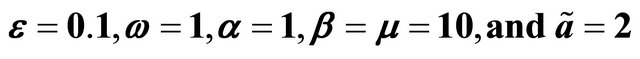 .
.
ment and frequency.We also observed that damping can be represented as an exponential function decaying for 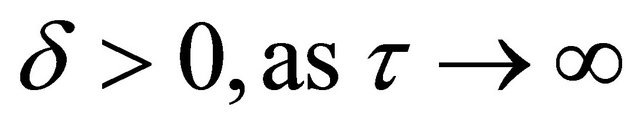 and increasing for
and increasing for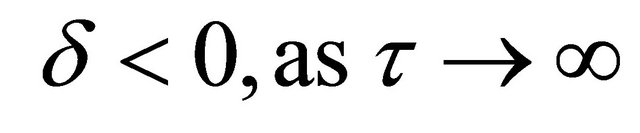 .
.
REFERENCES
- J. Guckenheimer and P. Holmes, “Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields,” In: Applied Mathematical Sciences, Springer-Verlag, New York, 1983.
- V. Chua, “Cubic-Quintic Duffing Oscillators,” 2012. www.its.caltech.edu/mason/research/duf.pdf
- A. Hassan Nayfeh, “Perturbation Methods,” John Wiley & Sons, Inc., Hoboken, 1973.
- J. C. Amazigo, “Postgraduate Lecture Notes on Perturbation Methods,” Department of Mathematics, University of Nigeria, Nsukka, 2011
- R. H. Rand, “Lecture Notes on Nonlinear Vibrations,” 2003. http://www.tam.cornell.edu/randdocs/nlvibe54.pdf
- A. M. Correig and M. Urquizu, “Some Dynamical Aspects of Microseism Time Series,” Geophysical Journal International, Vol. 149, No. 3, 2002, pp. 589-598. doi:10.1046/j.1365-246X.2002.01602.x
- M. O. Oyesanya, “Duffing Oscillator as a Model for Predicting Earthquake Occurrence 1,” Journal of Nigerian Association of Mathematical Physics, Vol. 12, 2008, pp. 133-142.
- H. M. Sedighi, K. H. Shirazi and J. Zare, “An Analytic Solution of Transversal Oscillation of Quintic Nonlinear Beam with Homotopy Analysis Method,” International Journal of Nonlinear Mechanics, Vol. 47, No. 10, 2012, pp. 777-784. doi:10.1016/j.ijnonlinmec.2012.04.008
- J. C. Amazigo, B. Budiansky and G. F. Carrier, “Asymptotic Analyses of the Buckling of Imperfect Columns of Nonlinear Elastic Foundations,” International Journal of Solids and Structures, Vol. 6, No. 10, 1970, pp. 1341- 1356. doi:10.1016/0020-7683(70)90067-3
- J. D. Cole and J. Kevorkian, “Uniformly Valid Asymptotic Approximations for Certain Nonlinear Differential Equations,” In: J. P. Laselle and S. Lefschetz, Eds., Nonlinear Differential Equations and Nonlinear Mechanics, Academic, New York, 1963, pp. 113-120. doi:10.1016/B978-0-12-395651-4.50018-0
- A. H. Nayfeh, “A Comparison of Three Perturbation Methods for the Earth-Moon-Spaceship Problem,” AIAA Journal: The American Institute of Aeronautics and Astronautics, Vol. 3, No. 9, 1965, pp. 1682-1687. doi:10.2514/3.3226
- Y. Y. Shi and M. C. Eckstein, “Ascent or Descent from Satellite Orbit by Low Thrust,” AIAA Journal: The American Institute of Aeronautics and Astronautics, Vol. 4, No. 12, 1966, pp. 2203-2209. doi:10.2514/3.55302
- Y. Y. Shi and M. C. Eckstein, “Application of Singular Perturbation Methods to Resonance Problems,” Astronomical Journal, Vol. 73, 1968, pp. 275-289. doi:10.1086/110629
- H. Ashley, “Multiple Scaling in Flight Vehicle Dynamic Analysis—A Preliminary Look,” AIAA Paper No. 67- 0560.
- L. A. Rubenfeld, “On a Derivative Expansion Technique and Some Comments on Multiple Scaling in the Asymptotic Approximation of Solutions of Certain Differential Equations,” Society for Industrial and Applied Mathematics Review, Vol. 20, No. 1, 1978, pp. 79-105. doi:10.1137/1020005
- J. H. He, “The Homotopy Perturbation Method for Nonlinear Oscillators with Discontinuities,” Applied Mathematics and Computer, Vol. 151, No. 1, 2004, pp. 287-292. doi:10.1016/S0096-3003(03)00341-2
- J. H. He, “Application of Homotopy Perturbation Method to Nonlinear Wave Equations,” Chaos, Solitons and Fractals, Vol. 26, No. 3, 2005, pp. 695-700. doi:10.1016/j.chaos.2005.03.006
- J. H. He, “Homotopy Perturbation Methods for Solving Boundary Value Problems,” Physics Letters A, Vol. 350, No. 1-2, 2006, pp. 87-88. doi:10.1016/j.physleta.2005.10.005
- J. H. He, “New Interpretation of Homotopy Perturbation Method,” International Journal of Modern Physics B, Vol. 20, No. 18, 2006, pp. 2561-2568. doi:10.1142/S0217979206034819
- J. H. He, “Non-Perturbative Methods for Strongly Nonlinear Problems,” Dissertation, De-Verlagim Internet GmbH, Berlin, 2006.
- J. H. He, “A New Perturbation Technique Which Is Also Valid for Large Parameters,” Journal of Sound and Vibrations, Vol. 229, No. 5, 2000, pp. 1257-1263. doi:10.1006/jsvi.1999.2509
- Y. Farzaneh and A. A. Tootoonchi, “Global Error Minimization Method for Solving Strongly Nonlinear Oscillator Differential Equations,” Journal of Computers and Mathematics with Applications, Vol. 59, No. 8, 2010, pp. 2887-2895. doi:10.1016/j.camwa.2010.02.006
- J. H. He, “Variational Approach for Nonlinear Oscillators,” Chaos, Solitons and Fractals, Vol. 34, No. 5, 2007, pp. 1430-1439. doi:10.1016/j.chaos.2006.10.026
- J. H. He, “Variational Principles for Some Nonlinear Partial Differential Equations with Variable Coefficient,” Chaos, Solitons and Fractals, Vol. 19, No. 4, 2004, pp. 847-851. doi:10.1016/S0960-0779(03)00265-0
- J. H. He, “Variational Iteration Method—A Kind of Nonlinear Analytical Technique: Some Examples,” International Journal of Nonlinear Mechanics, Vol. 34, No. 4, 1999, pp. 699-708. doi:10.1016/S0020-7462(98)00048-1
- J. H. He and X. H. Wu, “Construction of Solitary Solution and Compaction-Like Solution by Variational Iteration Method,” Chaos, Solitons and Fractals, Vol. 29, No. 1, 2006, pp. 108-113. doi:10.1016/j.chaos.2005.10.100
- T. Pirbodaghi, S. H. Hoseni, M. T. Ahmadian and G. H. Farrahi, “Duffing Equations with Cubic and Quintic Nonlinearities,” Journal of Computers and Mathematics with Applications, Vol. 57, No. 3, 2009, pp. 500-506. doi:10.1016/j.camwa.2008.10.082
- D. D. Ganji, M. Gorji, S. Soleimani and M. Esmaeilpour, “Solution of Nonlinear Cubic-Quintic Duffing Oscillator Using He’s Energy Balancing Method,” Journal of Zhejiang University Science A, Vol. 10, No. 9, 2009, pp. 1263-1268. doi:10.1631/jzus.A0820651
- A. Belandez, G. Bernabeu, J. Frances, D. I. Mendez and S. Marini, “An Accurate Approximate Solution for the Quintic Duffing Oscillator Equation,” Journal of Mathematical and Computer Modelling, Vol. 52, No. 3-4, 2010, pp. 637-641. doi:10.1016/j.mcm.2010.04.010
- S. K. Lai, C. W. Lim, B. S. Wu, C. Wang, Q. C. Zeng and X. F. He, “Newton-Harmonic Balancing Approach for Accurate Solutions to Nonlinear Cubic-Quintic Duffing Oscillators,” Journal of Applied Mathematical Modelling, Vol. 33, No. 2, 2009, pp. 852-866. doi:10.1016/j.apm.2007.12.012
- R. H. Rand, “Topics in Nonlinear Dynamics with Computer Algebra,” In: Computation in Education, Gordon and Breach Publishers, 1994.
- W. E. Boyce and R. C. Diprima, “Elementary Differential Equations and Boundary Value Problems,” John Wiley & Sons, Inc., Hoboken, 2000.
- E. I. Rivin, “Dynamic Overload and Negative Damping in Mechanical Linkage: Case Study of Catastrophic Failure of Extrusion Press,” Engineering Failure Analysis, Vol. 14, No. 7, 2002, pp. 1301-1312.
- R. D. Peters, “Beyond the Linear Damping Model for Mechanical Harmonic Oscillators,” 2004. http://physics.mercer.edu/petepag/debunk.html.
- S. T. Wu, “Asymptotic Behavior of Solutions for Nonlinear Wave Equations of Kirchoff Type with a PositiveNegative Damping,” Journal of Applied Mathematics Letters, Vol. 25, No. 7, 2012, pp. 1082-1086. doi:10.1016/j.aml.2012.03.022
NOTES
*Corresponding author.

