World Journal of Condensed Matter Physics
Vol.06 No.02(2016), Article ID:66289,12 pages
10.4236/wjcmp.2016.62011
Optimization of Electrics Parameters CdS/CdTe Thin Film Solar Cell Using Dielectric Model
Oumar Absatou Niasse1*, Mahamadou Abdou Tankari2, Fatou Dia1, Nacire Mbengue1, Amadou Diao1, Mamadou Niane1, Moulaye Diagne1, Bassirou Ba1, Gilles Levebvre2
1Laboratory of Semiconductors and Solar Energy, Faculty of Sciences and Technologies, University Cheikh Anta Diop of Dakar, Dakar, Senegal
2University Paris-Creteil, Centre for Studies and Research in Thermal, Environment and Systems (CERTES EA 3481), Paris, France

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 January 2016; accepted 6 May 2016; published 9 May 2016
ABSTRACT
In this paper, the electrical properties of heterojunction solar cells thin film n-CdS/p-CdTe from dielectric model have been studied. Based on the expression of the minority, carriers density in the p-CdTe base of solar cell, the photocurrent density and that of the photo voltage are determined according to the cell dimensions, doping levels, the absorption coefficient, the solar irradiance and the temperature, etc. Fitting using Mathcad and Origin Lab software on the photocurrent and the photovoltage of the n-CdS/p-CdTe enabled to determine the series, shunt resistance and the maximum power point. The results obtained, in good agreement with experimental results, allow operating simulations for optimizing maximum outputs parameters (Ip, Vp). Thereafter, it is proposed a type of photovoltaic generator module with a good command of the design parameters for better efficiency.
Keywords:
Solar Cells, Heterojunction, Series Resistance, Shunt Resistance, Maximum Power Point, Irradiation, Temperature

1. Introduction
The photovoltaic conversion, provided by solar cells, is highly depending on the type of materials and their technologies development. Thin film CdS-CdTe photovoltaic devices are leading technology for high efficiency, and low cost solar modules. Many studies and technical characterization [1] - [5] have been done to control solar cells parameters degradation and maximize the efficiency of energy conversion. In order to reduce the bulk recombination and the cost of solar cells manufacturing for optimal performance, a research in n-CdS/p-CdTe thin films has been started [6] . Both CdTe and CdS are quite stable and can be produced using various scalable techniques like Chemical Both Deposition, Close-space sublimation, Molecular Organic Chemical Vase Deposition (MOCVD), Atomic Layer Epitaxy (ALE), screen printing, sputtering, sintering, Molecular Beam Epitaxy (MBE), Electro-deposition (ED) and High Vacuum Evaporation (HVE) [7] - [9] .
Characterization methods for silicon solar cells are often based on the electrical equivalent circuit. In this work, we have calculated the electrical characteristics I-V directly from photo carrier’s density expressions. From mathematical modeling one-dimensional n-CdS/p-CdTe solar cell, we have established the diffusion equation of the excess minority carriers at the base.
The determination of the density of minority carriers’ expression leads to photocurrent density and photovoltage density in function of doping level, temperature and solar irradiance.
The use of the I-V characteristic allowed us to determine the electrical parameters such as the short-circuit photocurrent, the open circuit photovoltage, series and shunt resistance of the CdS/CdTe solar cell.
2. Preliminaries
Figure 1 shows schematic of n-CdS/p-CdTe solar cell devise structure used in the work, where H is the length of the cell, He, the thickness of the emitter (CdS), Hb the base (CdTe) and W is the width of the depletion zone.
Where,
He is the width of n-CdS emitter; Hb is the width of the p-CdTe base; W is depletion width.
When this solar cell is illuminated along the x-axis (Ox), there is a photo generation and recombination minority carriers in the base part. The minority carrier’s diffusion in steady state is governed by the following diffusion equation:
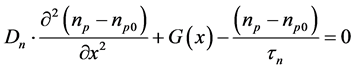 (1)
(1)
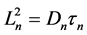 (2)
(2)
where, Ln or Le is the diffusion length of the minority carriers (electrons); Dn is diffusion coefficient, G(x) the recombination rate; τn the lifetime. 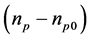 is excess minority carriers density.
is excess minority carriers density.
The solution of Equation (2) is given by:
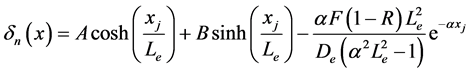 . (3)
. (3)
Figure 1. Schematic representation of a CdS/CdTe solar cell.
The constants A and B Equation (3) were determined using the boundary conditions at the separation surface Junction base:
where 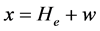 (4)
(4)
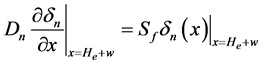 (5)
(5)
At thread side: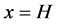 (6)
(6)
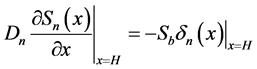 (7)
(7)
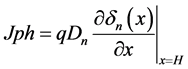 (8)
(8)
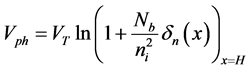 (9)
(9)
where, 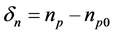 is the excess of the carriers density VT is the thermal voltage, τ is the lifetime, (q) is the electric charge, NA―Acceptor impurity concentration ND―Donor impurity concentration, ni―Intrinsic impurity concentration.
is the excess of the carriers density VT is the thermal voltage, τ is the lifetime, (q) is the electric charge, NA―Acceptor impurity concentration ND―Donor impurity concentration, ni―Intrinsic impurity concentration.
In the photocurrent Equation (8) and photo voltage Equation (9), the absorption coefficient of CdS (αCdS) and absorption coefficient of CdTe (αCdTe) used were determined by dielectric model [10] . In the dielectric function model, Kramer-Kronic, expression is used and developments have led to simple analytical expressions of the real part of the dielectric function and complex. The absorption coefficients of the two semiconductors are based on the past are obtained with band gap energy in the range of 1.1 - 6.1 eV. Figure 2 shows the absorption coefficient calculated by the dielectric model.
Figure 2. Absorption coefficient of CdS (a) and CdTe (b) according to the dielectric model [12] .
3. Results and Discussion
In Figure 3, at the 27˚C temperature and a 750 W/m2 solar irradiance are three main zones on the I-V characteristic of the cell:
-The first zone [0 - 400 mV] corresponds to the short-circuit operating of the cell, where the photo-voltage has no effect on the short-circuit photocurrent,
-The second zone, [400 - 700 mV] to the open circuit operating, where there is no significant photo generated minority carriers that cross the junction, since many of them are stored at the vicinity of the junction.
-The third zone [700 - 800 mV], where the optimum operated joint of the solar cell is localized.
Based on I-V characteristics, a few electrical parameters like series and shunt resistances will be determined according to solar irradiance and temperature.
3.1. Series and Shunt Resistances
The series and shunt resistances can be described as the change of an ideal I-V characteristic. Series resistances, Rs loss is primarily due to the contact resistance of the front and back contacts of the solar cell. Other component that contributes to series resistance is resistance in the semiconductor material. High Rs values lead to a decrease in the FF of the solar cell which in turn affects the efficiency. The shunt resistance, Rsh, is used to model leakage currents. Shunt resistance mainly arises due to leakage current created within a solar cell.
Superimposition actual I-V characteristic is obtained with the ideal characteristic. It’s possible to deduce the series resistance in the area where the solar cell behaves as a voltage generator and the shunt resistance in the wide area of tension, behaves as a current generator.
The ideal characteristic of a solar cell is equivalent to that of an ideal diode with a threshold voltage equal to the short-circuit voltage of the cell, inserted in a circuit supplying with a current equivalent to the short-circuit current. In one hand by plotting the IV characteristic of the solar cell n-CdS/p-CdTe on the same figure as the rectangular ideal characteristic, it is possible to deduce the geometrically shunt resistance and the series resistance.
Figure 3. Method of determining the series resistance and shunt of a solar cell CdS/CdTe 1 cm2.
On the other hand the Origin software we used in the operation of the curves enables a sample “fitting” direct access to the slope (series and shunt conductance) on the previously described zones and hence deduces the series resistance and corresponding shunt. Other studies viewed the equivalent equation of the photovoltaic cell. Additional numerical solution methods for this complex equation allows them to plot the IV characteristic
Our method allows to accurately the value of the shunt resistance and series resistance without using the equation of the equivalent circuit diagram I (V). Table 1 gives the values of these resistances to the solar photocell n-CdS/p-CdTe.
The results obtained are summarized in Table 1, where, Isc is the current of the short-circuit, Vsc is the open circuit photovoltage.
Another experimental method [11] - [13] of series resistance of solar cell by measuring a variation of the illumination is to determine the characteristic of (L2) from the known characteristic of I (L1), as illustrated in Figure 4. Just add to the translation parallel to the ordered, I = I1 − I2, a translation parallel to the abscissa, the numerical application to take account of the voltage drop proportional to the difference of the currents and series resistance. Applying this method to our study, where we have direct two curves with different illumination (500 W/m²) and 800 W/m²), as Table 2 depicted ten values of the cell.
3.2. Photovoltaic Generator
3.2.1. Photovoltaic Module
The solar cell CdS/CdTe obtained in our model has an open circuit voltage of 775 V and a maximum power point of 645 mV. Considering that our PV panel should be able to charge a 12 V battery to its maximum voltage of about 14 V and the overall electrical current-voltage characteristic of the photovoltaic generator therefore theoretically deduced from the combination of the characteristics of 25 supposed identical elementary cells, which make up the two relative affinities 5 parallel to the axis of tension and relative 5 parallel to the axis currents, as illustrated in Figure 6. We consequently obtain the equivalent of modularity by a macro cell whose behavior is identical to the cell. Therefore will loosing 1 to 2 V, wiring and increasing temperature. We expect panel that provides at least 16 - 17 V at maximum power. If we divide 17 by 0.68, we find a round number of 25. This will have solar cells of a module by 5 rows of 5.
3.2.2. Parallel Connection
When the cells are connected in parallel, it is the current to be added and the voltage will remain constant. The properties of parallel cell group are dual to those of series grouping. Thus, in a group of cells connected in parallel, the cells are subjected to the same tension and the resultant characteristic of the group is obtained by
Table 1. Basic parameters for CdTe at different temperatures.
Table 2. Summary of results at two irradiations (500 W m2) and 800 W/m2.
Figure 4. Experimental method to determine shunt resistance and series resistance of the solar cell CdS/CdTe for on 1 cm2.
adding the data voltage to current. Figure 5 shows the resulting feature (Ip, Vp) obtained by combining parallel 5 identical cells. This characteristic is obtained by applying a ratio of affinity 5 on current to the common basic characteristic.
3.2.3. Cells Series Connection
Photovoltaic cells can connect in series. The voltages of all cells are added and the current is the same as that of a single cell (Figure 6). Therefore, always the same cells are connected for the current to series. If one of them was lower in current, it would impose its current throughout the series which would penalize the entire module. It is said pairing in practice. The cells were sorted according to their current to wire them in series. If one of them was lower in current, it would impose its power to the entire series which penalize the entire module.
3.2.4. Impact of Irradiance
The effect of the irradiance on the voltage-current (V-I) and voltage-power (V-P) are shown in Figure 7 and Figure 8. It is noted that the short-circuit current substantially increases with solar irradiation at a given temperature (300 K) when the irradiance varies, the open circuit voltage (Voc) show small variation and the short circuit current Isc varies in proportion to the irradiance. The short-circuit current is increased by 0.39% or 3.9 mA at an irradiance of 1 W/m2.
As far as it the pressure, it is slightly sensitive to light only 0.03% or 0.3 mV of increase is observed for 1 w/m2 and is illustrated in Figure 8.
As it was previously mentioned, the photo-generated current is directly proportional to the irradiance level, so an increment in the irradiation leads to a higher photo-generated current. Moreover, the short circuit current is directly proportional to the photo generated current; therefore it is directly proportional to the irradiance. When the operating point is not the short circuit, in which no power is generated, the photo generated current is also the main factor in the PV current. For this reason the voltage-current characteristic varies with the irradiation. In contrast, the effect in the open circuit voltage is relatively small, as the dependence of the light generated current.
Figure 5. I-V Characteristic of the five CdTe/CdS cell parallel connection.
Figure 6. I-V Characteristic resulting from a parallel from a parallel module for 5 CdS/CdTe Cells.
Figure 7. Impact of the irradiation on the I-V characteristics in the PV module.
Figure 8. Impact of the temperature on the current-voltage characteristic in the PV module.
In Table 3, we present cell parameters electrics at different solar radiation, where, Imax, Vmax are the current and voltage at maximum power, Pmax.
3.2.5. Impact of Temperature
In Figure 8, we notice a very high sensitivity of the open circuit voltage of the temperature variations. When the cell temperature increases, the open circuit voltage decreases substantially, while the short circuit current increases slightly. For cells in CdS/CdTe, the open circuit voltage Voc decrease of about 1.8% for every degree Celsius more increases 0.005% for the same conditions. It may be noted that the PV cells have better performance in cold temperature switch clear skies, instead of a warm and coldly environment.
The temperature (T) has a direct impact on the performance of a solar cell CdS/CdTe as shown in Figure 9.
Generator PV temperature is the result of the ambient temperature and the warming of the cell by the non-absorbed part of the radiation of the cell. Since only a small fraction of the insulations touching the module is converted into electrical power, most of the incident energy is absorbed and converted into heat. Therefore, an indicator called “Nominal Operating Cell Temperature” (

where Em is the irradiance (W/m2).
3.2.6. Optimal Operation of a Photovoltaic Module
The optimum operating point [Vmax(E,T), Imax(E, T)] corresponds to a power of extreme. It is therefore especially geometrically defined by the tangent of the characteristic of panel Ip (Vp) to the hyper bold as the is power is shown in Figure 9 and Figure 10.
The photovoltaic generator (GPV) is subjected to temperature variations at a constant brightness where the maximum power point (MPP) increases steadily with increasing temperature and maximum are on the same straight line.
In Figure 9, the short-circuit photocurrent and photo-voltage increases with solar irradiation. It is noted that the short-circuit photocurrent is more sensitive than the open circuit photo-voltage to increasing radiation.
Table 3. Results for the impact of the solar irradiation.
Figure 9. Impact of the temperature on the characteristic I-V and maximum power in the PV module.
Figure 10. Impact of the irradiation of the characteristic I-V module 300 K.
The tangent to each iso-power corresponding to an I-V characteristic, gives the optimum operating point or the point of maximum operation. The results of Figure 9 are shown in Table 4 where FF is a Fill Factor.
Figure 10 shows the power profile as a function of the photo-voltage for different illuminations. The networks of curves of Figure 10 and Figure 11 show the impedance matching problem depending on the temperature and irradiation.
In particular, for a resistive load it is clear that a perfect impedance matching can be obtained for only one torque value (Temperature-irradiation). We see that the maximum power points lie on a curve, whose shape is pretty close to a straight.
Figure 10 and Figure 11 respectively give the I-V and P-V characteristic of a PV module according to the incident light and at room temperature. We find that changes in short circuit current is proportional to the incident solar flux. Hence the strong influence of irradiation on the current output by the PV module. This influence results in an increase of the power available in the PV modules whenever the illumination increases and each of the luminous flux values is a maximum electric power that could provide a PV module.
The power is the product of voltage and current is the output power delivered by the module. At both ends of the IV curve, output power is zero since either the current or the voltage is zero at these points. The curve of Figure 11 reveals the development of the power as a function of voltage for a solar cell module consisting of 25 n-CdS/p-CdTe for different illuminations. When increasing the illumination, the amplitude of the power increases and the maximum photovoltage moves to large values of photovoltage.
Table 4. Photovoltaic parameters of CdS/CdTe solar cells at 1000 W/m2.
Figure 11. P-V curves of the photovoltaic module for various temperatures.
In the case of energy sources as our solar module n-CdS/p-CdTe this occurs in maximum power points. This type of control is often called in the literature “Maximum Power Point Search” or “Maximum Power Point Tracking” (MPPT) [15] . The principle of these commands is to search the maximum power point (MPP) while ensuring a perfect match between the generator and the load to transfer maximum power.
4. Conclusion
This article is mainly based on the optimization of I-V current voltage characteristics and PV power voltage in the solar cell heterojunction CdS/CdTe. In this model of the dielectric function, we calculated the absorption coefficient of semiconductor components CdS and CdTe. The photocarriers density expression, the photocurrent expression, the photovoltage expression are established in function of the absorption coefficients of CdS and CdTe. The IV and PV characteristics are derived and their exploitation allows to access series resistance and shunt resistance of solar cell CdS/CdTe. In order to confirm the results from the model of the dielectric function, we integrated the intrinsic parameters (Rsh, Rs, Icc, Ico). Therefore the optimization studies made on the silicon solar cells are based on the equation of the equivalent circuit. However in this study, we integrated the intrinsic parameters of the CdS/CdTe cell by establishing the density of photocarriers, the terms of the photocurrent and photovoltage. I-V and P-V characteristics are thus derived and their exploitation has allowed access to the optical and electrical parameters. Finally, considering the climate conditions, the extrinsic parameters offered the perspective to adapt the maximum power point. Specific methods exist to bring devices to operate at maximum points from their specifications without priori that these points are known in advance, and without that we know at what time they are changed or what the reasons of this change are. In the case of energy sources as our solar module n-CdS/p-CdTe, this results in maximum power points. This knowledge allows an optimization of the electrical parameters, which results in a maximum power control at the completion of the solar cell. Thus, in order to confirm the validity of our results, we compared them with those of a reference model and a good match is thus established.
Cite this paper
Oumar Absatou Niasse,Mahamadou Abdou Tankari,Fatou Dia,Nacire Mbengue,Amadou Diao,Mamadou Niane,Moulaye Diagne,Bassirou Ba,Gilles Levebvre, (2016) Optimization of Electrics Parameters CdS/CdTe Thin Film Solar Cell Using Dielectric Model. World Journal of Condensed Matter Physics,06,75-86. doi: 10.4236/wjcmp.2016.62011
References
- 1. Girish Kumar, S. and Koteswara Rao, K.S.R. (2014) Physics and Chemistry of CdTe/CdS Thin Film Heterojunction Photovoltaic Devices: Fundamental and Critical Aspects. Energy & Environmental Science, 7, 45-102.
http://dx.doi.org/10.1039/C3EE41981A - 2. Abdullah, R.A., Razooqi, M.A. and Al-Ajili, AN.H. (2013) Characterization of the Energy Band Diagram of Fabricated on SnO2/CdS/CdTe Thin Solar Cell. International Journal of Mathematical, Computational, Physical and Quantum Engineering, 7, No. 7.
- 3. Williams, B.L., Major, J.D., Bowen, L., Phillips, L., Zoppi, G., Forbes, I. and Durose, K. (2014) Challenges and Prospects for Developing CdS/CdTe Substrate Solar Cells on Mo Foils. Solar Energy Materials & Solar Cells, 124, 31-38.
http://dx.doi.org/10.1016/j.solmat.2014.01.017 - 4. Han, J., Spanheimer, C., Haindl, G., Fu, G., Krishnakumar, V., Schaffner, J., Fan, C., Zhao, K., Klein, A. and Jaegermann, W. (2011) CdTe Thin Film Solar Cells with Reduced CdS Film Thickness. Solar Energy Materials and Solar Cell, 95, 816-820.
http://dx.doi.org/10.1016/j.solmat.2010.10.027 - 5. Mathew, X., Cruz, J.S., Coronado, D.R., Millan, A.R., Segura, G.C., Morales, E.R., Martinez, O.S., Garcia, C.C. and Landa, E.P. (2012) CdS Thin Film Post-Annealing And Te-S Interdiffusion in a CdTe/CdS Solar Cell. Solar Energy, 86, 1023-1028.
http://dx.doi.org/10.1016/j.solener.2011.06.024 - 6. Panchuk, O., Fochuk, P., Triboulet, R. and Siffert, P. (2010) Doping in CdTe and Related Compounds: Physics, Defects, Hetero- and Nano-Structures, Crystal Growth, Surfaces and Applications. Elsevier Ltd., Amsterdam, 309-362.
- 7. Proskuryakov, Y.Y., Durose, K., Major, J.D., Turkestani, M.K.A., Barrioz, V., Irvine, S.J.C. and Jones, E.W. (2009) Doping Levels, Trap Density of States and the Performance of co-Doped CdTe(As,Cl) Photovoltaic Devices. Solar Energy Materials and Solar Cell, 93, 1572-1581.
http://dx.doi.org/10.1016/j.solmat.2009.04.010 - 8. Ferekides, C.S., Goswami, Y., Hakkulov, M.K., Kouchkarov, K.M., Sopain, K., Sulaiman, M.Y. and Ullal, H.S. (2012) Effect of the Composition on Physical Properties of CdTe Absorber Layer Fabricated by Chemical Molecular Beam Deposition for Use in Thin Film Solar Cells. Journal of Applied Physics, 112, Article ID: 023517.
http://dx.doi.org/10.1063/1.4739277 - 9. Guo, Y., Liu, X.L., Ping, S.H., Li, Y., Lin, Z.G., Yuan, W.H., Yan, Y.S., Sheng, Z.Q. and Guo, W.Z. (2010) Measurement of GaN/Ge(001) Heterojunction Valence Band Offset by X-Ray Photoelectron Spectroscopy. Chinese Physics Letters, 27, Article ID: 067302.
http://dx.doi.org/10.1088/0256-307X/27/6/067302 - 10. Adachi, S., Kimura, T. and Suzuki, N. (1993) Optical Properties of CdTe: Experiment and Modelling. Journal of Applied Physics, 74, 3435-3441.
http://dx.doi.org/10.1063/1.354543 - 11. Niasse, O.A., Mbengue, B., B. BA and Youm, I. (2010) Models Calculation of Absorption Coefficient of the Theory of Solar Cell n-CdS/p-CdTe. Renewable Energy Journal, 12, No. 3.
http://www.cder.dz/ - 12. Salavei, A., Rimmaudo, I., Piccinelli, F. and Romeo, A. (2013) Influence of CdTe Thickness on Structural and Electrical Properties of CdTe/CdS Solar Cells. Thin Solid Films, 535, 257-260.
http://dx.doi.org/10.1016/j.tsf.2012.11.121 - 13. Gokmen, N., Karatepe, E., Ugranli, F. and Silvestre, S. (2013) Voltage Band Based Global MPPT Controller for Photovoltaic Systems. Solar Energy, 98, 322-334.
http://dx.doi.org/10.1016/j.solener.2013.09.025 - 14. Lalili, D., Mellit, A., Lourci, N., Medjahed, B. and Boubakir, C. (2013) State Feedback Control and Variable Step Size MPPT Algorithm of Three-Level Grid-Connected Photovoltaic Inverter. Solar Energy, 98, 561-571.
http://dx.doi.org/10.1016/j.solener.2013.10.024 - 15. Terrazas, J., Rodriguez, A., Lopez, C., Escobedo, A., Kuhlmann, F.J., McClure, J. and Zubia, D. (2005) Ordered Polycrystalline Thin Films for High Performance CdTe/CdS Solar Cells. Thin Solid Films, 490, 146-153.
http://dx.doi.org/10.1016/j.tsf.2005.04.047
NOTES
*Corresponding author.















