World Journal of Condensed Matter Physics
Vol.04 No.04(2014), Article ID:51597,1 pages
10.4236/wjcmp.2014.44026
Superconductivity
Jens Cordelair
Birkenweg 2, Elmenhorst, Germany
Email: Jens.Cordelair@freenet.de
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 19 September 2014; revised 20 October 2014; accepted 31 October 2014
ABSTRACT
The feature of quantum entanglement is used to create a new model for the superconducting state.
Keywords:
Quantum entanglement, superconductivity

1. Introduction
Unlike normal conductors such as copper or steel, a superconductor can carry an electric current for a very long time without relaxation. In 1911 when Heike Kammerlingh Onnes reached temperatures as low as 1.7 kelvin (K), one was able to induce a superconducting phase for the first time. Theoretical understanding of superconductivity was advanced in 1957 by the American physicists John Bardeen, Leon Cooper, and John Schrieffer. Their Theory of Superconductivity became known as the BCS theory [1] . However, the BCS theory must be inadequate to fully explain how superconductivity works, because it doesn’t take the quantum entanglement of the electronic system into account.
2. The C-model [2] with double quantum entanglement
According to the C-model the phenomenon of superconductivity can be consistently explained in therms of double entangled electrons. Simple spin-entanglement result in Cooper-pairs and the boson-gas of Cooper-pairs condensate into the entangled BCS ground state.
In the conventional quantum mechanics all matter-waves Ψ, describing a particle or a quantum mechanical system, are elements of a Hilbert-space. If we take entanglement into account this fundamental assumption is no longer valid. Bearing this inconvenience in mind a measurement of the energy by the Hamilton operator H can no longer be an eigenvalue equation (Schrödinger-equation) but can be written as
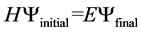 (1)
(1)
where Ψ is not an element of a Hilbert-space (the space is not separable).
We denote the spectrum and its characteristic vectors of the Hamilton operator of a system of electrons in the conventional quantum mechanics as band structure. Following this convention we may also designate the energy distribution of a system with entanglement as density of states part of the band structure.
The electrons in an atom are fragmented into paired wave-functions (orbitals) of constant energy but antipodal spin (entangled spins), which induces a partly bosonic characteristic. This is why I would like to call these orbitals bound Cooper-pairs [3] . In a solid these orbitals are shared with neighboring atoms (directed binding e.g. ceramics) or more spread out (metallic binding).
At 0˚K the orbitals of all atoms in a flawless crystal are perfectly spin entangled and the width of an energy band is reduced to a single value (BEC ground state for this energy band). Due to energy entanglement the solid interact as a whole obeying the Mössbauer-effect. In accordance with the classical aggregate states gaseous, liquid and solid I would like to name this state the coherent state. The discreteness of the density of states part of the band structure allow no change of state of the electronic system, thus a once incited current can't relax and persist for a very long time. The material is in the superconducting state.
Increasing the temperature result in distortions of the lattice and part of the orbitals lose their entanglement (bosonic characteristic) due to thermal chaos, where only the overall spin stays the same. The body gets split into coherent and solid phases. Below a critical temperature Tc the coherent phases are interconnected, forming a percolating superconducting backbone. Above Tc the density of the coherent phases is to low to form up a percolating backbone and the body is in the normal conducting state.
3. Conclusion
It has been shown that the decoupling of the novel C-model from the particulate structure of electrons in matter gives a new understanding for the mechanisms leading to superconductivity. The transition of the electronic system from a fermion characteristic to a boson characteristic incites the formation of a Bose-Einstein-Con- densate which exhibits the capacity of superconductivity. In the future this novel comprehension of how superconductivity works may give a guideline to develop improved superconductors especially in the high-tempera- ture superconductivity area.
References
- Bardeen, J., Cooper, L.N. and Schriffer, J.R. (1957) Microscopic Theory of Superconductivity. Physical Review, 106, 162-164.
- Cordelair J. (2013) Double Quantum Entanglement to Understand Superconductivity. World Journal of Condensed Matter Physics, 3, 194-197. http://dx.doi.org/10.4236/wjcmp.2013.34032
- Cooper, L.N. (1956) Bound Electron Pairs in a Degenerate Fermi Gas. Physical Review, 104, 1189-1190. http://dx.doi.org/10.1103/PhysRev.104.1189

