World Journal of Condensed Matter Physics
Vol.3 No.3(2013), Article ID:35819,8 pages DOI:10.4236/wjcmp.2013.33023
Energy Structure of Two-Dimensional Graphene-Semiconductor Quantum Dot
![]()
1Department of Physics, Southern University and A&M College, Baton Rouge, USA; 2Xiamen University, Xiamen, China; 3Institute of Mechanics, Chinese Academy of Sciences, Beijing, China.
Email: wangjintong@gmail.com
Copyright © 2013 Jin Tong Wang et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received May 7th, 2013; revised June 21st, 2013; accepted July 5th, 2013
Keywords: Graphene; Quantum Dot; Dirac Equation; Semiconductor; Energy Levels
ABSTRACT
Graphene is a newly discovered material that possesses unique electronic properties. It is a two-dimensional singlelayered sheet in which the electrons are free and quasi-relativistic. These properties may open a door for many new electronic applications. In this paper we proposed a flat 2-dimensional circular graphene-semiconductor quantum dot. We have carried out theoretical studies including deriving the Dirac equation for the electrons inside the graphenesemiconductor quantum dot and solving the equation. We have established the energy structure as a function of the rotational quantum number and the size (radius) of the dot. The energy gap between the energy levels can be tuned with the radius of the quantum dot. It could be useful for quantum computation and single electron device application.
1. Introduction
Traditionally, quantum dots are nano-particles of a semiconductor material, such as chalcogenides of metals like cadmium or zinc, for example CdSe or ZnS. The size of the particles ranges from 2 to 10 nanometers in diameter [1]. Excitons, such as electrons or holes in a quantum dot are confined in all three spatial dimensions. Therefore, the electronic properties in quantum dot lay intermediate amid those of bulk materials and those of discrete atoms or molecules [1-4]. They were discovered at the beginning of the 1980s by Alexei Ekimov [1,5]. Graphene, a new class of two-dimensional (2D) carbon material with single-atom-thick layer features different from ball-like C60 and one-dimensional carbon nanotubes, has attracted attention in recent years [6-10]. Single atom layer graphene possesses unique electric properties. The energy bands of graphene can be described by a two-dimensional Dirac equation centered on hexagonal corners (Dirac points) of the honeycomb lattice Brillouin zone [11-13]. Particularly, the low energy band structure of graphene is gapless and the corresponding electronic states are found near two cones located at unequivalent corners of the Brillouin zone [12-14]. The low-energy carrier dynamics ![]() is equivalent to that of a 2D gas of massless charged fermions [12,15,16]. Many studies of electronic properties, transport properties of a nanoscale graphene strips were performed over the past years [14,17-24]. Transistors using graphene strip and graphene quantum dot have be fabricated recently [25,26]. Quantum dot may have applications in quantum computer and single-electron device.
is equivalent to that of a 2D gas of massless charged fermions [12,15,16]. Many studies of electronic properties, transport properties of a nanoscale graphene strips were performed over the past years [14,17-24]. Transistors using graphene strip and graphene quantum dot have be fabricated recently [25,26]. Quantum dot may have applications in quantum computer and single-electron device.
The layered graphene quantum dot mentioned above which has two different boundary conditions corresponding to two types of graphene edges, i.e., the zigzag and “armchair” [20,27], currently attracts intensively investigations world-wide [12,19].
In this paper we proposed a novel type of quantum dot, single layered two-dimensional (flat) graphene quantum dot composed of a small (in nanometer) circular graphene layer surrounded by a large gap semiconductor layer on a insulating substrate and carried out a theoretical study of such quantum dot. The Dirac equation in polar coordinate was derived and solved by variableseparation and series method. The energy structure of such quantum dot is found to have two discrete states and depends on the rotational quantum number and the size (radius) of the dot.
2. Electron Wave Functions in Graphene-Semiconductor Quantum Dot
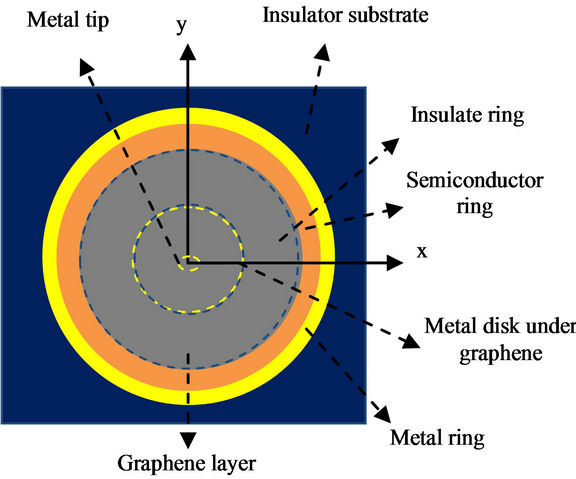
The structure of the graphene-semiconductor quantum dot is shown in Figure 1. Electrons in graphene can be
 (a)
(a) (b)
(b)
Figure 1. Structure of the graphene quantum dot. (a) Top view; (b) side view.
treated as massless particles. Their behavior is governed by Dirac Hamiltonian [12,15,16]..
The Hamiltonian including the energy gaps of the semiconductor film surrounding the graphene circular dot and a diagonal effective mass-like term ![]() is [12]
is [12]
 and the Dirac equation is
and the Dirac equation is
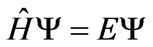 (1)
(1)
and
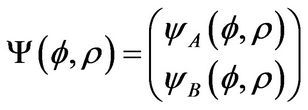 (2)[12]
(2)[12]
where 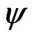 is the wave function as a function of
is the wave function as a function of ![]() which are polar coordinates, angle and radius respectively.
which are polar coordinates, angle and radius respectively.
Since the effective mass of electrons in graphene sheet near the corners of the Brillouin zone is close to massless, the Hamiltonian of the electrons is nearly relativistic. Hence, the energy of the electrons in the graphene sheet mostly arises from the spin-orbit interaction [12,28]. In polar coordinates, the momentum operator can be written as
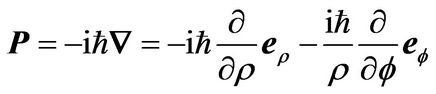 (3)
(3)
The Pauli vector is
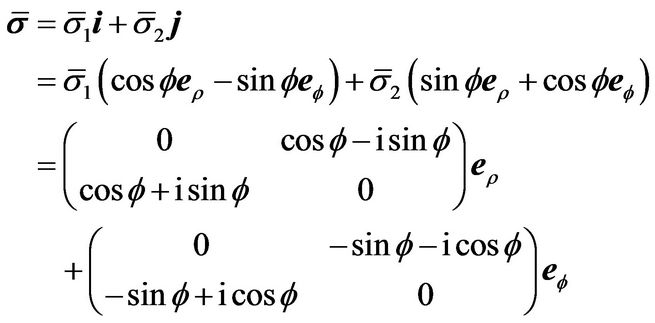 (4)
(4)
Combining Equations (3) and (4), we obtain
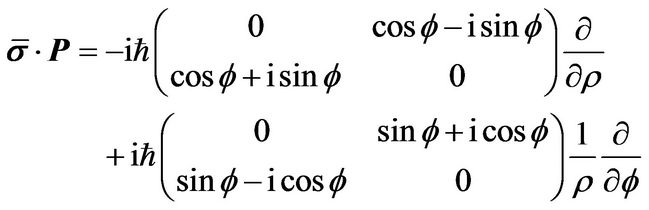
The Hamiltonian

The Dirac Equation (1) then becomes
 (5)
(5)
Equation (5) consists of two equations. These are:
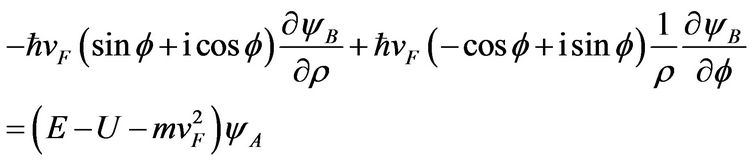 (6)
(6)
and
 (7)
(7)
Letting

and

where
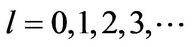 .
.
Substituting these two functions into Equations (6) and (7), we obtain the following two equations:
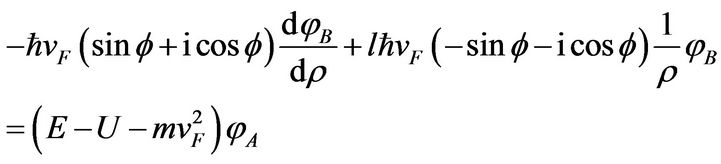 (8)
(8)
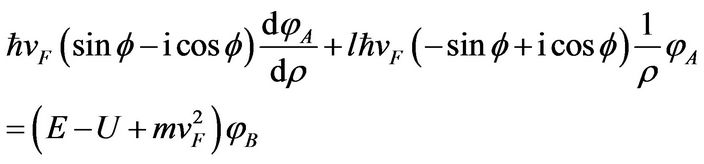 (9)
(9)
Differentiating Equation (8), one finds
 (10)
(10)
From Equation (9), one can find
 (11)
(11)
Substituting Equation (11) into Equation (10), we find
 (12)
(12)
From Equation (8), we also find
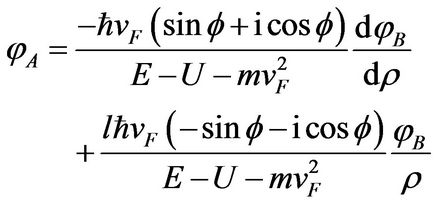 (13)
(13)
Substituting Equation (13) into Equation (12), Equation (12) becomes
 (14)
(14)
After some cancelations, Equation (14) becomes
 (14)’
(14)’
For inside the graphene quantum dot,  , the potential energy U = 0. And
, the potential energy U = 0. And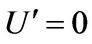 . Therefore, Equation (14) becomes
. Therefore, Equation (14) becomes
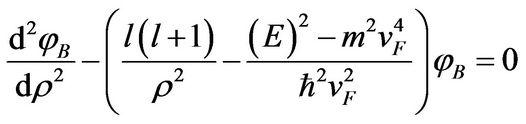 (14)”
(14)”
Letting , and
, and , Equation (14)” then becomes
, Equation (14)” then becomes
 (15)
(15)
where
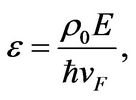 and
and 
For , i.e.
, i.e. , outside the dot, electrons are no longer in graphene layer. Instead, electrons are in semiconductor which should be described by Schrodinger equation. We will study this case in other paper. In this paper, we only deal with the case that the energy gap of the semiconductor is infinite. The potential function can be expressed as
, outside the dot, electrons are no longer in graphene layer. Instead, electrons are in semiconductor which should be described by Schrodinger equation. We will study this case in other paper. In this paper, we only deal with the case that the energy gap of the semiconductor is infinite. The potential function can be expressed as
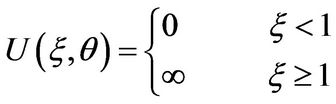
3. Wave Function and Energy States of the Electrons inside the Dot
To find the wave functions and the energy states of the electrons inside the quantum dot, we have to first solve Equation (15). Equation (15) is an eigen value-eigen function equation. From this equation, one can see that the eigen values  can be positive or negative. Since the value for
can be positive or negative. Since the value for ![]() is usually very small. Hence let us first consider
is usually very small. Hence let us first consider  is positive.
is positive.
Letting
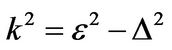
assuming
 then
then
 and
and
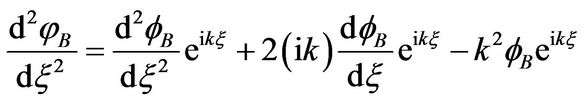
Substituting the above function and their derivatives into Equation (15), we find the equation of 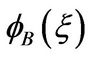
 (16)
(16)
assuming
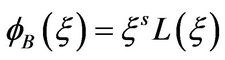 then
then
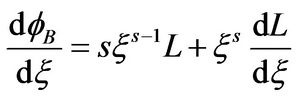
and

Substituting the above two equations into Equation (16), we obtain the following equation
 (17)
(17)
Letting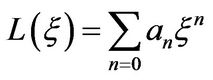 , and substituting this series into Equation (17), we obtain the following equation
, and substituting this series into Equation (17), we obtain the following equation
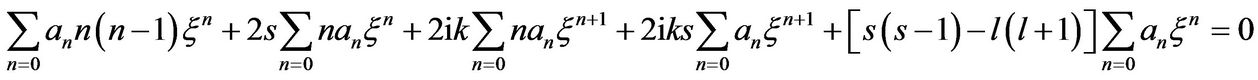 (18)
(18)
From Equation (18), we determine the recursion relation of the series coefficients.
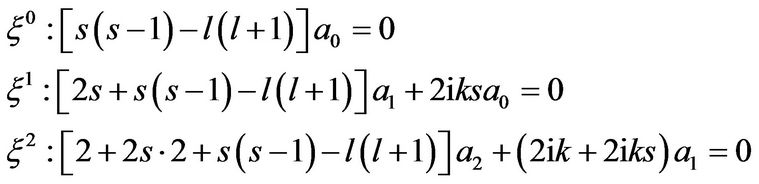 (19)
(19)
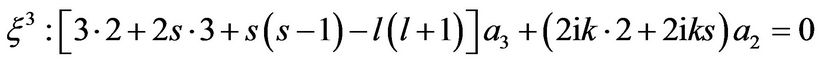 (20)
(20)

![]() (21)
(21)
The recursion relation may be extrapolated as
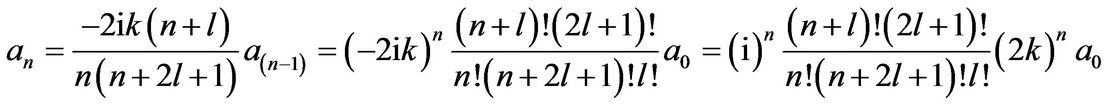 (22)
(22)
For no trivial solution,  , then
, then 
Finally,
 (23)
(23)
The general solution  can be formed as
can be formed as
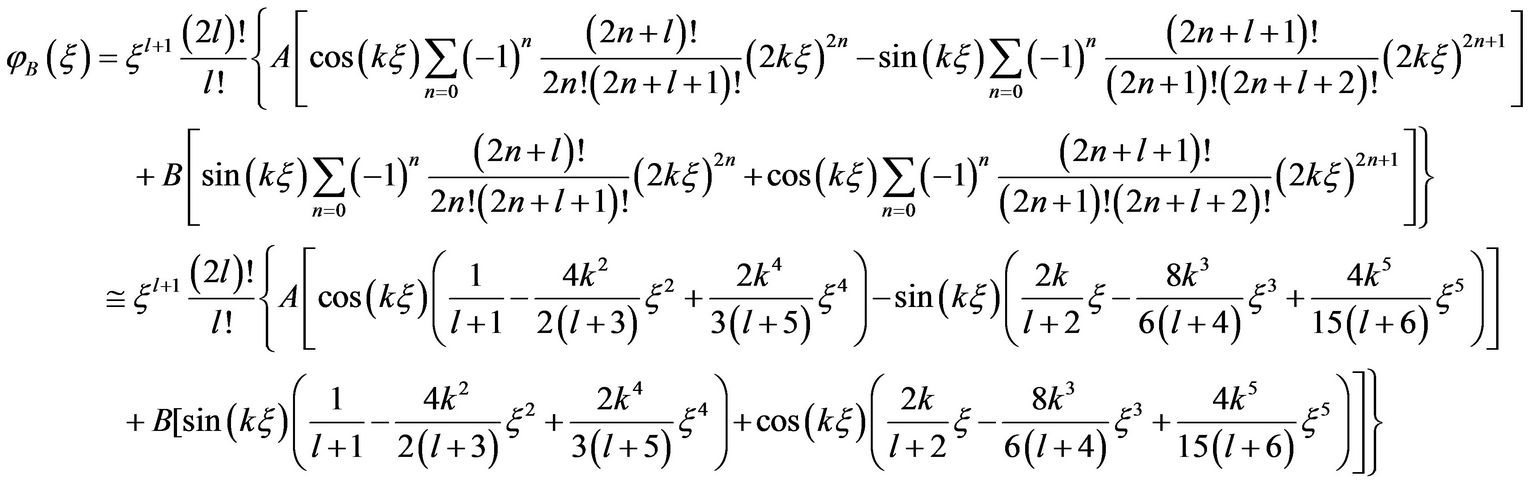 (24)
(24)
One can note that the series above converges fast. Therefore, we make the third order-approximation. The B-component of the wave function then can approximately be obtained as
 (25)
(25)
With Equation (13), one can find the A-component of the wave function.
when , the boundary conditions are:
, the boundary conditions are:
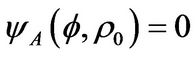
or
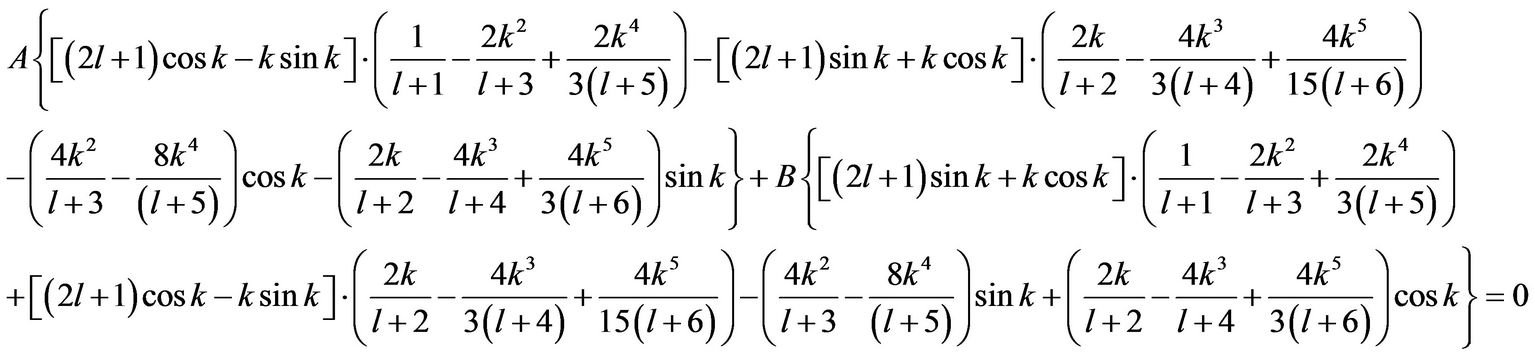 (26)
(26)
and
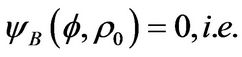

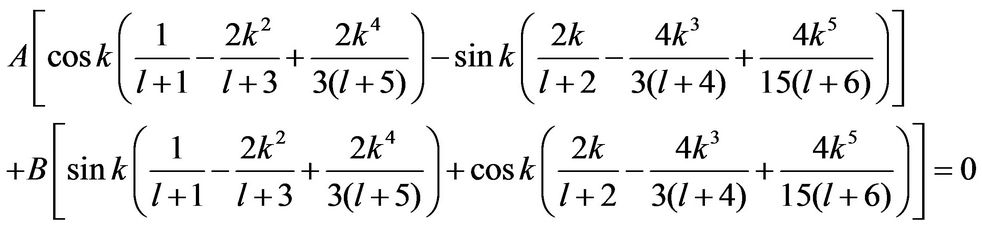 (27)
(27)
From Equations (26) and (27), one can conclude that only the value of the determinant of coefficients A and B in Equations (26) and (27) equals to rezo, i.e..
 (28)
(28)
then the wave functions  have nonzero solutions. And the above equation determines the values of k and then the energy level E. The above equation was numerically solved. And we found the solutions of k as a function of l which are plotted in Figure 2. Then the energy level
have nonzero solutions. And the above equation determines the values of k and then the energy level E. The above equation was numerically solved. And we found the solutions of k as a function of l which are plotted in Figure 2. Then the energy level
 (29)
(29)
Tipically
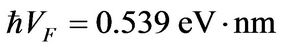 [12]
[12]
and
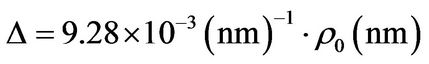 [12]then
[12]then
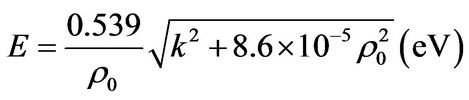
This relation for l = 0 is plotted in Figure 3.
4. Conclusion
We have derived and solved the Dirac equation for a flat circular graphene-semiconductor quantum dot. The series method was employed and the recursion relation of the coefficients of the series was found. The wave function 
 was approximately established. The energy related quantum number k were obtained as a function of rotation quantum number l. one can see that for each l there are two values of k. Namely, there are two energy levels. The smaller value of k, i.e. the first energy level increases slightly with l when l < 1. After l > 1, k is approximately a constant. The higher k, i.e. the higher energy level decreases slightly with increasing l and as-
was approximately established. The energy related quantum number k were obtained as a function of rotation quantum number l. one can see that for each l there are two values of k. Namely, there are two energy levels. The smaller value of k, i.e. the first energy level increases slightly with l when l < 1. After l > 1, k is approximately a constant. The higher k, i.e. the higher energy level decreases slightly with increasing l and as-

Figure 2. Quantum number k versus quantum number l.

Figure 3. Energy levels versus the size of the dot for l = 0.
ymptotically approaches a constant. These two states of the electrons in such graphene quantum dot are clear and stable. From Figure 3 we can see that the energy levels E of the quantum dot decrease with the increasing size of the quantum dot . Therefore, the energy gap between these two energy levels may be tuned with the radius of the quantum dot. It may have potential applications in quantum computation and developing a single-electron device.
. Therefore, the energy gap between these two energy levels may be tuned with the radius of the quantum dot. It may have potential applications in quantum computation and developing a single-electron device.
Acknowledgements
The work is partially supported by Air Force Office of Scientific Research (Award No. FA9550-09-1-0367) and the National Science Foundation (Award No. CBET- 0754821) and the National Science Foundation (NSF) and the Louisiana Board of Regents, through LASiGMA [Award Nos. EPS- 1003897, NSF (2010-15)-RII-SUBR].
REFERENCES
- “Quantum Dots—Background Briefing”. http://www.nanocotechnologies.com
- L. E. Brus, “Chemistry and Physics of Semiconductor Nanocrystals,” 2007. http://www.columbia.edu/cu/chemistry/fac-bios/brus/group/pdf files/semi_nano_website_2007.pdf
- D. J. Norris, “Measurement and Assignment of the SizeDependent Optical Spectrum in Cadmium Selenide (CdSe) Quantum Dots,” Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, 1995.
- C. B. Murray, C. R. Kagan and M. G. Bawendi, “Synthesis and Characterization of Monodisperse Nanocrystals and Close-Packed Nanocrystal Assemblies,” Annual Review of Materials Research, Vol. 30, No. 1, 2000, pp. 545-610.
- A. I. Ekimov and A. A. Onushchenko, “Quantum Size Effect in Three-Dimensional Microscopic Semiconductor Crystals,” Jounal of Experimental and Theoretical Physics Letters, Vol. 34, 1981, pp. 345-349.
- C. X. Guo, H. B. Yang, Z. M. Sheng, Z. S. Lu, Q. L. Song and C. M. Li, “Layered Graphene/Quantum Dots for Photovoltaic Devices,” Angewandte Chemie International Edition, Vol. 49, No. 17, 2010, pp. 3014-3017.
- W. X. Zhang, J. C. Cui, C. A. Tao, Y. G. Wu, Z. P. Li, L. Ma, Y. Q. Wen and G. T. Li, “A Strategy for Producing Pure Single-Layer Graphene Sheets Based on a Confined Self-Assembly Approach,” Angewandte Chemie International Edition, Vol. 48, No. 32, 2009, pp. 5864-5868. doi:10.1002/anie.200902365
- D. Li, M. B. Muller, S. Gilje, R. B. Kaner and G. G. Wallace, “Processable Aqueous Dispersions of Graphene Nanosheets,” Nature Nanotechnology, Vol. 3, 2008, pp. 101-105. doi:10.1038/nnano.2007.451
- X. Wang, L. J. Zhi, N. Tsao, Z. Tomovic, J. L. Li and K. Mullen, “Transparent Carbon Films as Electrodes in Organic Solar Cells,” Angewandte Chemie International Edition, Vol. 47, No. 16, 2008, pp. 2990-2992. doi:10.1002/anie.200704909
- X. Wang, L. J. Zhi and K. Mullen, “Transparent, Conductive Graphene Electrodes for Dye-Sensitized Solar Cells,” Nano Letters, Vol. 8, No. 1, 2008, pp. 323-327. doi:10.1021/nl072838r
- L. P. An, T. B. Wang and N. H. Liu, “Inter-Well Coupling and Resonant Tunneling Modes of Multiple Graphene Quantum Wells,” Communications in Theoretical Physics, Vol. 56, No. 2, 2011, pp. 367-372. doi:10.1088/0253-6102/56/2/29
- J. M. Pereira Jr., V. Mlinar and F. M. Peeters, “Confined States and Direction-Dependent Transmission in Graphene Quantum Wells,” 2006.
- P. R. Wallace, “The Band Theory of Graphite,” Physical Review, Vol. 71, No. 9, 1947, pp. 622-634. doi:10.1103/PhysRev.71.622
- M. Wilson, “Electrons in Atomically Thin Carbon Sheets Behave Like Massless Particles,” Physics Today, Vol. 59, No. 1, 2006, p. 21. doi:10.1063/1.2180163
- G. W. Semenoff, “Condensed-Matter Simulation of a Three-Dimensional Anomaly,” Physical Review Letters, Vol. 53, No. 26, 1984, pp. 2449-2452. doi:10.1103/PhysRevLett.53.2449
- I. A. Luk’yanchuk and Y. Kopelevich, “Phase Analysis of Quantum Oscillations in Graphite,” Physical Review Letters, Vol. 93, No. 16, 2004, Article ID: 166402. doi:10.1103/PhysRevLett.93.166402
- L. A. ponomarenko, F. Schedin, M. I. Katsnelson, R. Yang, E. W. Hill, K. S. Novoselov and A. K. Geim, “Chaotic Dirac Billiard in Graphene Quantum Dots,” Science, Vol. 320, No. 5874, 2008, pp. 356-358.
- T. Ando, “Theory of Electronic States and Transport in Carbon Nanotubes,” Journal of Physical Society of Japan, Vol. 74, No. 3, 2005, pp. 777-817. doi:10.1143/JPSJ.74.777
- P. V. Ratnikov and A. P. Silin, “Quantum Well Based on Graphene and narrow-Gap Semiconductors,” Bulletin of the Lebedev Physics Institute, Vol. 36, No. 2, 2009, pp. 34-43. doi:10.3103/S106833560902002X
- K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, M. I. Katsnelson, I. V. Grigorieva, S. V. Dubonos and A. A. Firsov, “Two-Dimensional Gas of Massless Dirac Fermions in Graphene,” Nature, Vol. 438, No. 7065, 2005, pp. 197-200. doi:10.1038/nature04233
- Y. Zhang, Y.-W. Tan, H. L. Stormer and P. Kim, “Experimental Observation of the Quantum Hall Effect and Berry’s Phase in Graphene,” Nature, Vol. 438, No. 7065, 2005, pp. 201-204. doi:10.1038/nature04235
- L. Brey and H. A. Fertig, “Electronic States of Graphene Nanoribbons,” Physical Review B, Vol. 73, No. 23, 2006, Article ID: 235411. doi:10.1103/PhysRevB.73.235411
- L. Brey and H. A. Fertig, “Elementary Electronic Excitations in Graphene Nanoribbons,” Physical Review B, Vol. 75, No. 12, 2007, Article ID: 125434. doi:10.1103/PhysRevB.75.125434
- Y.-W. Son, M.L. Cohen, S.G. Louie, “Energy Gaps in Graphene Nanoribbons,” Physical Review Letters, Vol. 97, No. 21, 2006, Article ID: 216803. doi:10.1103/PhysRevLett.97.216803
- E. Mccann and V. I. Fal’ko, “Symmetry of Boundary Conditions of the Dirac Equation for Electrons in Carbon Nanotubes,” Journal of Physics: Condensed Matter, Vol. 16, No. 13, 2004, pp. 2371-2379. doi:10.1088/0953-8984/16/13/016
- X. Wang, Y. Ouyang, X. Li, H. Wang, J. Guo and H. Dai, “Room-Temperature All-Semiconducting Sub-10-nm Graphene Nanoribbon Field-Effect Transistors,” Physical Review Letters, Vol. 100, No. 20, 2008, Article ID: 206803. doi:10.1103/PhysRevLett.100.206803
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, “Physical Properties of Carbon Nanotubes,” Imperial College Press, London, 1998. doi:10.1142/p080
- J. T. Wang, D. S. Guo, G. L Zhao, J. C. Chen, Z. W. Sun and A. Ignatiev, “Graphene-Semiconductor Quantum Well with Asymmetric Energy Gaps,” World Journal of Condensed Matter Physics, Vol. 3, No. 1, 2013, pp. 67-72. doi:10.4236/wjcmp.2013.31012

