World Journal of Condensed Matter Physics
Vol.2 No.3(2012), Article ID:22122,4 pages DOI:10.4236/wjcmp.2012.23021
Band Structure of AlSb Nanoclusters
![]()
Physics Department, College of Science, University of Babylon, Hilla, Iraq.
Email: abdullettif@yahoo.com
Received April 14th, 2012; revised May 15th, 2012; accepted May 23rd, 2012
Keywords: Nanocluster; Band Structure; AlSb
ABSTRACT
Ab initio restricted Hartree-Fock method within the framework of large unit cell formalism is used to investigate the band structure of AlSb nanoclusters. Large unit cells of 8, 16, 54, 64 and 128 atoms are used to analyze the cohesive energy, energy gap, valence bandwidth, and the density of states of the energy levels for AlSb nanoclusters. The results of the present work revealed that the band structure of AlSb nanoclusters differs significantly from that of the bulk AlSb crystal. Also, it is found that the valence band width and the cohesive energy (absolute value) increase as the AlSb crystal size increases, and they tend to stabilize for nanoclusters of more than 50 atoms.
1. Introduction
Aluminum antimonide (AlSb) is a compound semiconductor with an indirect band gap and has the zinc-blende (zb) structure [1]. AlSb crystal is used in a multitude of device applications, including light-emitting diodes (LEDs), lasers, detectors, and communication devices. It is also fabulous optical material, where it can be made to emit light efficiently, convert light energy into electrical energy, modulate the intensity of light and used as optical filters, mirrors, lenses, etc. [2].
In the present work we introduce the ab-initio restricted Hartree-Fock (RHF) formalism within the frame of large unit cell (LUC) method to investigate the band structure of AlSb nanoclusters. This method has been chosen in the present work rather than other methods because this method is very reliable to analyze the electronic properties of solids, and because of the significant advantage of ab initio methods which is the ability to study reactions that involve breaking or formation of covalent bonds, which correspond to multiple electronic states. The downside of ab initio methods is their computational cost. They often take enormous amounts of computer time, memory, and disk space [3].
Aluminum antimonide has been intensively investigated in the recent years, where Mohammad and Katircioglu [4] studied the electronic band structure of AlSb nanoclusters and they found that the indirect band gap of AlSb is close to its experimental value, but the direct band gap has a small discrepancy with its experimental value. De and Pryor [5] studied the electronic band structure of AlSb semiconductor in WZ phase and they showed that AlSb crystal has smaller direct gaps than their indirect gaps in ZB phase. The aim of the present work is to investigate the band structure of AlSb nanoclusters using Hartree-fock formalism within the frame of large unit cell employing Gaussian 03 program (computer software is capable of predicting many properties of molecules and reactions, including the molecular energies and structures) [6] to perform the calculations.
2. Theory
The main idea of the large unit cell is computing the electronic structure of the unit cell extended in a special manner at k = 0 in the reduced Brillouin zone [7]. Using the linear combination of atomic orbitals (LCAO) (approximation of the molecular orbital function as a linear combination of atomic orbitals chosen as the basis functions), the crystal wavefunction (ψi) in the (LUC-RHF) formalism is written in the following form [8]:
 (1)
(1)
where ψi is the molecular orbital, Cμi are the molecular orbital expansion coefficients, 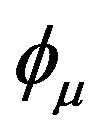 is the atomic orbital, N0 is the number of the atomic orbitals. The total electronic energy can be written as [9]:
is the atomic orbital, N0 is the number of the atomic orbitals. The total electronic energy can be written as [9]:
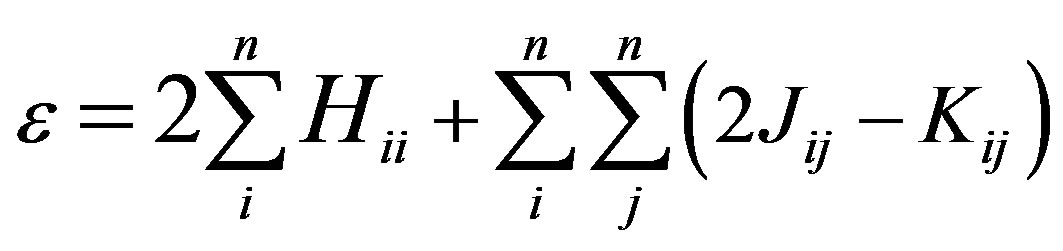 (2)
(2)
where Hii is the expectation value of the one electron core Hamiltonian corresponding to the molecular orbital ( ), Jij and Kij are the Coulomb and exchange operators respectively, and they are expressed as follows :
), Jij and Kij are the Coulomb and exchange operators respectively, and they are expressed as follows :
 (3)
(3)
 (4)
(4)
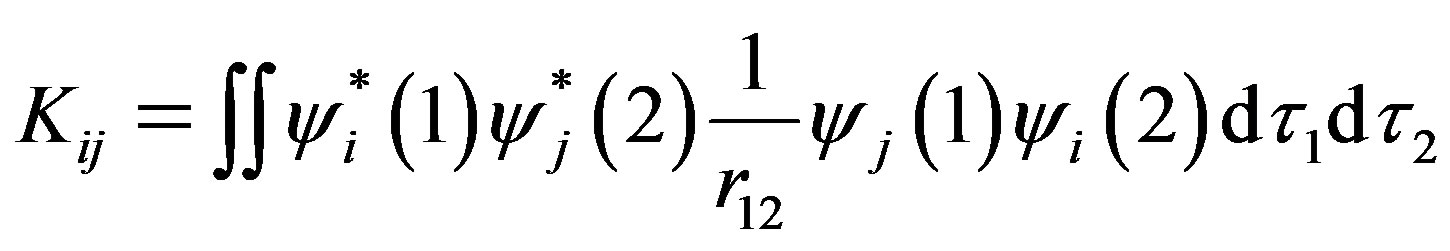 (5)
(5)
Substituting the linear expansion of Equation (1) in the molecular orbital integrals, yields:
 (6)
(6)
where 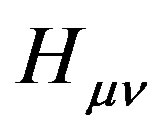 is the core Hamiltonian matrix elements,
is the core Hamiltonian matrix elements,
 (7)
(7)
 (8)
(8)
 (9)
(9)
where 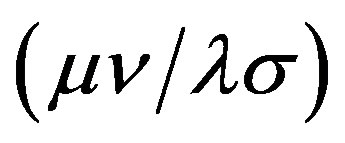 is the differential overlap matrix elements,
is the differential overlap matrix elements,
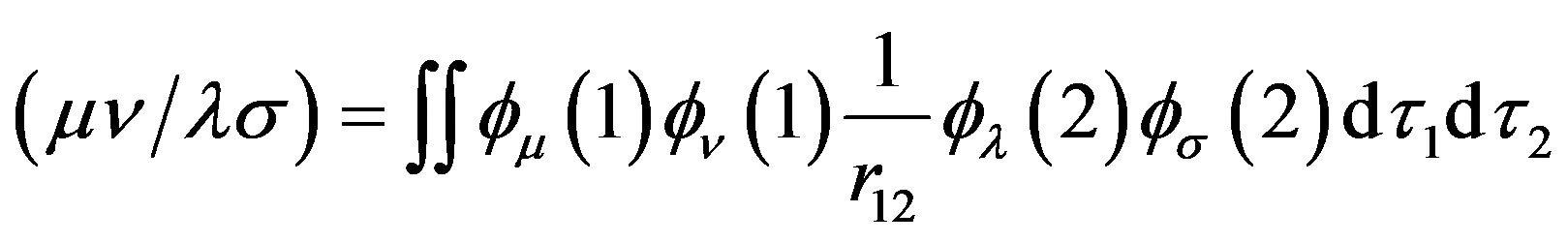 (10)
(10)
The total electronic energy of Equation (2) can be written in terms of integral over atomic orbitals. By substituting the previous expressions in the equation of the electronic energy, we obtain
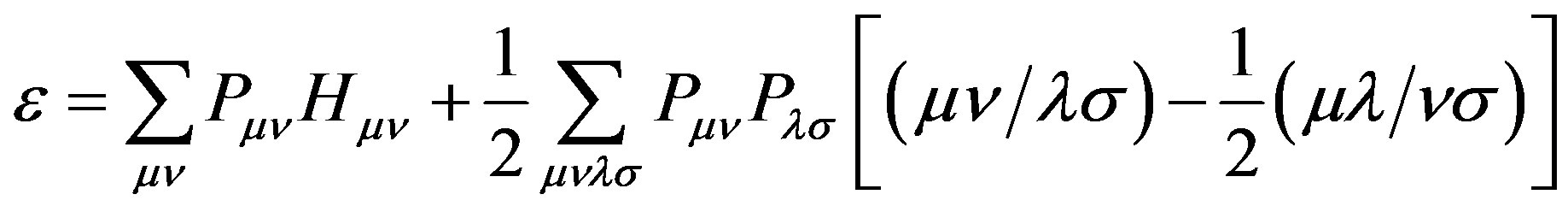 (11)
(11)
where  is the density matrix elements,
is the density matrix elements,
 (12)
(12)
The summation is over occupied orbitals only for closed shell systems which is the case in the present work. Applying the variational method to Equation (11), a small variation of the molecular orbital  can now be given as:
can now be given as:
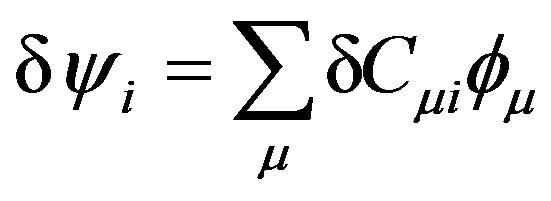 (13)
(13)
And when applying the condition for a stationary point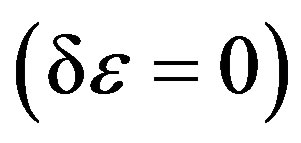 , one can obtain the following final form [10,11],
, one can obtain the following final form [10,11],
 (14)
(14)
where 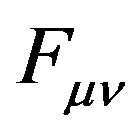 is the Fock matrix,
is the Fock matrix,
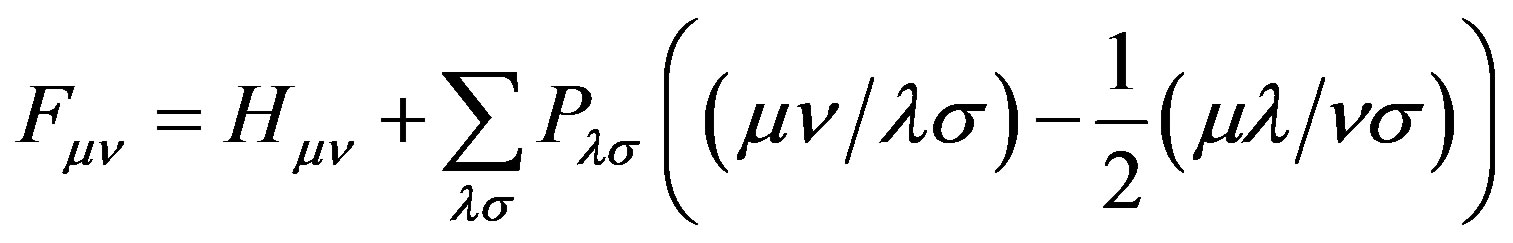 (15)
(15)
3. Results and Discussion
In the present work, we have used Gaussian program to calculate the lattice constant, energy gap, cohesive energy, valence band width and degeneracy of states of AlSb nanoclusters. These properties are illustrated in Table 1 and compared with other experimental and theoretical results. In the present work, we chose the number of atoms (8, 16, 54, 64 and 128) for the (LUC). The calculated total energy of AlSb crystal as a function of lattice constant for the LUC of (8) atoms is shown in Figure 1. The equilibrium lattice constant is deduced from the minimum of the total energy curve.
From Figure 1, it is shown that the total energy decreases with increasing the lattice constant till it reaches the equilibrium lattice constant. After the equilibrium lattice constant, the total energy increases with increasing lattice constant. The behavior of the total energy as a function of lattice constant is due to the attraction forces that take place at the large distances between atoms. Decreasing the distance between atoms leads to decrease the total energy. At shorter distances between atoms, the repulsion forces become dominant and take place to cause the increase of the total energy. The stability of the crystal at the equilibrium lattice constant is due to the equality of attraction and repulsion forces at this point. In the present work, we can see that the cohesive energy increases with increasing the number of atoms per LUC,
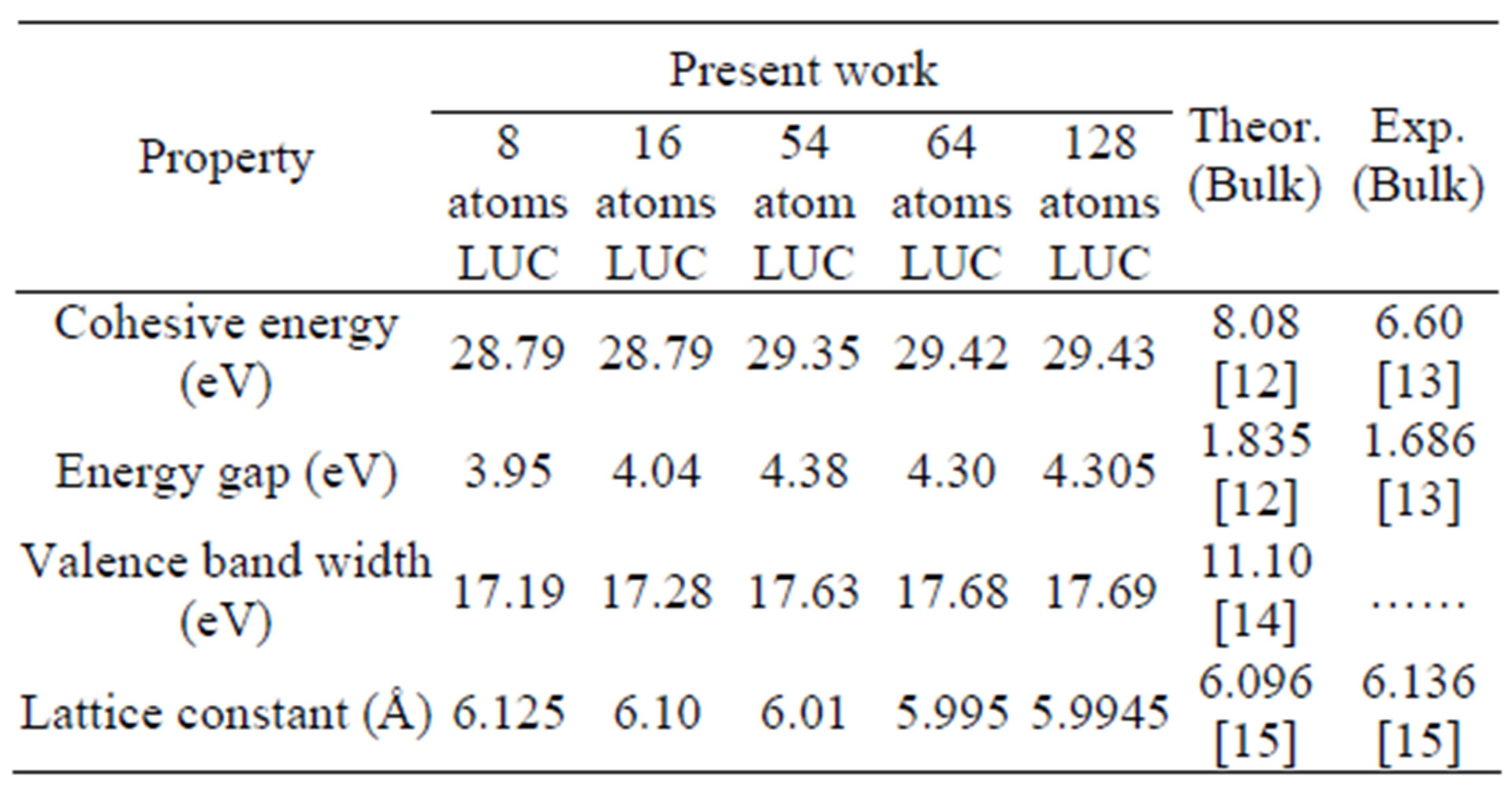
Table 1. The electronic structure of AlSb nanoclusters.

Figure 1. Total energy as a function of lattice constant for 8 atoms nanocluster.
then it tends to stabilize for nanoclusters of more than 50 atoms as in Figure 2. The same behavior is also shown for the valence band width as in Figure 3. But we show that the energy gap has fluctuating values, these fluctuations are related to the geometry of the crystal.
An interesting observation is shown that the electronic structure of AlSb nanoclusters differs significantly from that of the bulk AlSb crystal. The cohesive energy of AlSb nanoclusters has high value in comparison with the experimental and theoretical values. Simple STO-3G basis is used in the present work to be able to reach higher number of atoms. The present value of the cohesive energy and other properties can be greatly enhanced by changing the simple STO-3G basis used in the present calculations to more sophisticated basis states. However, more sophisticated basis states consume more memory and computer time and will eventually prevent us from reaching a large number of atoms. The high value of the band gap can be attributed to the approximations involved in HF method as well as in the present RHF-LUC formalism.
The density of states in semiconductors is an important concept that expresses the number of states per unit volume and per unit energy. Density of states for (8, 128) atoms nanoclusters as a function of energy levels is shown in Figures 4 and 5 respectively.
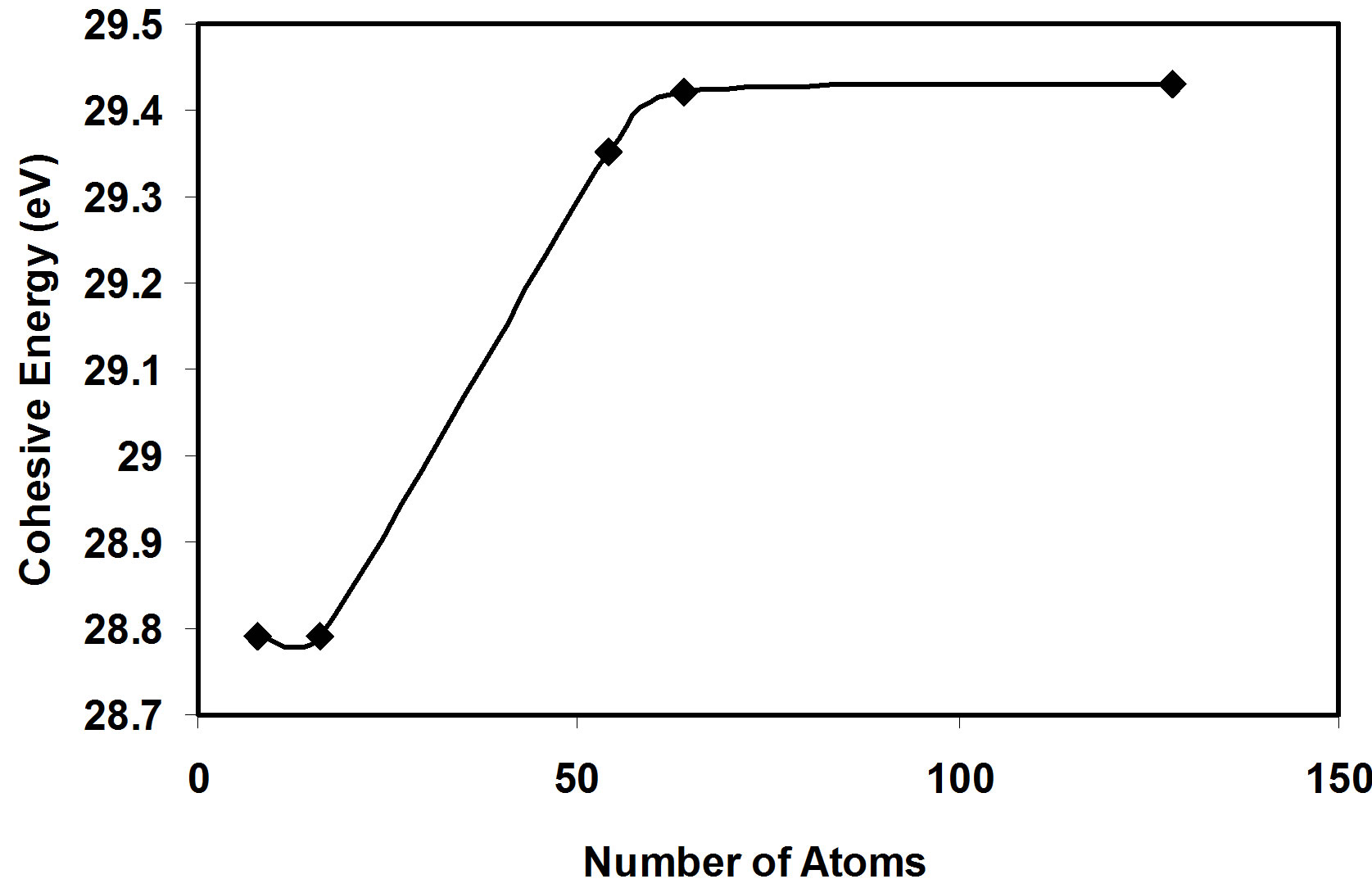
Figure 2. Cohesive energy as a function of number of atoms of AlSb nanoclusters.
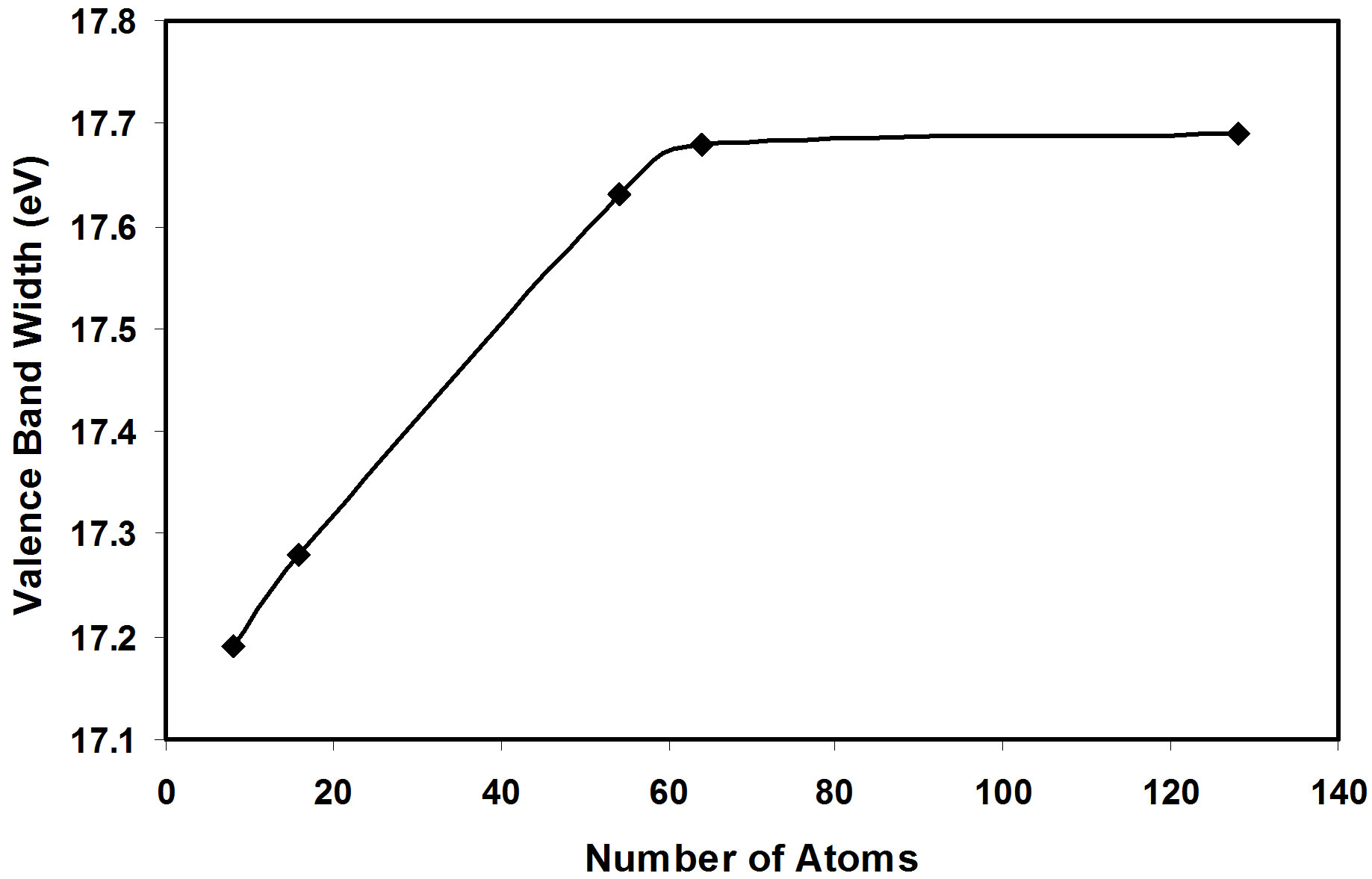
Figure 3. The valence band width as a function of number of atoms of AlSb nanoclusters.
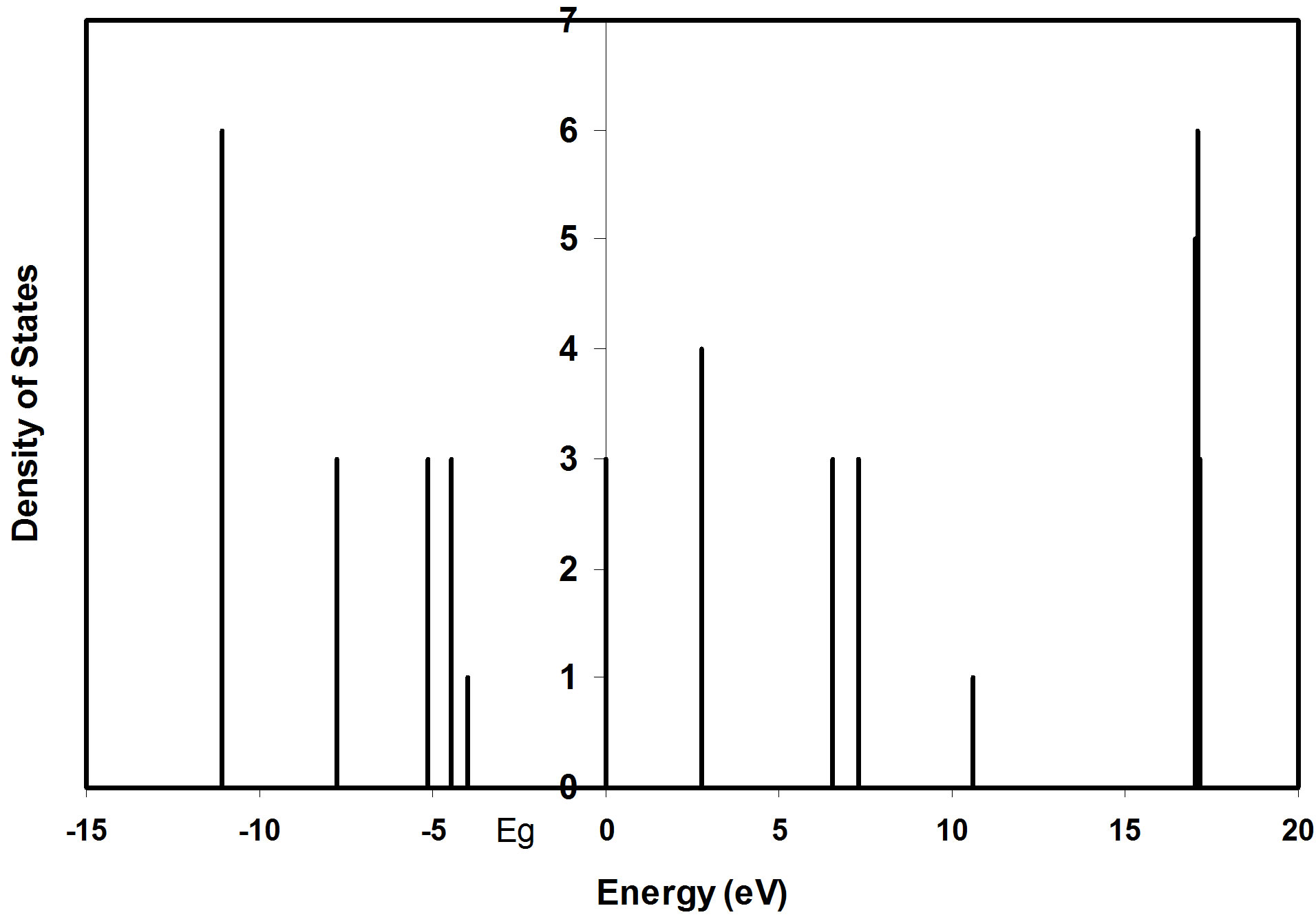
Figure 4. Density of states as a function of energy levels of 8 atoms nanocluster.
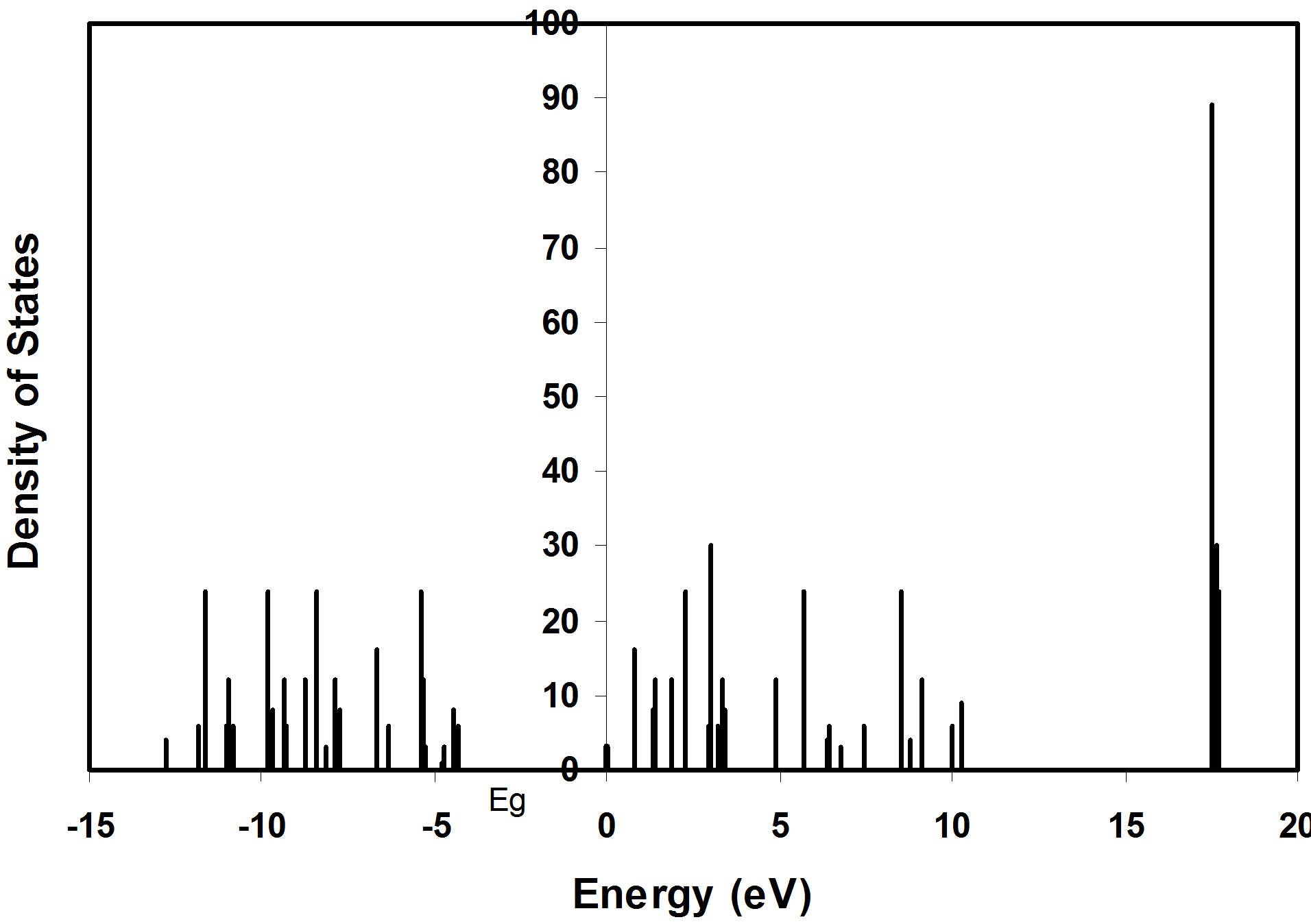
Figure 5. Density of states as a function of energy levels of 128 atoms nanocluster.
4. Conclusions
1) The present work reveals that the band structure of AlSb nanoclusters differs significantly from that of the bulk AlSb crystal.
2) The lattice constant of all size of AlSb crystal decreases with increasing the number of atoms in the LUC.
3) The present calculations show that the valence band width and the cohesive energy (absolute value) increases as the AlSb crystal size increases, and they tend to stabilize for nanoclusters of more than 50 atoms.
REFERENCES
- M. Grundmann, “The Physics of Semiconductors,” 2nd Edition, Springer-Verlag, Heidelberg, 2010. doi:10.1007/978-3-642-13884-3
- D. Aberg, P. Erhart, A. J. Williamson and V. Lordi, “Intrinsic Point Defects in Aluminum Antimonide,” Physical Review B, Vol. 77, No. 16, 2008, pp. 165206-165216.
- W. J. Hehre, L. Random, P. von R. Schleyer and J. Pople, “Ab Initio Molecular Orbital Theory,” John Wiley and Sons, Ltd., Hoboken, 1986.
- R. Mohammad and S. Katircioğlu, “The Electronic Band Structure of AlN, AlSb, AlAs and Their Ternary Alloys within,” International Journal of Modern Physics B, Vol. 20, No. 22, 2006, pp. 3199-3221. doi:10.1142/S0217979206035394
- A. De and C. E. Pryor, “Predicted Band Structures of III-V Semiconductors in the Wurtzite Phase,” Department of Physics and Astronomy and Optical Science and Technology Center, University of Iowa, Iowa, 2009.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, et al., “Gaussian 03, Revision B.01,” Gaussian, Inc., Pittsburgh, 2003.
- A. H. Harker and F. P. Larkins, “A Large Unit Cell Semiempirical Molecular Orbital Approach to the Properties of Solids. I. General Theory,” Journal of Physics C: Solid State Physics, Vol. 12, No. 13, 1979, pp. 2487-2495.
- H. Dorsett and A. White, “Overview of Molecular Modelling and ab Initio Molecular Orbital Methods Suitable for Use with Energetic Materials,” DSTO Aeronautical and Maritime Research Laboratory, Salisbury, 2000.
- V. Magnasco, “Methods of Molecular Quantum Mechanics,” John Wiley & Sons, Ltd., Genoa, 2009. doi:10.1002/9780470684559
- M. A. Abdulsattar, “Size Effects of Semiempirical Large Unit Cell Method in Comparison with Nanoclusters Properties of Diamond-Structured Covalent Semiconductors,” Physica E: Low-Dimensional Systems and Nanostructures, Vol. 41, No. 9, 2009, pp. 1679-1688. doi:10.1016/j.physe.2009.06.003
- W. Demtröder, “Molecular Physics: Theoretical Principles and Experimental Methods,” Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, 2005. doi:10.1002/9783527618095
- R. Ahmed, Fazal-e-Aleem, S. J. Hashemifar, H. Rashid and H. Akbarzadeh, “Physical Properties of III-Antiminodes—A First Principles Study,” Communications in Theoretical Physics, Vol. 52, No. 3, 2009, pp. 527-533. doi:10.1088/0253-6102/52/3/28
- R. W. G. Wyckoff, “Crystal Structures,” 2nd Edition, R. E. Krieger, Malabar, 1986.
- R. Mohammad, “The Electronic Band Structure of III (In, Al, Ga)-V (N, As, Sb) Compounds and Ternary Alloys,” M.Sc. Thesis, Middle East Technical University, Çankaya, 2005.
- L. N. Nikitina, S. V. Obukhov and V. G. Tyuterev, “Ab Initio Calculation of the Deformation Potentials for Intervalley Phonon-Assisted Transition in АIIIВV Crystals with Sphalerite Structure,” Russian Physics Journal, Vol. 52, No. 7, 2009, pp. 742-748. doi:10.1007/s11182-009-9289-1

