World Journal of Condensed Matter Physics
Vol.2 No.1(2012), Article ID:17635,8 pages DOI:10.4236/wjcmp.2012.21003
Variation of the Structural Properties of IV Element Nano Clusters Due to Tensile Stress
![]()
1Basic Science Department, Veterinary Medicine College, University of Babylon, Hilla, Iraq; 2Physics Department, College of Science, University of Babylon, Hilla, Iraq.
Email: *abdullettif@yahoo.com
Received November 29th, 2011; revised December 25th, 2011; accepted December 30th, 2011
Keywords: IV Elements; Structural Properties; Pressure; Nano Materials
ABSTRACT
CNDO/2 method with 27 unit cells composed of 216 atoms, has been used for calculating and studying the lattice constant, density, total energy, cohesive energy, bulk modulus, microhardness, Young modulus, speed of sound, acoustic phonons energy, plasmon energy and vibrational energy, for diamond, silicon, germanium, and gray tin subjected to tensile stress. And to investigate the categories of these clusters; do these clusters have properties of nano materials or properties of bulk materials? It is found that most values of the investigated properties decrease with tensile stress except the lattice constant and the vibrational energy. In addition, two simple formulas have been established for both the bulk modulus and plasmon energy. It is found that the investigated clusters show bulk behavior.
1. Introduction
The general properties of IV materials make them useful in many fields [1-3], such as the field of electronics [4-6]. So these materials have been extensively investigated [7- 13]. The variation of material properties with pressure is an interesting field [14-15]. So, the first motive of the present work is to investigate the effect of pressure on some properties of diamond, silicon, germanium, and gray tin. The second motive is to answer the following question: Could the 216 atom clusters of these elements be regarded as nano materials or bulk materials concerning the structural properties?
A LUC (Large Unit Cell) composed of 27 unit cells (each of these units contains 8 atoms) has been used in the present analysis. The CNDO/2 method with STO (Slater Type Orbital) and LCAO (Linear Combination of Atomic Orbitals) approximation [16] was used to calculate the lattice constant, cohesive energy, total energy, and bulk modulus of the aforementioned elements. The Young modulus, microhardness, speed of sound, energy of phonons and plasmons have been also determined.
2. Calculations
The orbital exponent (ξ), bonding parameter (β), s-shell electronegativity (EES), and p-shell electronegativity (EEP), shown in Table 1 for the four elements, are the pa-
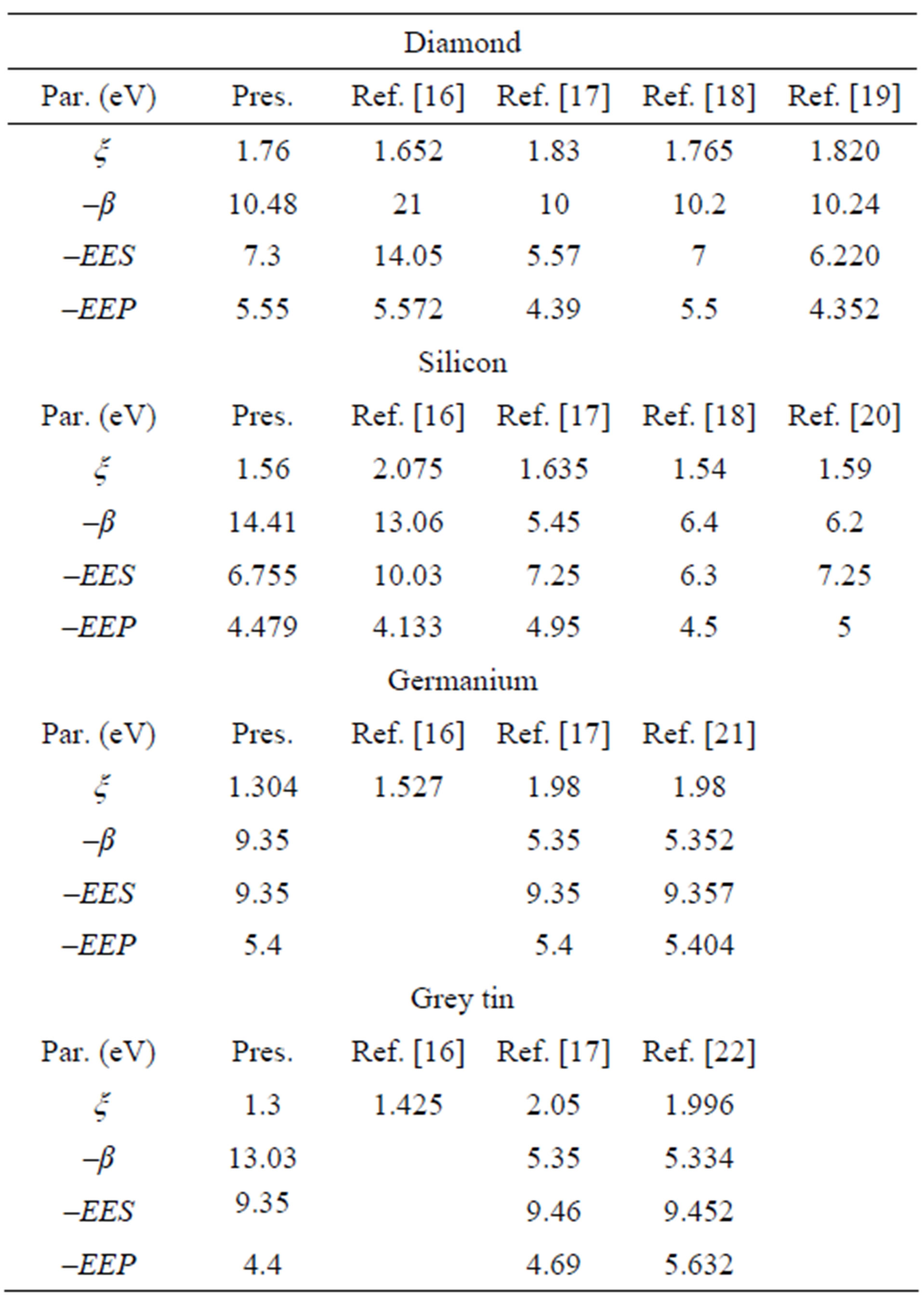
Table 1. Parameters of CNDO/2 for C, Si, Ge and α-Sn.
rameters used in the CNDO/2 method [16] to calculate the lattice constant (ao), cohesive energy (Ec) and total energy (Eo) in the ground state (zero pressure-temperature) [z-PT].
The calculated structural properties compared with other results are shown in Table 2. Our results were fitted according to Equation (1), the state equation of Murnaghan,

Table 2. The structural properties of C, Si, Ge, and α-Sn.
in order to estimate the change of energy E(V) with pressure [30].
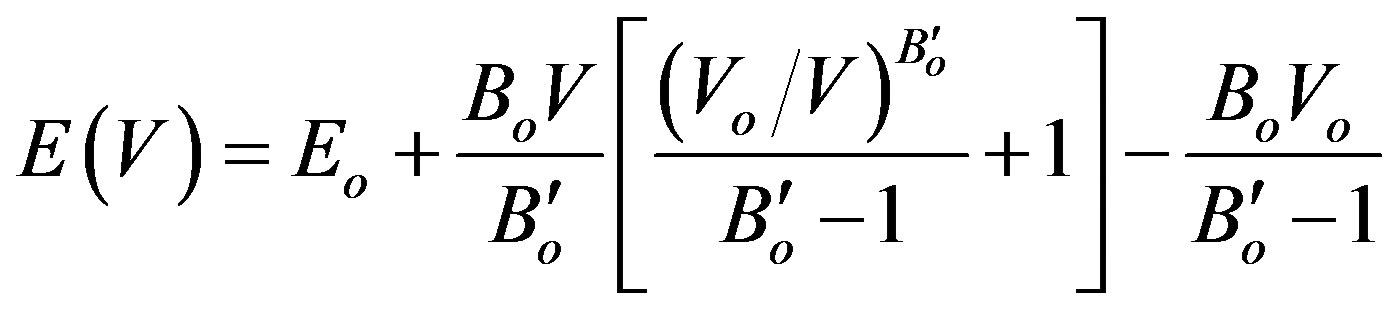 (1)
(1)
This change, using Equation (2), determines the change of vibrational energy (Fvib) [26] as below:
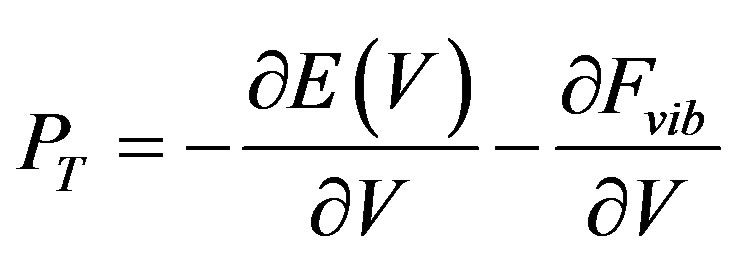 (2)
(2)
where PT is the isothermal pressure, Vo and Bo are the volume and bulk modulus of the unit cell at [z-PT], and V is the volume at any pressure.
The bulk modulus at [z-PT] is calculated using Cohen empirical formula [31]:
 (3)
(3)
where I is the ionicity factor which equals 0, 1 and 2 for IV, III-V and II-V groups respectively [31], and d (= 0.433 a) is the intratomic distance [23], where a is the lattice constant at any pressure.
Then both the isothermal bulk modulus at any pressure (BT), Equation (4) [32], and the derivative of bulk modulus at zero pressure ( ), Equation (5) [23,33], have been calculated as:
), Equation (5) [23,33], have been calculated as:
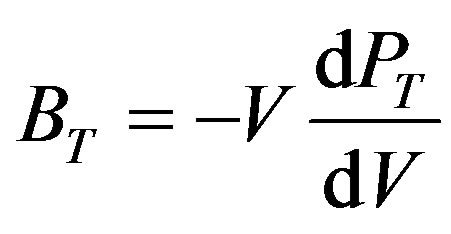 (4)
(4)
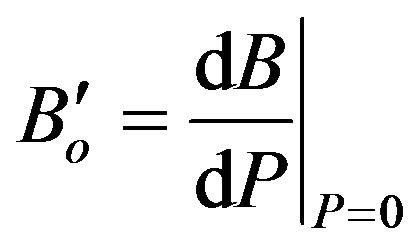 (5)
(5)
By solving Equations (4) and (5), one can get:
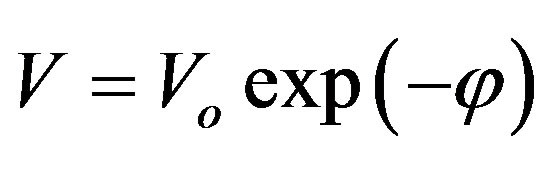 (6)
(6)
where
 (7)
(7)
The results of volume vs pressure are shown in Figure 1, in comparison with:
Ÿ Murnaghan equation of state EOS [34] of pressure (PM);
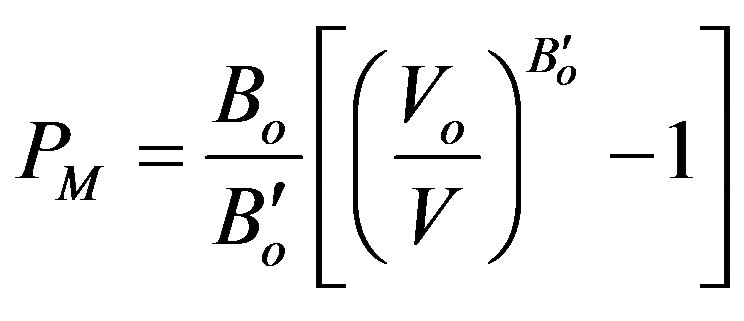 (8)
(8)
Ÿ Birch-Murnaghan EOS of pressure (PBM);
 (9)
(9)
Ÿ Vinet EOS of pressure (PBM) [35];

Figure 1. The dependence of volume upon the tensile stress, and a comparison between our general relation and each of Murnagham EOS, Birch-Murnagham EOS and Vinet EOS, for: (a) C; (b) Si; (c) Ge; and (d) α-Sn.
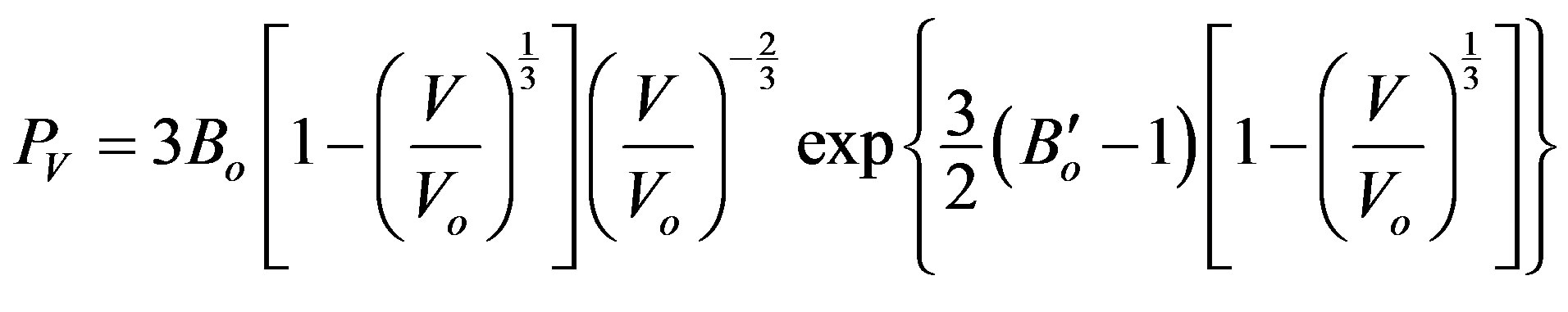 (10)
(10)
To get a wide understanding of the four elements properties, the microhardness (H) [36] and the Young modulus (E) [37] are also calculated as below:
 (11)
(11)
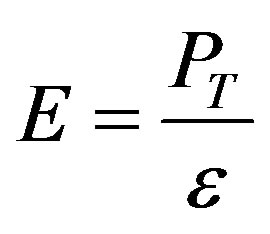 (12)
(12)
where ζ is (a/ao) and ε is the strain. Also the speed of sound (υs) is calculated as [29]:
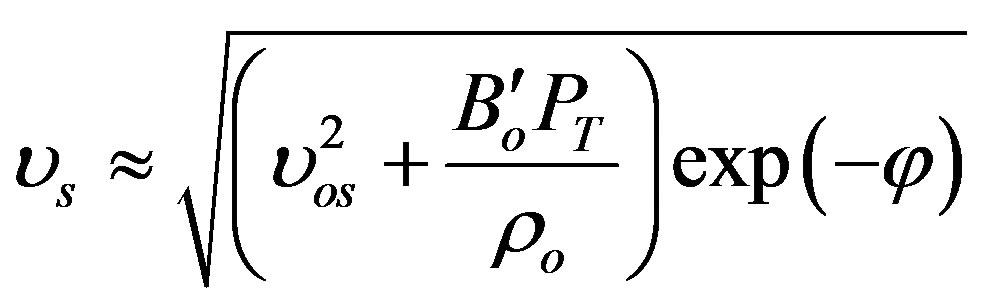 (13)
(13)
where ρo and υos are the density and the velocity of sound at [z-PT], respectively. The velocity of sound equals the average of phonons velocity (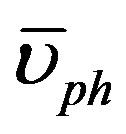 ) [38]. And from [30], the phonon velocity, angular frequency (
) [38]. And from [30], the phonon velocity, angular frequency (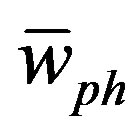 ), phonon energy (
), phonon energy ( ) and the plasmon energy (Epl) equal:
) and the plasmon energy (Epl) equal:
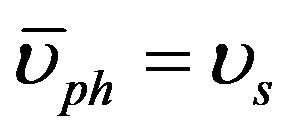 (14)
(14)
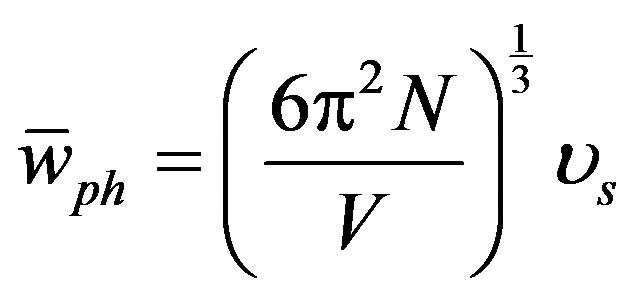 (15)
(15)
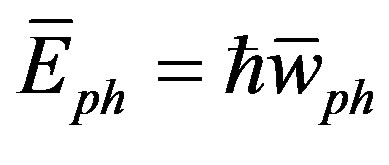 (16)
(16)
 (17)
(17)
where ne is the volume of the bond which equals [39]:
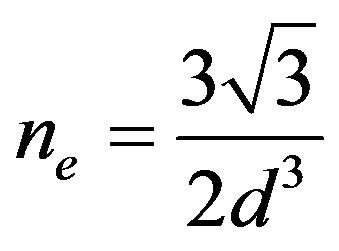 (18)
(18)
and N is the number of atoms in the unit cell which equals 8, e and m are the charge and the mass of electron respectively, and εo is the permittivity of vacuum. By gathering Equations (15), (16) and (6), one can get:
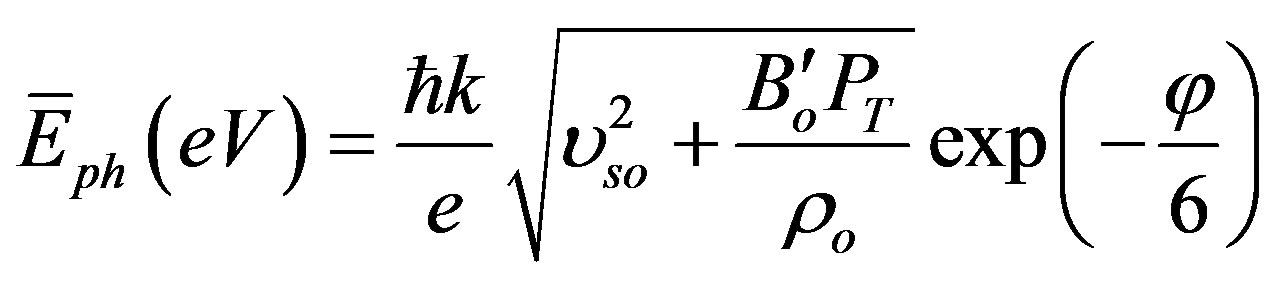 (19)
(19)
 (20)
(20)
Gathering Equations (17), (18) and (6), one can get:
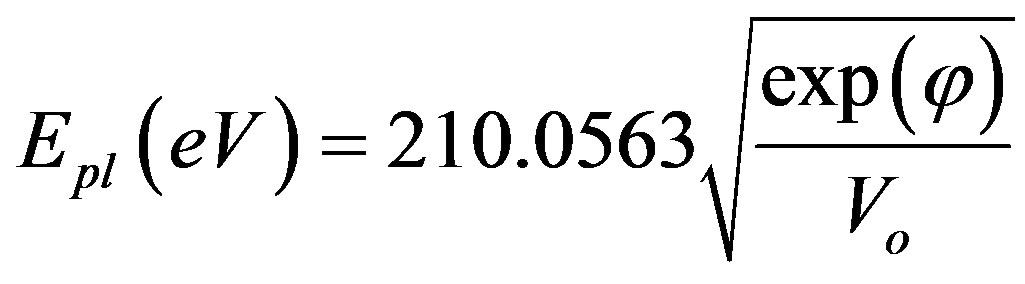 (21)
(21)
3. Results and Discussion
The results of the present work illustrated in Table 2, are in good agreement with experimental results of bulk materials. So we can assume that the structural properties of 216 atom clusters (1.21 nm, 4.32 nm, 4.89 nm, and 7.35 nm for C, Si, Ge, and Sn respectively) are properties of the corresponding bulk materials.
As shown in Figures 2 and 3, the increase of tensile stress leads to an increase of volume and a decrease in the density. Strain, caused by tensile stress, gives the following results:
1) Alterations of the orbitals [39], and an increase of the distance between atoms [40].
2) A decrease of the bond strength [41] which depends on the distance [42].
3) A decrease of the bulk modulus [43]. It is known that the bulk modulus represents the resistance of matter to the change in volume [44], and it can be considered as the sum of the bulk modulus of all atoms [45] according to the AIM (atoms in molecules) theory [46]. Because the bulk modulus depends directly upon the density [47] and the charge distribution between atoms [48,49], i.e. the bonds [44], the bulk modulus decreases with the tensile stress.
4) A decrease of the Young modulus because it depends upon the bulk modulus [47].

Figure 2. The change of density with tensile stress for: (a) C; (b) Si; (c) Ge; and (d) α-Sn.

Figure 3. Effect of the tensile stress on the bulk modulus, Young’s modulus and the microhardness for: (a) C; (b) Si; (c) Gr; and (d) α-Sn.
5) An increase of the rigidity because the tensile stress decreases the microhardness [50].
As shown in Figures 4-6, the speed of sound, the energy of phonon and the energy of plasmon decrease when the tensile stress increases.
The sound waves produce charge distribution, according to Kornyushin who has showed that the plasma affects the charge distribution and so the sound wave [51]. On the other hand, the phonon frequency affects the effective charge [52], because the effective charge depends upon the charge distribution and determines the plasma frequency [53]. According to Sanjurjo, the compressive pressure increases the effective charge for IV-IV materials and vice verse [52]. Meanwhile, depending on Burstein who has illustrated that the decrease in the effective charge decreases the plasmon frequency [53], one can find that our results of the behavior are in good agreement with experiment [52] for both the plasmon and phonon energies.
It is shown from Figure 7 that the vibrational energy increases as the tensile stress increases. Many properties of solids depend on the phonons which determine the atoms vibration [54], where the velocity of sound depends on the atoms arrangement [55]. The crystal is considered as a group of harmonic oscillators [56], according to Bornvon Kármán theory, in order that the atoms in the lattice
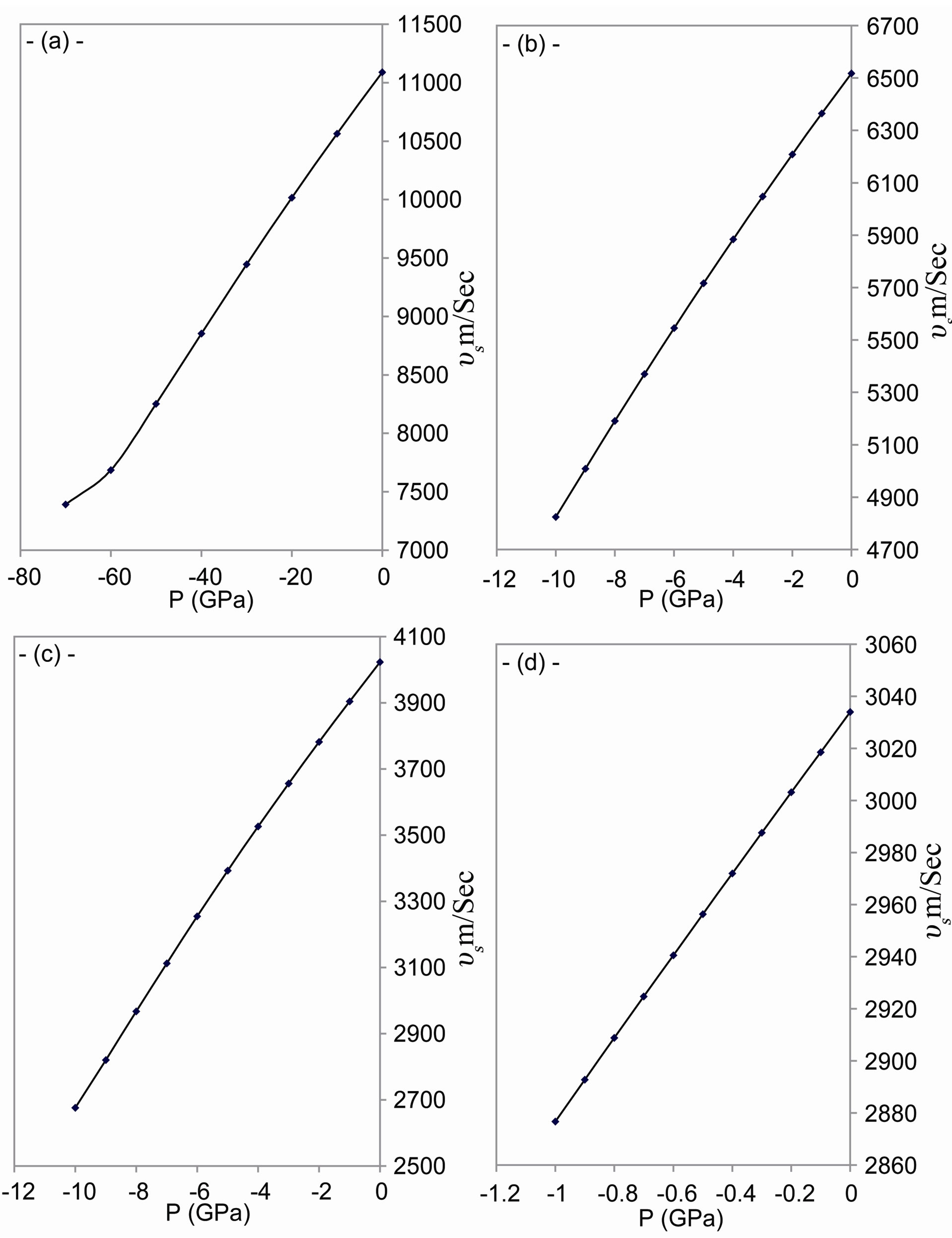
Figure 4. The change of speed of sound with tensile stress for: (a) C; (b) Si; (c) Gr; and (d) α-Sn.
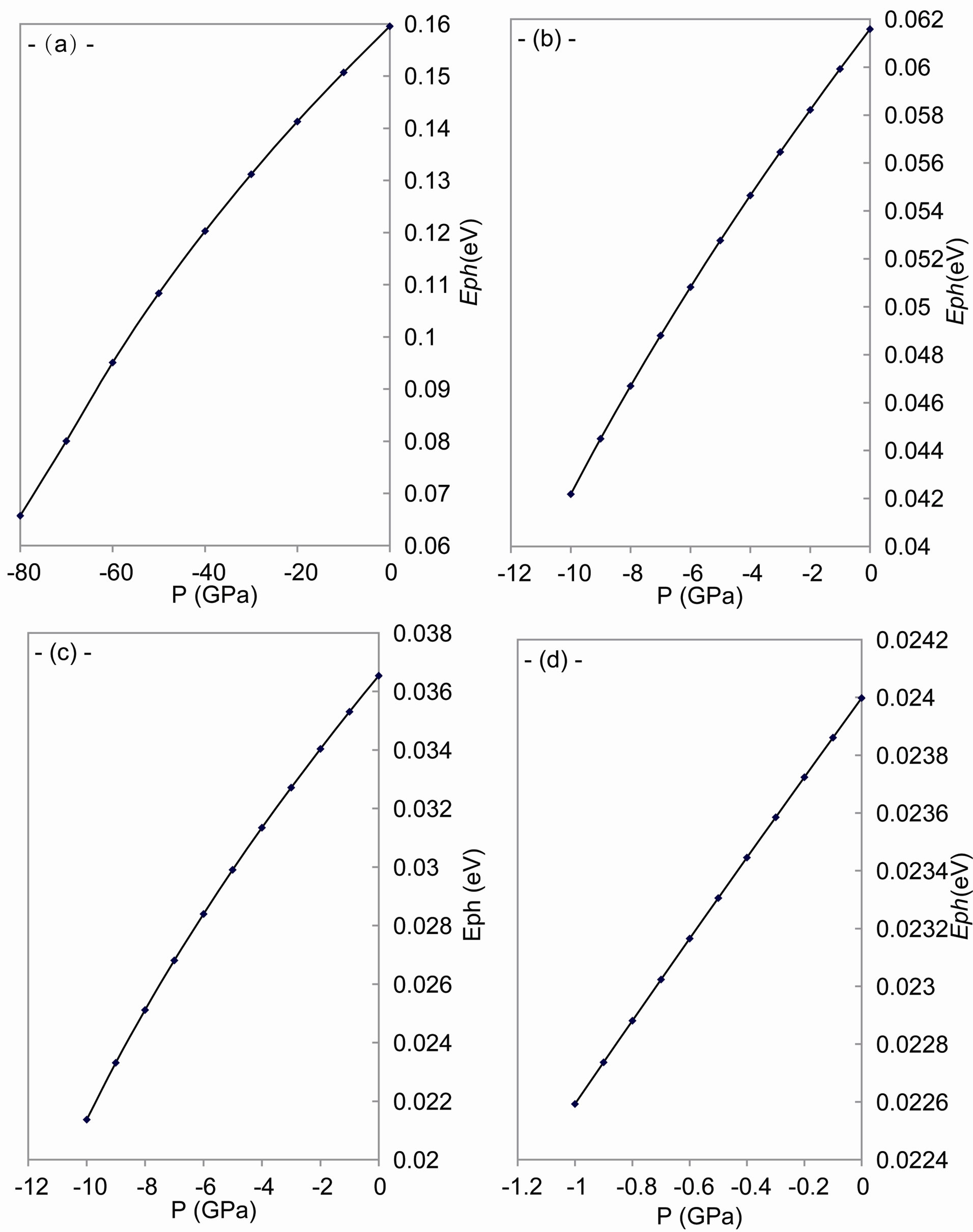
Figure 5. The change of speed of sound with tensile stress for: (a) C; (b) Si; (c) Gr; and (d) α-Sn.
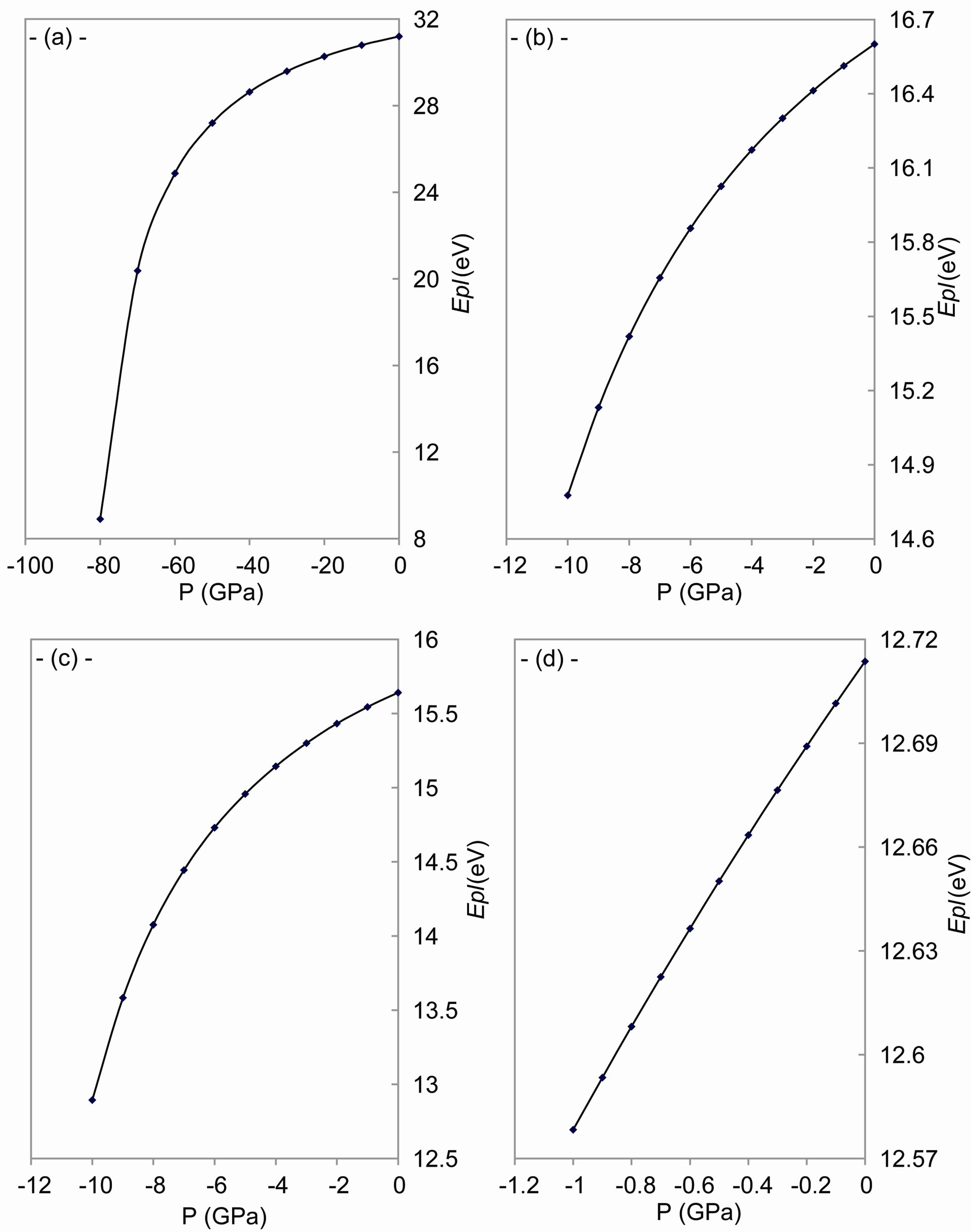
Figure 6. The change of plasmon energy with tensile stress for: (a) C; (b) Si; (c) Gr; and (d) α-Sn.

Figure 7. Effect of tensile stress on the vibrational energy for: (a) C; (b) Si; (c) Gr; and (d) α-Sn.
interplay with the nearest atoms only [57]. From all above and according to Polit who mentioned that the change of the lattice constant changes the charge distribution which affects the atoms’ force field and these potentials modify the vibration energy [58].
4. Conclusions
From the results of the present work, it can be concluded that:
1) The 216 atom clusters of C, Si, Ge, and α-Sn can be considered as bulk materials concerning the structural properties.
2) The range of the elastic deformation for diamond is the smallest.
3) The higher the tensile stress, the higher the rigidity of the sample.
4) The inclusion of the bulk modulus in every change may be very important in some properties because it can limit their variation range caused by external factors.
5) The relation of phonons gives approximated results, however, it is simple and could be used for behavior study.
REFERENCES
- F. Cataldo, “Carbon Allotropy and Carbon Black,” Kautschuk Gummi Kunststoffe, Vol. 54, No. 1-2, 2001, pp. 22-28.
- C. W. Myles, J. Dong and O. F. Sankey, “Structural and Electronic Properties of Tin Clathrate Materials,” Physical Review B, Vol. 64, No. 16, 2001, pp. 165202-165212. doi:10.1103/PhysRevB.64.165202
- M. Gaith and I. Alhayek, “Correlation between Overall Elastic Stiffness, Bulk Modulus and Interatomic Distance in Anisotropic Materials: Semiconductors,” Reviews on Advanced Materials Science, Vol. 21, No. 2, 2009, pp. 183-191.
- M. Gabrysch, “Electronic Properties of Diamond,” Uppsala University, 2008. http://urn.kb.se/resolve?urn=urn:nbn:se:uu:diva-8675
- M. Virgilio, G. Pizzi and G. Grosso, “Optical Gain in Short Period Si/Ge Superlattices on [001]-SiGe Substrates,” Journal of Applied Physics, Vol. 110, No. 8, 2011, pp. 083105-083112. doi:10.1063/1.3651196
- M. Upadhyay, S. Murugavel, M. Anbarasu and T. R. Ravindran, “Structural Study on Amorphous and Crystalline State of Phase Change Material,” Journal of Applied Physics, Vol. 110, No. 8, 2011, pp. 083711-083716. doi:10.1063/1.3653265
- R. E. Stallcup II, L. M. Villarreal, S. C. Lim, I. Akwani, A. F. Aviles and J. M. Perez, “Atomic Structure of the Diamond (100) Surface Studied Using Scanning Tunneling Microscopy,” Journal of Vacuum Science and Technology B, Vol. 14, No. 2, 1996, pp. 929-932. doi:10.1116/1.589177
- B. K. Serdega, E. V. Nikitenko and Prikhodenko, “Effect of Surface Condition on Strain in Semiconductor Crystal Sample,” Semiconductor Physics, Quantum Electronics and Optoelectronics, Vol. 4, No. 1, 2001, pp. 9-11.
- J. Pollmann, P. Krüger, M. Rohlfing, M. Sabisch and D. Vogel, “Ab Initio Calculations of Structural and Electronic Properties of Prototype Surfaces of Group IV, III-V and II-VI Semiconductors,” Applied Surface Science, Vol. 104-105, 1996, pp. 1-16. doi:10.1016/S0169-4332(96)00114-6
- A. Otero-de-la-Roza and V. Luaña, “Topological Characterization of the Electron Density Laplacian in Crystals. The Case of the Group IV Elements,” Journal of Chemical Theory and Computation, Vol. 6, No. 12, 2010, pp. 3761-3979. doi:10.1021/ct100269e
- L. A. Woldering, L. Abelmann and M. C. Elwenspoek, “Predicted Photonic Band Gaps in Diamond-Lattice Crystals Built from Silicon Truncated Tetrahedrons,” Journal of Applied Physics, Vol. 110, No. 4, 2011, pp. 043107- 043114. doi:10.1063/1.3624604
- Q. Zhou, X. Hu, K. Al-Hemyari, K. McCarthy, L. Domash and J. A. Hudgings, “High Spatial Resolution Characterization of Silicon Solar Cells Using Thermoreflectance Imaging,” Journal of Applied Physics, Vol. 110, No. 5, 2011, pp. 053108-053113. doi:10.1063/1.3629979
- J. Kim and D. Ahn, “Effect of Indirect Interband Absorption in Ge/SiGe Quantum Wells,” Journal of Applied Physics, Vol. 110, No. 8, 2011, pp. 083119-083128. doi:10.1063/1.3656688
- C. Q. Sun, “Size Dependence of Nanostructures: Impact of Bond Order Deficiency,” Progress in Solid State Chemistry, Vol. 35, No. 1, 2007, pp. 1-159. doi:10.1016/j.progsolidstchem.2006.03.001
- M. M. Shokrieh and R. Rafiee, “Prediction of Young’s Modulus of Graphene Sheets and Carbon Nanotubes Using Nanoscale Continuum Mechanics Approach,” Materials and Design, Vol. 31, No. 2, 2010, pp. 790-795. doi:10.1016/j.matdes.2009.07.058
- J. A. Pople and D. L. Beveridge, “Approximate Molecular Orbital Theory,” McGraw-Hill, New York, 1970.
- M. A. Abdulsattar, “Self Consistent Field Calculations of Covalent Semiconductors,” Ph.D. Thesis, University of Baghdad, Baghdad, 1997.
- B. S. M. Baaee, “Theoretical Process to Study the Band Structure of Germanium Crystal by Use the Intermediate Neglect of Differential Overlap Method,” M.Sc. Thesis, University of Babylon, Babylon, 2003.
- I. O. R. Al-Jelawy, “Effect of Pressure and Temperature on Some Properties of Diamond Crystal Using HartreeFock Method,” M.Sc. thesis, University of Babylon, Babylon, 2005.
- M. M. Al-Hello, “Study of the Effect of Pressure on the Properties of Si-Crystal Using Semiempirical Method,” M. Sc. Thesis, University of Babylon, Babylon, 2004.
- A. H. Harker and F. P. Larkins, “A Large Unit Cell Semiempirical Molecular Orbital Approach to the Properties of Solids II. Covalent Materials: Diamond and Silicon,” Journal of Physics C: Solid State Physics, Vol. 12, 1979, pp. 2497-2507. doi:10.1088/0022-3719/12/13/014
- M. G. Merdan, “Self-Consistent Field Calculations for the Effect of Pressure and Temperature on Some Properties of Grey Tin Crystal,” M.Sc. Thesis, University of Babylon, Babylon, 2005.
- S. Q. Wang and H. Q. Ye, “Plane-Wave Pseudopotential Study on Mechanical and Electronic Properties for IV and III-V Crystalline Phases with Zinc-Blende Structure,” Physical Review B, Vol. 66, No. 23, 2002, pp. 235111- 235117. doi:10.1103/PhysRevB.66.235111
- S. H. Lee, J. H. Kang and M. H. Kang, “Structural Properties of Semiconductors in the Generalized Gradient Approximation,” Journal of the Korean Physical Society, Vol. 31, No. 3, 1997, pp. 811-814.
- J. S. Blakemore, “Solid State Physics,” 2nd Edition, Cambridge University Press, Cambridge, 1985.
- J. Xie, S. P. Chen, J. S. Tse, S. de Gironcoli and S. Baroni, “High-Pressure Thermal Expansion, Bulk Modulus, and Phonon Structure of Diamond,” Physical Review B, Vol. 60, No. 13, 1999, pp. 9444-9449. doi:10.1103/PhysRevB.60.9444
- C. Kittel, “Introduction to Solid State Physics,” 7th Edition, John Wiley and Sons, Hoboken, 1996.
- A. Mujica, A. Rubio, A. Munoz and R. J. Need, “High Pressure Phaces of Group-IV, III-V, and II-VI Compounds,” Reviews of Modern Physics, Vol. 75, No. 3, 2003, pp. 863-907. doi:10.1103/RevModPhys.75.863
- B. Akdim, D. A. Papaconsttantopoulos and M. J. Mehl, “Tight-Binding Description of the Electronic Structure and Total Energy of Tin,” Philosophy Magazine B, Vol. 82, No. 1, 2002, pp. 47-61. doi:10.1080/13642810208211215
- C. A. Perottoni, A. S. Pereira, and J. A. H. da Jornada, “Periodic Hartree-Fock Linear Combination of Crystalline Orbitals Calculation of the Structure, Equation of State and Elastic Properties of Titanium Diboride,” Journal of Physics: Condensed Matter, Vol. 12, No. 32, 2000, pp. 7205-7222. doi:10.1088/0953-8984/12/32/305
- J. Zheng, C. H. A. Haun, A. T. S. Wee, R. Wang and Y. Zheng, “Ground State Properties of Cubic C-BN Solid Solutions,” Journal of Physics: Condensed Matter, Vol. 11, No. 3, 1999, pp. 927-935. doi:10.1088/0953-8984/11/3/030
- T. Faisst, “Temperature Dependence of the Thermal Expansion Coefficient, Bulk Modulus and Magnetic Grueneisen Constant of Nickel Near the Curie Point,” Journal De Physique, Vol. 49, No. 12, 1988, pp. 65-66. doi:10.1051/jphyscol:1988819
- P. E. Van Camp, V. E. Van Doren, and J. T. Devreese, “Ground-State and Electronic Properties of Covalent Solids,” Physical Review, Vol. 38, No. 17, 1988, pp. 12675-12678. doi:10.1103/PhysRevB.38.12675
- S. Q. Wang, H. Q. Ye and S. Yip, “First Principles Studies on the Pressure Dependences of the Stress Strain Relationship and Elastic Stability of Semiconductors,” Physics: Condensed Matter, Vol. 18, No. 2, 2006, pp. 395- 409. doi:10.1088/0953-8984/18/2/004
- C. Narayana, V. J. Nesamony, and A. L. Ruoff, “Phase Transformation of BeS and Equation-Of-State Studies to 96 GPa,” Physical Review B, Vol. 56, No. 22, 1997, pp. 14338-14343.
- R. Asokamani and R. Rita, “Electronic Structure and Physical Properties of ABC2 (A = Zn, B = Si, Ge, Sn, and C = P, As) Ternary Penictide Semiconductors,” Physica Status Solidi B, Vol. 226, No. 2, 2001, pp. 375-384. doi:10.1002/1521-3951(200108)226:2<375::AID-PSSB375>3.0.CO;2-8
- W. Kim, M. Kim, Y. Chang, J. Shin and J. Bae, “Fatigue Crack Growth Behavior of NR and HNBR Based Vulcanizates with Potential Application to Track Pad for Heavy Weight Vehicles,” Macromolecular Research, Vol. 11, No. 2, 2003, pp. 73-79. doi:10.1007/BF03218333
- G. D. Raj, “Solid State Physics,” 1st Edition, Anmol Publication Pvt. Ltd, New Delhi, 2004.
- V. Kumar and B. S. R. Sastry, “Thermal Expansion Coefficient of Binary Semiconductors,” Crystal Research and Technology, Vol. 36, No. 6, 2001, pp. 565-569.
- J. P. Connerade, P. Kengkan, P. A. Lakshmi and R. Semaoune, “Scaling Laws for Atomic Compressibility,” Journal of Physics B: Atomic and Molecular Optical Physics, Vol. 33, No. 22, 2000, pp. L847-L854.
- S. M. Sze, “Semiconductor Devices: Physics and Technology,” Dar Al-Hikma, Mosul, 1990.
- J. Z. Jiang, H. Lindelov, L. Gerward, K. Ståhl, J. M. Recio, P. Mori-Sanchez, S. Carlson, M. Mezouar, E. Dooryhee, A. Fitch and D. J. Frost, “Compressibility and Thermal Expansion of Cubic Silicon Nitride,” Physical Review B, Vol. 65, No. 16, 2002, pp. 161202-161205. doi:10.1103/PhysRevB.65.161202
- Y. Sun, S. E. Thompson and T. Nishida, “Physics of Strain Effects in Semiconductors and Metal-Oxide-Semiconductor Field-Effect Transistors,” Journal of Applied Physics, Vol. 101, No. 10, 2007, pp. 104503-104522. doi:10.1063/1.2730561
- M. P. D’Evelyn and T. Taniguchi, “Elastic Properties of Translucent Polycrystalline Cubic Boron Nitride as Characterized by the Dynamic Resonance Method,” GE Research & Development Center, General Electric Company, 1998.
- M. Mattesini and S. F. Matar, “First Principle Characterization of New Ternary Heterodiamond BC2N Phases,” Computational Materials Science, Vol. 20, No. 2, 2001, pp. 107-119. doi:10.1016/S0927-0256(00)00132-4
- A. M. Pendás, A. Costales, M. A. Blanco, J. M. Recio and V. Luanã, “Local Compressibilities in Crystals,” Physical Review B, Vol. 62, No. 21, 2000, pp. 13970-13978. doi:10.1103/PhysRevB.62.13970
- A. M. Pendás, “Stress, Virial, and Pressure in the Theory of Atoms in Molecules,” Journal of Chemical Physics, Vol. 117, No. 3, 2002, pp. 965-979. doi:10.1063/1.1484385
- B. T. Wang, P. Zhang, H. L. Shi, B. Sun and W. D. Li, “Mechanical and Chemical Bonding Properties of Ground State BeH2,” The European Physical Journal B, Vol. 74, No. 3, 2010, pp. 303-308. doi:10.1140/epjb/e2010-00081-x
- G. E. Fernandez, S. A. Serebrinsky, J. L. Gervasoni and J. P. Abriata, “Calculation of the Pressure Dependence of the Bulk Modulus Using a Jelliumm Model,” International Journal of Hydrogen Energy, Vol. 29, 2004, pp. 93-95. doi:10.1016/S0360-3199(03)00050-8
- S. Barzilai, I. Halevy and O. Yeheskel, “Bulk Modulus of Sc2O3: Ab Initio Calculations and Experimental Results,” Journal of Applied Physics, Vol. 110, No. 4, 2011, p. 043532. doi:10.1063/1.3626457
- B. Yu, D. Chen, Q. Tang, C. Wang and D. Shi, “Structural, Electronic, Elastic and Thermal Properties of Mg2Si,” Journal of Physics and Chemstry of Sollids, Vol. 71, No. 5, 2010, pp. 758-763. doi:10.1016/j.jpcs.2010.01.017
- L. C. M. Miranda and D. ter Haar, “Plasma Effects in Sound Amplification in Piezo-Electric Semiconductors,” Revista Brasileira de Física, Vol. 2, No. 2, 1972, pp. 77- 86.
- J. A. Sanjurjo, E. López-Cruz, P. Vogl and M. Cardona, “Dependence on Volume of the Phonon Frequencies and the IR Effective Charges of Several III-V Semiconductors,” Physical Review B, Vol. 28, No. 8, 1983, pp. 4579- 4584. doi:10.1103/PhysRevB.28.4579
- E. Burstein, S. Perkowitz and M. H. Brodsk, “The Dielectric Properties of the Cubic IV-VI Compound Semiconductors,’’ Journal De Physique, Vol. 29, No. 11-12, 1968, pp. 78-83. doi:10.1051/jphyscol:1968411
- K. Parliński, “First-Principles Calculations of Vibrational and Thermodynamical Properties of Solids,” Materials Science-Poland, Vol. 23, No. 2, 2005, pp. 357-363.
- T. Iitaka and T. Ebisuzaki, “First-Principles Calculation of Elastic Properties of Solid Argon at High Pressures,” Riken Review, No. 48, 2001, pp. 12-15.
- J. Xie, S. de Gironcoli, S. Baroni and M. Scheffler, “First-Principles Calculation of the Thermal Properties of Silver,” Physical Review B, Vol. 59, No. 2, 1999, pp. 965-969. doi:10.1103/PhysRevB.59.965
- C. Malinowska-Adamska, P. Sloma and J. Temaszewski, “Physical Properties of Ni fcc Lattice in Terms of the Self-Consistent Phonon Theory,” Journal of Physics: Condensed Matter, Vol. 18, No. 2, 2006, pp. 751-758. doi:10.1088/0953-8984/18/2/028
- J. Polit, E. M. Sheregii, J. Cebulski, B. V. Robouch, A. Marcelli, M. Cestelli Guidi, M. Piccinini, A. Kisiel, P. Zajdel, E. Burattini and A. Mycielski, “Phonon and Vibrational Spectra of Hydrogenated CdTe,” Journal of Applied Physics, Vol. 100, No. 1, 2006, p. 013521. doi:10.1063/1.2211368
NOTES
*Corresponding author.

