World Journal of Condensed Matter Physics
Vol.1 No.4(2011), Article ID:8767,8 pages DOI:10.4236/wjcmp.2011.14020
Ferro- and Antiferromagnetic Aspects of Alternating Spin Systems
![]()
Department of Physics, Alaith collage for girls, Umm Alqura University, Mecca, KSA.
Email: aiman_101@hotmail.com, aaomari@uqu.edu.sa
Received June 13th, 2011; revised August 10th, 2011; accepted August 25th, 2011.
Keywords: Spin wave theory, Alternating spins, Specific heat, Schottky peak, Susceptibility
ABSTRACT
Using linear spin-wave theory we have investigated the thermal properties of frustrated dimerized Heisenberg ferrimagnetic system with alternating spins 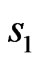 and
and 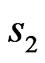 on oneand two-dimensional lattices. At intermediate temperature the susceptibility
on oneand two-dimensional lattices. At intermediate temperature the susceptibility 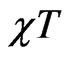 and the specific heat
and the specific heat 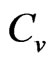 shows a minimum and a Schottky-like peak respectively. Frustration enhances the antiferromagnetic aspect in the system by causing a left-shift in the peak and the minimum which indicates that the antiferromagnetic behavior overbalance the ferromagnetic one at earlier temperatures. The effect of dimerization is different for the two form of the coupling constants. While the expanded form;
shows a minimum and a Schottky-like peak respectively. Frustration enhances the antiferromagnetic aspect in the system by causing a left-shift in the peak and the minimum which indicates that the antiferromagnetic behavior overbalance the ferromagnetic one at earlier temperatures. The effect of dimerization is different for the two form of the coupling constants. While the expanded form;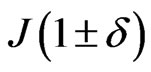 , boosts the antiferromagnetic behavior of the system by making a left-shift of the peak and the minimum, the distance-variable coupling constant;
, boosts the antiferromagnetic behavior of the system by making a left-shift of the peak and the minimum, the distance-variable coupling constant; 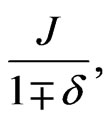 shifts them to the right opposing, for a while, the appearance of the antiferromagnetic aspect. The slope of
shifts them to the right opposing, for a while, the appearance of the antiferromagnetic aspect. The slope of 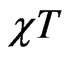 after the minimum shows that the aspect of ferrimagnetic system with spins (3/2, 1) is more antiferromagnetic and the system with (3/2, 1/2) is ferromagnetic. Free energy and magnetization decreased by increasing dimerization as well as frustration. Both of them scales with
after the minimum shows that the aspect of ferrimagnetic system with spins (3/2, 1) is more antiferromagnetic and the system with (3/2, 1/2) is ferromagnetic. Free energy and magnetization decreased by increasing dimerization as well as frustration. Both of them scales with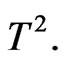 PACS numbers: 75.10.Jm, 75.50.Ge.
PACS numbers: 75.10.Jm, 75.50.Ge.
1. Introduction
Many attentions were made towards the low-dimensional antiferromagnets after Halden made his prediction that the integer-spin chain is massive, whereas the half-oddinteger spin chain is massless. This stimulated also several attempts to investigate the quantum behavior of chains consisting of two types of spins. An integrable model of this type was constructed by De Vega and Woynarovich [1], which allows us to guess the essential consequences of chains with spins of different length S. Recently [2], several authors discussed in detail such a bimetallic chain with spins s = 1 and 1/2 as the simplest case.
The thermal behavior was also investigated for ferrimagnetic chains [3-13]. Besides verifying the existence of two (gapped and gapless) excitation modes, the specific heat and magnetic susceptibility of ferrimagnetic chains were shown to depend upon temperature as 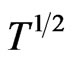 and
and 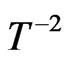 respectively at low temperatures using modified spinwave theory (MSWT) [6,7], density matrix renormalizetion group (DMRG) [7], quantum Monte Carlo method (QMC) [6,7,11], and Schwinger boson mead field theory (SB) [5]. Susceptibility was shown to has a minimum at intermediate temperature [3-5,7]. Specific heat was having a maximum [3,4,7,9-13] at mid temperature showing a Schottky-like peak. The spin correlation length behaves as
respectively at low temperatures using modified spinwave theory (MSWT) [6,7], density matrix renormalizetion group (DMRG) [7], quantum Monte Carlo method (QMC) [6,7,11], and Schwinger boson mead field theory (SB) [5]. Susceptibility was shown to has a minimum at intermediate temperature [3-5,7]. Specific heat was having a maximum [3,4,7,9-13] at mid temperature showing a Schottky-like peak. The spin correlation length behaves as 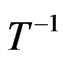 at low temperature [6,8]. Using those techniques, it was shown also that the ferromagnetic behavior vanishes by increasing
at low temperature [6,8]. Using those techniques, it was shown also that the ferromagnetic behavior vanishes by increasing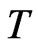 , while the antiferromagnetic one persists up to higher temperatures.
, while the antiferromagnetic one persists up to higher temperatures.
Modified spin wave theory, which includes Takahashi constraint or non-linear spin wave theory, was also shown to give results in surprisingly good agreement with those from quantum Monte Carlo method in the thermodynamic limit of this system [6,7].
In this paper we will study alternating spin systems formed with a spin values; (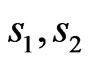 ) using linear spin wave theory. We would like to investigate the thermal properties of the lattice magnetization, specific heat, free energy, and susceptibility. We would like to see how their thermal behavior depends on dimerization and frustration. We shall then study alternating spin systems on a square lattice.
) using linear spin wave theory. We would like to investigate the thermal properties of the lattice magnetization, specific heat, free energy, and susceptibility. We would like to see how their thermal behavior depends on dimerization and frustration. We shall then study alternating spin systems on a square lattice.
2. One Dimensional Alternating System
The dimerization of chains with spins 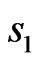 and
and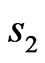 (
(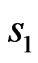 >
>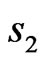 ) on alternating sites with competing antiferromagnetic nearest and next nearest neighbor couplings,
) on alternating sites with competing antiferromagnetic nearest and next nearest neighbor couplings, 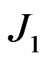 and
and 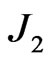 respectively, may be described by the Hamiltonian
respectively, may be described by the Hamiltonian
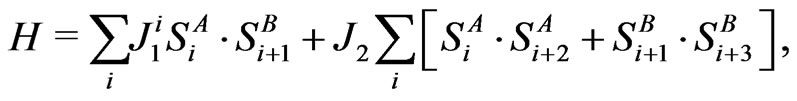 (1)
(1)
with 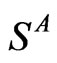 belongs to the first sublattice with spin
belongs to the first sublattice with spin 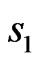 and
and 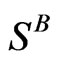 to the second one with spin
to the second one with spin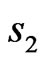 .
. 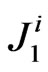 is the alternating coupling between two adjacent sites, it gives the displacement of the ith atom through
is the alternating coupling between two adjacent sites, it gives the displacement of the ith atom through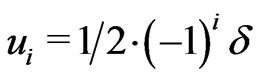 . The exchange coupling constants defined in Equation (1) can have different forms. In order to take into account changing distances in the course of spin-Peierls distortions, we assume that the nearest-neighbor spin-spin exchange coupling is itself distance dependent [13]
. The exchange coupling constants defined in Equation (1) can have different forms. In order to take into account changing distances in the course of spin-Peierls distortions, we assume that the nearest-neighbor spin-spin exchange coupling is itself distance dependent [13]
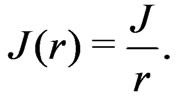 (2)
(2)
instead of the often-used 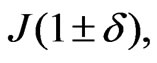 which in any case is an approximation of
which in any case is an approximation of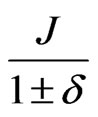 .
.
The above Hamiltonian can be linearized using spinwave analysis with the help of Holstein-Primakoff transformations to bosonic spin-deviation operators. The linearized Hamiltonian can be diagonalized using Bogoliubov transformations in terms of normal modes as
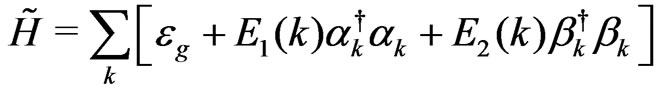 (3)
(3)
with 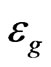 is the ground state energy and
is the ground state energy and 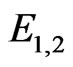 are the acoustic and a optical modes for this system. A detailed study of the above system at zero temperature was discussed in our previous paper [2].
are the acoustic and a optical modes for this system. A detailed study of the above system at zero temperature was discussed in our previous paper [2].
The free energy of the system is obtained by
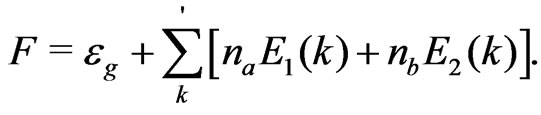 (4)
(4)
Static susceptibility 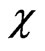 is obtained by taking thermal averages [14] of the longitudinal correlations as
is obtained by taking thermal averages [14] of the longitudinal correlations as
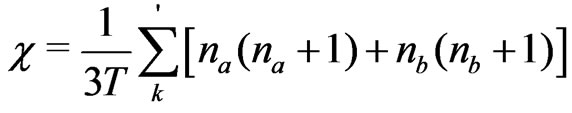 (5)
(5)
The sublattice magnetization is calculated by taking the thermal average of the occupation number as
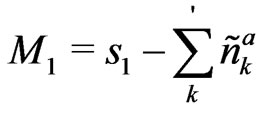 (6)
(6)
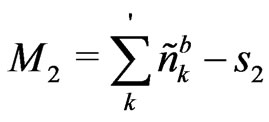 (7)
(7)
and
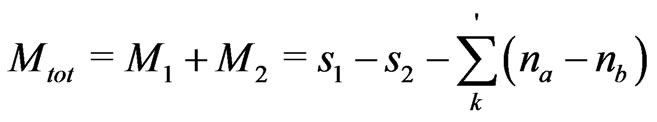 (8)
(8)
where 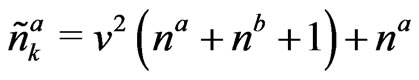 ,
,
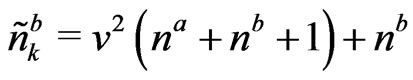
and 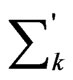 runs over half of Brillouin zone and
runs over half of Brillouin zone and 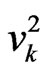 is the coefficient in Bogoliubov transformation; see Ref. [2].
is the coefficient in Bogoliubov transformation; see Ref. [2].  and
and  are bose distribution functions. Specific heat
are bose distribution functions. Specific heat 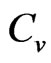 is calculated by taking the differentiation of the free energy with respect to
is calculated by taking the differentiation of the free energy with respect to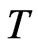 .
.
The behavior of these physical quantities with temperature in presence of dimerization 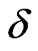 and frustration
and frustration 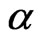 parameters for different system
parameters for different system 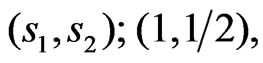
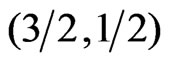 and
and 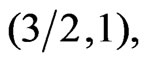 shall be discussed below. In chains we will investigate the thermal behavior using the expanded form of the coupling constant first and make a comparison with the behavior when the unexpanded form is used.
shall be discussed below. In chains we will investigate the thermal behavior using the expanded form of the coupling constant first and make a comparison with the behavior when the unexpanded form is used.
2.1. Dimerized Chains with α = 0
2.1.1. Using Expanded Form
In a previous work [15] the thermal properties of chains were investigated for this kind exchange coupling constant and reported. We will mention briefly the results here for the sake of comparison. Free energy decrease with increasing temperature regardless the magnitude values of spins 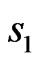 and
and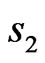 . At T = 0 it shows the ground state energy of the system. It was founded that dimerization at T = 0 reduces ground state energy [2,16], it does the same with free energy. We found that the decrease of the free energy goes as
. At T = 0 it shows the ground state energy of the system. It was founded that dimerization at T = 0 reduces ground state energy [2,16], it does the same with free energy. We found that the decrease of the free energy goes as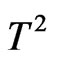 .
.
Total magnetization decreases with increasing T and 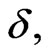 with a slower decrease for higher dimerization. This decrease shows a power law behavior goes as
with a slower decrease for higher dimerization. This decrease shows a power law behavior goes as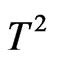 .
.
It is known that ferromagnetic materials show a decaying susceptibility with temperature and increasing for antiferromagnet. Ferrimagnets are believed to have a combined effect of both behaviors [4,8,9,17-19], ferromagnetic and antiferromagnetic. Susceptibility times temperature decreases at low temperature showing a minimum and them starts to increase showing that the antiferromagnetic behavior is not smeared out after the minimum. Activating the effect of dimerization, we found that dimerization pushes  up and causes a shift of this minimum to lower values of T at larger values of
up and causes a shift of this minimum to lower values of T at larger values of 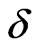 for all the three spin systems discussed here. The slope after the minimum varies form spin system to another. While the slop changes minutely with increasing dimerization parameter
for all the three spin systems discussed here. The slope after the minimum varies form spin system to another. While the slop changes minutely with increasing dimerization parameter 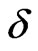 in the case of (
in the case of (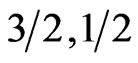 ) it is much visible for (
) it is much visible for (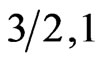 ). This behavior indicates that the spin system (
). This behavior indicates that the spin system (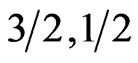 ) acts like antiferromagnetic system than a ferromagnetic one. It is vise versa for the system (
) acts like antiferromagnetic system than a ferromagnetic one. It is vise versa for the system (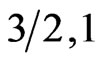 ) This conclusion is in agreement with earlier one saying that the system with
) This conclusion is in agreement with earlier one saying that the system with 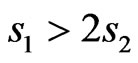 is more ferromagnetic and the system with
is more ferromagnetic and the system with 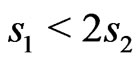 is more antiferromagnetic.
is more antiferromagnetic.
Specific heat increases at low T, and goes as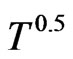 , till it reaches a maximum where it shows a shocttky-like peak at intermediate temperature and then starts to decrease again. The antiferromagnetic excitation mode plays a major rule to this peak because it is gapped at
, till it reaches a maximum where it shows a shocttky-like peak at intermediate temperature and then starts to decrease again. The antiferromagnetic excitation mode plays a major rule to this peak because it is gapped at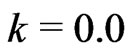 , showing that after this peak the antiferromagnetic behavior is predominant. This peak is softening with the increase of dimerization parameter and shifts towards lower values of temperature. While at low temperature dimerization enhances the specific heat,
, showing that after this peak the antiferromagnetic behavior is predominant. This peak is softening with the increase of dimerization parameter and shifts towards lower values of temperature. While at low temperature dimerization enhances the specific heat, 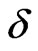 reduces it at intermediate T for the three spin systems. We notice that at high
reduces it at intermediate T for the three spin systems. We notice that at high 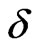 specific heat become double peaked. This tell us that the ferromagnetic and antiferromagnetic modes are still gapless and gapped modes [20]. The double peak was not seen in the system with spins
specific heat become double peaked. This tell us that the ferromagnetic and antiferromagnetic modes are still gapless and gapped modes [20]. The double peak was not seen in the system with spins 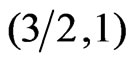 at least in our range of temperature.
at least in our range of temperature.
2.1.2. Using 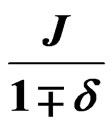 as a Coupling Constant
as a Coupling Constant
As mentioned above, using 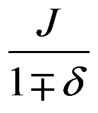 as a coupling constant is not of much important in the chains as it should be for the case of a square lattice. But we will investigate the thermal behavior of chains using the distance dependence coupling constant for the sake of having a complete picture of this form.
as a coupling constant is not of much important in the chains as it should be for the case of a square lattice. But we will investigate the thermal behavior of chains using the distance dependence coupling constant for the sake of having a complete picture of this form.
At zero temperature analysis [14] the acoustic mode showed a peculiar behavior with both forms of the coupling constants. While in the expanded form dimerization suppressed this mode the 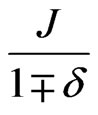 used to enhance it. The same peculiar behavior was observed in the gapless mode at any finite temperature.
used to enhance it. The same peculiar behavior was observed in the gapless mode at any finite temperature.
Free energy as well as total lattice magnetization show qualitatively a similar thermal behavior as the expand coupling constant one. Both were founded to decrease with increasing temperature, regardless the magnitude values of spins 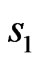 and
and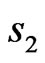 , and both of them decrease with
, and both of them decrease with 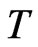 as
as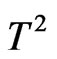 .
.
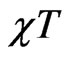 decreases at low temperature showing a minimum and them starts to increase showing that the antiferromagnetic behavior is not smeared out after the minimum. We found that dimerization in this case suppresses
decreases at low temperature showing a minimum and them starts to increase showing that the antiferromagnetic behavior is not smeared out after the minimum. We found that dimerization in this case suppresses 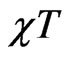 and shifts the minimum toward a higher values of T with the increase of
and shifts the minimum toward a higher values of T with the increase of 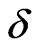 for all the three spin systems. The slope after the minimum varies form spin system to another. While the slop changes minutely with increasing dimerization parameter
for all the three spin systems. The slope after the minimum varies form spin system to another. While the slop changes minutely with increasing dimerization parameter 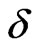 in the case of (
in the case of (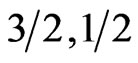 ), it is more visible for (
), it is more visible for (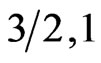 ) and it is the most for (
) and it is the most for (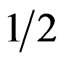 ). This behavior indicates that the spin system (
). This behavior indicates that the spin system (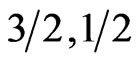 ) acts like antiferromagnetic system than a ferromagnetic one. It is vise versa for the system (
) acts like antiferromagnetic system than a ferromagnetic one. It is vise versa for the system (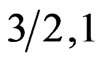 ). Although this form delays the appearance of antiferromagnetic mode but the general behavior of the system remains unchanged. As a conclusion, we found an agreement with earlier calculations that the system with
). Although this form delays the appearance of antiferromagnetic mode but the general behavior of the system remains unchanged. As a conclusion, we found an agreement with earlier calculations that the system with 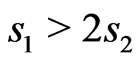 is more ferromagnetic and the system with
is more ferromagnetic and the system with 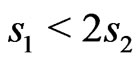 is more antiferromagnetic.
is more antiferromagnetic.
Specific heat shows the same different behavior with dimerization. Shocttky-like peak at intermediate temperature shifts towards larger values of T. That means: the antiferromagnetic excitation mode, which plays a major rule to this peak, goes to a little higher temperature before it become predominant with the increase of dimerization. While at low temperature dimerization suppresses the specific heat, 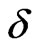 pushes it up at intermediate T for higher values of dimerization.
pushes it up at intermediate T for higher values of dimerization.
2.2. Frustrated Ferrimagnetic Chain with δ = 0
The effect of frustration in ferrimagnetic systems was investigated [2,21] at zero temperature. Several characterization of the frustration parameter were reported; mainly, 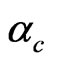 which marks the complete destruction of the long range order in the system and
which marks the complete destruction of the long range order in the system and 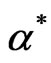 marks the onset of spiral phase transition. At any finite temperature, we found that they are temperature independent. We will study the thermal effect of a frustrated chain in the absence of dimerization.
marks the onset of spiral phase transition. At any finite temperature, we found that they are temperature independent. We will study the thermal effect of a frustrated chain in the absence of dimerization.
Free energy decreases with frustration. This decrease is faster for higher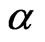 , and scales with T as
, and scales with T as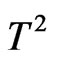 . At the critical value of frustration,
. At the critical value of frustration, 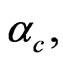 the free energy become imaginary and our LSW theory fails to go beyond this value of frustration. It was reported earlier [2,21] that at T = 0.0 the ground states energy increases with frustration parameter and then starts to decrease for values of frustration close to
the free energy become imaginary and our LSW theory fails to go beyond this value of frustration. It was reported earlier [2,21] that at T = 0.0 the ground states energy increases with frustration parameter and then starts to decrease for values of frustration close to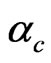 .
.
Like the dimerization effect in ferrimagnetic chains, the total magnetization of the system decreases with increasing temperature and frustration. At 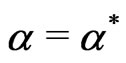 we found that the reduction on magnetization is faster because of phase transition at this point.
we found that the reduction on magnetization is faster because of phase transition at this point.
The shocttky-like peak at intermediate temperatures is also observed in the specific heat with frustration. Frustration enhances antiferromagnetic mode by causing the peak to shift to lower values of temperature. Below this maximum, 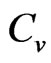 is suppressed with the increase of frustration parameter
is suppressed with the increase of frustration parameter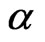 .
.
Susceptibility time temperature decreases at small 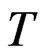 to a minimum after which it starts to increase for the three spin systems. As in the case of Schottky-like peak in specific heat, frustration makes this minimum in
to a minimum after which it starts to increase for the three spin systems. As in the case of Schottky-like peak in specific heat, frustration makes this minimum in 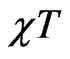 to shift towards smaller values of T verifying the enhancment of antiferromagnetic excitation mode due to frustration and it also pushes the
to shift towards smaller values of T verifying the enhancment of antiferromagnetic excitation mode due to frustration and it also pushes the 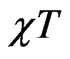 to higher values for larger values of
to higher values for larger values of 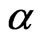 after the minimum. The slope after the minimum varies form spin system to another and shows an agreement with the previous conclusion: the spin system (
after the minimum. The slope after the minimum varies form spin system to another and shows an agreement with the previous conclusion: the spin system (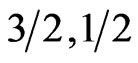 ) shows antiferromagnetic aspect more than a ferromagnetic one and the system (
) shows antiferromagnetic aspect more than a ferromagnetic one and the system (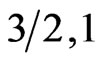 ) is more ferromagnetic than antiferromagnetic one.
) is more ferromagnetic than antiferromagnetic one.
3. Frustration on a Square Lattice
In a two-dimensional lattice, different phonons produce different types of dimerizations. A lattice distortion that involves two phonons, one with wavevector (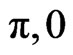 ) the other with wavevector (
) the other with wavevector (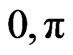 ), forming a plaquette lattice, was found to be the most favored one [14,22,23]. We will restrict our investigation to this kind of dimerization.
), forming a plaquette lattice, was found to be the most favored one [14,22,23]. We will restrict our investigation to this kind of dimerization.
Using the untruncated exchange coupling defined in Equation (2) for both nearest neighbor and the next nearest neighbor interactions, the Hamiltonian of a ferrimagnetic square lattice can be written as a sum of the nearest neighbor and the next nearest neighbor parts:
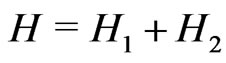 (9)
(9)
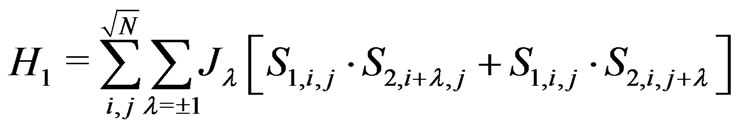 (10)
(10)
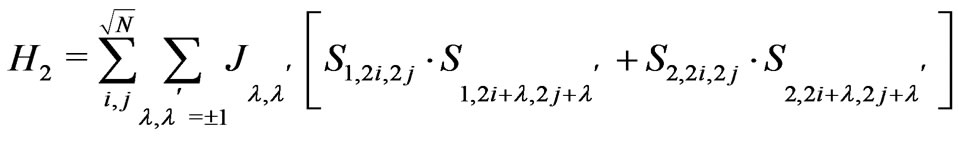 (11)
(11)
with
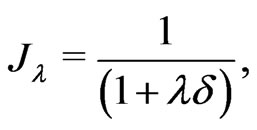 and
and
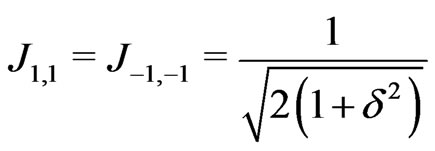 (12)
(12)
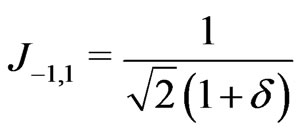 (13)
(13)
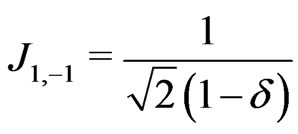 (14)
(14)
Using HP transformation and Bouglibove tansformation the above Hamiltonian can be diagonalized. The procedure of working out the physical quantities was discussed in detail in Ref. [2]. After that all the thermal quantities defined above are reproducible for the case of 2D.
3.1. Dimerization in a Non-Frustrated Square Lattice
Like in the chain, free energy and total magnetizationdefined in Equations (4) and (8) respectively, were founded to decrease with increasing temperature as shown for the system 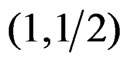 in Figures 1 and 2 respectively. This is true regardless the magnitude values of spins
in Figures 1 and 2 respectively. This is true regardless the magnitude values of spins 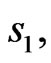 and
and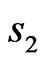 . At T = 0 the free energy reduces [13,14] to the zero temperature ground state energy. We found that the decrease in both goes as
. At T = 0 the free energy reduces [13,14] to the zero temperature ground state energy. We found that the decrease in both goes as 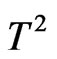 in the three spin systems. Along with temperature, we found that dimerization suppress free energy with larger values of
in the three spin systems. Along with temperature, we found that dimerization suppress free energy with larger values of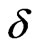 , while it increases the total magnetization at a fixed value of T.
, while it increases the total magnetization at a fixed value of T.
Specific heat shows a shocttky-like peak at intermediate temperatures. At low temperature specific heat goes as 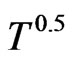 This peak is softening with increasing of dimerization parameter and shifts towards higher values of temperature. While at low temperature, say below the peak temperature, dimerization reduces the specific heat,
This peak is softening with increasing of dimerization parameter and shifts towards higher values of temperature. While at low temperature, say below the peak temperature, dimerization reduces the specific heat, 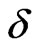 enhances specific heat at intermediate T as shown in Figure 3 for the case of spin
enhances specific heat at intermediate T as shown in Figure 3 for the case of spin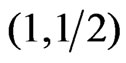 . The double peak is observed, not for the system
. The double peak is observed, not for the system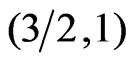 , at least within our T range, which suggests that even at a high values of
, at least within our T range, which suggests that even at a high values of
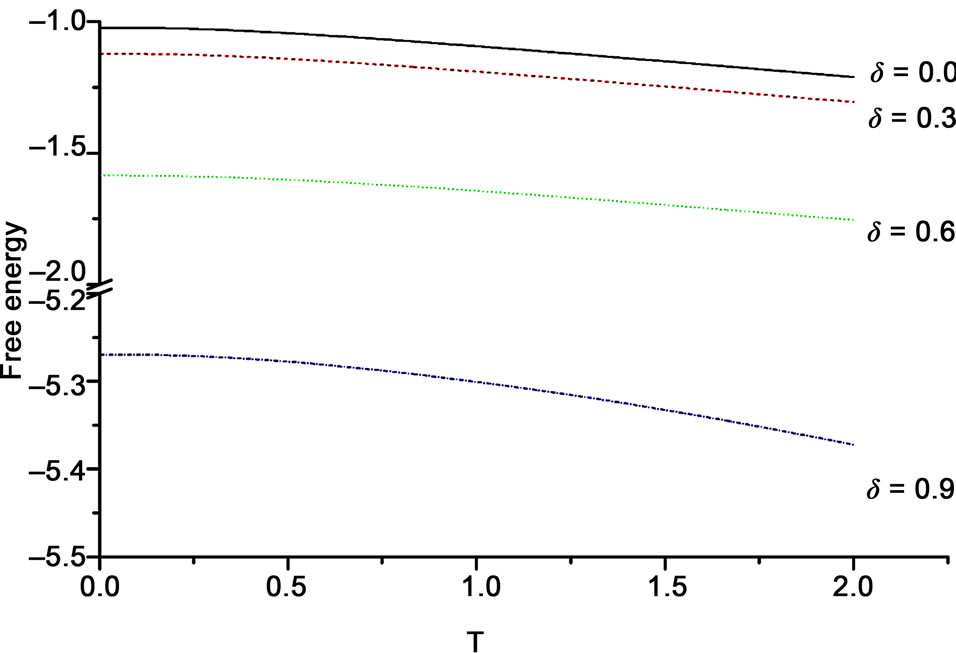
Figure 1. The free energy of a square lattice (1, 1/2) ferrimagnet vs T for different values of δ.
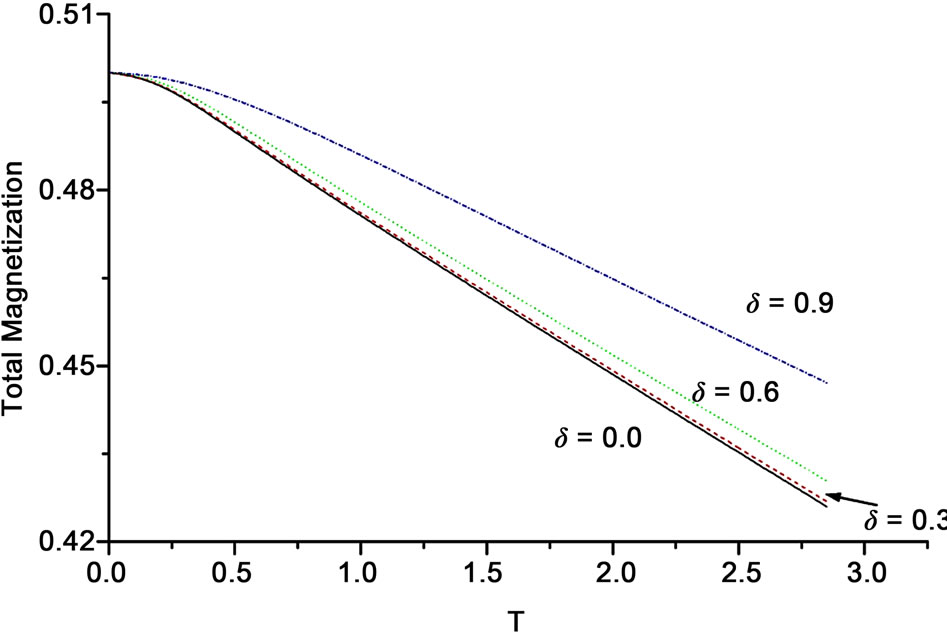
Figure 2. The total magnetization as a function of temperature in 2D (1, 1/2) system for different values of δ.
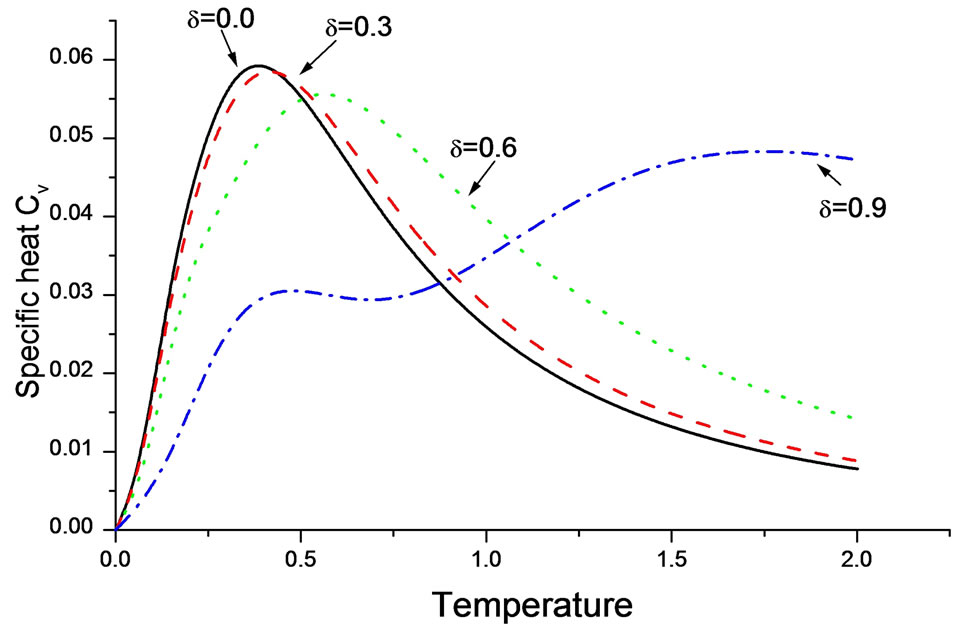
Figure 3. The specific heat of a square lattice with spin system (1, 1/2) against T in the presence of dimerization.
dimerization there is still a gapped and pagless modes in the systems. The above result again shows that the antiferromagnetic aspect is predominant in the case of intermediate temperature.
The susceptibility times temperature was also obtained using the Equation (5) for the square lattice. At zero dimerization it was reported by Yoshihiro et al. [24] that the uniform susceptibility shows an increasing behavior with temperature; although his diagrams started at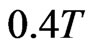 , which we found there is a decrease before this increase as shall be discussed below.
, which we found there is a decrease before this increase as shall be discussed below.
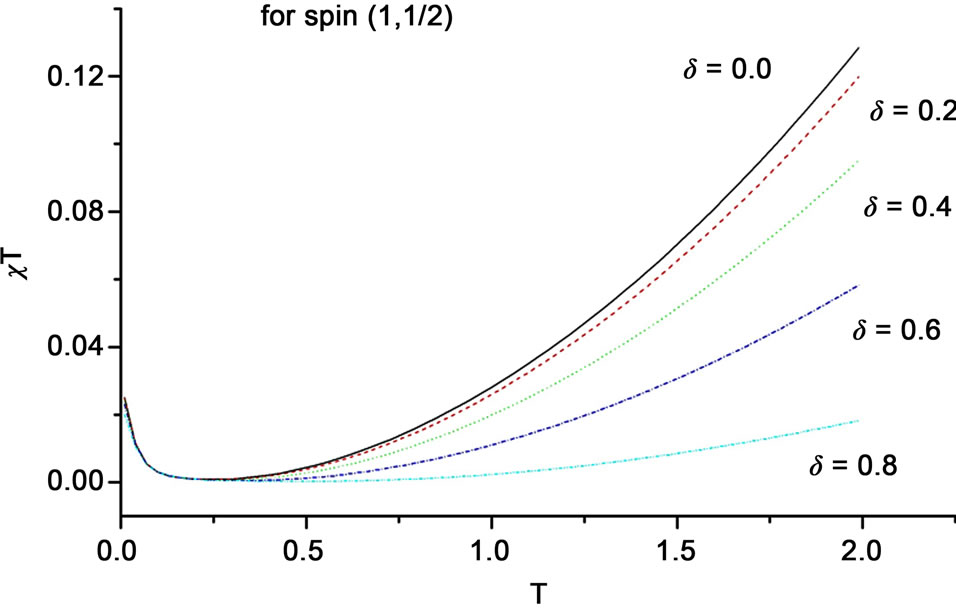
We found that in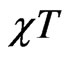 , the ferromagnetic mode smeared out at T much earlier than the case of chains. The minimum, in support to the specific heat observations, shifts toward higher temperature, and after the minimum,
, the ferromagnetic mode smeared out at T much earlier than the case of chains. The minimum, in support to the specific heat observations, shifts toward higher temperature, and after the minimum, 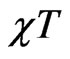 further suppressed with the increase of dimerization parameter. This behavior is observed in the three spin systems and illustrated in Figure 4. From the slope of
further suppressed with the increase of dimerization parameter. This behavior is observed in the three spin systems and illustrated in Figure 4. From the slope of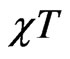 , for different
, for different 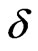 values after this minimum, we found that even in 2D the system with
values after this minimum, we found that even in 2D the system with 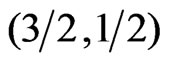 shows antiferromagnetic behavior more than ferromagnetic and it is vis versa for the spin system (
shows antiferromagnetic behavior more than ferromagnetic and it is vis versa for the spin system (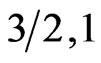 ) as clear from Figure 4.
) as clear from Figure 4.
 (a)
(a)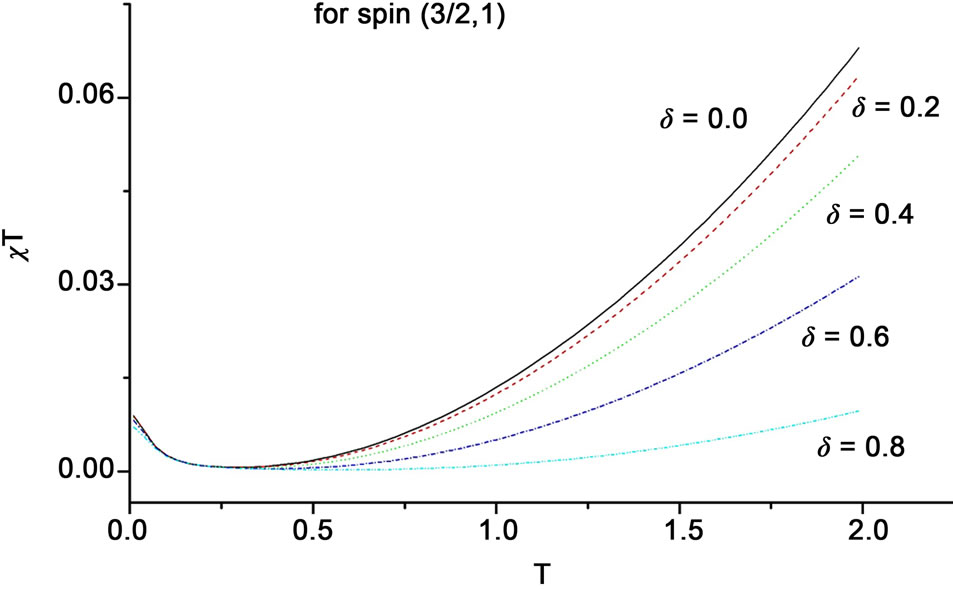 (b)
(b)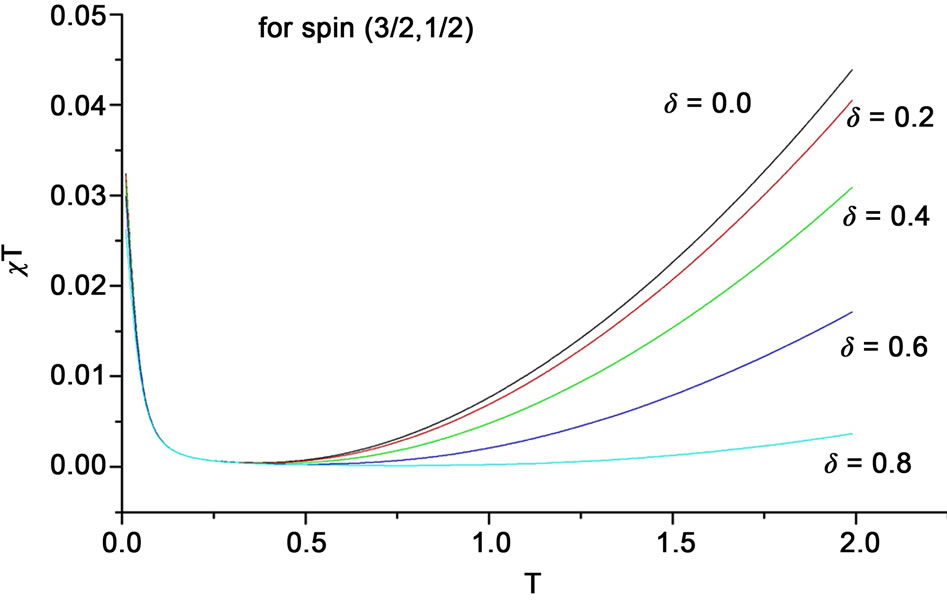 (c)
(c)
Figure 4. The behavior of χT vs T for several values on dimerization parameter shown for: (a) for the spin system (1, 1/2); (b) for (3/2, 1); and (c) for (3/2, 1/2).
3.2. Zero Dimerization in Frustrated 2D Ferrimagnetic Lattice
The free energy found to decrease with increasing frustration and also scales with T as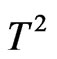 . While temperature decreases the free energy it got increased with frustration parameter. This behavior is illustrated in Figure 5 for the case of spin
. While temperature decreases the free energy it got increased with frustration parameter. This behavior is illustrated in Figure 5 for the case of spin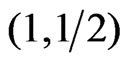 .
.
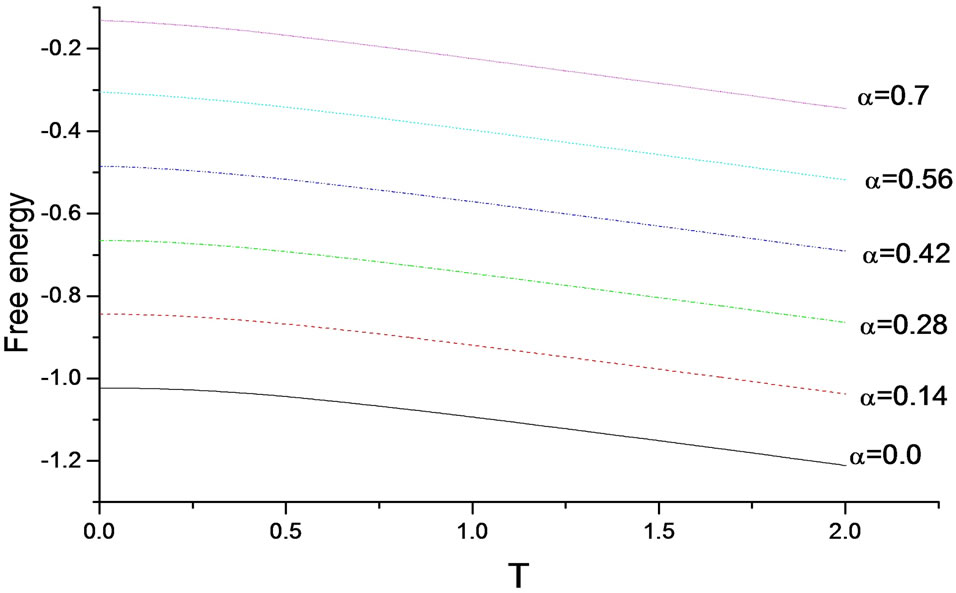
Figure 5. The free energy of a square lattice (1, 1/2) ferrimagnet vs T for different values of α.
Total magnetization shows a decrease with frustration and temperature. This decrease goes with T as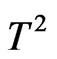 . Unlike the case of free energy, frustration increases the reduction in total magnetization as a function of temperature until it reaches the transition value
. Unlike the case of free energy, frustration increases the reduction in total magnetization as a function of temperature until it reaches the transition value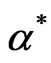 , which after it will make a jump to higher values of magnetization and then starts again to decrease with increasing
, which after it will make a jump to higher values of magnetization and then starts again to decrease with increasing 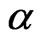 as clear from Figure 6.
as clear from Figure 6.
Specific heat shows a shocttky-like peak at intermediate temperatures for different values of frustration. While dimerization at low temperatures reduces the specific heat, frustration push it up. At intermediate T, frustration decreases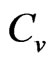 . The shocttky-like peak reduced in height with frustration and shifts towards smaller values of temperatures as can be seen from Figure 7. A double peak is observed in the three spin systems.
. The shocttky-like peak reduced in height with frustration and shifts towards smaller values of temperatures as can be seen from Figure 7. A double peak is observed in the three spin systems.
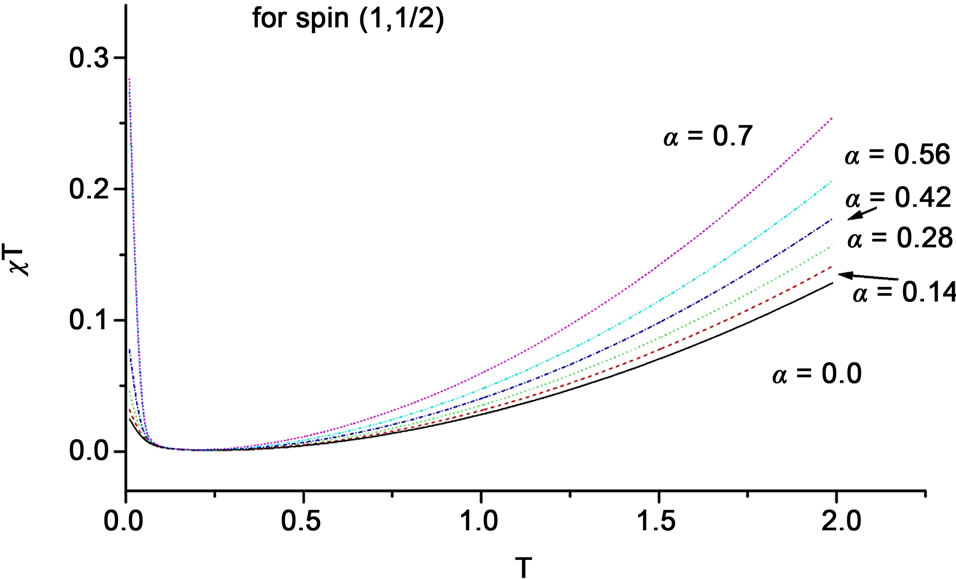
As shown in Figure 8, 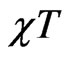 shows a minimum which shifts towards smaller T by introducing more frustration in the system indicating that frustration supports the enhancment of antiferromagnetic mode in these systems. After this minimum frustration increases the susceptibility. From this increase we reach to the same conclusion
shows a minimum which shifts towards smaller T by introducing more frustration in the system indicating that frustration supports the enhancment of antiferromagnetic mode in these systems. After this minimum frustration increases the susceptibility. From this increase we reach to the same conclusion
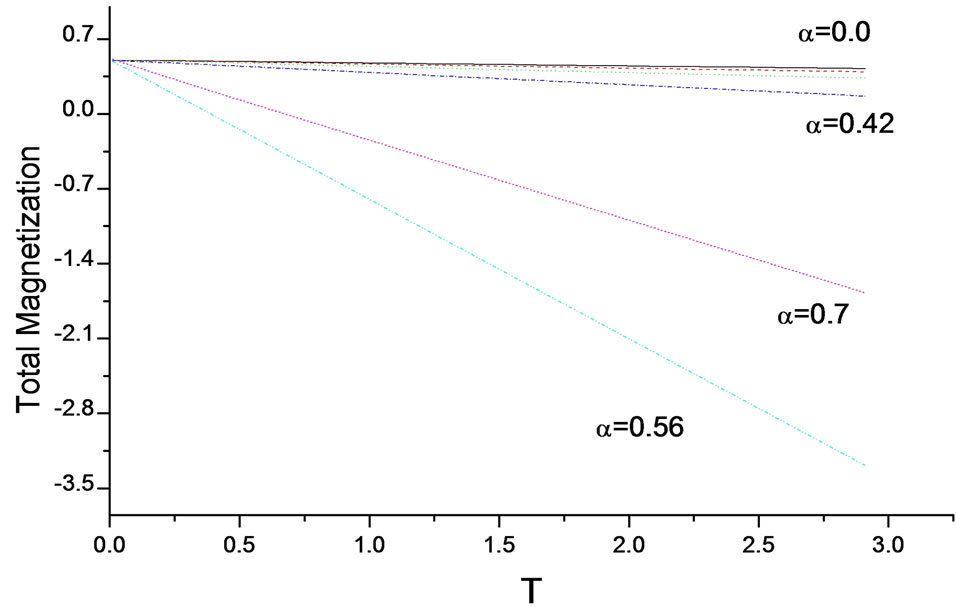
Figure 6. The total magnetization as a function of temperature in 2D (1, 1/2) system for different values of α.
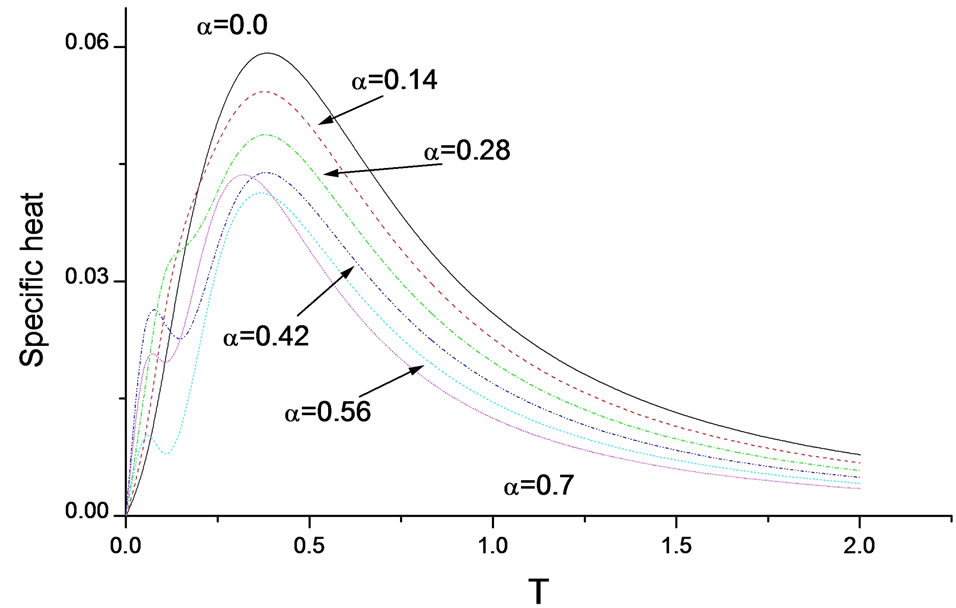
Figure 7. The specific heat of a square lattice with spin system (1, 1/2) against  in the presence of frustration.
in the presence of frustration.
 (a)
(a)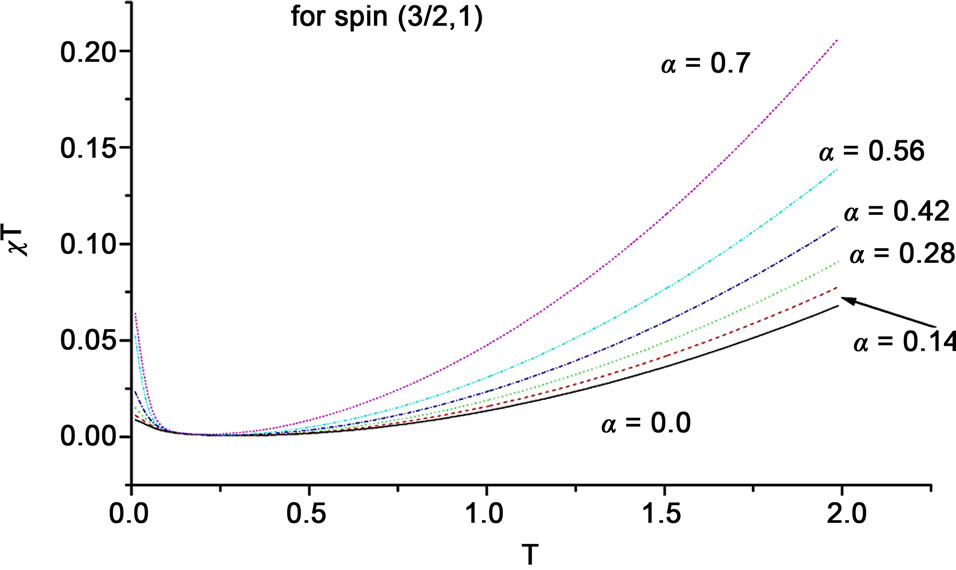 (b)
(b)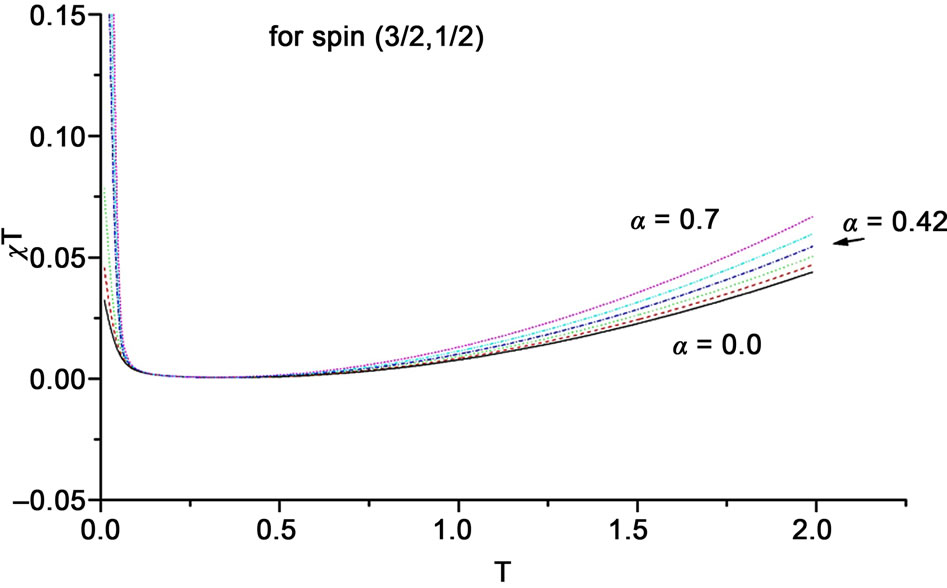 (c)
(c)
Figure 8. The behavior of χT vs T for several values on frustration parameter shown for: (a) for the spin system (1, 1/2), (b) for (3/2, 1) and (c) for (3/2, 1/2).
that in a square ferrimagnetic lattice the spin system 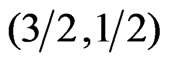 shows antiferromagnetic behavior more than ferromagnetic and it is vis versa for the spin system (
shows antiferromagnetic behavior more than ferromagnetic and it is vis versa for the spin system (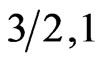 ).
).
In summery we have used linear spin wave theory to study the thermal properties of ferrimagnetic system in the presence of frustration as well as dimerization parameters. In a chain, we found that dimerization enhances the antiferromagnetic aspect by taking coupling constat as 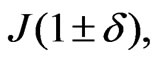 it delays the mode in the case of
it delays the mode in the case of 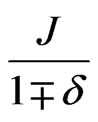 . In chains as well as in square lattices we found that the spin system
. In chains as well as in square lattices we found that the spin system 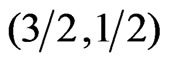 shows antiferromagnetic behavior more than ferromagnetic and the spin system (
shows antiferromagnetic behavior more than ferromagnetic and the spin system (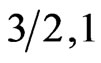 ) has a ferromagnetic one more than the antiferromagnetic aspect. We also found that both magnetization and free energy get decreased with frustration as well as dimerization and scales to square low of behavior with T.
) has a ferromagnetic one more than the antiferromagnetic aspect. We also found that both magnetization and free energy get decreased with frustration as well as dimerization and scales to square low of behavior with T.
REFERENCES
- H. J. De Vega and F. Woynarivich, “New Integrable Quantum Chains Combining Different Kinds of Spins,” Journal of Physics A, Vol. 25, No. 17, 1992, p. 4499. doi:10.1088/0305-4470/25/17/012
- A. Al-Omari and A. H. Nayyar, “Dimerization of Ferrimagnets on Chains and Square Lattices,” Journal of Physics: Condfensed Matter, Vol. 11, No. 2, 1999, p. 465. doi:10.1088/0953-8984/11/2/012
- S. K. Pati, S. Remasesha and D. Sen, “Low-Lying Excited States and Low-Temperature Properties of an Alternating Spin-1-Spin-1/2 Chain: A Density-Matrix Renormalization-Group Study,” Physical Review B, Vol. 55, No. 14, 1997, p. 8894.
- S. K. Pati, S. Ramasesha and D. Sen, “A Density Matrix Renormalization Group Study of LowEnergy Excitations and Low-Temperature Properties of Alternating Spin Systems,” Journal of Physics: Condfensed Matter, Vol. 9, No. 41, 1997, p. 8707. doi:10.1088/0953-8984/9/41/016
- C. Wu, B. Chen, X. Dai, Y. Yu and Z.-B. Su, “Schwinger-Boson Mean-Field Theory of the Heisenberg Ferrimagnetic Spin Chain,” Physical Review B, Vol. 60, No. 2, 1999, pp. 1057-1063. doi:10.1103/PhysRevB.60.1057
- S. Yamamoto and T. Fukui, “Thermodynamic Properties of Heisenberg Ferrimagnetic Spin Chains: Ferromagnetic-Antiferromagnetic Crossover,” Physical Review B, Vol. 57, No. 22, 1998, pp. 14008-14011. doi:10.1103/PhysRevB.57.R14008
- S. Yamamoto, T. Fukui, K. Maisinger and U. Schollowock, “Combination of Ferromagnetic and Antiferromagnetic Features in Heisenberg Ferrimagnets,” Journal of Physics: Condfensed Matter, Vol. 10, No. 48, 1998, p. 11033. doi:10.1088/0953-8984/10/48/023
- S. Yamamoto and T. Sakai, “Low-Energy Structure of Heisenberg Ferrimagnetic Spin Chains,” Journal of the Physical Society of Japan, Vol. 67, 1998, pp. 3711-3714. doi:10.1143/JPSJ.67.3711
- S.-S. Gong, W. Li, Y. Zhao and G. Su, “Magnetism and Thermodynamics of Spin-(1/2, 1) Decorated Heisenberg Chain with Spin-1 Pendants,” Physical Review B, Vol. 81, No. 21, 2010, pp. 214431-214439. doi:10.1103/PhysRevB.81.214431
- N. B. Ivanov, “Spin Models of Quasi-1D Quantum Ferrimagnets with Competing Interactions,” Condensed Matter Physics, Vol. 12, No. 3, 2009, pp. 435-447. doi:10.5488/CMP.12.3.435
- W Selke and J. Oitmaa, “Monte Carlo Study of MixedSpin S = (1/2, 1) Ising Ferrimagnets,” Journal of Physics: Condfensed Matter, Vol. 22, No. 7, 2010, p. 76004. doi:10.1088/0953-8984/22/7/076004
- T. Sarkar, V. Pralong, V. Caignaert and B. Raveau, “Competition between Ferrimagnetism and Magnetic Frustration in Zinc Substituted YBaFe4O7,” Chemistry of Materials, Vol. 22, No. 9, 2010, p. 2885.
- A. Winkler, N. Narayanan, D. Mikhailova, K. G. Bramnik, H. Ehrenberg, H. Fuess, G. Vaitheeswaran, V. Kanchana, F. Wilhelm, A. Rogalev, A. Kolchinskaya and L. Alff, “Magnetism in Re-Based Ferrimagnetic Double Perovskites,” New Journal of Physics, Vol. 11, No. 7, 2009, p. 73047. doi:10.1088/1367-2630/11/7/073047
- M. Takahashi, “Modified Spin-Wave Theory of a SquareLattice Antiferromagnet,” Physical Review B, Vol. 40, No. 2, 1989, pp. 2494-2501. doi:10.1103/PhysRevB.40.2494
- Aiman Al-Omari, “Thermal Properties of Ferrimagnetic Systems,” Accepted for Publication in World Journal of Condensed Matter Physics, August 2011.
- A. Al-Omari and A. H. Nayyar, “The Combined Effect of Frustration and Dimerization in Ferrimagnetic Chains and Square Lattices,” Journal of Physics: Condfensed Matter, Vol. 12, No. 48, 2000, p. 9949. doi:10.1088/0953-8984/12/48/311
- S. Yamamoto, “Magnetic Properties of Quantum Ferrimagnetic Spin Chains,” Physical Review B, Vol. 59, No. 2, 1999, pp. 1024-1027. doi:10.1103/PhysRevB.59.1024
- M. Hagirwara, K. Minami, Y. Narumi, K. Tatani and K. Kindo, “Magnetic Properties of a Quantum Ferrimagnet: NiCu(pba)(D2O)3·2D2O,” Journal of the Physical Society of Japan, Vol. 67, 1998, pp. 2209-2211. doi:10.1143/JPSJ.67.2209
- S. Yamamoto, T. Fukui and T. Sakai, “Characterization of Ferrimagnetic Heisenberg Chains According to the Constituent Spins,” The European Physical Journal B, Vol. 15, No. 21, 2000, pp. 211-219. doi:10.1007/s100510051118
- K. Maisinger, U. Schollwöck, S. Brehmer, H.-J. Mikeska, and S. Yamamoto, “Thermodynamics of the (1, 1/2) Ferrimagnet in Finite Magnetic Fields,” Physical Review B, Vol. 58, No. 10, 1998, pp. 5908-5911. doi:10.1103/PhysRevB.58.R5908
- N. Ivanov, J. Richter and U. Schollwock, “Frustrated Quantum Heisenberg Ferrimagnetic Chains,” Physical Review B, Vol. 58, No. 21, 1998, pp. 14456-14461. doi:10.1103/PhysRevB.58.14456
- S. Tang and J. E. Hirsch, “Peierls Instability in the TwoDimensional Half-Filled Hubbard Model,” Physical Review B, Vol. 37, No. 16, 1988, pp. 9546-9558. doi:10.1103/PhysRevB.37.9546
- A. Feiguin, C. J. Gazza, A. E. Trumper and H. A. Ceccatto, “Spin-Peierls Dimerization and Frustration in TwoDimensional Antiferromagnets,” Journal of Physics: Condfensed Matter, Vol. 6 No. 34, 1994, p. 503. doi:10.1088/0953-8984/6/34/002
- Y. Takushima, A. Koga and N.Kawakami, “Magnetic Double Structure for S = 1 and S = 1/2 Mixed-Spin Systems,” Physical Review B, Vol. 61, No. 22, 2000, pp. 15189-15195. doi:10.1103/PhysRevB.61.15189

