ABSTRACT

The main goal of this work is a feasibility study for the Bayesian Processor of Output (BPO) method applied to tropical convective precipitation regimes over Central and West Africa. The study uses outputs from the Weather Research and Forecasting (WRF) model to develop and test the BPO technique. The model ran from June 01 to September 30 of 2010 and 2011. The BPO method is applied in each grid point and then in each climatic zone. Prior (climatic) distribution function is estimated from the Tropical Rainfall Measuring Mission (TRMM) data for the period 2002-2011. Many distribution functions have been tested for the fitting. Weibull distribution is found to be a suitable fitting function as shown by goodness of fit (gof) test in both cases. The rain pattern increases with the value of the probability p. BPO method noticeably improves the distribution of precipitation as shown by the spatial correlation coefficients. It better detects certain observed maxima compared to the raw WRF outputs. Posterior distribution (forecasting) functions allow for a simulated rainfall amount, to deduce the probability that observed rainfall falls above a given threshold. The probability of observing rainfall above a given threshold increases with simulated rainfall amounts.

Keywords:

Probabilistic Quantitative Precipitation Forecast, BPO, WRF, Weibull Distribution

1. Introduction

Economies of sub-Saharan Africa largely depend on agriculture. The agriculture is essentially rain-fed. Precipitation is the most important and most widely studied weather variable ( [1] [2] [3] [4] [5] ). Important decisions in agriculture, hydrology, aviation, event planning and other areas depend on the presence or absence of precipitation, as well as precipitation accumulation. Reliable predictions of precipitation occurrence and precipitation amount are useful for above mentioned applications.

For these reasons, there is a great deal of research activities to improve quantitative precipitation forecast (QPF) and weather centers continuously evaluate their operational high-resolution limited-area models to trace error sources. QPF is particularly challenging over Equatorial Africa, especially capturing small convective cells that constitute most of the rain events ( [6] [7] [8] ).

Furthermore, QPFs obtained from a single numerical weather prediction (NWP) model are deterministic, and thus do not convey any information about the uncertainty about the prediction, which is a shortcoming in weather-related decision-making [9] . One approach to incorporating uncertainty information into weather forecasting is via ensembles of numerical forecasts ( [10] [11] ). While this is a major advance, the use of statistical post processing techniques for numerical forecasts remains essential. Several methods have been developed to statistically post process numerical predictions of precipitation occurrence and produce probabilistic quantitative precipitation forecasts. They include linear regression ( [12] [13] [14] ), quantile regression ( [15] [16] ), logistic regression ( [17] [18] ), neural networks ( [19] [20] ), binning techniques ( [21] [22] ), hierarchical models based on climatic prior distributions [23] , and two-stage models in which a Gamma density is employed to model precipitation accumulation ( [24] [25] [26] [27] ).

In this paper, Bayesian Processor of Output for probabilistic quantitative precipitation forecasts is used. The Bayesian Processor of Output (BPO) is a theoretically-based technique for probabilistic forecasting of weather variates. It processes output from a numerical weather prediction (NWP) model and optimally fuses it with climatic data in order to quantify uncertainty about a predictand. The theoretical structures of the BPO are derived from the laws of probability theory.

As is well known, Bayes theorem provides the optimal theoretical framework for fusing information from different sources and for obtaining the probability distribution of a predictand, conditional on a realization of predictors, or conditional on an ensemble of realizations [28] .

The objective of this work is a feasibility study for the Bayesian Processor of Output (BPO) method applied to tropical convective precipitation regimes over Central and West Africa. The paper is organized as follows: In Section 2, the model and experimental design are described, followed by the data used in this study. In Section 3, BPO techniques are briefly presented followed by the verification of BPO forecasts in Section 4. In Section 5, results for probabilistic forecasts of daily precipitation accumulation over the Central and West Africa is presented. Section 6 is devoted to the conclusion.

2. Model Description and Experimental Design

2.1. Model Description

We performed simulations using version 3.3 of the Advanced Research Weather Research and Forecasting (ARW-WRF) model [29] , which is being developed by the Mesoscale and Meteorology Division of the National Center for Atmospheric Research (NCAR). The WRF model is a numerical weather prediction model designed for a wide range of applications, ranging from idealized research to operational forecasting. It is a fully compressible, Euler nonhydrostatic model, with mass-based, terrain-following hydrostatic pressure vertical coordinates and Arakawa C-grid horizontal staggering. For the current work we choose the third-order Runge-Kutta split-explicit time-integration scheme and sixth-order centered differencing for advection and prognostic variables, conserving the flux form of mass, momentum, entropy, and scalars. Previous work has been done (not shown here) to determined satisfactory configurations by testing numerous physical parameterizations. Satisfactory Physical configurations are summarized in Table 1.

Hong et al. [30] developed the single-moment six-class microphysics scheme for the WRF, which includes graupel as an additional predictive variable. This microphysics scheme was found to significantly influence the evolution of surface precipitation [30] . Also used is the rapid radiative transfert model (RRTM) [31] . The RRTM longwave scheme accounts for multiple bands, trace gases, and microphysics species. The first-order closure scheme of Yonsei University (YSU) used for the planetary boundary layer (PBL) is a non-local K scheme with an explicit entrainment layer and parabolic K profile in the unstable mixed layer. The Noah land surface model (Noah LSM) is used to calculate soil temperature and moisture. The Tiedtke convection scheme is a bulk flux convection scheme [32] . It handles three types of convection: deep, middle level, and shallow convection. In the Tiedtke scheme, only one convective cloud is considered, comprising one single saturated updraft. Entrainment and detrainment between the cloud and the environment can take place at any level between the free convection level and the zero-buoyancy level. There is also one single downdraft extending from the free sinking level to the cloud base. The mass flux at the top of the downdraft is a constant fraction of the convective mass flux at the cloud base. This downdraft is assumed to be saturated and is kept at saturation by evaporating precipitation. The original closure assumption for deep convection relies on a closure in

moisture convergence, while that used in this version is based on the convective available potential energy (CAPE) modified by [33] .

2.2. Experimental Setup

The model is run from June 01 to September 30 of 2010 and 2011. The initial and boundary conditions are provided by the National Center for Environmental Prediction (NCEP) Global Forecasting System (GFS) three hourly products. We use the 0000 UTC cycle and run the WRF model for 48 hours starting at 0000 UTC. The model is set at a horizontal grid resolution of 25 km × 25 km and has 41 vertical levels. Data analysed are total precipitation amount for the 24-hourperiod starting at 0600 UTC, thus having 6 hours of spinup (from 00 UTC to 0600 UTC).

2.3. Area of Study

The study area extends from 15˚W to 30˚E and 10˚S to 30˚N (Figure 1). A regionalization of the domain was carried out using the one-degree daily precipitation data set developed by the Global Precipitation Climatology Project (GPCP) [34] for the period 1997-2008.

Six distinct main climatic regions (Figure 2) were delineated using a Ward’s clustering technique ( [35] [36] [37] [38] [39] ). In the following, the analysis will be conducted in each of the five regions (Region 2 to Region 6) that cover the study area (See Figure 2).

Region 2 covers arid (Sahara Desert) and semiarid (Sahel) zones over Mauritania, Mali, Niger, Chad and parts of Sudan, Cameroon and Nigeria. In the northern part of this region the climate is uniformly dry, with most areas receiving less than 130 mm/year of rain, some getting none at all for some years.

The southern part serves as a transition zone between the arid Sahara and the wetter savanna region further south. Annual rainfall averages between 100 and 200 mm received from June to September (Figure 3). Region 3 covers Liberia, Ivory Coast, Ghana, Togo, Benin, Nigeria, Cameroon and Central African Republic, in the area bordering the Gulf of Guinea. It has both areas of hot dry season (moderate rainfall) and wet climate (high, all-year rainfall). Rainfall ranges between 100 and 400 mm/year in the former and as much as 1800 mm in the latter. Region 4 represents the transition between the ocean and the continent. Breeze phenomena are very recurrent. Region 5 covers the South Atlantic Ocean and represents an oceanic climate. Region 6 is characterized by the tropical wet climate.

2.4. Data Sources and Structure

2.4.1. TRMM 3B42

For the purpose of verification we used Tropical Rainfall Measuring Mission (TRMM) data as ground truth. TRMM data show that the JJAS seasons 2010 and 2011 were wet and dry respectively (Figure 4). TRMM was used instead of gauge data because of the irregular spatial distribution of gauges and the sparse network in the region. TRMM is a joint mission of the American National Aeronautics and Space Administration (NASA) and the Japanese National Space Development Agency (NASDA) to measure precipitation in the tropics and subtropics. In this work, version 6 of the 3B42 data set is used. It provides three hourly estimations of rainfall on a 0.25˚ × 0.25˚ grid. These data are provided online by the NASA at http://mirador.gsfc.nasa.gov. Nicholson et al. [40] evaluated TRMM products over West Africa over the May to September season. They found that TRMM-merged rainfall products showed excellent agreement with gauge data.

Although the 0.25˚ grid spacing of TRMM data is close to WRF’s 25 km, they were regridded in order to achieve coincidence of both grids points.

2.4.2. 1DD GPCP Precipitation Data

The 1DD GPCP data set is a 1˚ × 1˚ longitude/latitude precipitation product

from Global precipitation Climatology Project. The GPCP algorithm combines precipitation estimates from several sources, including infrared (IR) and passive microwave (PM) rain estimates, and rain gauge observations [41] . The IR data come mainly from the different Geostationary Meteorological Satellites but also from polar-orbiting satellites for high latitudes [42] . The microwave data come from the Special Sensor Microwave Imager (SSM/I) onboard the Defense Meteorological Satellite Program. The multi-satellite estimates are first adjusted towards the large-scale gauge average for each grid box, and then combined with gauge analysis using a weighted average. 1DD GPCP Precipitation data are used in the present work to subdivide the study area into subdomains and to determine seasonal cycle in each.

3. Bayesian Processor of Output Techniques

Following the ideas of Bayes, if we have a set of forecasts and past observations, we can use this prior information to improve future forecasts. Based on past couples of forecasts and observations, we can construct a model to link each forecast amount to the probability of observed amount. Example, determine the probability of observing a rainfall amount greater than 10 mm, knowing that the forecast amount is 1 mm. The concept is illustrated in Figure 5. The BPO is operationalized by the meta-Gaussian model ( [43] [44] [45] ). It is described below in terms of input elements and forecasting equations.

3.1. Input Elements

The following algorithm defines the input elements, outlines the estimation procedure, and details the calculation of the posterior parameters (the parameters of the forecasting equations).

Step 0: Given are two samples, the climatic sample of the predict and W, and the joint sample of the predictor vector and the predict and (X, W), respectively:

,

,

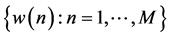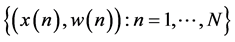where 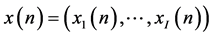and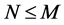; all realizations of W from the joint sample are included in the climatic sample. The index 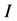scans over the number of predictors.

Step 1: Using the climatic sample, the prior (climatic) distribution function G of predict and W is estimated, such that; 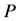denotes the probability.

Let g denote the corresponding prior (climatic) density function of W.

Step 2: Using the marginal sample 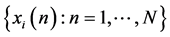of the joint sample, we estimate the marginal distribution function 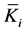of predictor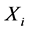, such that

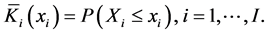
(The bar over 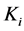signifies that this is only an initial distribution function of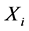, which need not cohere to the specified prior distribution function of W and the yet-to-be-constructed family of likelihood functions. This detail is accounted for in the derivation of the meta-Gaussian BPO, and thus need not be considered in application.)

Step 3: The normal quantile transform (NQT) of the predictand and of every predictor is defined:

where Q is the standard normal distribution function, and is the inverse of Q. Next, we apply the NQT to each realization in the original joint sample; specifically, for, we calculate, ; then the transformed joint sample is evaluated, where.

Step 4: Using the transformed joint sample, we estimate the following moments. For the transformed predictand,.

For every transformed predictor, ,. For and,.

The estimates of variances and covariances should be the maximum likelihood estimates (i.e., they should be calculated using N as the divisor).

Step 5: We form two I-dimensional column vectors, , the transpose of vector, which is denoted, and an symmetric matrix, with for, and for and. Next we calculate an symmetric matrix

(1)

Step 6: The values of the posterior parameters are calculated as follows:

(2)

(3)

(4)

where is an I-dimensional row vector.

3.2. Forecasting Equations

Given a prior distribution function G of predict and W and given a realization of the predictor vector, the meta-Gaussian posterior distribution function of predict and W is specified by the equation

(5)

For any number p such that, the p-probability posterior quantile of predict and W is specified by the equation

(6)

Given also a prior density function g of predict and W, the meta-Gaussian posterior density function of predict and W is specified by the equation

(7)

In the current work, one predictor is used. When there is only one predictor (I = 1), its subscript is omitted. Thus replaces, replaces, and the forecasting Equations (5)-(6) can be written

(8)

(9)

In the following, processing will be done by grid point and climatic zones.

4. Results

4.1. Processing by Grid Point

4.1.1. Prior Distribution Function

The prior distribution function G of precipitation amount W is conditional on precipitation occurrence:. It is estimated from the TRMM data for the period 2002-2011. This estimation is done at any grid point. Many distribution functions are tested for the fitting. Weibull distribution is found to be a suitable fitting function as shown by goodness of fit (gof) test (not shown here).

4.1.2. Marginal Distribution Function

The single predictor X is the estimate of the 24-h total precipitation. The marginal distribution function of is conditional on precipitation occurrence:

. It is estimated for WRF model outputs cover the period JJAS2010-2011 from the joint sample. Weibull distribution is also found to be more suitable.

4.1.3. Transformed Rain w_p

Once the five elements are specified, the transformed rain may be calculated, given any value p of the probability.

From the definition, the number p is the probability that the value of the precipitation is less than or equal to w p. In this section, the number p is simply interpreted as the probability that the rain is equal to w p. Only values of p for which the spatial distribution of precipitation is close to the observations will be presented.

Figure 6(a) represents the weather of June 10, 2010. This figure shows that the rain pattern produced by the BPO method is denser than those produced by WRF and TRMM for great values of the probability p. The algorithm used in the BPO method gives the cumulative distribution (CDF) of the rains. This is why the intensity of rainfall increases with the probability. Indeed, the chances of observing the precipitation less than 5 mm at a point are less than the chances to observe precipitation less than 10 mm at this point. In the following, p will be simply taken as the probability that the rain patterns be that shown on the maps.

BPO method introduces a noise, that is, it introduced rains in some parts of

the field, compared to observations.

For p = 0.4 (Figure 6(a)), the maximum rainfall is located on the coast of Liberia, Sierra Leone and Guinea. The intensity of rainfall in the region is about 15 mm. The TRMM observations confirm that these areas were rainy at June 10, 2010.

The observed intensity is 25 mm instead of 15 mm as forecasted by the BPO method for p = 0.4. For p = 0.45, other maxima are found over West Cameroon and northern Burkina Faso. It is generally found that when the probability p increases, the areas that have the maxima are preserved with the difference that intensity also increases. For p = 0.6, some observed maxima are located by the BPO method. These include the maximum observed on the north of the Central African Republic and the south-eastern Nigeria.

Figure 7(a) displays rainfall patterns of June 15, 2010. The field and intensity of rainfall increase with the value of the probability p. Maxima are detected by the BPO method especially for p = 0.45, 0.5, 0.55 and 0.6. The maximum observed in southern Nigeria is well reproduced by the BPO method. Intensities are in the same order for p = 0.6. This intensity is about 50 mm. For the values of p less than 0.6, these areas of maximum intensity are well detected but the intensities are underestimated. The maxima observed on the coast of Liberia, Sierra Leone, the Guinea Conakry are detected by the BPO method. The TRMM observations also show maxima rainfall in southern Central African Republic, northern Democratic Republic of Congo. These maxima were not well localized by BPO method.

Figure 8(a) shows the rains patterns of 20-07-2010. The maximum observed on the coast of Guinea Conakry is well locate for p = 0.6. Some maxima observed in southern Mali, south of Niger and central Nigeria have not been well detected by the BPO method.

Given the foregoing, it is found that BPO method introduced background noise. It provides low rainfall almost throughout the study area especially when the value of the probability p increases. This led us to subtract the average daily climatology (8.8 mm) over the entire region to get rid of this noise. Figure 6(b), Figure 7(b) and Figure 8(b) show these new maps. Figure 6(b) shows the rains patterns of 10-06-2010. This field is less dense than that of Figure 6(a). Some maxima are well captured by the BPO method. These maxima are observed on the coast of Sierra Leone, eastern Chad, the southwest coast of Cameroon and eastern Senegal. In general, withdrawal of the daily average climatology reduces the field of the rains. For some values of the probability (p = 0.55 and p = 0.6), this field is close enough observed field.

4.2. Processing by Climatic Zones

In the following, the analysis will be conducted in each of the five regions (Region 2 to Region 6) that cover the study area (see Figure 2). The following figures show prior and posterior distribution functions and prior and posterior densities.

4.2.1. Region 2

Figure 9(a) represents the prior (climatic) distribution function G and three

posterior distributions functions based on three different realizations: 1 mm, 10 mm and 25 mm of predictor X. For simulated value of 1 mm of precipitation, the probability of observing an amount less than or equal to 20 mm of rainfall at any point in the Region 2 is 0.75. This means that there is 75% chance to observe at any point of this region an amount of rain less or equal to 20 mm. We deduce that the probability of observing rainfall amount greater than 20 mm is 0.25, that is there is only 25% chance to observe rain greater than 20 mm in intensities.

For simulated value of 10 mm of rainfall, the probability of observing rainfall less than or equal to 20 mm is 0.65. That is 65% chance to observe rainfall ≤20 mm when the model simulates 10 mm of precipitation at a point. We deduce from the above that the probability of observing rainfall greater than 20 mm is 0.35.

Thus, there is 35% chance of observing rainfall intensities greater than 20 mm at a point when the model simulates 10 mm of rainfall. For a simulated value of 25 mm, the probability of observing rainfall ≤ 20 mm is 0.58, that is there is 58% of chance of observing rainfall ≤ to 20 mm when the WRF model simulates 25 mm of rainfall at a point. The probability to observe rainfall intensity greater than 20 mm is 0.42; that is 42% of chance.

Based on the above analysis, it appears that the probability of observing rainfall above a given threshold increases with simulated rainfall amounts. This result is consistent with that of Tanessong et al. [46] .

Figure 9(b) represents the prior (climatic) density function g and three posterior density functions based on three different realizations of predictor X: 1 mm, 10 mm and 25 mm. For a simulated rainfall amount of 1 mm, the most likely rainfall value that can be observed is 5 mm. This most likely value is 8 mm when simulated rainfall amount is 10 mm and becomes 12 mm for a simulated rainfall amount of 25 mm. Thus, when the simulated rainfall amount increases, the chances of observing heavy rainfall also increase. These results thus strengthen those found previously. Figure 9(b) also shows that the density decreases as the observed quantities increase, indicating that heavy rainfall events are rare and therefore difficult to predict.

4.2.2. Region 3

Figure 10(a) represents the prior (climatic) distribution function G and three posterior distributions functions based on three different realizations: 1 mm, 10 mm and 25 mm of predictor X. For simulated rainfall amount of 1 mm, the probability to observe rainfall ≤ 20 mm is 0.90, that is 90% of chances. Then the chances of observing the rainfall amounts greater than 20 mm are 10% only when simulated rainfall amount is 1 mm. For simulated rainfall amounts of 10 mm, the probability of observing rainfall ≤ 20 is 0.75 mm, for example; that is 75% chance.

Thus the probability of observing rainfall greater than 20 mm is 0.25; yielding 25% chance. For simulated rainfall amount of 25 mm, the probability of observing rainfall ≤ 20 mm is 0.7; 70% chance. The chances of observing the rainfall greater than 20 mm are 30%.

Unlike Region 2, we note that the chances of observing rainfall greater than a given threshold increase weakly when the simulated rainfall amount increase in

Region 3. This could be due to complex topography of Region 3. This region includes the Niger valley, the west highlands of Cameroon, the Adamawa Plateau of Cameroon and Mount Cameroon. The climate of this region is very diverse and complex.

Figure 10(b) represents the prior (climatic) density function g and three posterior density functions. For the simulated rainfall amount of 1 mm, the most likely value that can be observed is 4 mm with a density of 0.06. The most likely value is 7 mm for simulated rainfall amount of 10 mm. It is 10 mm when the simulated rainfall amount is 25 mm.

4.2.3. Region 4

Figure 11(a) represents the prior (climatic) distribution function G and three

posterior distributions functions. For simulated rainfall amount of 1 mm, the probability of observing less than or equal to 20 mm rainfall is 0.8; that is 80% chance.

The probability of observing rainfall amount greater than 20 mm is 0.2; 20% chance.

For simulated rainfall amount of 10 mm, the probability of observing rainfall ≤ 20 mm is 0.6; that is 60% chance. The probability to observe rainfall amount greater than 20 mm is 0.4. The probability of observing rainfall amounts ≤ 20 mm knowing that the simulated rainfall amount is 25 mm is 0.5 and the probability to observe rainfall greater than 20 mm is 0.5. Figure 11(b) shows that the most likely values of rainfall knowing that the simulated quantities for 1 mm, 5 mm and 25 mm are respectively 5 mm, 12 mm and 15 mm.

4.2.4. Region 5

Figure 12(a) represents the prior (climatic) distribution function G and three posterior distributions functions. The probability of observing rainfall ≤ 10 mm for example knowing that the simulated quantity is 1 mm is 0.85; 85% chance. When the simulated quantities are 10 mm and 25 mm, the probability of observing rainfall ≤ 10 mm are 0.75and 0.72 respectively. The probability of observing rainfall amounts greater than 10 mm are 0.25 and 0.28 respectively. Figure 12(b) shows that the most likely values which can be observed are between 3 and 5 mm for simulated rainfall amounts greater than 1 mm. It is noted that the most likely precipitations have low intensities. That means that heavy rainfalls are not recorded in the ocean during the JJAS season.

4.2.5. Region 6

For simulated rainfall amount of 1 mm, the probability of observing rainfall ≤ 20 mm is 0.8 and that to observe rainfall greater than 20 mm is 0.2 (see Figure 13(a)). When the simulated rainfall amounts are 10 mm and 25 mm, the probability of observing rainfall ≤ 20 mm are respectively 0.7 and 0.65 and those to observe rainfall greater than 20 mm are respectively 0.3 and 0.35. The most likely values of rainfall are 6 mm, 9 mm and 12 mm for simulated rainfall amounts of 1 mm, 10 mm and 25 mm respectively (see Figure 13(b)).

5. Conclusion

The Bayesian Processor of Output method was used to produce Probabilistic Quantitative Precipitation Forecast over Central and West Africa. It processes output from a NWP model and optimally fuses it with climatic data in order to quantify uncertainty about a predictand. Outputs from the Weather Research and Forecasting (WRF) model were used to develop and test the BPO technique. The model ran from June 01 to September 30 of 2010 and 2011. The BPO method was applied in each grid point and then in each climatic zones. Prior (climatic) distribution function was estimated from the Tropical Rainfall Measuring Mission (TRMM) data for the period 2002-2011. Many distribution functions have been tested for the fitting. Weibull distribution was found to be a

suitable fitting function as shown by goodness of fit (gof) test in both cases. BPO method noticeably improves the distribution of precipitation as shown by the spatial correlation coefficients, reliability diagrams and relative operating cha-

racteristic curves. It better detects certain observed maxima compared to the raw WRF outputs. Posterior distribution (forecasting) functions allow for a simulated rainfall amount, to deduce the probability that observed rainfall falls above a given threshold. The probability of observing rainfall above a given threshold increases with simulated rainfall amounts. The forecasting functions determined in the present paper can be used by forecasters as guidance for issuing probabilistic forecasts from a single deterministic forecast. In addition, this forecasting tool might assist forecasters throughout the season in a wide variety of weather events.

Acknowledgements

WRF simulations were done on a workstation provided by Dr Serge Janicot of LOCEAN (Paris), in the framework of the PICREVAT project, funded by the French government. WRF was provided by the University Corporation for Atmospheric Research website (for more information see http://www2.mmm.ucar.edu/wrf/users/download/get_source.html). GPCP data were obtained from the NOAA website http://www.esrl.noaa.gov. TRMM data were provided online by NASA at http://mirador.gsfc.nasa.gov.

Cite this paper

Tanessong, R.S., Vondou, D.A., Igri, P.M. and Kamga, F.M. (2017) Bayesian Processor of Output for Probabilistic Quantitative Precipitation Forecast over Central and West Africa. Atmospheric and Climate Sciences, 7, 263- 286. http://dx.doi.org/10.4236/acs.2017.73019

References