ABSTRACT

The role of phoretic forces in providing in-cloud and below-cloud scavenging due to falling drop is reviewed by considering published papers dealing with theoretical models, laboratory and field measurements. Theoretical analyses agree that Brownian diffusion appears to dominate drop scavenging of aerosol with radius less than 0.1 μm, and inertial impaction dominates scavenging of aerosol with radius higher than 1 μm. Thus, there is a minimum collection efficiency for particles in the approximate range 0.1 μm - 1 μm, where phoretic forces are felt. Generally speaking, published papers report not uniform evaluations of the contribution of thermoand diffusiophoretic forces. This disagreement is partially due to the different laboratory and field conditions, and different theoretical approaches.

1. Introduction

Aerosol particles are removed from the atmosphere by dry and wet deposition. Dry deposition directly transports aerosol particles to the Earth’ surface without the aid of precipitation. In the process of wet deposition, particles first have to be incorporated in hydrometeors and then delivered to the surface in aqueous form (rain, snow, hail or fog). Both mechanisms are strongly sizedependent, with the removal rates of aerosol from the atmosphere differing by several orders of magnitude for different particle sizes. Consequently, large particles usually deposit in areas close to sources, whereas small particles, especially sub-micron particles, can be transported far from the sources.

Wet removal (or precipitation scavenging) of aerosol particles from the atmosphere are usually split into two categories: in-cloud scavenging (wash-out) and belowcloud scavenging (rain-out). Below cloud scavenging is the process of aerosol removal from the atmosphere which occurs between cloud base and ground due to precipitation. In-cloud scavenging includes contributions from both nucleation and impaction scavenging [1,2].

In-cloud nucleation scavenging hinges on the fact that drops and ice crystals in atmospheric clouds prevalently require, for their formation, the presence of aerosol particles, called cloud condensation nuclei and ice nuclei. As a consequence, a significant portion of in-cloud aerosol particles are removed through the heterogeneous nucleation [1].

In addition to in-cloud aerosol removal due to this phase-change mechanism, aerosol particles may become scavenged inand below-cloud by water drops and ice crystals via impaction scavenging, which includes inertial impaction, Brownian diffusion, thermophoresis, diffusiophoresis, and, in the presence of charges, electric effects.

Thermophoresis is the phenomenon whereby a small particle suspended in a gas with a temperature gradient, experiences a force, called thermophoretic force. Particles move towards the region of lower temperature. The diffusiophoretic force on a particle is the sum of the force due to the gas momentum transfer process (pure diffusiophoresis) and Stefan flow, the hydrodynamic flow necessary to maintain a uniform total pressure when water vapour is diffusing through an inert resting gas [3].

In the case of pure diffusiophoresis in a binary mixture in a steady condition, the aerosol particle should move in the direction of the diffusive flux of the heavier gas molecules (e.g. air), and in the case of diffusiophoresis with Stefan flow, the direction of motion of the particulate is the same as that of the water vapour flux [4].

In clouds or during fall of hydrometeors, when growth or evaporation of droplets and ice crystals occur, there is the simultaneous presence of thermoand diffusiophoretic forces. Examples of this process are: 1) the formation of wave clouds, in which in a first step the water vapour condenses to form supercooled liquid droplets, and afterwards droplets freeze via both homogeneous or heterogeneous nucleation processes, forming a mixedphase region followed by a glaciated cloud region; 2) air entrainment at the edges of cloud, which favours the evaporation of droplets, causing a temperature gradient and water vapour density gradient from the droplet surface to the environment, so that thermophoresis and diffusiophoresis take place; 3) mixed clouds, where ice crystal and supercooled droplets initially coexist, frequently evolving toward clouds made of ice crystals only.

The aim of this paper is to review theoretical model, laboratory and field studies, which take into account the phoretic forces in the atmospheric scavenging process due to drops.

2. Theoretical Model

In-cloud scavenging is the main removal mechanisms for sub-micron particles, which are usually less efficiently removed from the atmosphere by either below-cloud scavenging or dry deposition [5,6].

Below cloud scavenging of particles is represented by a scavenging coefficient defined as:

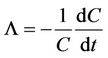
where C is the number or mass concentration of interstitial particles and t is the time.

Since most of the aerosol number is associated with small particles, while most mass is associated with large particles, L is expected to be different for the bulk number concentration and the bulk mass concentration. Generally speaking, L depends on drop and aerosol size distribution, terminal velocity of drops and aerosol particles, and drop-particle collision efficiency, a parameter that is controlled by mechanisms involving microphysical interactions between particles and hydrometeors. Such mechanisms include Brownian diffusion, inertial impaction, interception, thermophoresis, diffusiophoresis, electrostatic attraction, and airflow turbulence [1].

Many theoretical studies on scavenging phenomena do not take into account phoretic forces, either in-cloud [7- 10] or below-cloud [6,11-25], while other authors consider also phoretic scavenging mechanisms [26-34].

Studies that do not consider thermophoresis, diffusiophoresis and electric charge are likely to be inaccurate with regard to the collision efficiency and the scavenging coefficient, since they include only a sub-set of the mechanism influencing particle collection by drops.

Theoretical models agree that Brownian diffusion appears to dominate scavenging of aerosol in the size range r < 0.1 μm (r is the radius of the aerosol particles), while inertial impaction dominates scavenging in the size range r > 1 μm. Thus, there is a minimum collection efficiency for particles in the approximate range of 0.1 μm - 1 μm, where phoretic and electric effects are felt [14,15,25,35- 38]. The exact depth, width and position of this minimum depend on the properties of the aerosols and hydrometeors, and on ambient conditions. The minimum in the collection efficiency is called “the Greenfield gap”, as Greenfield [39] was the first to determine the effects of various scavenging mechanisms combined, with the exception of phoresis.

Concerning the contribution of phoretic forces in the scavenging process, it is important to evaluate the strength of thermophoretic and diffusiophoretic forces, for assessing whether they act in the same or in the opposite direction, and in the latter case, finding which force is prevalent. The different cases depend on the actual atmospheric conditions and the aerosol particle diameter. Phoretic forces strongly depend on the thermal and water vapour concentration gradient between the drop surface and the ambient air.

Some theories assume a thermal equilibrium between the drop and the environment, water vapour evaporation or condensation being considered the only factor determining the temperature gradient. In this case thermophoresis and diffusiophoresis will act in opposite ways. However, in real rain events, a falling raindrop can have a different temperature from that of the ambient air due, for instance, to its origin at higher altitudes in cloud. An ice particle can fall for 1 - 2 km, depending on the initial radius, ice density and air humidity, before complete melting can occur. Therefore, the gradients of temperature and of water vapour density are higher with respect to stationary conditions and thermophoretic and diffusiophoretic forces will reinforce each other. In clouds or during the fall of hydrometeors, when growth or evaporation of droplets and ice crystals take place, there is the simultaneous presence of thermoand diffusiophoretic forces.

Thermophoretic velocity can be calculated theoretically and from experimental published data [40-43]. Concerning diffusiophoresis, in a steady state, the problem is rather more difficult, as mentioned in the introduction. In the case of pure diffusiophoresis in the binary system water-vapour/air, the aerosol particle should move in the direction of the diffusive flux of the heavier gas molecule (i.e. air), at a velocity:

(1)

Where: m_v, m_a are the molecular masses of the vapour and carrier gas, respectively; g_v, g_a are the vapour and carrier gas mole fraction, respectively; D is the mutual diffusion coefficient for the two components and Ñg_v denotes the gradient of the water vapour mole fraction [44].

Therefore, 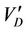depends on the gradient concentration, the molecular mass of gases, the mutual diffusion coefficient for the two components, and is independent of particle radius.

In the case of diffusiophoresis with Stefan flow, by adding the velocity 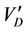to the Stefan velocity, Schmitt and Waldmann [45] obtained the following formula for the aerosol particle:

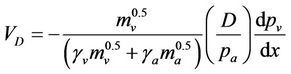(2)

where: p_a is the gas partial pressure and 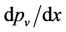is the water vapour pressure gradient. According to Goldsmith et al., [46] pure diffusiophoresis should be far less important than either Stefan flow or thermophoresis in stationary conditions. The pure diffusion should reduce the velocity expected from the Stefan flow by about 20%. Schmitt and Waldmann [45] pointed out that Equation (2) can also be applied to particles larger than the mean free path with an accuracy of about 9%.

Substituting in Equation (2) D = 0.24 cm²·s^–1 for water diffusing in air at STP and p_a = 990 mb, the following equation is obtained:

(3)

where V_D is in cm·s^–1 and the vapour pressure gradient in mb·cm^–1.

A study on the combined effect of various scavenging mechanisms was carried out by Slinn and Hales [35,47], by assuming a water drop evaporating or condensing in quasi-steady state conditions for vapour diffusion and heat conduction, which requires a slow change of the droplet radius in time. The theoretical conclusion was that thermophoresis should dominate diffusiophoresis for sub-micron particles, and that phoresis should be an important in-cloud collection mechanism. Slinn and Hales [35] also assumed that the collection kernels of the individual scavenging processes considered are additive.

In an attempt to explain the excess of ice crystals over active ice nuclei observed in several types of clouds, Young [26] suggests, following Slinn and Hales [35], that thermo-diffusiophoresis could enhance the contactfreezing nucleation process of evaporating supercooled droplets and that thermophoresis should dominate over diffusiophoresis except for aerosol with r > 1 μm.

In an attempt to improve some of the earlier approximate descriptions of particle scavenging by water drops in air, Grover et al., [29], and Wang et al., [30] computed the efficiency with which aerosol particles in the range 0.001 £ r £ 10 μm collide with water drops (range 42 μm - 438 μm) falling at terminal velocity in air, using trajectory and flux models, respectively.

The water vapour density and temperature distribution around an evaporating or condensing water drop were calculated by numerically solving the convective vapour diffusion and heat conduction equation around the drop. Phoretic effects were considered. The minimum of the collection efficiency was found in the range 0.1 μm - 2.0 μm, depending on relative humidity (r.h.) and drop size. The computation shows that the efficiency is significantly raised by phoretic forces in subsaturated air. According to this model, the collision efficiency should increase by lowering r.h., i.e. for aerosol particles with r = 0.25 μm the thermophoresis should be prevalent with respect diffusiophoresis. McGann and Jennings [48] improved the model of Grover et al., [29] and over an order of magnitude higher value was obtained for collision efficiency.

Based on Young’s conclusion, Cotton and Field [49] suggested a model of wave clouds in which the thermophoretic contribution to contact nucleation process is considered. Hoose et al., [50], in the global aerosol climate-model ECHAMS-HAM, by considering in-cloud scavenging, took into account a higher collision kernel for evaporating droplets, since thermophoresis should enhance the diffusive transport of aerosol particles towards the droplets.

Croft [34] considered below-cloud scavenging based on the collection efficiencies of Wang et al., [30], concluding that thermophoretic effects produce increases in the global and annual mean below-cloud removal of Aitken size particles of near to 15%. Considering also the contribution of thermophoresis, the below-cloud scavenging coefficient should increase from 2 × 10^–9 s^–1 to 10^–8 s^–1 by decreasing r.h. from 100% (i.e. absence of evaporation) to 50% r.h. (rain rate = 10^–2 mm·h^–1). At rain rate 1 mm·h^–1 the increase in the scavenging coefficient should be negligible.

Davenport and Peters [51] estimated the wash-out coefficients for moderate rains (1.1 mm·h^–1 to 3.0 mm·h^–1) over sampling times of 5 to 6.5 hours. The theoretical thermophoretic and diffusiophoretic scavenging was based on a large temperature difference between the air and raindrop and on vapour pressure difference corresponding to the difference in the vapour pressure of water at those temperatures, respectively. The following formula was used to evaluate the diffusiophoretic efficiency.

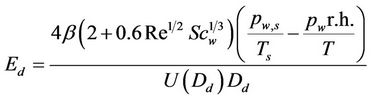(4)

where:;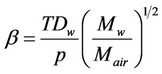

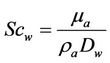
where: Re, raindrop Reynolds number; Sc_w, Schmidt number for water vapour in air; D_w, diffusivity of water vapour; ρ_a and μ_a, air density and viscosity; M_w and M_air, molecular weight of water and air; p_w,s and p_w, water vapour pressure at temperatures T_s and T;, fall velocity of raindrop with its diameter D_d; p, total air pressure; T_s, temperature of raindrop surface; T, ambient air temperature.

The efficiency shows an increase by increasing the difference between the vapour density at the drop surface and far from the drop. This should mean that, for an evaporating drop, particles move in the opposite direction of the water vapour. Therefore the formula considers only pure diffusiophoresis and does not take into account Stefan flow.

Chate [52], Andronache et al., [32], Bae et al., [33], chose the Davenport and Peters formula to evaluate the phoretic contribution, and assumed a constant difference temperature between surface drop and air, by neglecting the contribution of evaporation or condensation of water vapour to the temperature droplet. In order to interpret the data on scavenging coefficients determined from observations of ultrafine particles (with diameters in the range 0.01 μm - 0.5 μm) by Laakso et al., [53], Andronache et al., [32] developed a simplified scavenging model, which includes below-cloud scavenging processes and mixing of ultrafine particles from the boundary layer into cloud followed by cloud condensation nuclei activation, and in-cloud removal by rainfall. The raindrop size distribution described by Marshall and Palmer [54] was chosen. It is worth noting that the theoretical phoretic scavenging vs. aerosol diameter was calculated at constant temperature difference between the air and the raindrop (T_air > T_drop, in the range 0˚C - 5˚C), and at vapour pressure difference corresponding to the difference in the vapour pressure of water at those temperatures, respectively. This means that the r.h of the air was considered 100%. The increase of temperature difference resulted in a significant enhancement of the scavenging coefficient for particles in the 50 - 80 nm range. At r = 60 nm, the scavenging coefficient should increase from 6 × 10^–6 s^–1 [(T_a – T_s) = 0˚C] to 10^–5 s^–1 [(T_a – T_s = 5˚C)].

Chate [52] analyzed, both theoretically and on the basis of field measurements, the scavenging mechanisms for atmospheric aerosol removal by thunderstorm rain episodes. By considering the contribution of phoretic forces, the collision efficiency was found to increase by a factor of 5 for submicron particles, when temperature gradient varied from 1˚C to 5˚C between drop surface and ambient. It is important to evidence that in Chate’s model the drop temperature is assumed to be higher than air temperature considered at 100% r.h. Because the droplet should evaporate in such conditions, both thermophoresis and diffusiophoresis should push away the aerosol particles. Therefore, in our opinion, no scavenging should be observed due to phoretic forces in the considered conditions.

Bae et al., [33] considered the thermophoretic and diffusiophoretic contribution to the below-cloud scavenging of aerosol (range 10^–3 μm - 10² μm), by assuming a lognormal raindrop size distribution. The collection efficiency due to phoresis was evaluated, varying the air relative humidity between 50% and 90%, the ambient temperature, and the difference of temperature between air and raindrop surface (1˚C, 3˚C, 5˚C). The results of the model shown in Table 3 and Figures 4 and 5 are of the paper evidence positive scavenging coefficient for both thermophoresis and diffusiophoresis. The relative contribution of both thermophoresis and diffusiophoresis turns out to be about 80%, when particle diameter is between 0.1 and 1 μm. Examining the data reported in Tables 2 and 3 of the paper, we disagree with the conclusions of the authors. In particular, as the driving force of the diffusiophoretic process is positive (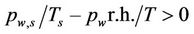), the droplets evaporate, and by including hydrodynamic Stefan flow, the diffusiophoresis pushes the particles away from the droplets [55]. Therefore thermophoresis and diffusiophoresis act in a reverse way, not in the same way, as claimed by the authors, who write that “as r.h. becomes lower, diffusionphoresis is more effective because particles move to raindrop faster due to rapid evaporation of raindrops, and thus the difference of water vapour density becomes larger”.

In order to evaluate the relative importance of phoresis in the scavenging process, it is also useful to consider published papers on wet scrubbers, devices which can remove even particles smaller than a few micrometers from indoor or industrial gases, by bringing them into contact with liquid droplets.

Sparks and Pilat [56], Pilat and Prem [27,28] calculated particle collection efficiencies for a single droplet (d = 100 μm) and for spray droplet scrubbers, considering inertial impaction, diffusiophoresis and thermophoresis, showing that positive diffusiophoresis (condensation) could substantially improve the collection efficiency of sub-micron particles. It was also seen that the effect of phoretic forces becomes greater as the droplet size is increased, because of the longer time necessary to come into equilibrium with the gas. The model assumed a potential flow for the gas flow profile around the droplet moving at settling velocity and a stagnant gas layer surrounding the droplet across which exists a vapour and temperature gradient. However, according Wang et al., [30], at the considered Reynolds number, the viscous nature of flow of air past drops is still of great importance and the temperature gradients considered by the above authors are not typically found in the atmosphere.

Horst [57] considered the scavenging of aerosol from gas for a condensing steam/air system on a cold wall, assuming that the steam/air system was saturated everywhere. Following Waldmann and Schmidt theory, he found that the particles are carried in the direction of water vapour flux at a velocity: V = 10³ m_w (m_w, mass flux of vapour, g·cm^–2·s^–1; V, cm·s^–1), two orders of magnitude higher than thermophoretic velocity.

Viswanathan [58] performed a similar numerical study, for a range of collector radii between 50 and 4000 mm and particle size range between 0.05 and 10 mm, to include particles in the “Greenfield gap”, by considering Stokes flow. The results for a water temperature of 10˚C and a gas temperature ranging between 20˚C and 95˚C show an increase of particle collection efficiency of several orders of magnitude, which is most prominent at lower Reynolds number.

It is worth noting that both Pilat and Prem [27,28], and Viswanathan [58] considered the temperatures of the drop and of the air to be constant (T_air > T_drop), with thermophoresis and diffusiophoresis consequently behaving in the same way. This assumption does not always reflect the atmospheric situation. The relative importance of phoretic phenomena is also highlighted both theoretically and experimentally from Vasudevan et al. [59] in the removal of particulate from fuel gas in spray scrubbers.

3. Laboratory and Fields Studies on Drop Scavenging, In-Cloud and Below-Clouds

3.1. In-Cloud Scavenging

It should be noted that the distinction between in-cloud and below-cloud scavenging is not absolute, as precipitation which forms at higher altitude, falling into a cloud layer, leads to scavenging even within the cloud. Here, the review focuses on only a few published papers, which consider phoretic forces in the in-cloud scavenging process.

The phenomena of thermoand diffusiophoresis were predicted by Stefan [3] and subsequently observed by Facy [60]. Facy was the first to suggest that diffusiophoresis may contribute to the scavenging of the atmospheric aerosol during cloud droplet growth. He photographed growing and evaporating water drops in an aerosol-laden atmosphere and showed that a dust-free space surrounded the evaporating drop, due to diffusiophoretic forces set up by the flux of water vapour away from the drop. Conversely, a growing drop encouraged the migration of aerosol to the surface of the drop.

Goldsmith et al., [46] conducted a cloud-chamber experiment in which salt droplets were grown up to 10 μm in radius in the atmosphere of a radioactive aerosol (0.01 μm - 0.1 μm). They assessed the absolute efficiency of the diffusiophoretic mechanism in capturing the submicron particles by the growing droplets. Concerning the role of diffusiophoresis in the atmosphere, the authors concluded that the efficiency of diffusiophoresis in scavenging particles from the atmosphere should be low, for each condensation cycle inside a cloud, compared with any other processes. However, the overall efficiency is dependent on the number of condensation-evaporationcondensation cycles taking place in natural clouds. It should be pointed out that in the performed experiments thermophoresis and diffusiophoresis were present simultaneously, and the results showed a prevalence of diffusiophoresis with respect to thermophoresis by considering sub-micron particles.

Phoretic forces could play a role in the discrepancy observed in mixed clouds between the concentration of ice nuclei and ice particles. There are abundant observations of enhanced ice formation in regions where cloud droplets are evaporating in cumuliform, stratiform, and wave clouds [49,61-67]. Moreover, it has been speculated that contact nucleation of aerosol on the external surface of the supercooled droplets may be responsible for this “evaporating freezing”. On considering the contribution of phoretic effects, it should be concluded that thermophoresis is prevalent with respect to diffusiophoresis.

Cooper and Vali [68] studied simple layer clouds. The patterns in the development of ice in these clouds suggest that ice originates in association with the initial condensation process, near the upwind edge of the cloud. Since continuous ice production does not occur beyond that region, the ice development can be attributed to condensation-freezing and contact nucleation. In this case a prevalence of diffusiophoresis during water vapour condensation should be present.

These contradictory results was possibly overcome by Durant and Shaw [69], whose laboratory experiments showed that the freezing temperature of an evaporating supercooled drop will suddenly become higher, once an immersed ice nucleus contacts the internal drop surface (“evaporation freezing”). That is to say, when a particle is immersed and very near or touching the surface of a supercooled droplet, it is a better ice nucleus than when it is far from the surface. The difference in the two modes of nucleation was found to be between 4˚C and 5˚C for all the materials tested. Therefore the notion of contact nucleation should be generalized to include surface crystallization from particles contacting a supercooled drop from the inside-out, as well as from the outside-in. In conclusion, if internal contact nucleation were the prevalent freezing mechanism in the above reported cases of evaporating cloud droplets, the hypothesis that thermophoresis was prevalent over diffusiophoresis should decline.

Ladino et al., [70] performed experiments in the CLINCH chamber, using pure water droplets of radii between 12.8 and 20.0 μm, allowed to fall freely, and to collide in laminar flow with particles having radii between 0.05 and 0.33 μm. Evaporation of the droplets was taken into account since the relative humidity inside the chamber was below 100%. Even if the data are very scattered, for droplet size at 12.8 μm and particle radii in the range from 0.05 to 0.33 μm, a decrease of the collection efficiency can be observed, higher than the Wang et al., [30] theoretical model, with a minimum at about 0.25 μm. The trend is partially in agreement with previous experimental studies by Lai et al., [71], performed with much higher drop diameter. In addition, in experiments with a fixed aerosol radius (0.24 μm), Ladino et al., [70] found a decrease of collection efficiency with increasing droplet size (12.8 - 20.0 μm) as predicted by theory [30], although values were smaller by up to one order of magnitude (r.h. = 90%). This could mean that for evaporating droplets diffusiophoresis decreases the scavenging.

3.2. Below-Cloud Scavenging

Considering laboratory experiments, the different experimental conditions (temperature, relative humidity, droplet and aerosol diameter, etc.), make it difficult to compare results. Several laboratory measurements of capture efficiency have been made, disregarding the relative humidity present in the experimental apparatus, making it impossible to evaluate the contribution of thermodiffusiophoresis [71-73].

In some cases the humidity in the experimental apparatus has been measured. In a laboratory experiments, Pranesha and Kamra [74] considered particle size (1.9 μm - 6.4 μm) and 3.6 mm - 4.8 mm diameter drops. The collection efficiency increased as the particle size increased for a fixed drop size, and decreased sharply with increasing drop size for each particle size. Although the humidity in the aerosol chamber was observed to be between 35% to 50%, the authors claim that evaporation from the surface of the drops was expected to be negligible, and consequently phoretic effects were not considered.

Ebert et al., [75] performed a field experiment in which aerosol (radius varying from 0.19 to 1.8 μm) was used to measure particle scavenging processes in the atmosphere during real precipitation events. Even if the r.h. varied between 65% - 100% during the experiments, no evaluation was made concerning the effect of phoresis.

The first laboratory experiment considering all the scavenging mechanisms (Brownian diffusion, hydrodynamic, phoretic and electrical effects) was performed by Wang and Pruppacher [76]. Water drops (150 to 2500 mm equivalent radius) were allowed to fall through an aerosol chamber in sub-saturated air. Although their data show good agreement with the efficiency calculations of Grover et al., [29] as far as the dependence on the drop size was concerned, their measurements were for only one particle size (0.25 μm radius; 23% r.h.). The collection efficiency showed a minimum for 200 μm drop radius and decreased for drop with radius higher than 500 mm.

The authors write: “despite the agreement found between theory and experiment, it appears necessary to test the theory of Grover for other temperature and humidity conditions and for additional drop and particle sizes”.

Leong et al., [77] investigated the effect of particle size (0.58 μm - 3.2 μm radius) on scavenging for evaporating cloud drops at 30% r.h., with mean radii of 55 to 93 μm. Good agreement between experiments and theory was found for larger particles scavenged by inertial impaction, but not for the smaller ones also scavenged by phoretic forces [29].

In an effort to evaluate the contribution of phoretic forces in the scavenging process, Wang et al., [78] performed experiments assuming a quasi steady-process and comparing the collection efficiency obtained with a water droplet evaporating (500 μm radius) and an oil droplet with very low vapour pressure, in the same experimental conditions. The data obtained indicated that for 500 μm diameter droplets an efficiency of 1.6 × 10^–3 can be attributed to phoretic forces.

Concerning field measurements, the scavenging coefficient is usually calculated from measurements of change in aerosol size distribution with different rainfall in different environments. For very small and very large particles, there is prevalently an agreement with theoretical studies [19,25,38]. However, theoretical parameterizations prevalently underestimate observed L values by one to two orders of magnitude for particles in the 0.1 μm - 1 μm radius range and by one order of magnitude for particles smaller than 0.1 mm, compared to the available field measurements [79].

To avoid experimental biases, it should be guaranteed that in the course of precipitation the air at the measuring station is not replaced by another mass with a different aerosol loading, i.e. no significant convective activity should be present and no frontal passage should occur over the time of interest. This requirement is not always met in field experiments. In addition, a change of r.h. during the event may alter the aerosol size distribution due to hygroscopic effects. Since L is very sensitive function of the aerosol diameter, a change of r.h. will result in a change of the depletion rate. Precipitation is hardly even a constant process. Large fluctuations in the rainfall rate and the drop size distribution are often observed. These parameters influence L directly. If the above requirements are fulfilled, the differences between theoretical and experimental data could depend on theoretical reasons, i.e. on the fact that phoretic forces acting upon submicron particles are underestimated by theory, on vertical turbulent diffusion, or on the dependence of the scavenging coefficient on aerosol chemical composition [80-82].

Davenport and Peters [51] analysed wash-out coefficients for moderate rains (1.1 mm·h^–1 to 3.0 mm·h^–1) over sampling times of 5 to 6.5 hours. Based on data collected during the events, the authors claimed that theoretical scavenging coefficients agree quite well with experimental results in the coarse aerosol range. For particle in the range 0.007 μm - 0.022 μm and 0.4 μm - 1 μm, the model which consider inertial impaction, interception, Brownian diffusion, and phoresis, predicted one or two orders of magnitude less than field measurements. No available experimental data concerned aerosol in the 0.02 μm - 0.4 μm range. The results of Davenport and Peters are rather surprising, as they did not find any dependence on aerosol radius at all in their scavenging coefficients in the measured ranges. One may speculate that scavenging effects were not properly distinguished from transport phenomena.

Moreover, Radke et al., [83] measured the scavenging of aerosol particle (natural “man made” as well as plume and volcanic aerosol, d > 0.01 μm) mainly by showertype precipitation. Despite large variations in the nature of the aerosol particles and precipitations, the scavenging collection efficiencies as a function of particle size showed marked similarity. For particles ³ 1 μm in diameter, where inertial impaction dominates scavenging, measurements were in good agreement with the theoretical results of Dana and Hales [84], Wang et al., [30] and the laboratory measurements of Lai et al., [71]. For submicron particles the scavenging collection efficiencies were generally much higher than values theoretically predicted for scavenging due to Brownian and phoretic effects.

Schumann [85], Volken and Schumann [86] performed a field study on Mt-Rigi (central Switzerland), measuring the below-cloud scavenging of aerosol particle during 7-year winter precipitations. The scavenging coefficient showed a dependence on particle diameter.

For particle smaller than about 0.6 μm, the value of L was 10^–5 s^–1 on average, increasing to values around 3 × 10^–5 s^–1 for particles 1 μm < d < 3 μm. A small local maximum near 1 μm was also visible. The unexpected result was the absence of an evident minimum of the scavenging coefficient. Based on data collected during the events (raindrop size distribution, relative humidity), and collection kernels from Flossmann [87], the theoretical scavenging coefficients calculated agreed quite well with experimental results in the coarse aerosol range, while for submicron particles they tended to be 20 - 40 times smaller. An attempt was made to explain the differences, by considering the influence of r.h., the particle shape, electric effects, and phoretic forces.

Laakso et al., [53] studied the dependence of the scavenging coefficient for particle diameters of 10 - 500 nm and for rain intensity 0 - 20 mm·h^–1 at a boreal forest site in Southern Finland. When the rain intensity increased from 0.5 to 9 mm·h^–1, the corresponding scavenging coefficient changed from 1 × 10^–5 to 4 × 10^–5 s^–1. The scavenging coefficient showed a very little size dependence, with a minimum in the 0.1 μm - 1 μm range. In the accumulation size range, the results were higher than those suggested by theories presented by Slinn [14], Schumann [85] and McGann and Jennings [48]. To explain the differences, the authors refer to reasons suggested by Volken and Schumann [86].

Chate and Pranesha [88] noted that the collection of atmospheric particles during thunderstorm rain by the mechanisms of Brownian diffusion, directional interception, inertial impaction and electrostatic charge effects cannot adequately explain the depletion in particle number concentrations observed during these field experiments. They suggested that the phenomenon of thermophoresis, diffusiophoresis, coagulation and condensational growth of hygroscopic particles may be important during thunderstorm rain as removal processes for atmospheric particulate.

In conclusion, it seems that even parameterizations which take into account the additional collection processes due to thermophoresis, diffusiophoresis, and electrostatic forces, are not able to explain the discrepancies between field and observed scavenging coefficient in the “Greenfield zone”.

4. Conclusions

The review of the published papers on the role of phoretic forces in atmospheric scavenging of aerosol can be summarized as follows:

• Theoretical models agree that Brownian diffusion appears to dominate scavenging of aerosol in the size r < 0.1 μm range, while inertial impaction dominates scavenging in the size r > 1 μm range. Thus, there is a minimum collection efficiency for particles in the approximate range of 0.1 μm - 1 μm, where phoretic and electric effects are felt. The exact depth, width and position of this minimum depend on the properties of the aerosols and hydrometeors, and on ambient conditions.

• By considering in-cloud scavenging, where scavenging theories assume a thermal equilibrium between the drop and the environment, evaporation being considered the only factor determining the temperature gradient, thermophoretic and diffusiophoretic forces (by including Stefan flow) act in the opposed direction. Considering as an example an evaporating droplet, the thermophoretic force should push the aerosol towards the droplet, and diffusiophoresis should push the aerosol away from the droplet. Disagreement exists in both laboratory experiments and the theoretical model on the prevalent force. Some authors evaluate thermophoresis as prevalent for particles of radius less than 1 μm, while diffusiophoresis is prevalent for particles with higher radius.

• Considering below-cloud scavenging, the proposed theoretical models follow different approaches. Chate [52], Andronache et al., [32], and Bae et al., [33] assume a constant temperature for droplets and air, neglecting the variation of droplet temperature due to growth or evaporation. In our opinion, the above authors in the theoretical approach consider only thermophoresis and pure diffusiophoresis, by neglecting Stefan flow. Considering an evaporating droplet, the movement of the aerosol due to diffusiophoresis process was considered towards the droplet, while by including the Stefan flow the aerosol should be rejected.

• Studies on the scavenging process in spray water scrubbers, based on the mechanisms valid in the atmosphere, highlight a prevalence of diffusiophoresis with respect to thermophoresis.

• Concerning field measurements, for very small and very large particles, there is generally an agreement with theoretical studies. However, significant discrepancies between observations and theoretical estimates have been found for sub-micron particles in the “Greenfield gap”, with measured values being one to two orders of magnitude higher than predicted. This discrepancies remain even the contribution of phoretic forces is considered.

• In conclusion, more laboratory experiments under controlled conditions and the collection of field data under different rain conditions and other environmental conditions are required, to evaluate the contribution of phoretic forces to the scavenging processes.

REFERENCES