Soft Nanoscience Letters
Vol. 2 No. 4 (2012) , Article ID: 23421 , 6 pages DOI:10.4236/snl.2012.24013
The Modeling and Study of Depletion Interaction at Mixture of C12E5 Microemulsion with Polyethylene Glycol Polymer
![]()
1Department of Physics, University of Sistan and Baluchestan, Zahedan, Iran; 2Institut für Experimentelle Physik, Universität Ulm, Ulm, Germany.
Email: *soheil.sharifi@gmail.com, *masoud.amirkhani@uni-ulm.de
Received May 28th, 2012; revised June 30th, 2012; accepted July 28th, 2012
Keywords: Nano-Droplet; SAXS; Light Scattering; Polyethyl Glycol
ABSTRACT
he photon correlation spectroscopy and small-angle X-ray scattering is used for study the mixture of C12E5 microemulsion with PEG in order to determine structure and dynamic of the system. Photon correlation spectroscopy experiment showed an exponential relaxation for pure C12E5 microemulsion that come from Brownian motion of oil nano-droplets in water. The shape of the relaxation changed with increasing of PEG concentration in the C12E5 microemulsion, (relaxation becomes non-exponential with the increase of PEG), which demonstrates an increase of cooperatively in the C12E5 microemulsion. The SAXS experiment was used to study the structure of the system, and a model consists of a mixture of core-shell spheres with an Asakura-Oosawa interaction was applied to analyze data.
1. Introduction
The polymer-induced depletion interaction between microemulsion droplets is the interesting topic in soft matter physics. Understanding depletion phenomena is relevant for many reasons, and it plays an important role in many industrial and biological applications. For example, the depletion interaction leads to phase separation of colloidal dispersions [1], protein crystallization [2], red blood cells clustering [3], and the helical conformation of long molecular chains [4]. In the mixture of non-adsorbing polymer with microemulsion [5-8], near the surfaces of droplets, there exists a depletion volume usually characterized by a depletion layer thickness. In the depletion regions, the polymer density varies from zero to the value of the bulk phase, due to the restrictions of conformational entropy of polymers. When two droplets of microemulsions approach each other, (the depletion regions overlap), an osmotic pressure producing between the outside and inside region of objects. This osmotic pressure difference pushes the two objects (for example, droplets) together and induces the so-called depletion effect. This effect embodies the change of conformational entropy of the droplets. In the mixture of colloidal systems with polymers, for entropic reasons the polymers chains avoid the space between two close particles and create an effective attraction among the colloid particles. This depletion interaction has been used to explain phase diagrams of colloid-polymer mixtures, [9] and is believed to be important for a variety of interesting colloid systems such as casein micelles, [10] hemoglubine, [11] and globular proteins, [12].
Ternary microemulsions, consisting of water, decane, and nonionic surfactant, pentaethylene glycol dodecyl ether (C12E5), have been well characterized by many researchers, [13-15]. These systems can form different structure such as an oil-in-water droplet microemulsion, a lamellar structure, a bi-continuous microemulsion, or a hexagonal structure depending on the concentration and temperature. The thermodynamic properties of the C12E5 microemulsion at a constant surfactant-to-oil weight ratio of 1.08 had been studied extensively, and the system is well understood. The C12E5 microemulsion at this weight ratio, shown a L1 phase of globular droplets between 24˚C to 30˚C and phase diagram of microemulsion is changing with added polymer to the microemulsion. The C12E5 microemulsion showed a single relaxation and well-defined spherical oil droplets with hydrocarbon radius 75 Å and low polydispersity [16]. The viscosity and light scattering of the mixture of PEG with C12E5 microemulsion was studied and analyzed within polymer depletion theory, [17-19]. In that studied, SAXS and dynamic light scattering (DLS) were used to confirm that C12E5 microemulsions behave as hard-sphere dispersions. In present work we used the different molecular weight of the polyethylene glycol and focused on the structural and dynamical behavior of C12E5 microemulsion. We studied the effect of increasing concentrations of a nonadsorbing polymer, polyethylene glycol (PEG), on the structure and relaxation of droplet of nanionic microemulsions (C12E5 microemulsions) with small-angle X-ray scattering (SAXS) and dynamic light scattering.
2. Experimental
2.1. Materials and Methods
The Pentaethylene glycol monododecyl ether (C12E5), n-decane and polyethylene glycol (PEG) (Mn = 2200) were obtained from Sigma-Aldrich. Chemicals were used as received and MilliQ water was used in preparing all samples. The bottles of C12E5, which are hermetically sealed, have always been stored in a refrigerator well below the melting point (23˚C). After a container was opened, the surfactant was stored in a nitrogen environment; it was still found that the surfactant did not remain stable for more than a month. The samples were prepared by mixing the components directly in glass a ampoule in order to minimize the number of transfers and the glass ampoules were tightly sealed with a gas flame. The microemulsions were prepared by weight, in terms of surfactant-oil mass ratio of 1.08 and the mass fraction of droplets (mf, drop = (mDec + mC12E5)/(mTotal)), which varies by the respective mass of n-decane (mDec), C12E5 (mC12E5) and total sample mass (mTota). The mi-croemulsions are thermodynamically stable dispersions in oil-in-water (O/W) droplets surrounded by a surfactant film: For these O/W microemulsions, it has been shown that the microemulsion phase (L1) is wellmodeled as a dispersion of hard-sphere particles. In all experiments, the mass ratio of surfactant to the oil is constant and with a hydrocarbon core radius of 75 Å over a wide range of droplet concentrations, when the system is near the limit of maximum oil solubilization. The samples of microemulsions with polymer were prepared by weight in the terms of the mass fraction of triblock polymer (mf, poly = mpoly/(mTotal)) that mpoly is the mass of polymer in the sample. The mixed samples were prepared at a constant mass fraction of droplets (mf,drop = 0.1) and a surfacetant-oil mass ratio of 1.08 with the different mass fractions of polymer. The samples were thoroughly shaken to ensure homogenization and then kept at the temperature 26˚C in a water bath for several days before the experiment. We observed that all samples were transparent at 26˚C.
2.2. Small-Angle X-Ray Scattering
Small-angle X-ray scattering (SAXS) measurements were performed using the pinhole SAXS instrument at the Aarhus University, [20]. The instrument consists of an X-ray camera (NanoSTAR, Bruker AXS) with a rotating anode X-ray (Cu Ka radiation) source, cross-coupled Göbel mirrors, collimation using three pinholes, an evacuated beam path, and a 2D position-sensitive gas detector (HiSTAR). The experiments were done at a fixed wavelength of = 1.54 Å and two different sample-detector distances. In the current experiments small pinholes were used, giving a range of scattering vectors as 0.004 < q(1/Å) < 0.2, where q is the length of the wave vector, q = 4sinθ/λ. In this expression is half the scattering angle. Samples were held in 1.7 mm quartz capillaries and measurements were made at 20˚C the scattering from capillaries filled with water was measured as background and was subtracted to yield the scattering as a function of q for the microemulsion samples with PEG.
2.3. Dynamic Light Scattering
The equations are an exception to the prescribed DLS measurements were performed using an ALV singledetector version compact goniometer system, from ALVGmbH, Langen, Germany. The light source is a He-Ne laser, operating at a wavelength of 632.8 nm with vertically polarized light. The beam was focused on the sample cell through a temperature-controlled cylindrical quartz container (with two plane-parallel windows), which is filled with a refractive index matching liquid (toluene). All the correlation functions in this work were fitted by a single stretched exponential function.
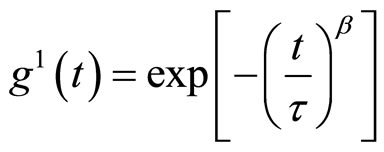 (1)
(1)
The stretched exponential function describes the decay processes that have a distribution of relaxation times . The parameter
. The parameter 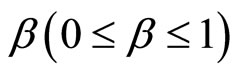 measures the width of the distribution function. A smaller β value corresponds to a broader distribution of relaxation times or more cooperative movement [14-16]. The mean value of the relaxation time is given by
measures the width of the distribution function. A smaller β value corresponds to a broader distribution of relaxation times or more cooperative movement [14-16]. The mean value of the relaxation time is given by
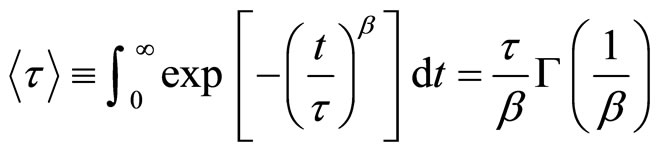 (2)
(2)
where Γ is the gamma function and the collective diffusion constant [21] was calculated through Dc = 1/q2 < τ >.
3. Results
3.1. Dynamic Light Scattering
Figure 1 shows time correlation function data (at a scattering angle of 90˚) for a polymer mass fraction of 0.027. The decay of the time correlation function shows a single relaxation that can be well described by Equation (1) for

Figure 1. The first-order field correlation function versus time for C12E5 microemulsion at a droplet mass fraction of 0.098 and polymer mass fraction of 0.027 at the temperature 26˚C.
all the samples at 26˚C. The fittings of the correlation functions for the pure microemulsion show that the size distribution of the particles is not changing when changing the droplet mass fraction and that it is rather narrow (β = 0.98), Figure 2. The value of β for mixed polymer and microemulsion is slightly lower than for pure microemulsion, which demonstrates that either the polydispersity or cooperativity [20] of the mixed system is increased by the addition of the polymer (Figure 2). In addition Figure 2 illustrates that is decreasing by increasing the mass fraction of droplet and for the lowest droplet mass fraction, the value is virtually not affected the addition of polymer. The size of the droplets in the microemulsion in the presence of non-adsorbing polymer is expected to be constant [17,22], so the decreasing value of β can be attributed to cooperative movement due to the depletion effect. At the lower droplet mass fraction with the increase of the polymer amount, β decrease less significantly compares to the higher droplet mass fraction. So, decreasing β values at lower droplet mass fraction can be rationalized by decreasing depletion effect. From Figure 3, one sees that the diffusion constant decreases monotonously with increasing PEG concentration for all systems, and is lower for the higher mass fraction of the polymer. Moreover the general trend depicted in Figure 3 is that adding increased amount of PEG results in the slop of collective diffusion versus droplet mass fraction and the intercept (the dilute-limiting value of diffusion constant) decrease. This trend is attributed to the change of interaction between microemulsions from repulsive to the attractive interaction [23]. This is a typical behavior that has been reported previously for the mixture of the C12E5 microemulsion and PEG, [17].
3.2. SAXS Experiment
The structure of the C12E5 microemulsions at the different

Figure 2. The β value of the mixtures of C12E5 microemulsion for different polymer mass fractions (mf, poly = 0¢, 0.015▲, 0.022˜, 0.027▼), versus the mass fraction of droplets at temperature 26˚C.

Figure 3. The diffusion coefficient of the mixtures of C12E5 microemulsion with different polymer mass fractions (mf, poly =0¢, 0.015˜, 0.022▲, 0.027▼), versus the mass fraction of droplets at temperature 26˚C.
concentrations of droplets (oil and surfactant) has previously been studied by SAXS and small-angleneutron scattering in the L1 phase of the microemulsion, [14-16]. In the present work, the variation of structure of the C12E5 microemulsion under addition of the PEG is investigated by SAXS.
For analyzing the data, we applied a model for a mixture of core-shell spheres with an added depletion attracttion due to dissolved non-adsorbing polymer. The scattering intensity as function of the scattering vector I(q) of spherical, monodisperse particles can be describe with a form factor componentt F(q), which is proportional to the scattering of a single particle, and a structure factor S(q), which describes the interaction effect:
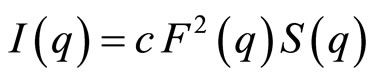 (3)
(3)
c being a prefactor, which contains the number density of scattering particles. For the general case of n shells around a spherical droplet core the form factor reads.
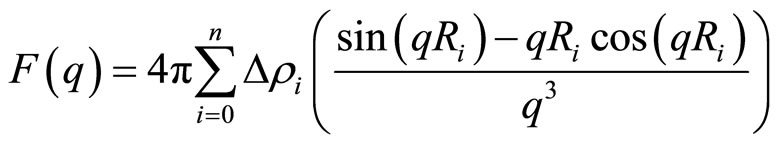 (4)
(4)
where Ri is the radius of the ith shell or, respectively, the core R0 and ∆ρi is the electron density contrast between the shells i and i + 1 with ρn + 1 and ρ0 being the electron density of the solvent and the core, respectively. So, for a simple core-shell micelle n = 1. The structure factor is the Fourier transform of the pair correlation function g(r).
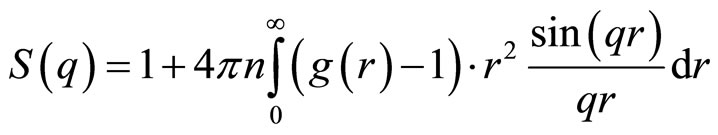 (5)
(5)
The pair correlation function gives the probability to find another particle at a distance r from the center of a given particle, relative to the probability to find a particle at this distance in an ideal gas. It is closely related to the total correlation function h(r) = g(r) − 1 and it can by means of the Ornstein-Zernike equation [27,28]. Be linked to the direct correlation function c(r), which comprises all the correlation effects due to direct interactions between the particles
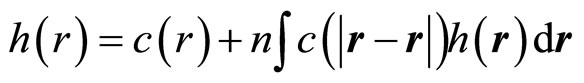 (6)
(6)
The depletion effect is modeled by the so-called Asakura-Oosawa (AO) theory which assumes pair-wise additive attraction [24]. The depletion attraction is caused by the change in osmotic pressure of a non-adsorbing polymer or by the presence of other colloidal particles. It can be approximated in the range 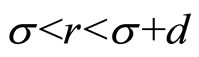 by following equation, [25]:
by following equation, [25]:
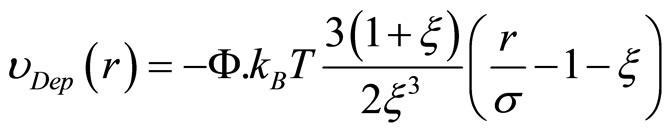 (7)
(7)
Where σ is the diameter of the large particles and d the diameter of the small particles or the radius of gyration of the polymers, ξ = d/σ is a size ratio, where σ is the diameter of the large particles and d the diameter of the small particles or the radius of gyration of the polymers. Ф is the volume fraction of the small particles, and r is the centre to centre distance of the colloids, while kBT is the Boltzmann constant times the absolute temperature. The volume fraction Ф is the volume of the small particles relative to the free volume, i.e. the total volume subtracted from the volume of the large particles and their depletion zones, which can be calculated from the volume fraction of the large particles and the size ratio, [26].
The program was available that numerically solves the so-called Ornstein-Zernike equation for the partial structure factors using the so-called Percus-Yevick closure and the AO depletion interaction. Good fits were obtained for the region of low q to slightly beyond the main structure factor peak but the fits were poorer at high q, where the form factor dominates. To solve the problem in the high-q, we removed the high-q points in the Asakura-Oosawa model and replace them with the form factor with an infinitely dilute core-shell system.
4. Discussion
From the SAXS measurement we obtained detailed information about the variation of structure with depletion effect. The change in the interaction between the micelles at the small amount of PEG is observed in the structure factor, Figure 4. With increasing concentration of PEG the structure factor at the low q (q ≈ 0), increase that show increase of repulsive interaction between droplets. The structure factor at the low q was studied with SAXS experiment for polymers, [29], proteins, [30] and particles, [31] that results show the structure factor at the low q is increased with the increase of the repulsive interacttion between droplets that is in agreement with our results. The results of light scattering also show the pure microemulsion have attractive interaction but with the increase of PEG concentration interaction of droplet change to the repulsive, figure 3. The formation of a distinct first-order maximum followed by a second-order maximum in the structure factor clearly shows the order in the system doesn’t change with the increase of polymer concentration. The GIFT analysis showed, with the increase of polymer mass fraction of 0.015 to 0.027, the size ratio (ξ) in the mixture of PEG with C12E5 microemulsiom change from 0.5 to 0.3 that describe increase of polymers size in the solution, Table 1.
From the dynamic light scattering, we observed a single relaxation process for the pure microemulsion and mixed microemulsion with PEG but the shape of relaxation (β) change with the increase of the PEG concentration. The amount of PEG in microemulsion changes the interaction between droplets that is in agreement with SAXS results, Figure 5. The collective diffusion coefficient of the C12E5 microemulsions decreases with the increasing droplet mass fraction that indicates an attracttive interaction in the C12E5 microemulsions. Our study of the collective diffusion coefficient shows the interacttion between droplets changes from attractive to repulsive in the C12E5 microemulsions, with the increase of PEG concentration. In mixtures of PEG with C12E5 microemulsion, PEG did not induced any order structure in the microemulsion, due to the non-adsorbing nature of interaction between PEG and C12E5 microemulsion. However, PEG can increase the attractive interaction between the droplets, as one sees from light scattering experiments, Figure 3. The best model for the describing the effect of PEG on the C12E5 microemulsion is terms of an attractive sphere model with depletion potential. Our results with analysis data with model showed that polydispersity

Table 1. The values used for modeling the SAXS data as a mixture of core-shell spheres with an added depletion attraction due to dissolved non-adsorbing polymer, where ξ = d/σ where σ is the diameter of the droplet and d the diameter of the polymer. Mc (mean core radius), Mc + s (mean core + shell radius), dmf (droplet mass fraction), pmf (polymer mass fraction).

Figure 4. The SAXS experiment of the mixture of C12E5 microemulsion at constant droplet mass fraction (0.098) and mDec/mC12E5 = 1.08 with different concentration of PEG (mf, pol = 0.015¡, 0.022▲, 0.027▼) and the lines are the fit with core - shell spheres with an added depletion attraction at low q (q < 0.048 1/Å) and the model with infinitely dilute core-shell system at high q.
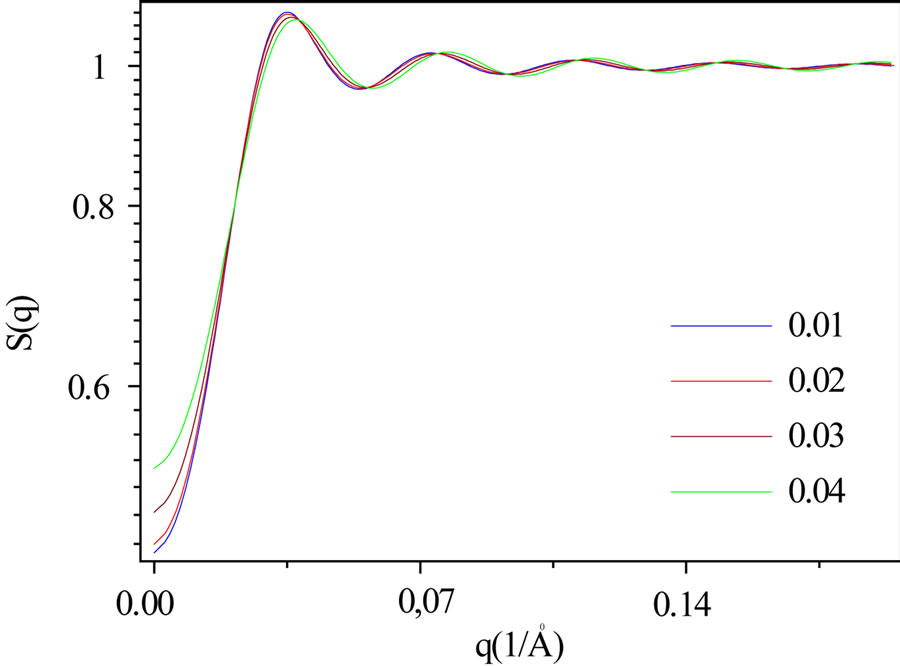
Figure 5. Structure factor as a function of q for different mass fraction of PEG (M.n = 2200) (mf, pol = 0.01, 0.02, 0.03, 0.04) mixed with C12E5 microemulsions at constant mass fraction of droplet (0.1) and mDec/mC12E5 = 51.9/48.1 at 23˚C .
and size of droplets are constant with the increase of the PEG concentration, Table 1.
5. Conclusion
Small-angle X-ray scattering and dynamic light scattering were used to study the mixture of C12E5 with PEG. Our results show the stretched exponential exponent, β, decrease, from 0.98 to 0.92 with the increase of the mass fraction of the droplet for all PEG concentration in the C12E5microemulsion, which demonstrates increase of the cooperativity between droplets. Morever, the study of theC12E5microemulsion at differentt droplet mass fraction shows transition from repulsive to attractive interaction by increasing the PEG content. We used an attractive monodisperse sphere model and polydisperse hard sphere model with size polydispersity governed by a Schulz distribution to analyzing the SAXS data of mixture of PEG with C12E5 microemulsion.
6. Acknowledgements
This work was supported by the University of Sistan and Baluchestan and SFB-569 (DFG) the Research Collaborative Center of the Institut für Experimentelle Physik, Universität Ulm.
REFERENCES
- D. H. Napper, “Polymeric Stabilization of Colloidal Dispersions,” Academic Press, New York, 1983.
- R. Tuinier, J. Rieger and C. G. de Kruif, “Depletion-Induced Phase Separation in Colloid-Polymer Mixtures,” Advanced Colloid Interface Science, Vol. 103, No. 1, 2003, pp. 1-31. doi:10.1016/S0001-8686(02)00081-7
- S. Sharifi and M. Amirkhani, “Light Scattering Study of Mixture of Polyethylene Glycol with C12E5 Microemulsion,” Soft Nanoscience Letters, Vol. 1, No. 3, 2011. doi:10.4236/snl.2011.13014
- V. Snir and R. D. Kamien, “Entropically Driven Helix Formation,” Science, Vol. 307, No. 5712, 2005, p. 1067. doi:10.1126/science.1106243
- X. Ye, T. Narayanan, P. Tong, J. S. Huang, M. Y. Lin, B. L. Carvalho and L. J. Fetters, “Depletion Interactions in Colloid-Polymer Mixtures,” Physical Review E, 54, 6, 1996, p. 6500. doi:10.1103/PhysRevE.54.6500
- S. Sharifi and A. Alavi, “Dynamic Light Scattering Study of Microemulsion,” Proceedings of SPIE, Vol. 8001, 2011, pp. 80012R-80012R-8. doi:10.1117/12.892990
- I. Lynch, S. Cornen and L. Piculell, “Investigation of the Segregative Phase Separation Induced by Addition of Polystyrene to AOT Oil-Continuous Microemulsions,” The Journal of Physical Chemistry B, 108, 17, 2004, p. 5443. doi:10.1021/jp0493834
- S. Yang and D. D. Yan, H. G. Tan and A.-C. Shi, “Depletion Interaction between Two Colloidal Particles in a Nonadsorbing Polymer Solution,” Physical Review E, Vol. 74, No. 4, 2006, p. 041808. doi:10.1103/PhysRevE.74.041808
- H. N. W. Lekkerkerker, “Interactions, Phase Transitions and Metastable States in Concentrated Colloidal Dispersions,” Physica A, Vol. 213, No. 1-2, 1995, p. 18. doi:10.1016/0378-4371(94)00144-I
- R. Tuinier, E. ten Grotenhuis, C. Holt, P. A. Timmins and C. G. de Kruif, “Depletion Interaction of Casein Micelles and an Exocellular Polysaccharide,” Physical Review E, Vol. 60, No. 1, 1999, p. 848. doi:10.1103/PhysRevE.60.848
- J. Janzen and D. E. Brooks, “Do Plasma-Proteins Adsorb To Red-Cells,” Clinical Hemorheology and Microcirculation, Vol. 9, 1989, p. 695.
- A. M. Kulkarni, A. P. Chattarjee, K. S. Schweizer and C. F. Zukoski, “Depletion Interactions in the Protein Limit: Effects of Polymer Density Fluctuations,“ Physical Review Letters, Vol. 85, No. 22, 1999, p. 4554. doi:10.1103/PhysRevLett.83.4554
- S. Sharifi, M. Amirkhani, J. M. Asla, M. R. Mohammadi and O. Marti, “Light Scattering and SAXS Study of AOT Microemulsion at Low Size Droplet,” Soft Nanoscience Letters, Vol. 2, No.1, 2012, pp. 8-12. doi:10.4236/snl.2012.21002
- M. Nayeri, M. Zackrisson and J. Bergenholtz, “Scattering Functions of Core—Shell-Struct Ured Hard Spheres with Schulz-Distributed Radii,” The Journal of Physical Chemistry B, Vol. 113, 2009, p. 8296. doi:10.1021/jp811482w
- M. Schwab and B. Stühn, “Relaxation Phenomena and Development of Structure in a Physically Cross Linked Nonionic Microemulsion Studied by Photon Correlation Spectroscopy and Small Angle X-Ray Scattering,” Journal of Chemical Physical, Vol. 112, No. 14, 2000. pp. 6461-6471. doi:10.1063/1.481207
- M. Amirkhani, S. Sharifi and O. Marti, “The Effect of Simultaneous Size Reduction and Transient Network Formation on the Dynamics of Microemulsions,” Journal of Physics D: Applied Physics, Vol. 45, No. 36, 2012, Article ID: 365302. doi:10.1088/0022-3727/45/36/365302
- M. Zackrisson, R. Andersson and J. Bergenholtz, “Depletion Interactions in Model Microemulsions,” Langmuir, Vol. 20, No. 8, 2004, pp. 3080-3089. doi:10.1021/la036132y
- M. Amirkhani, S. Volden, K. Zhu, W. R. Glomm and B. Nystrm, “Adsorption of Cellulose Derivatives on Flat Gold Surfaces and on Spherical Gold Particles,” Journal of Colloid and Interface Science, Vol. 328, No. 1, 2008, pp. 20-28. doi:10.1021/la036132y
- M. Amirkhani, G. Gorinia and D. Leporinia, “Second Harmonic Generation Studies of Intrinsic and Extrinsic Relaxation Dynamics in Poly (Methy1 Methacrylate),” Journal of Non-Crystalline Solids, Vol. 355, No. 34-36, 2009, pp. 1707-1712. doi:10.1021/la036132y
- S. Sharifi, P. Kudla, C. L. P. Oliveira, J. S. Pedersen and J. Bergenholtz “Variations in Structure Explain the Viscometric Behavior of AOT Microemulsions at Low Water/AOT Molar Ratio,” Zeitschrift für Physikalische Chemie, Vol. 226, No. 3, 2012, pp. 201-218. doi:10.1524/zpch.2012.0173
- J. Appell, G. Porte and E. Buhler, “Self-Diffusion and Collective Diffusion of Charged Colloids Studied by Dynamic Light Scattering,” Journal of Physical Chemistry B, Vol. 109, No. 27, 2005, p. 13186. doi:10.1021/jp051016k
- I. Lynch and L. Piculell, “Size, Concentration, and Solvency Effects on the Viscosifying Behavior of PEO-PSPEO Triblock Copolymers in AOT Oil-Continuous Microemulsions,” Journal of Physical Chemistry B, Vol. 108, No. 22, 2004, pp. 7515-7522. doi:10.1021/jp049147t
- A. Shukla, H. Graener and R. H. H. Neubert, “Observation of Two Diffusive Relaxation Modes in Microemulsions by Dynamic Light Scattering,” Langmuir, Vol. 20, No. 20, 2004, pp. 8526-8530. doi:10.1021/la048883l
- L. S. Ornstein and F. Zernike, “Verh.-K. Ned. Akad. Wet., Afd. Natuurkd.,” Eerste Reeks, Vol. 17, 1914, p. 793.
- S. Asakura and F. Oosawa, “Interaction between Two Bodies Immersed in a Solution of Macromolecules,” Journal of Chemical Physics, Vol. 22, No. 7, 1954, p. 1255. doi:10.1063/1.1740347
- D. I. Svergun and J. S. Pedersen, “Propagating Errors in Small-Angle Scattering Data Treatment,” Journal of Applied Crystallography, Vol. 27, 1994, pp. 241-248. doi:10.1107/S0021889893008337
- J. Bergenholtz, W. C. K. Poon and M. Fuchs, “Gelation in Model Colloid-Polymer Mixtures,” Langmuir, Vol. 19, No. 10, 2003, pp. 4493-4503. doi:10.1021/la0340089
- H. N. W. Lekkerkerker, W. C. K. Poon, P. N. Pusey, A. Stroobants and P. B. Warren, “Phase Behaviour of Colloid + Polymer Mixtures,” Europhysics Letters, Vol. 20, No. 6, 1992 pp. 559-564. doi:10.1209/0295-5075/20/6/015
- S. Finet and A. Tardieu, “α-Crystallin Interaction Forces Studied by Small Angle X-Ray Scattering and Numerical Simulations,” Journal of Crystal Growth, Vol. 232, No. 1-4, 2001, pp. 40-49. doi:10.1016/S0022-0248(01)01160-5
- F. Bonnet, D. Vivar, Ch. Robert and N. Colloc’h, “Interactions in Solution and Crystallization of Aspergillus flavus Urate Oxidase,” Journal of Crystal Growth, Vol. 232, No. 1-4, 2001, pp. 330-339. doi:10.1016/S0022-0248(01)01054-5
- B. Weyerich, J. Brunner-Popela and O. Glatter, “SmallAngle Scattering of Interacting Particles. II. Generalized Indirect Fourier Transformation under Consideration of the Effective Structure Factor for Polydisperse Systems,” Journal of Applied Crystallography, Vol. 32, 1999, pp. 197-209. doi:10.1107/S0021889898011790
NOTES
*Corresponding authors.

