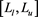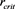International Journal of Astronomy and Astrophysics
Vol.07 No.04(2017), Article ID:80880,18 pages
10.4236/ijaa.2017.74022
Standard and Truncated Luminosity Functions for Stars in the Gaia Era
Lorenzo Zaninetti
Physics Department, via P. Giuria 1, Turin, Italy

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 4, 2017; Accepted: December 3, 2017; Published: December 6, 2017
ABSTRACT
The luminosity function (LF) for stars is here fitted by a Schechter function and by a Gamma probability density function. The dependence of the number of stars on the distance, both in the low and high luminosity regions, requires the inclusion of a lower and upper boundary in the Schechter and Gamma LFs. Three astrophysical applications for stars are provided: deduction of the parameters at low distances, behavior of the average absolute magnitude with distance, and the location of the photometric maximum as a function of the selected flux. The use of the truncated LFs allows modeling the Malmquist bias.
Keywords:
Fundamental Parameters Stars, Luminosity Function, Mass Function

1. Introduction
The stellar luminosity function (LF) is the relative numbers of stars of different luminosities in a standard volume of space, usually a cubic parsec. The determination of the LF for stars is complicated at a local level by the presence of five classes for the stars, as given by the MK system, and by the mass-luminosity relation. The presence of the Malmquist bias, after [1] [2] [3] , for an introduction, see Section 3.6 in [4] or the historical Section 2 in [5] , modifies the distribution in absolute magnitude as a function of the distance and therefore complicates the modeling of the LF for stars.
The LFs for stars started to be fitted by a Gaussian probability density function (PDF) in absolute magnitude, see [6] . In order to deal with the boundaries, a double truncated Gaussian in absolute magnitude has been considered, see [7] . The astronomical derivation of the LF takes account of a standard volume with a radius of »20 pc. As an example [8] has derived the first local LF for stars in a spherical volume having radius of 22 pc and more recently [9] has measured the volume luminosity density and surface luminosity density generated by the Galactic disc, using accurate data on the local luminosity function and the vertical structure of the disc. A new sample of stars, representative of the solar neighborhood LF, has been constructed from the Hipparcos (HIP) catalogue and the Fifth Catalogue of nearby Stars, see [10] .
From the previous analysis, the following questions can be raised.
・ Is it possible to model the LF for stars with the Schechter function and the Gamma LF?
・ Is it possible to model the absolute magnitude-distance plane with the truncated Schechter function or the truncated Gamma LF?
・ Is it possible to model the observational maximum in the number of stars and the average number of stars versus distance at a given flux?
2. The Gaia Catalog
A great number of stars with mean apparent magnitude in the G-band, flux, f, expressed in electron-charge per second (e-/s) and parallax, »two million, are available at the Gaia Data Release 1 (Gaia DR1) astrometric catalogs, see [11] [12] , with data at http://vizier.u-strasbg.fr/viz-bin/VizieR and specific Table I/337/tgasptyc. The above catalog gives stellar parallax, G-band flux, G-band magnitude, Tycho-2 or HIP BT magnitude and Tycho-2 or HIP VT magnitude. As pointed out by [13] there is an average offset of mas in the Gaia parallaxes and therefore we increased by 0.25 the parallax. According to Gaia DR1, the luminosity as deduced from the flux will be expressed in Gaia units, namely, . The G magnitude, see [14] is
(1)
where is the photometric zero derived as in [15] , we found numerically .
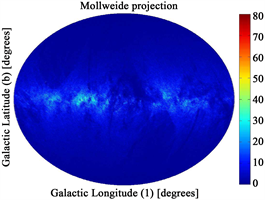
The distribution of all Gaia DR1 sources in the sky is illustrated in Figure 1.
Figure 1. Mollweide projection of the sky density of all Gaia DR1 sources in galactic coordinates.
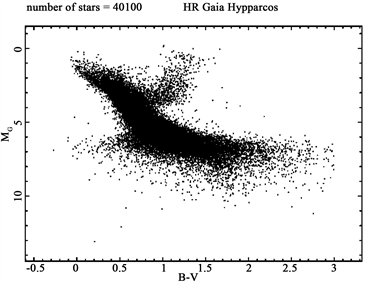
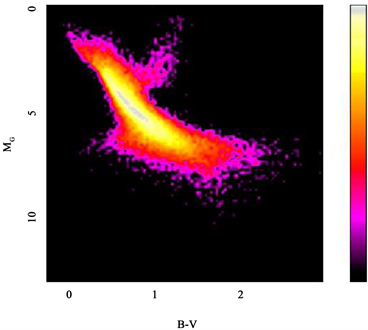
The observational Hertzsprung-Russell (H-R) diagram in as obtained by the Gaia DR1 parallaxes versus (B-V), evaluated as BT-VT, is presented in Figure 2 and in a contour density version in Figure 3, see also figure 1 in [16] .
The distance modulus is
(2)
where is the apparent magnitude in the G-band, is the absolute magnitude in the G-band and d is the distance in pc. Isolating in the above equation we obtain the theoretical curve for the upper observable absolute magnitude
Figure 2. against , evaluated as BT-VT, (H-R diagram) in the first 100 pc.
Figure 3. Contour density of stars for H-R diagram in a logarithmic scale.
(3)
once the maximum apparent magnitude in the g-band, , is inserted, i.e. . Figure 4 presents the absolute magnitude as function of the distance as well the upper theoretical curve in magnitude.
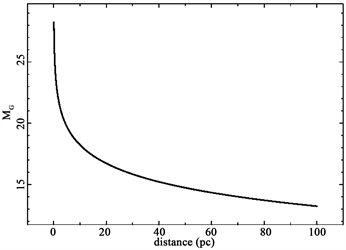
The completeness of the sample can be evaluated by the following relationship for the absolute magnitude
(4)
On inserting in the above formula we obtain a numerical relationship between selected absolute magnitude and numerical relationship over which the sample is complete, see Figure 5.
In the case here considered the absolute magnitude covers the range [3, 12 mag] and therefore we deal with a complete sample.
Figure 4. versus distance in pc in the first 100 pc (green points) and theoretical upper curve in magnitude lower curve in the plot (red line) when .
Figure 5. The relationship of completeness for versus distance in pc.
3. Standard LFs
Here we introduce an algorithm to build the LF, the statistical tests adopted, as well as the Schechter and Gamma LFs. The derived parameter for the local LF will be applied in Section 5.1 according to the general principle that the LF is equal everywhere but the upper observable absolute magnitude decreases with distance.
3.1. The Astronomical LF
A LF for stars is built according to the following points
1) A standard distance is chosen, i.e. 20 pc,
2) The GAIA’s stars are selected according to the following ranges of existence: where is the absolute visual magnitude and ,
3) We organize a histogram with bins large 1 mag,
4) We divide the obtained frequencies by the involved volume,
5) We do not apply the method because our sample is complete at 20pc,
6) The error of the LF is evaluated as the square root of the frequencies divided by the involved volume.
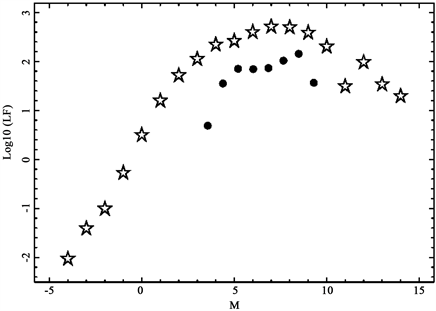
The LF for Gaia’s stars is reported in Figure 6 together the LF main sequence in the V band as extracted from table 2, column 9, in [10] .
3.2. Statistical Tests
The merit function is computed as
(5)
Figure 6. LF in the V band main sequence, empty stars, and Gaia’s LF, filled circles.
where n is the number of bins for the LF of the stars and the two indices theo and astr stand for “theoretical” and “astronomical”, respectively. The reduced merit function is evaluated by
(6)
where is the number of degrees of freedom and k is the number of parameters. The goodness of the fit can be expressed by the probability Q, see equation 15.2.12 in [17] , which involves the number of degrees of freedom and . According to [17] , the fit “may be acceptable” if . The Akaike information criterion (AIC), see [18] , is defined by
(7)
where L is the likelihood function and k is the number of free parameters in the model. We assume a Gaussian distribution for the errors and the likelihood
function can be derived from the statistic where has
been computed by Equation (5), see [19] [20] . Now the AIC becomes
(8)
3.3. The Schechter LF
Let L, the luminosity of a star, be defined in . The Schechter LF of the stars, , originally applied to the stars, see [21] , is
(9)
where sets the slope for low values of , is the characteristic luminosity, and represents the number of stars per pc3. The normalization is
(10)
where
(11)
is the Gamma function. The average luminosity, , is
(12)
An equivalent form in absolute magnitude of the Schechter LF is
(13)
where is the characteristic magnitude.
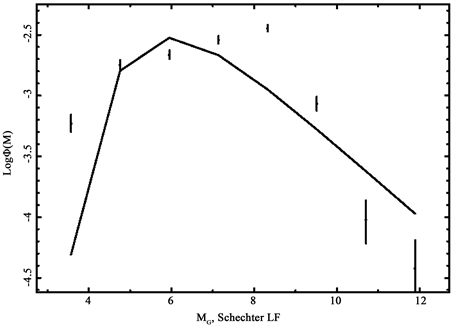
The resulting fitted curve is displayed in Figure 7 with parameters as in Table 1.
Figure 7. The observed LF for stars, empty stars with error bar, and the fit by the Schechter LF when the distance covers the range [0 pc, 20 pc].
Table 1. Parameters of the Schechter LF in the range in distance [0 pc, 20 pc] when
and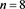 .
.
3.4. The Gamma LF
The Gamma LF, defined in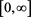 , is
, is
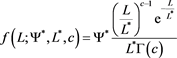 (14)
(14)
where 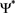 is the total number of stars per pc3,
is the total number of stars per pc3,
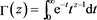 (15)
(15)
where 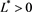 is the scale and
is the scale and 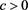 is the shape, see Formula (17.23) in [22] . The average luminosity is
is the shape, see Formula (17.23) in [22] . The average luminosity is
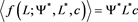 (16)
(16)
The change of parameter 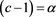 allows obtaining the same scaling as for the Schechter LF (9), for more details, see [23] . The version in absolute magnitude is
allows obtaining the same scaling as for the Schechter LF (9), for more details, see [23] . The version in absolute magnitude is
 (17)
(17)
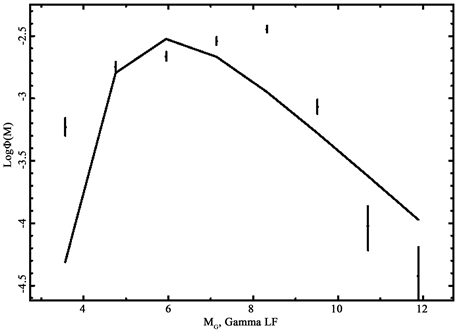
The resulting fitted curve is displayed in Figure 8 with parameters as in Table 2.
4. Truncated LFs
Here we derive the truncated version of the Schechter and Gamma LFs.
4.1. The Truncated Schechter LF
The luminosity L is defined in the interval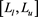

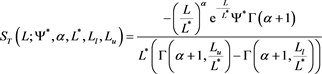
where 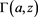
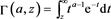
see [24] . The average value is
Figure 8. The observed LF for stars, empty stars with error bar, and the fit by the Gamma LF when the distance covers the range [0 pc, 20 pc].
Table 2. Parameters of the Gamma LF in the range in distance [0 pc, 20 pc] when 
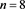
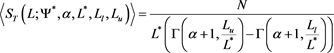
with
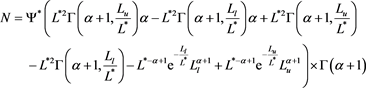
The four luminosities 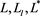
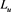
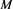
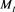

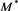
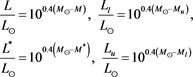
where the indices u and l are inverted in the transformation from luminosity to absolute magnitude and 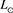

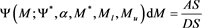
with
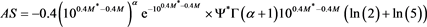
and

The averaged absolute magnitude, 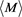
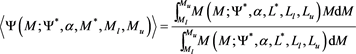
More details can be found in [25] .
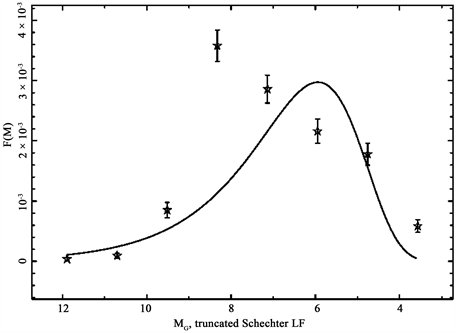
The resulting fitted curve is displayed in Figure 9 with parameters as in Table 3.
Table 3. Parameters of the truncated Schechter LF in the range in distance [0 pc, 20 pc] when 
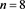
Figure 9. The observed LF for stars, empty stars with error bar, and the fit by the truncated Schechter LF when the distance covers the range [0 pc, 20 pc].
4.2. The Truncated Gamma LF
The truncated Gamma LF is defined in the interval
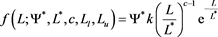
where the constant k is
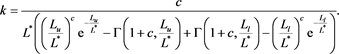
Its expected value is

More details on the truncated Gamma PDF can be found in [23] [26] [27] . The Gamma truncated LF in magnitude is
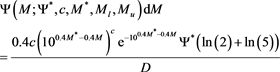
where
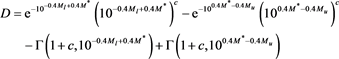
The averaged absolute magnitude, 
The resulting fitted curve is displayed in Figure 10 with parameters as in Table 4.
5. Distance Effects
We model the average absolute magnitude of the stars as a function of the distance, the photometric maximum in the number of stars for a given flux as a function of the distance, and the average distance of the stars for a given flux in the framework of the two truncated LFs here considered.
5.1. Averaged Absolute Magnitude
In order to model the influence of the distance d in pc on the LF, an empirical variable lower bound in absolute magnitude, 
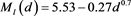
Figure 10. The observed LF for stars, empty stars with error bar, and the fit by the truncated Gamma LF when the distance covers the range [0 pc, 20 pc].
Table 4. Parameters of the truncated Gamma LF in the range in distance [0 pc, 20 pc] when 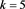

The upper bound, 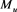
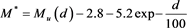
where 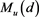
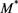
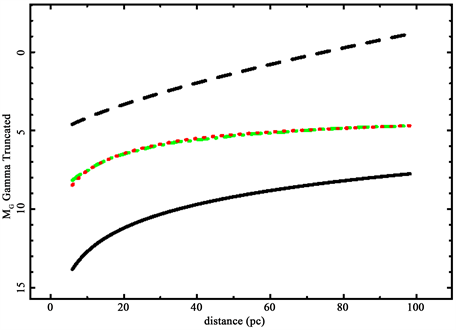
Conversely Figure 12 compares the theoretical average absolute magnitudes for the truncated Gamma LF with the observed ones; also here the value of 
5.2. The Photometric Maximum
The definition of the flux, f, is
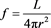
where r is the distance and L the luminosity of the star. The joint distribution in distance, r, and flux, f, for the number of stars is
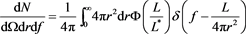
Figure 11. Average observed absolute G-magnitude versus distance for Gaia (green points), average theoretical absolute magnitude for truncated Schechter LF with 
Figure 12. Average observed absolute G-magnitude versus distance for Gaia (green points), average theoretical absolute magnitude for truncated Gamma LF with 
were the factor (
and the Dirac delta function selects the required flux. We now apply the sifting properties of the delta function, see [28] , to the case of the Schechter LF as given by Formula (9)
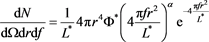
We now introduce the critical radius
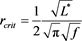
Therefore the joint distribution in distance and flux becomes
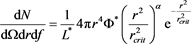
The above number of stars has a maximum at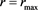
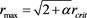
and the average distance of the stars, 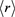
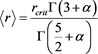
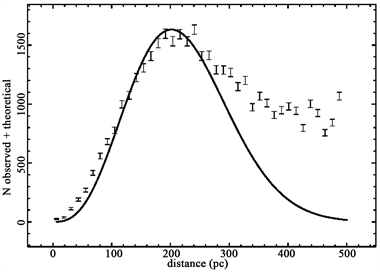
Figure 13 presents the number of stars observed in Gaia as a function of the distance for a given window in the flux, as well as the theoretical curve.
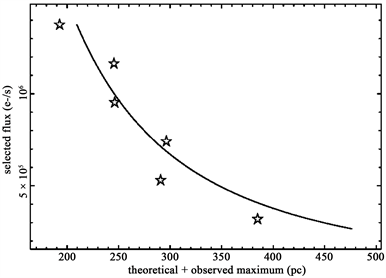
Figure 14 presents the observed position of the maximum of the number of stars as a function of the flux.
Figure 13. The stars of Gaia with 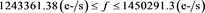

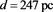
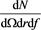
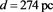
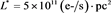
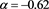
Figure 14. Position of the observed maximum as function of the flux (empty stars) and theoretical average value as given by Equation (40) for the Schechter LF (full line). The parameters are 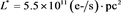
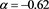
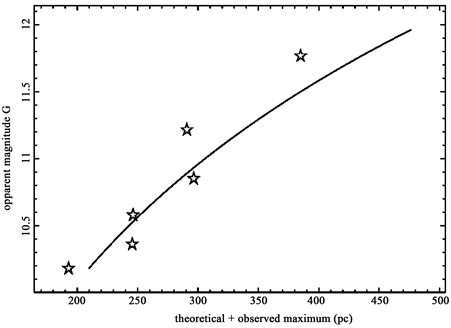
In order to shift to more familiar variables Figure 15 reports the position of the above maximum as function of the apparent Gaia magnitude.
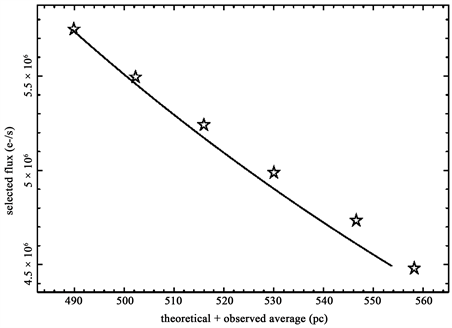
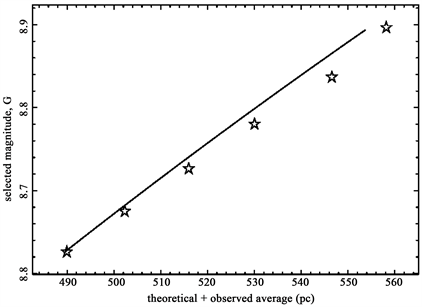
Figure 16 and Figure 17 present the observed average value of the number of stars as a function of the flux and apparent magnitude.
Figure 15. Position of the observed maximum as function of the apparent magnitude, G, (empty stars) and theoretical average value as given by Equation (40) for the Schechter LF (full line). The parameters are the same of Figure 14. Case of the Schechter LF.
Figure 16. Position of the average distance of the stars as function of the flux (empty stars) and theoretical curve as given by Equation (39) (full line) for the Schechter LF. The parameters are 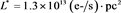
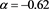
Figure 17. Position of the average distance of the stars as function of the apparent magnitude, G, (empty stars) and theoretical curve as given by Equation (39) (full line) for the Schechter LF. The parameters are the same of Figure 16. Case of the Schechter LF.
In the case of the Gamma LF, the maximum in the number of stars is at
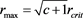
and the average distance of the stars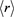
6. Conclusions
Standard LFs: The Schechter function and the Gamma PDF can model the LF for stars, see Table 1 and Table 2 as well as Figure 7 and Figure 8, but the values of the involved parameters depend on the chosen distance.
Truncated LFs: The truncated Schechter function and the truncated Gamma LF can model the averaged absolute magnitude as a function of the distance, see Figure 11 and Figure 12. As an example, four analytical equations have been used in the case of the truncated Schechter LF: 1) the average theoretical absolute magnitude for the truncated Schechter LF, see Equation (26); 2) an empirical expression for the lowest absolute magnitude at a given distance, see Equation (32); 3) a theoretical curve for the highest absolute magnitude at a given distance, see Equation (3); and 4) a distance dependence expression for 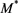
Photometric maximum: The number of stars as a function of the distance presents a maximum which is a function of the flux, see Figure 13 and Figure 14 for the Schechter LF. The theoretical and observed average distance of the stars are also functions of the selected flux, see Figure 16.
Topics not covered: The treatment here adopted deals with a homogeneous distribution of stars and therefore the vertical scale-heights are not covered, see [10] .
Acknowledgements
This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Cite this paper
Zaninetti, L. (2017) Standard and Truncated Luminosity Functions for Stars in the Gaia Era. International Journal of Astronomy and Astrophysics, 7, 255-272. https://doi.org/10.4236/ijaa.2017.74022
References
- 1. Malmquist, K.G. (1920) A Study of the Stars of Spectral Type A. Meddelanden fran Lunds Astronomiska Observatorium Series II, 22, 1.
- 2. Malmquist, K.G. (1922) On Some Relations in Stellar Statistics. Meddelanden fran Lunds Astronomiska Observatorium Series I, 100, 1.
- 3. Malmquist, K.G. (1936) Investigations on the Stars in High Galactic Latitudes II. Photographic Magnitudes and Colour Indices of about 4500 Stars near the North Galactic Pole. Stockholms Observatoriums Annaler, 12, 7.
- 4. Binney, J. and Merrifield, M. (1998) Galactic Astronomy. Princeton University Press, Princeton.
- 5. Butkevich, A.G., Berdyugin, A.V. and Teerikorpi, P. (2005) Statistical Biases in Stellar Astronomy: The Malmquist bias Revisited. MNRAS, 362, 321.https://doi.org/10.1111/j.1365-2966.2005.09306.x
- 6. Eddington, A.S. (1914) Stellar Movements and the Structure of the Universe. Macmillan and Co., London.
- 7. Jaschek, C. and Gomez, A.E. (1985) The Malmquist Correction. A&A, 146, 387.
- 8. Wielen, R. (1974) The Kinematics and Ages of Stars in Gliese’s Catalogue. Highlights of Astronomy, 3, 395. https://doi.org/10.1017/S1539299600002100
- 9. Flynn, C., Holmberg, J., Portinari, L., Fuchs, B. and Jahreiß, H. (2006) On the Mass-to-Light Ratio of the Local Galactic Disc and the Optical Luminosity of the Galaxy. MNRAS, 372, 1149. https://doi.org/10.1111/j.1365-2966.2006.10911.x
- 10. Just, A., Fuchs, B., Jahreiß, H., Flynn, C., Dettbarn, C. and Rybizki, J. (2015) The Local Stellar Luminosity Function and Mass-to-Light Ratio in the Near-Infrared. MNRAS, 451, 149. https://doi.org/10.1093/mnras/stv858
- 11. Gaia Collaboration, Prusti, T., de Bruijne, J.H.J., Brown, A.G.A., Vallenari, A., Babusiaux, C., Bailer-Jones, C.A.L., Bastian, U., Biermann, M., Evans, D.W., et al. (2016) The Gaia Mission. A&A, 595, A1.
- 12. Gaia Collaboration, Brown, A.G.A., Vallenari, A., Prusti, T., de Bruijne, J.H.J., Mignard, F., Drimmel, R., Babusiaux, C., Bailer-Jones, C.A.L., Bastian, U., et al. (2016) Gaia Data Release 1. Summary of the Astrometric, Photometric, and Survey Properties. A&A, 595, A2.
- 13. Stassun, K.G. and Torres, G. (2016) Evidence for a Systematic Offset of -0.25 Mas in the Gaia DR1 Parallaxes. APJ, 831, L6.
- 14. Evans, D.W., Riello, M., De Angeli, F., Busso, G., van Leeuwen, F., Jordi, C., Fabricius, C., Brown, A.G.A., Carrasco, J.M., Voss, H., et al. (2017) Gaia Data Release 1. Validation of the Photometry. A&A, 600, A51.
- 15. Carrasco, J.M., Evans, D.W., Montegriffo, P., Jordi, C., van Leeuwen, F., Riello, M., Voss, H., De Angeli, F., Busso, G., et al. (2016) Gaia Data Release 1. Principles of the Photometric Calibration of the G Band. A&A, 595, A7.
- 16. Van Leeuwen, F., Evans, D.W., De Angeli, F., Jordi, C., Busso, G., Cacciari, C., Riello, M., Pancino, E., Altavilla, G., et al. (2017) Gaia Data Release 1. The Photometric Data. A&A, 599, A32.
- 17. Press, W.H., Teukolsky, S.A., Vetterling, W.T. and Flannery, B.P. (1992) Numerical Recipes in FORTRAN. The Art of Scientific Computing. Cambridge University Press, Cambridge.
- 18. Akaike, H. (1974) A New Look at the Statistical Model Identification. IEEE Transactions on Automatic Control, 19, 716. https://doi.org/10.1109/TAC.1974.1100705
- 19. Liddle, A.R. (2004) How Many Cosmological Parameters? MNRAS, 351, L49. https://doi.org/10.1111/j.1365-2966.2004.08033.x
- 20. Godlowski, W. and Szydowski, M. (2005) Constraints on Dark Energy Models from Supernovae. In: Turatto, M., Benetti, S., Zampieri, L. and Shea, W., Eds., 1604-2004: Supernovae as Cosmological Lighthouses, Vol. 342 of Astronomical Society of the Pacific Conference Series, 508-516.
- 21. Schechter, P. (1976) An Analytic Expression for the Luminosity Function for Galaxies. APJ, 203, 297. https://doi.org/10.1086/154079
- 22. Johnson, N.L., Kotz, S. and Balakrishnan, N. (1994) Continuous Univariate Distributions. 2nd Edition, Vol. 1, Wiley, New York.
- 23. Zaninetti, L. (2016) Pade Approximant and Minimax Rational Approximation in Standard Cosmology. Galaxies, 4, 4. http://www.mdpi.com/2075-4434/4/1/4
- 24. Olver, F.W.J., Lozier, D.W., Boisvert, R.F. and Clark, C.W. (2010) NIST Handbook of Mathematical Functions. Cambridge University Press, Cambridge.
- 25. Zaninetti, L. (2017) A Left and Right Truncated Schechter Luminosity Function for Quasars. Galaxies, 5, 25.
- 26. Zaninetti, L. (2013) A Right and Left Truncated Gamma Distribution with Application to the Stars. Advanced Studies in Theoretical Physics, 23, 1139.
- 27. Okasha, M.K. and Alqanoo, I.M. (2014) Inference on the Doubly Truncated Gamma Distribution for Lifetime Data. International Journal of Mathematics and Statistics Invention, 2, 1.
- 28. Bracewell, R.N. (2000) The Fourier Transform and Its Applications. McGraw-Hill, New York.