International Journal of Astronomy and Astrophysics
Vol.06 No.04(2016), Article ID:72192,9 pages
10.4236/ijaa.2016.64031
Discovery of Light-Light Scattering (A Test of the Primordial Universe)
Nagendra Nath Mondal
Department of Physics, Techno India Batanagar, B-7/360 New Ward, Putkhali, Maheshtala, Kolkata, India

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 28, 2016; Accepted: November 20, 2016; Published: November 23, 2016
ABSTRACT
Different types of scatterings of photons with atoms, theoretical and experimental evidences of the light-light scattering in the visible range of electromagnetic waves are discussed. An inexpensive detection system of scattered light is developed in order to study this phenomenon without considering the scattering cross sections and photon structure function, and results infer that the universe is covered by the mesh of scattered photons. Asymmetry measurement of light-light scatterings shows that lower frequency photon scattered a lot than higher frequency photons. The homogeneity of mesh in absence of a direct incident light is better than that of presence although mesh intensity goes down and up respectively. The recent measurement of gravitational waves from black holes invokes this phenomenon that the primordial forms of the universe are the mesh of scattered light that intensity is extremely low in the absence of stars in a region where they sink is called a black hole.
Keywords:
Black Hole, Electromagnetic Wave, LED, Photodiode, Scattering, Spectroscopy

1. Introduction
A light-light scattering phenomenon in terms of photon-photon scattering is well known where minuscule scattering cross sections are determined. In order to find it, a lot of complex mathematical equations are developed and solved brilliantly by many authors. But none of them had considered yet the colored photon-photon scattering in the visible range of electromagnetic (EM) waves without complex mathematical models and noticed the effect and role of these color photon scatterings on the condition of primordial universe. The basic interest of this research is to create a new meadow of fundamental research in scattering by compiling the colors which will provide a lot of answers of those vital questions relevant with interests of Astrophysics and Astronomy. Many amateur scientists are curious to avoid complex phenomena in order to answer basic questions in the simpler forms. Thus starting from the ABCs of different types of interactions and scatterings, a new physics that is distinct from existing knowledge is demonstrated here. A crucial step toward solving a critical outstanding problem based on theory and experiment is taken into account. Historically a light-light scattering effect is different from the photon-atom interaction or photon-atom/particle scattering (stated in sec. II). The phenomenon which is studied here is neither photon-photon scattering described by Naohiro Kanda [1] nor a Laser-Compton scattering exhibited by J. Urakawa [2] and mechanisms of photon structure function carried out by L3 collaboration at LEP [3] . Heisenberg and Euler have studied the light-light scattering by obtaining Lagrangian density [4] [5] . Applying the modern field theory technique, Kanda has found that the light-light scattering is completely different from the old expression. The reason is basically due to the unphysical condition (gauge condition) which was employed by the QED calculation of Karplus and Neumann [6] [7] [8] [9] . The correct cross section of light-light scattering at low energy (~1 eV that belongs to the visible range of EM wave) is of the order of 10−42 b. However, the calculation by Karplus and Neumann is different since they have put some additional conditions on the QED calculation so as to reproduce the result obtained by Heisenberg and Euler, what is stated by Kanda. None of these determinations include the colored photon-photon scattering phenomena in the visible range of EM waves, so that the studying of it is very crucial that bequeaths significant results for the first time.
2. Theory of Photon-Photon Scattering
2.1. Theory of Photon-Atom Interaction
A number of phenomena can be observed when an energetic photon interacts with atom and the courses are: absorption, spontaneous emission, stimulated emission, photoelectric effect, Auger effect and pair production [10] , those are depicted in Figure 1.
Except the energetic photons, lower energy photons may strike an atom/particle and come back in different directions what is called scattering. A few scattering processes are: Rayleigh scattering, Rutherford scattering, Raman scattering, Compton scattering
(Compton shift which is given by , where θ is the scattering angle
, where θ is the scattering angle
of the photon, see Figure 2(a)) [11] . In this of colored photon-photon scattering a fixed target of atoms/particles are not considered. Instead of that a moving target of light (light is travelling here) is used from a fixed source (LEDs are static) of light (analogous to the inverse Compton scattering) as depicted in Figure 2(b).
2.2. Theory of Colored Light-Light Scattering
Let me presume that two colored photons respectively are blue and red have approached and scattered with different angles θ and φ from each direction of propagation. The intensity and frequency of incident blue photon are Ib and νb respectively; and those of red photon Ir and νr. The intensity of the photons is directly proportional to
Figure 1. Different types of interactions and scatterings are depicted.
Figure 2. (a) Compton scattering and (b) Inverse Compton (light-light) scattering are depicted.
the number of photons (and more appropriately to the square of the amplitude of the EM waves). According to the optical elastic scattering the energy of the incident photon is conserved and its direction is changed only. It is the case when photon is scattered from an atom, e.g., Rayleigh scattering (Figure 1(f)). On the other hand Raman scattering is an inelastic scattering where scattered photon energy (gained from molecules) is higher than the incident photon (Figure 1(h)). The colored light-light scattering is an inelastic process, and hence incident blue photon transfers some of its energy to the incident red photon at the closest approach. Therefore, scattered red photon gains energy from the system after scattering, both elastic (blue photons) and inelastic (red photons) processes have occurred simultaneously, a new brand of scattering phenomena, may be called “Mondal scattering” on the way, and there is a probability of more than one red photon scattering by a single blue photon. Assuming the scattered intensities and frequencies of blue and red photons are  and
and , and
, and 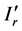 and
and 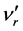 respectively, the scattering formula has been revealed. In the “Mondal scattering” process energy and momentum of photons must be conserved before and after the collision.
respectively, the scattering formula has been revealed. In the “Mondal scattering” process energy and momentum of photons must be conserved before and after the collision.
1) According to the energy conservation law,
 (1)
(1)
where h is a Planck’s constant, subscripts b and r indicate the blue and red light, E and I indicate energy and intensity of photons per unit area and per unit time of the respective colors.
2) According to the law of momentum conservation, moment a of the scattered photons have two components: parallel (cosine) and perpendicular (sine). Hence, (i) cosine component is
 (2)
(2)
where c is the speed of light, and (ii) sine component is
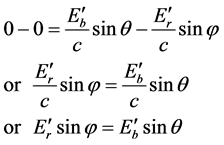 (3)
(3)
Now squaring both sides of Equations (2) and (3) and adding, we have,
 (4)
(4)
Equating Equations (1) and (4) we have,
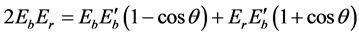 (5)
(5)
A few cases can be considered: (i) θ = 0, (then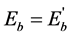 ), (ii) θ = π, (then
), (ii) θ = π, (then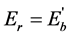 ), and (iii) when
), and (iii) when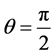 , Equation (5) reduces to,
, Equation (5) reduces to,
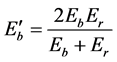 (6)
(6)
Now Equating Equations (1) and (6) we have
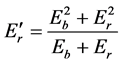 (7)
(7)
When the light incident on the surface of a photodiode (detail of it can be found elsewhere [12] [13] ), it can produce current (i) and voltage (V = iR, where R is the resistance of Multi-meter circuite) which is directly proportional to the incident energy (and energy is proportional to the intensity), i.e.,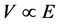 . Therefore, Equations (6) and (7) can be modified respectively in the following form
. Therefore, Equations (6) and (7) can be modified respectively in the following form

And

We can calculate the asymmetry (A) between the scattered blue and red photons from Equations (8) and (9) in the following form,

(In order to avoid much mathematical complication elastic scattering process are taken into account, because determination of scattered frequencies are not possible in the following experimental detection system).
or 
Experimentally parameters in the r.h.s. of Equations (10) and (11) are achievable and hence asymmetries are to be obtained.
3. Experiments
3.1. Detector Developments
In order to determine the asymmetry (A) of the colored light a “+” shape experimental apparatus is constructed whose lay-out is illustrated in Figure 3. The length of each arm is 6 cm and diameter is φ = 1.2 cm which are made of steel pipes. Inner surface of the pipe is covered with black paper for the reduction of light-scattering effect. Different colored light emitting diodes (LEDs, detail of it can be found elsewhere [14] ) are used for the source of incident lights and fixed them face to face by using wooden corks at each end of the pipe. The area of a semi-spherical surface of a LED is about 8π mm2. Similarly two photodiodes (PDs, model: BPW 34) sensors are used face to face in order to measure the intensity of the scattered light in terms of voltage by connecting with a digital multimeter. The surface area of each PD is about 4 mm2.
3.2. Experimental Methods and Results
First the voltages of the incident colored photons in pair are detected individually by each PD. Then PDs are changed from this direct measurement position to the perpendicular positions of each incident colored photon. Then background effect is measured independently of each color on/off conditions and data are subtracted from the data of scattered photons during the analysis. The background arises due to light scattering with air molecules and inner surface of the beam pipe. The experiments are executed in pair of colors with respect to blue only. The results of different colored photons (Row 1 - 4) in pairs are put in order in Table 1. Similarly for the studying of mesh of light-light scattering direct incident light L-1 and L-2 are detected respectively by PD-1 and PD-2 sensors just by removing the sources of color light and coving the mesh light of the room into the beam pipes.
Figure 3. Experimental apparatus for light- light scattering.
Table 1. Experimental results.
Then PD-1 and PD-2 sensors are perpendicularly set-up and detected scattered photons. The system is oriented 90 degree and repeating the previous steps again. The average data are tabulated in Row-5 and their asymmetries are calculated. Now the whole system is brought outside in a sunlit area and incident and scattered light are detected as well which are also shown in Row-6. Percentage of errors of columns (vi) and (vii) are estimated from the respective data of columns (iv) and (v). The error of scattered asymmetry (row 5, column vii) is bigger than any other calculated values because statistical data (row 5, column v) are inferior to any other rows.
4. Discussions
Average frequency of each colored LED is shown in Table 1 (column iii) and corresponding incident (column iv) and scattered (column v) energies in terms of voltages are revealed also. Using Equations (10) and (11) asymmetries are calculated (column vi, vii). When the ratio of energies of the scattered photons is taken into account in order to find Asc it is found that Asc is different from the calculated Ain, because number of incident and scattered photons of individual colors are different. In principle Ain and Asc are the same; hence optimization is required that shows the corresponding scattered photon numbers in the last column (viii). Those photons numbers are synchronized according to the observed values of column (v). The results infer that higher frequency photons scattered less than lower frequency photons, because some of the energy of higher frequency photons are transferred to the lower frequency photons. This is a vital surveillance of this study and asymmetries crop up due to this fact. It point out the basic distinctions from other scatterings which are stated in the introduction and in sec. 2.1. Significantly greens are scattered less than reds by blue photons.
In Figure 4, theoretical calculations of asymmetries among different colors (frequency range of blue (606 - 660) THz, green (526 - 606) THz, yellow (508 - 535) THz, orange (480 - 507) THz and red (400 - 480) THz) with blue one are depicted. In simulation, the number of photons of incident colors is considered to be the same and found that
Figure 4. Asymmetry spectrum (theoretical and experimental).


The study of experimental light-light scattering phenomena is vital in order to understand the state of the early universe. Hence asymmetries of light-light scattering mesh are studied inside the room (row-5) and outside of the room (row-6). This result shows that the sources of light of our surroundings are the mesh of scattered light in absence of the direct incident light source also. It means that dark can never be dark completely; an ideal situation of the primordial universe when there was no stars except mesh of the invisible scattered photons and the fifth state of matter [15] . Recent finding of direct gravitational wave from binary black holes explores this situation [16] . We can’t see anything because the intensity of the scattered light is not good enough to make any sense in our eyes what is painted as a black hole. For a precision measurement of “Mondal Scattering” effect highest intense colored source, large scattering chamber and pipes with ultrahigh vacuum system and detectors of large solid angle (consist of colored PDs) are required which is my future work.
5. Conclusion
A light-light scattering chamber is constructed in order to study the asymmetry of the scattering in the visible range of EM waves. Asymmetry of the measurement shows that higher frequency colored photon scattered less than lower frequency photon and light- light scattered mesh exists everywhere, a trial of primitive universe. The homogeneity of the scattered mesh is better in the absence of stars, the ideal situation of a black hole.
Acknowledgements
Author is pleased to acknowledge the financial support from his family for this project and to perform the research in the in-house laboratory. Paper publication fee is partially received from the institute.
Cite this paper
Mondal, N.N. (2016) Discovery of Light-Light Scattering (A Test of the Primordial Universe). International Journal of Astronomy and Astrophysics, 6, 384-392. http://dx.doi.org/10.4236/ijaa.2016.64031
References
- 1. Kanda, N. Light-Light Scattering.
http://arxiv.org/pdf/1106.0592.pdf - 2. Urakawa, J. Laser-Compton Scattering at ATF.
http://pfwww.kek.jp/pf-seminar/ERL/presen/urakawa.pdf - 3. Achard, P., et.al. (2005) L3-Collaboration, Measurement of the Photon Structure Function Fγ2 with the L3 Detector at LEP. Physics Letters B, 622, 249-264.
https:/doi.org/10.1016/j.physletb.2005.07.028 - 4. Euler, H. and Kockel, B. (1935) über die Streuung von Licht an Licht nach der Diracschen Theorie. Naturwissenschaften, 23, 246-247.
https:/doi.org/10.1007/BF01493898 - 5. Euler, H. (1936) über die Streuung von Licht an Licht nach der Diracschen Theorie. Annalen der Physik, 418, 398-448.
https:/doi.org/10.1002/andp.19364180503 - 6. Heisenberg, W. and Euler, H. (1936) Folgerungen aus der Diracschen Theorie des Positrons. Zeitschrift für Physik, 98, 714-732.
https:/doi.org/10.1007/BF01343663 - 7. Berestetskii, V.B., Lifshitz, E.M. and Pitaevskii, L.P. (1974) Relativistic Quantum Theory. Pergamon Press, Oxford, 9.
- 8. Karplus, R. and Neuman, M. (1950) Non-Linear Interactions between Electromagnetic Fields. Physical Review, 80, 380.
https:/doi.org/10.1103/PhysRev.80.380 - 9. Karplus, R. and Neuman, M. (1951) The Scattering of Light by Light. Physical Review, 83, 776.
https:/doi.org/10.1103/PhysRev.83.776 - 10. Rohlf, J.W. (1994) Modern Physics from α to Zo. John Wiley & Sons, Inc., New York, 350-352.
- 11. Beiser, A. (1987) Concepts of Modern Physics. McGraw-Hill Book Company, Singapore, 71-74.
- 12. Mondal, N.N. (2014) Versatile Nature of the Earth Causes Disasters. Journal of Environmental Research and Development, 9, 75-82.
- 13. Mondal, N.N. (2014) Study Chromaticity Solar Spectrum. Journal of Astronomy & Astrophysics, 4, 510-518.
https:/doi.org/10.4236/ijaa.2014.43047 - 14. Mondal, N.N. (2014) Discovered Solar Positronium. Journal of Astronomy & Astrophysics, 4, 620-627.
https:/doi.org/10.4236/ijaa.2014.44057 - 15. Mondal, N.N. (2015) Does the Fifth State of Matter Originate the Early Universe? Journal of Physical Science and Application, 5, 407-414.
- 16. Abbott, B.P., et. al. (2016) Observation of Gravitational Waves from a Binary Black Hole Merger. Physical Review Letters, 116, 061102-1-16.






