International Journal of Astronomy and Astrophysics
Vol.05 No.04(2015), Article ID:62107,9 pages
10.4236/ijaa.2015.54029
Calculations for Density of Quark Core Consisting of Mono Flavored Closely Packed Quarks inside Neutron Star
Jehangir A. Dar1*, Pawan Kumar Singh2, Ram Swaroop3
1Plasma Waves and Particle Acceleration Laboratory, Department of Physics, Indian Institute of Technology Delhi, New Delhi, India
2Department of Physics, ARSD College, University of Delhi (South Campus), New Delhi, India
3North Bengal Science Centre, National Council of Science Museums, Ministry of Culture, Government of India, Siliguri, India

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 22 February 2015; accepted 17 December 2015; published 22 December 2015
ABSTRACT
The attempt has been taken to calculate the density of stars possessing quark matter core using sphere packing concept of crystallography. The quark matter has been taken as solid in nature as predicted in references 36 and 37, and due to immense gravitational pressure at the core of the star the densest packing of quarks as spheres has been assumed to calculate the packing fraction Φ, thus the density r of the matter. Three possible types of pickings―mono-sized sphere packing, binary sphere packing and ternary sphere packing, have been worked out using three possible types of quark matter. It has been concluded that no value about the r of quark matter can be calculated using binary and ternary packing conditions and for mono-sized packing condition different flavor quark matters of different values in the density have been calculated using results from the experiments done by HI, ZEUS, L3 and CDF Collaborations about the radius limit of quark. For example, for u quark matter r ranges from 4.0587 × 1048 - 7.40038 × 1048 MeV/c2 cm3 using results of L3 Collaboration, for s quark matter 15.91794 × 1048 - 17.6866 × 1048 MeV/c2 cm3, etc.
Keywords:
Neutron Star, Packing Fraction, Quark Matter, Quark Gluon Matter, Kepler’s Conjecture Theorem, Neutron

1. Introduction
Neutron stars are one of the densest stars known in the cosmos. They are formed by the gravitational collapse of some massive stars having inner core mass above Chandrasekhar limit―1.4 Mo [1] , but with mass lesser than the mass required to overcome neutron degeneracy pressure. The neutron degeneracy pressure is the pressure caused by degenerate neutron gas [2] . There is also a limit for neutron star above which the stars are said to form black hole [3] [4] which is a region of space time from which nothing can escape to infinity as predicted by General theory of relativity [5] . Up to 1967 the idea of neutron star was only theoretical but after the discovery of pulsar PSR B1919 + 21 by Joceyln Bell Burnell and Antony Hewish on November 28, 1967 [6] , the idea was taken seriously. Pulsar is not more than a rotating neutron star that emits regular beams of electromagnetic radiation. Different scientists suggest different densities of the core of neutron star. The neutron star’s density ranges from 1 × 1017 Kg/m3 in the crust―exceeding with the depth―to above 6 × 1017 - 8 × 1017 g/m3 that is denser than an atomic nucleus [7] [8] . We can say that the density of the core of neutron star is still mystery; it is still an unsolvable question in physics. In this paper to some extent this mystery has been tried to solve.
Moving towards its core composition of super dense matter, the composition of the matter is uncertain. According to different models it may be liquid or solid. One of the models says the core consists of super fluid- neutron―degenerate matter formed mostly by neutrons with some exceptions of protons and electrons [9] . One another say, it consists of strange-degenerate matter including strange quarks in addition to up and down quarks [10] . While, some theorize it consists of high energy pions and kaons in addition to neutrons [6] or ultra-dense quark-degenerate matter [11] . What actually exists inside core is not yet known absolutely we are having only some models based on whom density of core of neutron star is calculated. The actual density will remain uncertain as long as we are not certain about its composition. In fact, this is one of the prominent reasons why the picture about the limiting mass of neutron star remained unclear from more than seventy years even after the pioneering attempt taken by Oppenheimer and Volkoff [12] .
Between the neutron stars and black holes it has been theorized that there remains one more type of neutron star commonly called as quark star. The mass of quark star falls between mass limit of neutron star and the minimum mass required for the star to become black hole. The whole idea of quark star is hypothetical and no strong confirmation has been observed about the presence of such stars, but the observations taken on stars like RX JI856.5-3754 and 3C58 suggest these stars to be quark stars due to available density above the density prescribed for neutron stars [13] . There are also some suggestions about the presence of quark star like the stars PSR B0943 + 10, SN2006gy, SN2005gj, SN2005ap and SN1987 [14] . Quark stars get formed when the mass of star is sufficient to create gravitational pressure above the degeneracy pressure caused by neutrons inside the star. Under such conditions neutrons can break into their constituent particles, that is, quarks create quark matter [15] . The matter will consist of up and down quarks―symbolized as u for up quark and d for down quark. However, the quark matter with some composition of strange s quarks, or of other different compositions is also possible.
It is theorized that neutron stars consisting core of ordinary quark matter, that is, u and d quark matter is stable, under extreme temperatures or pressures. However, quark stars consisting entirely of this ordinary quark matter are highly unstable and therefore dissolve spontaneously in another kind of quark matter commonly called as strange quark matter [13] [16] . Such type of stars possessing this strange quark matter is called as strange quark star [16] . Strange quark or s quark is the 3rd lightest quark in the quark family. It is mostly found in hadrons like kaons (k), sigma baryons (Σ), strange D mesons (D) and some other strange particles like the white dwarfs’ and neutron stars. The quark star’s gravitational collapse is controlled by quark degeneracy pressure since the quarks belong to fermions family like electrons and neutrons and thus obey Pauli’s exclusion principle. In the paper we will use the fact what is possible when the gravitational pressure will exceed the Pauli’s exclusion principle. The idea that they will turn into the densest packing system is used here in the paper.
Now let us move to another important aspect of the paper, that is, sphere packing in crystallography. Sphere packing is a possible regular or irregular arrangement of similar or dissimilar spheres in any volume. The spherical packing in 3-dimensional Euclidean space is very common. Basically there are two known arrangements of spheres known these are regular or lattice arrangement and irregular or random arrangement. FCC (face centered cubic) or CCP (cubic close packing) and HCP (hexagonal close packing) are the two unit structures known possible in the close packing of spherically symmetrical and mono sized particles. These two structures have the highest packing density as proved by Gauss in 1831 and originally proposed by Johannes Kepler in 1611 in his so called Kepler’s conjecture theorem [16] [17] . The highest average atomic packing function (APF) Φ possible due to Keplers’ Conjecture theorem is 0.74048048 [4] [18] . However, this value validates only to mono sized sphere packing. This conjecture was further proved by Thomas Callister Hales, following the suggested ideas of Laszlo Fejes Toth. In both the FCC and HCP packing each sphere has twelve neighbors. There is one gap surrounded by six spheres (octahedral) and two smaller gaps surrounded by four spheres (tetrahedral).
For close packing of two or more different sized spheres, to calculate the Φ becomes much difficult. Now the APF Φ becomes function of radius ratio between the spheres and sphere concentration over other sized concentrations, like for binary sphere packing the small sphere concentration in the mixture is calculated. Different methods like Monte Carlo [19] - [21] , genetic algorithms [22] and TJ sphere packing algorithm [23] , have been applied to attempt to find binary sphere packaging over certain ranges of functions α and χ [19] . There is no clear conjecture as to which structures are the densest at different radius ratios. Structures are known which exceed the close packing density for radius ratios up to 0.659786 only [19] . For what structures are possible with radius ratios above 0.659786 we don’t have any idea about it, no work has been done about it. In binary sphere packing of mono sized spheres it is possible to get the packing density more than Kepler’s Conjecture density, that is, 0.74048, if small spheres up to 0.29099 of the radius of the larger sphere are inserted into the vacant voids between the larger spheres [18] .
In the paper we are using the same (mono) sized sphere packing and binary sphere packing concepts to to solve the problem to some extent. A one more packing of three sized spheres which we can call ternary sphere packing has been included about which no work has been yet done. This paper is the preceding paper of previous paper of author Jahangir Ahmad Dar which came in IJAA read reference No. 4 regarding the technique used in the paper to derive value of density. In the previous paper neutrons where taken as spheres and here quarks. We can say this is the second work done on the technique, that is, use of sphere packing in astronomy to derive density of stars.
2. Calculations of Density of Quarks Core of Neutron Star
Different models of neutron star matter suggest different forms and types of quark matter inside the core of the neutron star. However, there is not any form/state of any type of quark matter known of which the exact mass density ρ has been calculated. So the density of core of neutron star has remained a mystery. Here we will use the packing fraction concept well known in crystallography, to discuss and calculate the possible packing and thus the mass density ρ of quark matter inside the core of neutron star. We will try to solve the density by considering three possible solid quark matter types that are possible to exist in the core of the star.
2.1. Binary Sphere Packing to Sought Out Density
It is well known that neutron stars are balanced by neutron degeneracy pressure [3] [24] [25] . And at some depth particularly at the core of the neutron star, the gravitational inward pressure is so high such that neutrons will disintegrate in to their constituents u and d quarks. The formed quark matter will consist of u and d quarks by considering the mass of gluons that held the quarks together inside proton or neutron as zero [26] .
If n is the number of neutrons that has crushed down to form quark matter occurring volume V then the total number of quarks available in the volume V is 3n, since each neutron contributes 3 quarks-1 u quark and 2 d quarks to the quark matter. The ratio between total number of u quarks and d quarks in volume V will be equal to the ratio between u quarks and d quarks occupying a single neutron, i.e.,
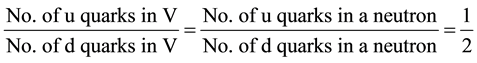 (1)
(1)
Similarly, in any structure or unit cell created by this binary quark matter, the ratio between u and d quarks occupying the cell must be same , i.e.,
, i.e.,
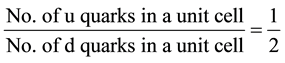 (2)
(2)
The packing density of this quark matter depends on functions α and χ, i.e., radius ratio between the quarks and the sphere concentration [27] . For any packing of spheres not necessarily identical in size, packing fraction is given by
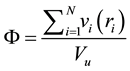 (3)
(3)
where 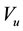 is the volume occupied by the cell,
is the volume occupied by the cell,  is the volume of the ith quark with radius
is the volume of the ith quark with radius 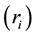 and is given as
and is given as
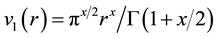 (4)
(4)
where Г is Euclid’s function.
To calculate the χ we must calculate the d quark concentration in the matter as they are lesser in size than u quark. If k is the number of u quarks in the cell therefore as per u and d number ratio indicated in the Equation (2), the number of d quarks will be 2k. Thus we have for small sphere concentration in a case as
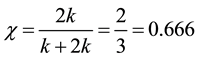 (5)
(5)
on the basis of mass difference between u and d quarks we have assumed that they possess different sizes therefore have different radii. However, at this present stage we don’t have any data nor have been done any work regarding sizes of quarks. So it is impossible to know anything about the value of function α and the biggest problem is that we can’t even assume or guess it, so that to use it in deriving the partition function of binary quark matter. Therefore by considering the densest solid core of neutron stars as the quark matter possessing u and d quark flavors with different sizes it is impossible to calculate the density of the core or matter using any crystallography technique. The problem will be same for any other flavored quark matter as per no size of any type of quark is known yet.
2.2. Ternary Sphere Packing to Sought out Density
In standard model of the particles, neutron consist of three quarks binding together by the exchange of force carrying particles called as gluons symbolized by g. Gluons are the force carrying particles which carry simultaneously color and anticolor and couple to the color charge. In theoretical predictions the mass of gluon, mg is taken as zero [28] , therefore in the above condition we have assumed the core consisting of quark matter only. However by some work referenced as 29, 30, 31 it is predicted that gluons indeed have some mass limits. Some of mg predictions are 1 MeV, 20 MeV, 500 MeV, 370 MeV, etc. [29] - [31] . Since it is clear from different predicted values of mg the actual value of mg is still a mystery but it is clear that mesons have some mass and its contribution to any matter can’t be neglected like in the case for the crushed and deformed neutrons under the effect of gravitational pressure inside the neutron star to form quark matter. The matter will associate mesons as third kind of solid spheres possessing some value of mg therefore possess some volume. The matter therefore will be quark-gluon matter. If the state of matter is taken solid [32] [33] as taken in the previous case and close packing of quark-gluon is considered as is possible due high gravitational pressure. The packing problem will be now ternary sphere packing. For ternary case we don’t have any solution and procedure to estimate the packing density therefore to calculate the mass density of quark-gluon matter. The main problem in crystallography to sought out before using the packing fraction of matter to calculate mass density of densest quark-gluon matter are:
1. What is the impact on function radius ratio α when there are more than two different sized spheres used for packing or how will α behave for ternary sphere packing.
2. We don’t know radius of gluon even the gluon mass is not known well.
3. We can calculate any sized sphere concentration χ in a any mixture by expanding Equation (5) as
 (6)
(6)
but the effect by other sized spheres on the structure of the cell is not known.
4. No structure is known consisting any ternary sphere packing.
A new method is required to invent for this discussed ternary sphere packing or to solve any ternary sphere packing in any branch of science. In a nutshell by considering gluon as a massive particle and its significant contribution in creating quark-gluon mass for any solid and close packing possible inside any star like neutron star, at this era it is impossible to calculate its packing density and therefore to calculate mass bound inside the region consisting quark-gluon matter, that is the core of neutron star. At this time we can suggest only that the density packing fraction for quark-gluon matter inside the star will be higher than Kepler’s limit or any greatest known packing density in binary sphere packing if the radius of gluon and the number of gluons will be sufficient to fill every vacant void formed between the packing of u and d quarks as shown in Figure 1 below, by supposing that the radius or size of u quark, d quark and g gluon varies as they vary in masses.
In the figure, the small spheres are considered as gluons g, big sized spheres as u quarks and the remaining sized as d quarks. In the image where the gluon concentration is higher than other regions indicates the void vacancy created by packing of u and d quarks is higher than other voids.
2.3. Mono Sized Sphere Packing to Sought out Density
Since we have not been able to calculate the density by considering the quark matter inside the core of the neutron star as a binary sphere packing and ternary sphere packing, we can consider the problem as mono sized spherical quark problem which is the only option for us at this time to imagine the density of the matter in the core of neutron star.
Now the value of α in this case becomes 1 called as Kepler’s limit [27] . Due to the gravitational collapse the quarks will take highest possible packing fraction, which according to Kepler’s Conjecture Theorem is Φ = 0.740480 [17] [27] . So the possible structures constituting the said Kepler’s limits will be FCC and CCP. The basic structure of FCC and HCP is shown in Figure 2 as below.
The images above has been taken from the previous work done by the author Jahangir A.D. on neutron stars in the paper ‘’Mass limit of neutron star’’ see reference no. 4.
In both structures coordinate number is 12 and both have the same packing fraction [17] [27] , therefore we can take any structure to calculate the mass density obtained by the quark matter. Take HCP as a unit cell. The
Figure 1. Schematic of quarks-gluons packing.

Figure 2. (a) HCP unit cell; (b) FCC unit cell.
mass of this unit cell indicated as M is the total mass of the quarks available in the cell, that is,
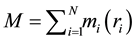 (7)
(7)
where, N is the number of quarks which is 6 and m is the mass of the individual quark.
The densest available packing fraction for HCP and FCC as per Kepler’s Conjecture Theorem is 0.74048…
Rearranging Equation (3), we get
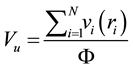 (8)
(8)
But
Putting the values of 



where F = 0.74048. By taking value of × as 3 in Equation (4), that is, considering whole case as a 3-dimensional, we have

Therefore, we have

It is clear that the density of quark matter or the core of neutron star depend on two functions m and r, that is,
Using the above mentioned values in the Equation (11), we have calculated different possible values about the density of mono sized quark-matter and are given in the following Table 1.
In the table 












The density of mono-sized densest packing quark matter will be somewhere between the ranges predicted in the tables as per the limits in radii of quark particles predicted by some successful experiments in the world. The values predicted in the tables are the only values we can consider about the density of densest mono-sized quark matter that is believed to be is available inside the core of neutron stars. In the strange stars like quark stars it is possible at different layers these all densities are possible
3. Conclusion
We have used packing fraction concept to derive the density of quark matter inside neutron stars. We studied the three cases possible for quark type concentration―mono-sized single flavor packing of quark matter, binary sized u and d flavor packing of quark matter and u and d quark with gluon as ternary sphere packing. Among the all three cases we have concluded that only density of mono-sized case is possible to calculate density ranges
Table 1. Calculated density of mono sized quark-matter.
Table 2. Range of mass density of monosized quark-matter.
between two values for every experimental value about the radius of quark predicted by the work of four known Collaborations―HI, ZEUS, L3 and CDF.
Cite this paper
Jehangir A.Dar,Pawan KumarSingh,RamSwaroop, (2015) Calculations for Density of Quark Core Consisting of Mono Flavored Closely Packed Quarks inside Neutron Star. International Journal of Astronomy and Astrophysics,05,258-266. doi: 10.4236/ijaa.2015.54029
References
- 1. Chandrashekhar, S. (1931) The Maximum Mass of Ideal White Dwarfs. Astrophysical Journal, 74, 81.
- 2. Potehin, A.Y. (2011) The Physics of Neutron Stars.
http://arxiv.org/pdf/1102.5735.pdf - 3. Srinivasan, G. (2002) The Maximum Mass of Neutron Stars. The Astronomy and Astrophysics Review, 11, 67-96.
http://dx.doi.org/10.1007/s001590200016 - 4. Jahangir, A.D. (2014) Mass Limit of Neutron Star. International Journal of Astronomy and Astrophysics, 4, 414-418.
http://dx.doi.org/10.4236/ijaa.2014.42036 - 5. Wald, R.M. (1997) Gravitational Collapse and Cosmic Censorship.
http://arxiv.org/abs/gr-qc/9710068 - 6. Backer, D.C. (1976) Pulsar Average Wave Forms and Hollow-Cone Beam Models. Astrophysical Journal, 209, 895-907.
http://dx.doi.org/10.1086/154788 - 7. Schafner, J. and Mishustin, I.N. (1996) Hyperon-Rich Matter in Neutron Stars. Physical Review C, 53, 1416.
- 8. Miller, M.C. (2004) Introduction to Neutron Stars. University of Maryland, College Park.
- 9. Villian, L. and Haensel, P. (2008) Astron. and Astrophys, 444, 539.
- 10. Farhi, E. and Jaffe, R.L. (1984) Strange Matter. Physical Review D, 30, 2379-2390.
http://dx.doi.org/10.1103/PhysRevD.30.2379 - 11. Haensel, P., Potekhin, A.Y. and Yakovlev, D.G. (2007) Neutron Stars. Springer, Berlin.
http://dx.doi.org/10.1007/978-0-387-47301-7 - 12. Oppenheimer, J. R. and Volkoff, G. M. (1939) On Massive Neutron Cores. APS Journals, 55, 374.
- 13. Drae, J.J., Marshall, H.L., Dreizler, S., et al. (2002) Is RX J185635-375 a Quark Star? Astrophysical Journal, 572, 996-1001.
http://arxiv.org/abs/astro-ph/0204159 http://dx.doi.org/10.1086/340368 - 14. Chan, T.C., Cheng, K.S., Haro, T., Lau, H.K., Lin, L.M., Suen, W.M. and Tian, X.L. (2009) Could the Compact Remnant of SN 1987A Be a Quark Star? Astrophysical Journal, 695, 732-746.
http://dx.doi.org/10.1088/0004-637X/695/1/732 - 15. O’Toole, P.I. and Hudson, T.S. (2011) New High-Density Packings of Similarly Sized Binary Spheres. The Journal of Physical Chemistry C, 115, 19037-19040.
http://dx.doi.org/10.1021/jp206115p - 16. Weber, F., et al. (1994) Strange-Matter Stars. In: Proceedings: Strangeness and Quark Matter, World Scientific, Singapore, 87.
- 17. Hales, T.C. (2005) A Proof of the Kepler Conjecture. Annals of Mathematics, 162, 1065-1185.
http://dx.doi.org/10.1088/0954-3899/33/1/001 - 18. Zong, C. (2002) From Deep Holes to Free Planes. Bulletin of the American Mathematical Society, 39, 533-555.
http://dx.doi.org/10.1090/S0273-0979-02-00950-3 - 19. Shapiro, S.L. and Teukolsky, S.A. (2008) Black Holes, White Dwarfts and Neutron Stars: The Physics of Compact Objects. Wiley, New York.
- 20. Filion, L., Marechal, M., van Oorschot, B., Pelt, D., Smallenburg, F. and Dijkstra, M. (2009) Efficient Method for Predicting Crystal Structures at Finite Temperature: Variable Box Shape Simulations. Physical Review Letters, 103, Article ID: 188302.
- 21. Kummerfeld, J.K., Hudson, T.S. and Harrowell, P. (2008) The Densest Packing of AB Binary Hard-Sphere Homogeneous Compounds across All Size Ratios. Journal of Physical Chemistry B, 112, 10773-10776.
http://dx.doi.org/10.1021/jp804953r - 22. Filion, L. and Dijkstra, M. (2009) Prediction of Binary Hard-Sphere Crystal Structures. Physical Review E, 79, Article ID: 046714.
http://dx.doi.org/10.1103/physreve.79.046714 - 23. Torquato, S. and Jiao, Y. (2010) Robust Algorithm to Generate a Diverse Class of Dense Disordered and Ordered Sphere Packings via Linear Programming. Physical Review E, 82, Article ID: 061302.
http://dx.doi.org/10.1103/physreve.82.061302 - 24. Lattimer, J.M. and Prakesh, M. (2004) The Physics of Neutron Stars. Science, 304, 536-542.
http://arxiv.org/abs/astro-ph/0405262 http://dx.doi.org/10.1126/science.1090720 - 25. Baym, G. and Pethick, C. (1979) Physics of Neutron Stars. Annual Review of Astronomy and Astrophysics, 17, 415-443.
http://dx.doi.org/10.1146/annurev.aa.17.090179.002215 - 26. Yao, W.M., et al. (2006) Review of Particle Physics: Neutrino Mass, Mixing, and Flavor Change. Journal of Physics G, 33, 1-1232.
http://dx.doi.org/10.1088/0954-3899/33/1/001 - 27. Hopkins, A.B. and Stillinger, F.H. (2012) Densest Binary Sphere Packings. Physical Review E, 85, Article ID: 021130.
http://dx.doi.org/10.1103/physreve.85.021130 - 28. Nave, R. (2008) Quarks. HyperPhysics. Georgia State University, Department of Physics and Astronomy, Atlanta.
- 29. Halzen, F., Krein, G. and Natale, A.A. (1993) Relating the QCD Pomeron to an Effective Gluon Mass. Physical Review D, 47, 295.
http://dx.doi.org/10.1103/PhysRevD.47.295 - 30. Cornwall, J.M. and Soni, A. (1983) Glueballs as Bound States of Massive Gluons. Physics Letters B, 120, 431-435.
http://dx.doi.org/10.1016/0370-2693(83)90481-1 - 31. Yndurain, F. (1995) Limits on the Mass of the Gluon. Physics Letters B, 345, 524-526.
http://dx.doi.org/10.1016/0370-2693(94)01677-5 - 32. Yu, M. and Xu, R.X. (2011) Toward an Understanding of Thermal X-Ray Emission of Pulsars. Astroparticle Physics, 34, 493-502.
http://dx.doi.org/10.1016/j.astropartphys.2010.10.017 - 33. Dai, S. and Xu, R.X. (2012) Quark-Cluster Stars: Hints from the Surface.
http://arxiv.org/pdf/1201.3759.pdf - 34. ZEUS Collaboration (2004) Search for Contact Interactions, Large Extra Dimensions and Finite Quark Radius in ep Collisions at HERA. Physics Letters B, 591, 23-41. http://dx.doi.org/10.1016/j.physletb.2004.03.081
- 35. Truemper, J.E., Burwitz, V., Haberl, F. and Zavlin, V.E. (2004) The Puzzles of RX J1856.5-3754: Neutron Star or Quark Star? Nuclear Physics B Proceedings Supplements, 132, 560-565.
http://dx.doi.org/10.1016/j.nuclphysbps.2004.04.094 - 36. Chekanov, S., Derrick, M. and Krakauer, D. (2003) Argonne National Laboratory, Chicago (And Others); Deutsches Elektronen-Synchrotron (DESY), Hamburg; ZEUS Collaboration, IAEA, INIS, 35032556.
- 37. Oerter, R. (2006) The Theory of Almost Everything: The Standard Model. Penguin Group, London.
NOTES
*Corresponding author.





