International Journal of Astronomy and Astrophysics
Vol.4 No.2(2014), Article ID:46118,13 pages DOI:10.4236/ijaa.2014.42028
Gravitational Lensing by Spherical Lenses
Roger Hurtado, Leonardo Castañeda, Juan M. Tejeiro
Observatorio Astronómico Nacional, Universidad Nacional de Colombia, Bogotá, Colombia
Email: rahurtadom@unal.edu.co, lcastanedac@unal.edu.co, jmtejeiros@unal.edu.co
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 26 February 2014; revised 22 March 2014; accepted 29 March 2014
ABSTRACT
In this work we introduced a new proposal to study the gravitational lensing theory by spherical lenses, starting from its surface mass density 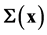 written in terms of a decreasing function
written in terms of a decreasing function 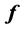 of a dimensionless coordinate
of a dimensionless coordinate 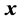 on the lens plane. The main result is the use of the function
on the lens plane. The main result is the use of the function  to find directly the lens properties, at the same time that the lens problem is described by a first order differential equation which encodes all information about the lens. SIS and NIS profiles are used as examples to find their functions
to find directly the lens properties, at the same time that the lens problem is described by a first order differential equation which encodes all information about the lens. SIS and NIS profiles are used as examples to find their functions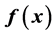 . Using the Poisson equation we find that the deflection angle is directly proportional to
. Using the Poisson equation we find that the deflection angle is directly proportional to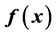 , and therefore the lens equation can be written in terms of the function and the parameters of the lens. The critical and caustic curves, as well as image formation and magnification generated by the lens are analyzed. As an example of this method, the properties of a lens modeled by a NFW profile are determined. Although the puntual mass is spherically symmetric, its mass density is not continuous so that its
, and therefore the lens equation can be written in terms of the function and the parameters of the lens. The critical and caustic curves, as well as image formation and magnification generated by the lens are analyzed. As an example of this method, the properties of a lens modeled by a NFW profile are determined. Although the puntual mass is spherically symmetric, its mass density is not continuous so that its 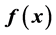 function is discussed in Appendix 1.
function is discussed in Appendix 1.
Keywords:Gravitational Lensing, Strong, Dark Matter

1. Introduction
Gravitational lensing is one of the greatest achievements of General Relativity and is one of the most useful tools of galactic astronomy, not only because the distortion of background sources carries information from the mass distribution deflecting light (called lens), but also it provides a direct test of cosmological theories [1] -[4] .
The deflection angle of the light, as well as the image multiplicities [5] and its magnifications, depends on the properties of the lens. In fact, the position and shape of the source, and the matter distribution of the lens are unknown, so you can try to resolve the problem inverting positions and shapes of the images, for expample by the Kaiser & Squires method [6] ; or you can model the lens using known mass profiles, e.g. isolated mass (PM), non-singular isothermal sphere (NIS), non-singular isothermal ellipsoid (NIE), etc., depending on parameters to be adjusted so that the model reproduces the observed data [7] [8] ; the basis of these parametric methods relies on theoretical assumptions, which encourages us to study the properties of one of the most important families of mass models: the spherical mass distribution. Due to the symmetry of these profiles, the relation between the properties of the lens-source system and its observables is reduced to a one-dimensional equation, which provides some important results from a general point of view of the theory, including image position, distortion and magnification.
Of course, due to the intrinsic ellipticity of a cluster or a galaxy, it is not physically possible to model such systems using a spherical profile. However, computer simulations suggest that the dark matter halo present in these systems can be described by a spherical mass distribution1 [9] , and in this sense, we shall describe our method to the NFW profile.
For a basic and comprehensive reference on gravitational lensing see [1] [10] [11] .
2. Convergence and Lens Equation
Suppose a spherically symmetric mass profile lying at a distance2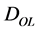 , acting as a gravitational lens on the light emitted by a source at a distance
, acting as a gravitational lens on the light emitted by a source at a distance  from us, and assume that the distance between lens and source is
from us, and assume that the distance between lens and source is . The mass projection on the lens plane, called surface mass density, is obtained through
. The mass projection on the lens plane, called surface mass density, is obtained through
 (1.1)
(1.1)
where 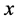 is a dimensionless radius vector on the lens plane and the coordinate
is a dimensionless radius vector on the lens plane and the coordinate 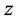 is perpendicular to it, that is to say, it is the line of sight coordinate. In this paper we suppose that
is perpendicular to it, that is to say, it is the line of sight coordinate. In this paper we suppose that
 (1.2)
(1.2)
where 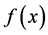 and
and  are monotonically decreasing functions because the surface mass density must describe a realistic and localized lens model, and that functions are depending on the mass distribution of the lens, and defined on the interval
are monotonically decreasing functions because the surface mass density must describe a realistic and localized lens model, and that functions are depending on the mass distribution of the lens, and defined on the interval . Worth noting that
. Worth noting that , or
, or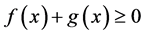 , and this can be accomplished by assuming
, and this can be accomplished by assuming  and
and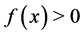 . Since
. Since  may be divergent at origin, we impose the condition
may be divergent at origin, we impose the condition
 (1.3)
(1.3)
with this, the convergence is defined by
 (1.4)
(1.4)
where 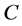 depends on both, the distances which are functions of the cosmological model, and the physical parameters of the lens mass distribution
depends on both, the distances which are functions of the cosmological model, and the physical parameters of the lens mass distribution
 (1.5)
(1.5)
Moreover, the Poisson equation relates the convergence and the deflection potential of the lens 
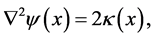 (1.6)
(1.6)
which, for a spherically symmetric mass distribution can be expressed as
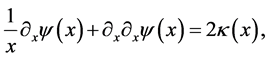 (1.7)
(1.7)
where 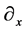 denotes the derivative with respect to
denotes the derivative with respect to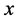 . The Poisson equation leads to the deflection angle from
. The Poisson equation leads to the deflection angle from
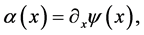 (1.8)
(1.8)
thus, from Equation (1.7) can be found that
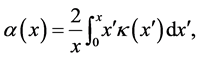 (1.9)
(1.9)
or, by Equation (1.4)
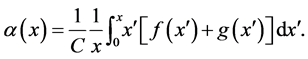 (1.10)
(1.10)
Now, since 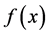 is a decreasing function
is a decreasing function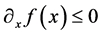 , and since
, and since 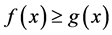 we write the
we write the 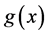 function from
function from 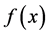 to which an amount
to which an amount 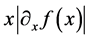 is subtracted, that is
is subtracted, that is
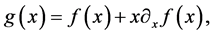 (1.11)
(1.11)
this assumption is made in order to use the fundamental theorem of calculus in the integral expression of the deflection angle, Equation (1.10), so that
 (1.12)
(1.12)
that is
 (1.13)
(1.13)
The anterior result shows that for a spherically symmetric mass profile, whose surface mass density can be written in the form of Equation (1.2), the deflection angle is proportional to the function .
.
The lens equation, which relates the image and source positions,  and
and  respectively, for a spherically symmetric situation, is a scalar and takes the one dimensional form,
respectively, for a spherically symmetric situation, is a scalar and takes the one dimensional form,
 (1.14)
(1.14)
which can be written in terms of the  function as
function as
 (1.15)
(1.15)
Joining the results given above, the 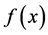 function satisfies the following equation
function satisfies the following equation
 (1.16)
(1.16)
which comes from inserting Equation (1.11) in Equation (1.4), according to the initial condition (1.3). Thus, the problem is reduced to solve the first-order ordinary differential Equation (1.16) for .
.
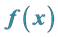 for SIS and NIS Profiles
for SIS and NIS Profiles
A spherical model widely used in the gravitational lensing theory is the singular isothermal sphere (SIS) [10] , whose convergence is given by
 (1.17)
(1.17)
where  is the one-dimensional velocity dispersion. With Equation (1.17) plugged into Equation (1.16) and Equation (1.3), one obtains the
is the one-dimensional velocity dispersion. With Equation (1.17) plugged into Equation (1.16) and Equation (1.3), one obtains the 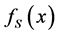 function for a SIS
function for a SIS
 (1.18)
(1.18)
 (1.19)
(1.19)
with
 (1.20)
(1.20)
The 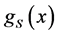 function is then for a SIS
function is then for a SIS
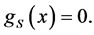 (1.21)
(1.21)
To find the deflection angle, make the product  with
with 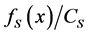
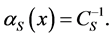 (1.22)
(1.22)
One generalization of the SIS model is frequently used with a finite core , that is the non-singular isothermal sphere (NIS), which is more realistic for modeling galaxies. In this case, the convergence is given by
, that is the non-singular isothermal sphere (NIS), which is more realistic for modeling galaxies. In this case, the convergence is given by
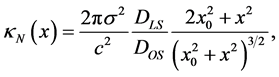 (1.23)
(1.23)
Through a procces similar to the SIS, we can found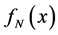 ,
,  and
and  for the NIS profile
for the NIS profile
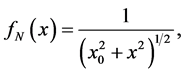 (1.24)
(1.24)
 (1.25)
(1.25)
and
 (1.26)
(1.26)
where  is given by Equation (1.20).
is given by Equation (1.20).
3. Magnification and Shear
Since gravitational lensing conserves the surface brightness, the magnification of an image is defined as the ratio between the solid angles of the image and the source. Namely
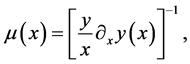 (1.27)
(1.27)
from Equation (1.11) and Equation (1.15), this is
 (1.28)
(1.28)
Equation (1.28) implies that the magnification has two singularities in  and
and  and therefore its curve has two asymptotes at these points. In the next section we will see that those points in the lens plane for
and therefore its curve has two asymptotes at these points. In the next section we will see that those points in the lens plane for  and
and  are the critical points.
are the critical points.
Noting that the magnification Equation (1.28) can be written in terms of the convergence  and shear
and shear , which measures the distortion of images,
, which measures the distortion of images,
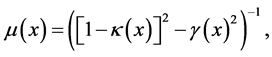 (1.29)
(1.29)
whereby
 (1.30)
(1.30)
and from Equation (1.4), the shear is
 (1.31)
(1.31)
This expression allows to calculate 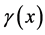 in a straightforward way. For example, returning to the models shown in
in a straightforward way. For example, returning to the models shown in  1.2.1, through Equation (1.19) and Equation (1.21), the shear generated by a SIS profile is
1.2.1, through Equation (1.19) and Equation (1.21), the shear generated by a SIS profile is
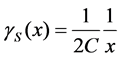 (1.32)
(1.32)
and that generated by a NIS profile
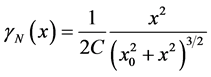 (1.33)
(1.33)
where we made use of Equation (1.24) and Equation (1.25).
Now, recognizing that
 (1.34)
(1.34)
and
 (1.35)
(1.35)
the shear can be written in terms of the deflection potential of a mass distribution with spherical symmetry, as
 (1.36)
(1.36)
Here, the definition of the 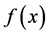 function shows again its usefulness, since the shear can be found in terms of the deflection potential without have recourse to the partial derivatives of it.
function shows again its usefulness, since the shear can be found in terms of the deflection potential without have recourse to the partial derivatives of it.
4. Critical and Caustics Curves
The critical curves are those points  in the lens plane where the lens equation can not be inverted, or equivalently, those points where the magnification is infinite, which satisfy
in the lens plane where the lens equation can not be inverted, or equivalently, those points where the magnification is infinite, which satisfy
 (1.37)
(1.37)
or
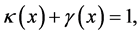 (1.38)
(1.38)
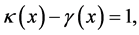 (1.39)
(1.39)
but, from Equation (1.4) and Equation (1.31)
 (1.40)
(1.40)
and
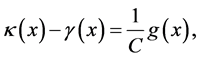 (1.41)
(1.41)
Thus, the critical curves are the level contours of the 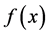 and
and  functions, and are found when
functions, and are found when
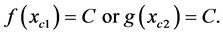 (1.42)
(1.42)
Equation (1.42) are not associated forming a system, thus, given  it is possible found two solutions
it is possible found two solutions 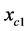 and
and  if
if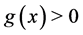 , or
, or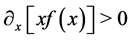 , meaning that
, meaning that  is increasing, and, if
is increasing, and, if , so that
, so that 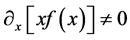 and therefore if
and therefore if , with
, with  and
and  two arbitrary constants. In this way, the only condition for forming two critital circles is that
two arbitrary constants. In this way, the only condition for forming two critital circles is that 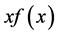 is incresing, otherwise the lens produces only a single critical curve associated to
is incresing, otherwise the lens produces only a single critical curve associated to , or any critical curve if
, or any critical curve if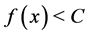 . At the same time, the caustics curves are the corresponding locations in the source plane of the critical curves through the lens equation, and if we assume that the lens produces two critical curves, that is,
. At the same time, the caustics curves are the corresponding locations in the source plane of the critical curves through the lens equation, and if we assume that the lens produces two critical curves, that is,
 (1.43)
(1.43)
 (1.44)
(1.44)
with 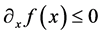 on
on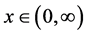 . Thus, caustic curves will be a point and a circle concentric with the lens.
. Thus, caustic curves will be a point and a circle concentric with the lens.
5. Image Formation
In general, the image multiplicity depends on the source position with respect to the caustic circle, changing in two as the source crosses through it. Moreover caustics depends on the critical curves and on the increase or decrease of  as seen in the previous section. Figure 1 shows the two basic sketches for the function
as seen in the previous section. Figure 1 shows the two basic sketches for the function 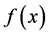 for the two lens models mentioned in Section
for the two lens models mentioned in Section  2.1: the SIS and the NIS profiles, where we can see that although
2.1: the SIS and the NIS profiles, where we can see that although 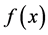 is decreasing, the product
is decreasing, the product 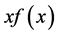 can be increased or constant, but this depends on the lens model as follows:
can be increased or constant, but this depends on the lens model as follows:
• If 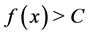 in
in 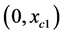 and
and 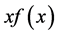 is increasing,
is increasing,  does exist and the maximum number of images are three.
does exist and the maximum number of images are three.
• If 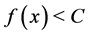 in
in 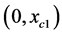 and
and 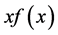 is decreasing,
is decreasing, 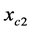 does not exist and the total number of images are two.
does not exist and the total number of images are two.
• If  for
for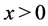 , then
, then 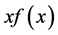 is increasing and there is only one image.
is increasing and there is only one image.
In the case where the lens produces three images the source is inside the caustic circle, that is 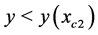 and let us call those images,
and let us call those images,  ,
, 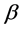 and
and , which together obey
, which together obey
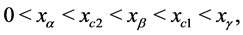 (1.45)
(1.45)
or
 (1.46)
(1.46)
with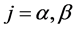 ; and since
; and since  is decreasing in
is decreasing in ,
,
 (1.47)
(1.47)
Now suppose the source located in the first quadrant of a cartesian coordinate system in whose center lies the lens; namely  with
with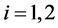 . The lens mapping (1.15), is, by components
. The lens mapping (1.15), is, by components

Figure 1. Function f(x) for two lens models, the singular isothermal sphere and the Non-singular isothermal sphere (NIS). In the case of SIS xf(x) is constant, while f(x) is decreasing. In the NIS model xf(x) is increased, unlike f(x).
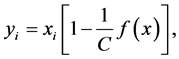 (1.48)
(1.48)
through Equation (1.47)
 (1.49)
(1.49)
This implies
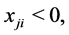 (1.50)
(1.50)
therefore, the images 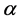 and
and  will be in the third quadrant. And since the angle of
will be in the third quadrant. And since the angle of  is,
is,
 (1.51)
(1.51)
the angle of images will be
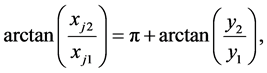 (1.52)
(1.52)
that is, the images  and
and 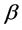 lies on the same line connecting the source and lens, but are diametrically opposed to the latter one.
lies on the same line connecting the source and lens, but are diametrically opposed to the latter one.
Meanwhile, the third image 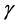 satisfies
satisfies , as
, as
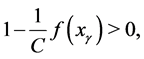 (1.53)
(1.53)
and since , it is found
, it is found , with
, with . This implies that the angle of
. This implies that the angle of 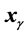 is equal to that of the source. The third image also lies in the same line between lens and source.
is equal to that of the source. The third image also lies in the same line between lens and source.
If the lens produces only two images, they are diametrically opposed lying on the line lens-source. And, if the lens produces only one image, it will be located at the same angle of the source.
6. Applying Theory to the NFW Profile
The lensing effects of the NFW profile have been widely studied [12] -[14] . The NFW profile describes the distribution of a dark matter halo. The dark matter halo is useful to calculate the function 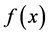 in this model.
in this model.
Suppose a gravitational lens modeled by a NFW profile [9] with a mass density given by
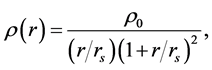 (1.54)
(1.54)
where the so called scale radius 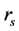 and
and  are parameters of the halo.
are parameters of the halo.
6.1. NFW Convergence and Lens Equation
The NFW mass density Equation (1.54) expressed in terms of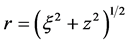 , where
, where  is a radius vector on the lens plane, and Equation (1.1) leads to the convergence through
is a radius vector on the lens plane, and Equation (1.1) leads to the convergence through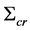 , Equation (1.5), to obtain
, Equation (1.5), to obtain
 (1.55)
(1.55)
this expression is according with the results found in [15] and [12] . Here we have defined 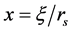 and
and
 (1.56)
(1.56)
Equation (1.16) and Equation (1.55) leads to the differential equation
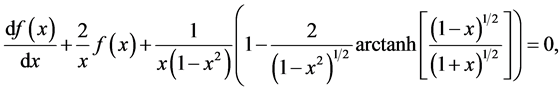 (1.57)
(1.57)
finding that
 (1.58)
(1.58)
where we use Equation (1.3). Therefore
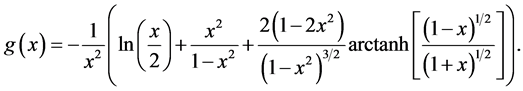 (1.59)
(1.59)
Figure 2 shows the functions 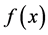 and
and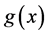 , which, as they should be, are decreasing in
, which, as they should be, are decreasing in  for
for  and
and .
.
The deviation angle can be calculated through Equation (1.13)
 (1.60)
(1.60)
where the 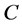 constant is given by Equation (1.56). Now, it is straightforward that the lens equation for a mass distribution modelled by the NFW profile, reads as
constant is given by Equation (1.56). Now, it is straightforward that the lens equation for a mass distribution modelled by the NFW profile, reads as
 (1.61)
(1.61)
The behavior of the lens equation is shown in Figure 3. There it can be seen that the local maxima and minima of the lens equation depends on the parameters of the model, these points correspond to critical curves.
Figure 4 shows the lens equation in the case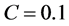 . Depending on the source position there are four posibilities of image formation, if:
. Depending on the source position there are four posibilities of image formation, if:
• 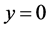 , there are infinite images (Einstein’s ring of radius
, there are infinite images (Einstein’s ring of radius ), if
), if
• 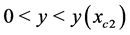 , there are three images, the first within the circle of radius
, there are three images, the first within the circle of radius  and second one outside of it, but within of that of radius
and second one outside of it, but within of that of radius , and third outside the circle of radius
, and third outside the circle of radius , but within that of radius
, but within that of radius , if
, if
•  , there are two images in
, there are two images in  and
and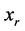 , and if
, and if
• 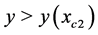 , there is only one image outside of the circle of radius
, there is only one image outside of the circle of radius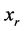 .
.
6.2. NFW Critical and Caustics Curves
In Figure 5 are displayed the local maxima of the lens equation as a function of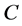 . This values are the inverse functions
. This values are the inverse functions  and
and 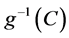 and therefore, they correspond to the radii of the critical circles, in fact, their maximum values are taken when
and therefore, they correspond to the radii of the critical circles, in fact, their maximum values are taken when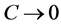 , where,
, where, 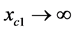 and
and . The radius of the caustic circle, also as a function of
. The radius of the caustic circle, also as a function of , is shown in the same plot.
, is shown in the same plot.
6.3. NFW Shear, Image Positions and Magnification
From Equation (1.31), we find
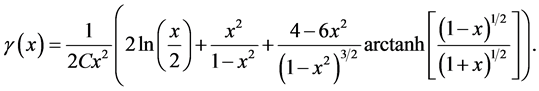 (1.62)
(1.62)
Shear Equation (1.62) is a continuous and decreasing function over the range , as it must be since shear is a lensing effect that should be diminish as the distance to the lens increases. In fact
, as it must be since shear is a lensing effect that should be diminish as the distance to the lens increases. In fact
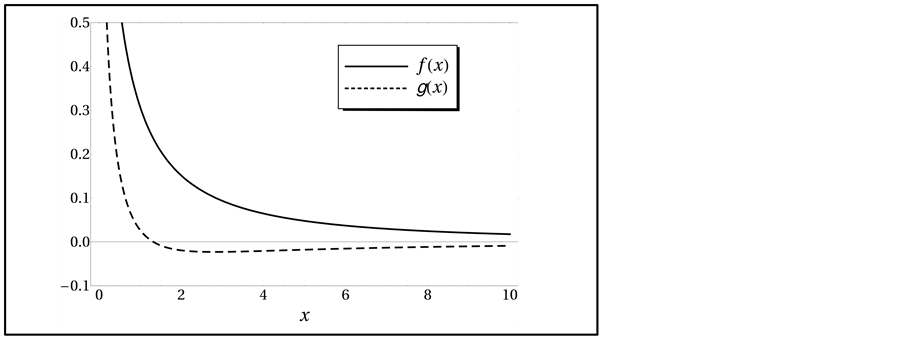
Figure 2. An horizontal line,  , determines the critical curves when crossed with the functions
, determines the critical curves when crossed with the functions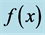 , Equation (1.58), and
, Equation (1.58), and , Equation (1.59). Note that in
, Equation (1.59). Note that in 
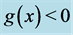 .
.
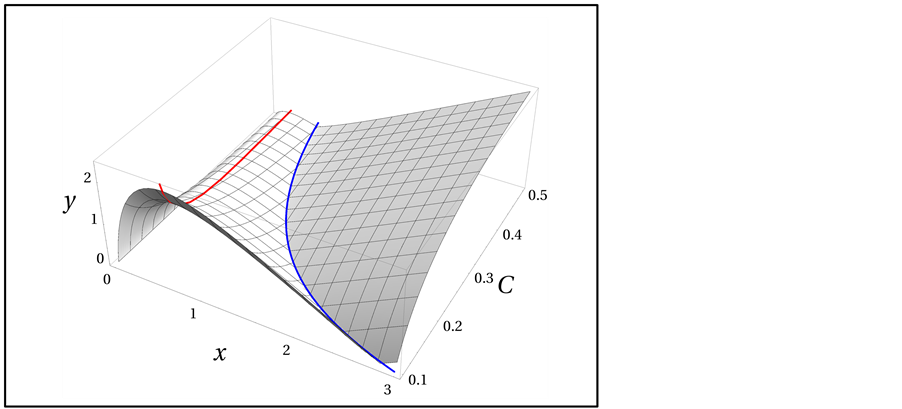
Figure 3. Lens equation by a NFW model, Equation (1.61). As shown, the image positions will depend on the magnitud of the source and the parameters of the profile, rs, ρc and δk, represented by C, Equation (1.56). The local maxima and minima (red and blue lines), corresponds to the radius of the critical circles.
 (1.63)
(1.63)
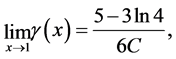 (1.64)
(1.64)
and
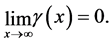 (1.65)
(1.65)
Figure 6 shows position of the images for different values of the source position. The change in position of the images is smaller as  increases and
increases and  decreases. The greater
decreases. The greater , and the lower source position, the position of the
, and the lower source position, the position of the 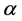 image tends to zero, the
image tends to zero, the  image tends to the inner critical circle and the
image tends to the inner critical circle and the  image tends
image tends

Figure 4. Lens equation by a NFW model for C = 0.1. In xc1 ≠ 0, the function intercepts the horizontal axis and takes its minimum value. In xc2 the function takes its local maximum in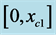 . If
. If 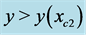 the images will be located outside the circle of radius xr.
the images will be located outside the circle of radius xr.

Figure 5. Behavior of the points xc1 and xc2 where the lens equation takes its maximum values. Radius of the caustic circle associated to xc2, as a function of C. This curves were found numerically.
to the outer critical circle.
At the same time, the magnification, given by Equation (1.28) though Equation (1.58) and Equation (59) is plotted in Figure 7 for two values 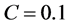 and
and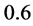 . There, we can see that the
. There, we can see that the  image is highly demagnified when it approaches to zero, and the same occurs to the
image is highly demagnified when it approaches to zero, and the same occurs to the 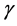 image when
image when 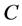 increases.
increases.
7. Conclusions
In this paper we introduce a new proposal to study the gravitational lens effect by a spherically symmetric mass distribution. The main result is the use of a new function 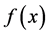 which depends on the lens properties and the lens problem is described by the first order differential Equation (1.16) which encodes all information about lensing observables. If the surface mass density of the lens is continuous, this method leads to the deflection angle in a direct way by multiplying the function for the dimmensionless coordinate
which depends on the lens properties and the lens problem is described by the first order differential Equation (1.16) which encodes all information about lensing observables. If the surface mass density of the lens is continuous, this method leads to the deflection angle in a direct way by multiplying the function for the dimmensionless coordinate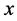 . We describe the critical and caustic curves through an equation that relates the function and the parameter
. We describe the critical and caustic curves through an equation that relates the function and the parameter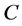 , Equation (1.56), of the
, Equation (1.56), of the

Figure 6. Image positions of a point source as a function of C. The critical curves xc1 (blue) and xc2 (red) divides the source plane in three regions of image formation, that is, depending of the source position we can found up to 3 images. In agreement to Section (1.5), solid black lines represents the position of the first image (α), dotted lines, the second one (β), and the dashed lines, the third (γ), for each case of . The three images are associated as follows: each of the curves from left to right and under xc1 is associated with one curve from top to bottom above xc1. If the image position approaches to zero, i.e.
. The three images are associated as follows: each of the curves from left to right and under xc1 is associated with one curve from top to bottom above xc1. If the image position approaches to zero, i.e. , then the Einstein Ring of radius xc1 is formed, and the images
, then the Einstein Ring of radius xc1 is formed, and the images 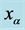 and
and  go to zero, as we can see from the plot.
go to zero, as we can see from the plot.
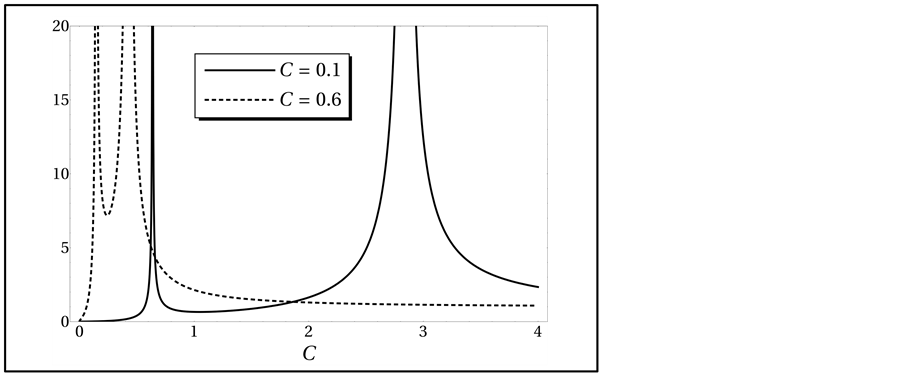
Figure 7. Magnification of images in the lens plane for two values of C. The asymptotes will form in xc1 and xc2 (in each curve from right to left, respectively). Simulation of the image formation for a circular lens, magnification, critical and caustic curves generated by a lens modeled through a NFW profile is available online.
lens which contains all the physical information of the lens and also is a function of the cosmological model.
The importance of the method described in this paper is that if you resolve Equation (1.16) for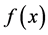 , then you can find the lens observables directly in terms of that function. This implies that you do not need to solve the Poisson equation to find the deflection potential, and this is an advantage.
, then you can find the lens observables directly in terms of that function. This implies that you do not need to solve the Poisson equation to find the deflection potential, and this is an advantage.
In the case where the convergence is not a continuous function of the space, the differential Equation (1.16) can still be used to find the 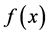 function, however, the deflection angle must be calculated through Equation (1.10). In Appendix 1 we explore this approach by the point mass lens.
function, however, the deflection angle must be calculated through Equation (1.10). In Appendix 1 we explore this approach by the point mass lens.
We apply the method to a lens modelled by the NFW profile and found explicitly the function 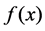 in this case. The critical and caustic curves, shear, magnification and the image formation are found for this model using the formalism proposed in the first part of this paper.
in this case. The critical and caustic curves, shear, magnification and the image formation are found for this model using the formalism proposed in the first part of this paper.
Acknowledgements
R. Hurtado is grateful with Y. Villota for some helpful suggestions that improved the presentation of the paper and the Universidad Nacional de Colombia for financial support.
References
- Blandford, R.D. and Narayan, R. (1992) Cosmological Applications of Gravitational Lensing. ARA&A, 30, 311-358. http://dx.doi.org/10.1146/annurev.aa.30.090192.001523
- Yu-Chung, N. and Cheng, L. (1999) Krauss, Gravitational Lensing and Dark Structures. The Astrophysical Journal, 514, 25-32. http://dx.doi.org/10.1086/306914
- Brouzakis, N., Tetradis, N. and Tzavara, E. (2008) Light Propagation and Large-Scale Inhomogeneities. Journal of Cosmology and Astroparticle Physics, 4, 8.
- Shuo, C., Yu, P., Biesiada, M., Godlowski, W. and Zong-Hong, Z. (2012) Constraints on Cosmological Models from Strong Gravitational Lensing Systems. Journal of Cosmology and Astroparticle Physics, 3, 16.
- Cohn, J.D. and Kochanek, C.S. (2014) The Effects of Massive Substructures on Image Multiplicities in Gravitational Lenses. The Astrophysical Journal, 608, 25-35. http://dx.doi.org/10.1086/392491
- Kaiser, N. and Squires, G. (1993) Mapping the Dark Matter with Weak Gravitational Lensing. The Astrophysical Journal, 404, 441-450. http://dx.doi.org/10.1086/172297
- Knudson, A., Ratnatunga, K.U. and Griffiths, R.E. (2001) Investigation of Gravitational Lens Mass Models. The Astronomical Journal, 122, 103-112.
- Halkola, A., Seitz, S. and Pannella, M. (2006) Parametric Strong Gravitational Lensing Analysis of Abell 1689. Monthly Notices of the Royal Astronomical Society, 372, 1425-1462. http://dx.doi.org/10.1111/j.1365-2966.2006.10948.x
- Navarro, J., Frenk, C. and White, S. (1996) The Structure of Cold Dark Matter Halos. The Astrophysical Journal, 462, 563-575. http://dx.doi.org/10.1086/177173
- Schneider, P., Ehlers, J. and Falco, E.E. (1992) Gravitational Lenses. Springer-Verlag, Berlin.
- Wambsganss, J. (1998) Gravitational Lensing in Astronomy. Living Reviews in Relativity, 1, 12. http://www.livingreviews.org/lrr-1998-12
- Wright, C.O. and Brainerd, T.G. (2000) Gravitational Lensing by NFW Halos. The Astrophysical Journal, 534, 34-40. http://dx.doi.org/10.1086/308744
- Golse, G. and Kneib, J.P. (2002) Pseudo Elliptical Lensing Mass Model: Application to the NFW Mass Distribution. Astronomy & Astrophysics, 390, 821-827.
- Narikawa, T. and Yamamoto, K. (2012) Testing Gravity with Halo Density Profiles Observed through Gravitational Lensing. Journal of Cosmology and Astroparticle Physics, 5, 16.
- Bartelmann, M. (1996) Arcs from a Universal Dark-Matter Halo Profile. The Astronomical Journal, 313, 697-702.
Appendix 1. Point Mass
Supposse a point lens at the origin of a reference frame, whose convergence, given in terms of the Dirac Delta function , is
, is
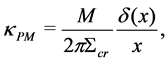 (1.66)
(1.66)
with Equation (1.16) we can obtain the differential equation
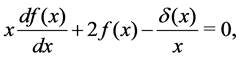 (1.67)
(1.67)
where we take
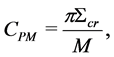 (1.68)
(1.68)
the solution for Equation (1.67) is
 (1.69)
(1.69)
where 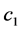 is the constant relate to the initial condition of the equation and
is the constant relate to the initial condition of the equation and 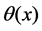 is the Heaviside function. Now, through Equation (1.11), we can obtain
is the Heaviside function. Now, through Equation (1.11), we can obtain
 (1.70)
(1.70)
It is worth highlighting that the surface mass density of the point mass lens is not a continuos function, in fact, the Dirac Delta is a distribution, therefore, the 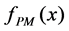 and
and  functions only will have meaning when we integrate them. For this, the deflection angle can not be calculated through Equation (1.13), instead of this, we must use Equation (1.10)
functions only will have meaning when we integrate them. For this, the deflection angle can not be calculated through Equation (1.13), instead of this, we must use Equation (1.10)
 (1.71)
(1.71)
where we can appreciate that the 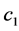 constant of the differential equation is irrelevant to the solution of the problem. So
constant of the differential equation is irrelevant to the solution of the problem. So
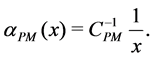 (1.72)
(1.72)
This is the deflection angle found frequently in the literature which can be found from General Relativity.
NOTES

1This profile is the result of the N-body simulations of collapsed structures called halos.
2All distances mentioned in this paper are angular diameter distances.

3That is, lower central density of the lens Equation (1.56).

