International Journal of Astronomy and Astrophysics
Vol. 3 No. 2A (2013) , Article ID: 33025 , 4 pages DOI:10.4236/ijaa.2013.32A003
Calculation of 10Be & 14C Production Rates in the Solar Atmosphere: Implications for Solar Flare Spectral Index
Department of Physics, Purdue University North Central, Westville, USA
Email: gbricker@pnc.edu
Copyright © 2013 Glynn E. Bricker. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 18, 2013; revised February 20, 2013; accepted February 28, 2013
Keywords: Solar Wind; Radio-Nuclide; 10Be; 14C; Solar Flare Parameter
ABSTRACT
Production rates for the short-lived radionuclides 10Be (T1/2=1.36Myr) and 14C (T1/2=5730 yr) in the solar atmosphere were calculated. As both radionuclides are produced through spallation reaction of solar energetic particles (SEP) with oxygen as the primary target, the prevalence of each radionuclide is linked. For the calculations, we assumed power law distribution for SEP with spectral index, r, ranging from 2.5 to 4. We find the 10Be and 14C flux rate at the surface of the Sun to range from 0.007 cm−2∙s−1 to 2.55 cm−2∙s−1 for 10Be, and from 0.13 cm−2∙s−1 to 24.13 cm−2∙s−1 for 14C. These radio-nuclides are then entrained in the solar wind. From these flux rate calculations and comparison with experimentally measured flux rates, we find the most likely time averaged solar flare spectral index to be r = ~3.3.
1. Introduction
Particles that bombard the Earth’s atmosphere originating from outside the Earth, broadly called here cosmic rays, come in three varieties: solar wind ions, SEP, and GCRs (galactic cosmic rays), differentiated primaries by their kinetic energies. Specific information about the cosmic ray type is given in Table 1.
Preliminary observations of solar wind ions began with the early space mission Lunik 2, Lunik 3, Venus probe, and Explorer 10; results from the Mariner 2 mission unequivocally demonstrated the existence of a continuous solar wind (e.g. [1]). Solar wind ions typically have energy of a few keV, so they typically do not participate in the production of cosmogenic nuclides. Solar wind ions can be implanted on the surface of extraterrestrial materials as they can penetrate to a depth of several hundred angstroms.
Direct evidence for the occurrence of solar wind im
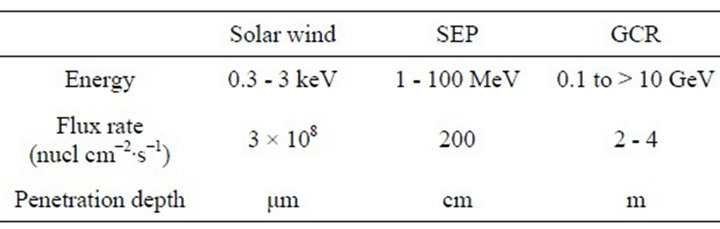
Table 1. Cosmic Ray Parameters.
planted ions in extraterrestrial materials comes from lunar samples. Nishiizumi and Caffee [2] detected solarwind-implanted 10Be in Apollo 17 trench samples, and Jull et al. [3,4] measured solar-wind-implanted 14C in Apollo 11, 16, and 17 soil samples. Lunar samples also contain surface implanted solar wind noble gases, including Ne and Ar [5].
Lange and Forbush [6] were the first to detail solar flares after two exceptionally large flaring events in spring of 1942. Observations indicate that flaring can occur at any time, but flaring events are more likely and more energetic around solar maximums. Energy of the accelerated particles ranges from a few MeV/nucl up to several hundred MeV/nucl, with most of the particles having lower energy. The differential particle flux of energetic particles from the Sun behaves as a power law in kinetic energy E:
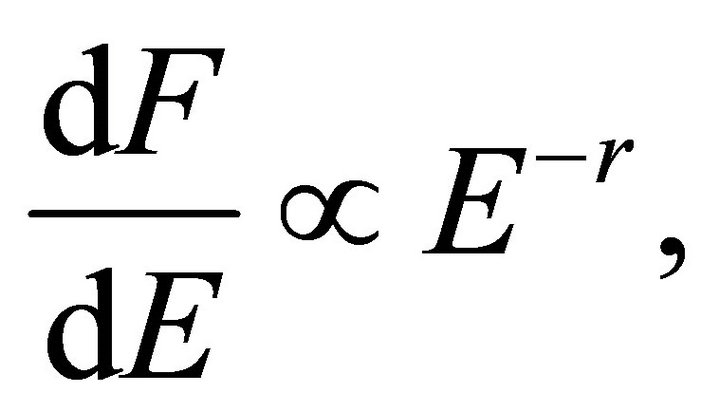 (1)
(1)
where  is the differential particle flux at Energy E, and r is the spectral index describing the flare; r typically ranges from 2.5 to 4.
is the differential particle flux at Energy E, and r is the spectral index describing the flare; r typically ranges from 2.5 to 4.
Solar flares release large amounts of energy, and produce many energetic particles, including protons and various ions [7]. These SEP can interact with ambient gaseous target material in the solar atmosphere, producing daughter nuclei through nuclear reactions. Measurements of gamma-ray emission indicate nuclear interactions do occur at various depths in the solar atmosphere [8]. The radionuclides 10Be and 14C are examples of daughter nuclei which can be produced through spallation reactions with energetic particles originating in solar flares [9]. The main targets for 10Be production are C and O, although O is the primary target, and the main target for 14C production is also O. A portion of this spallogenic 10Be and 14C escapes the Sun and becomes entrained in the solar wind. Eventually some fraction of the solar wind radionuclides intersects the Moon, and becomes implanted on the lunar surface. As the solar wind ions typically have energies of about 1 keV/nucl, they are therefore implanted on the very surface, to a depth of up to ~30 nm [4]. Nishiizumi and Caffee [2] measured the surface correlated, i.e. solar wind 10Be, in Apollo 17 lunar trench sample 78481, and find the 10Be implantation rate to be ~2.5 × 10−6 cm−2∙s−1 at the surface of the Moon. This corresponds to an escape rate of 10Be from the Sun of 0.1 cm−2∙s−1. Jull et al. [3,4] measured the solar wind implanted 14C in Apollo 11, 16, and 17 lunar soil samples, and from this data we find flux rate to be ~2 - 20 14C cm−2∙s−1 at the surface of the Sun. In this paper, we calculate the production rates for both 10Be and 14C in the solar atmosphere from SEP for a range of solar flare spectral indices. From these calculations, and comparison with experimentally determined solar-wind-implantation rates for each radionuclide at the lunar surface, we calculate the most likely time averaged solar flare spectral index.
2. Cosmogenic Nuclide Production
Nuclear spallation reactions occur when an incident energetic particle interacts with the nucleus of another atom, producing a cascade of secondary particles. For the reaction to occur, the incident particle must overcome the nuclear binding energy of the target atom. The lower energy secondary particles are free to induce lower energy spallation reactions of their own. Spallation reactions typically occur >10 MeV, but the threshold is dependent upon the type of incident particle and energy of the particle and the elemental composition of the target. Nuclear spallation reactions are typically of the type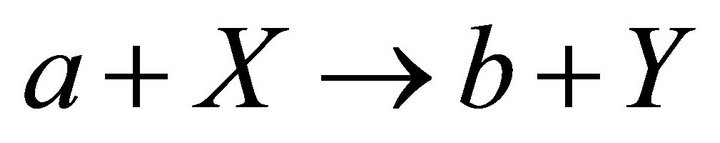 , were a is the incident particle, X is the target, b is the secondary reaction product, and Y is the reaction product. Shorthand notation for this reaction is
, were a is the incident particle, X is the target, b is the secondary reaction product, and Y is the reaction product. Shorthand notation for this reaction is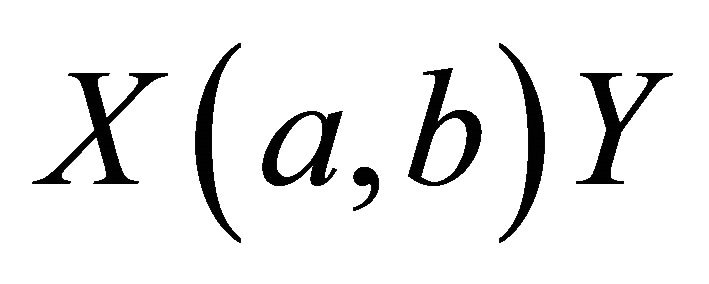 .
.
2.1. SEP Characteristics
We calculate the SLR production rates assuming the protons are characterized by a power law relationship:
 (2)
(2)
where r ranges from 2.5 to 4. From Reedy [10] we assume an integrated energetic proton flux of ~200 protons cm−2∙s−1 for E > 10 MeV at 1 AU. This corresponds to 9.3 × 106 protons cm−2∙s−1 at the surface of the Sun.
2.2. Production Rate Calculation
The production rates for cosmogenic nuclides can be calculated via:
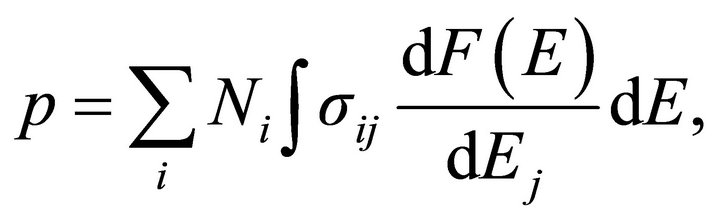 (3)
(3)
were i represents the target elements for the production of the considered nuclide, 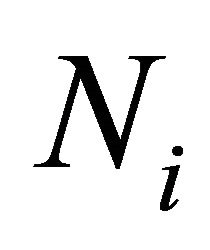 is the abundance of the target element (g∙g−1), j indicates the energetic particles that cause the reaction,
is the abundance of the target element (g∙g−1), j indicates the energetic particles that cause the reaction,  is the cross section for the production of the nuclide from the interaction of particle j with energy E from target i for the considered reaction (cm2), and
is the cross section for the production of the nuclide from the interaction of particle j with energy E from target i for the considered reaction (cm2), and  is the differential energetic particle flux of particle j at energy E (cm−2∙s−1) [7]. We assume gaseous targets of solar composition from Lodders [11], where the density of the photosphere is ~1 × 10−7 g∙cm−3 [12].
is the differential energetic particle flux of particle j at energy E (cm−2∙s−1) [7]. We assume gaseous targets of solar composition from Lodders [11], where the density of the photosphere is ~1 × 10−7 g∙cm−3 [12].
2.3. Nuclear Cross-Sections
To calculate the production rate of 10Be, we use the cross-sections from Gounelle et al. [13]. These are a combination of experimental data and model simulations from Sisterson et al. [14], Iljinov et al. [15], and Lange et al. [16]. For 14C, we use the cross sections from Sisterson et al. [17], which are a compilation of experimental data.
We estimate the uncertainty associated with the cross sections to be roughly a factor of two. The reactions considered here are the main nuclear production pathways, taking into account both the abundance of the target material and the cross-section. Reactions not considered would most likely add little to the overall production rates.
3. Results
We use Equation (3) to calculate the production rates for both 10Be and 14C from SEP in the solar atmosphere. We use the integrated SEP flux of 9.3 × 106 protons cm−2∙s−1 at the surface of the Sun for E > 10 MeV [10], and assume a power law distribution as in Equation (2), where r goes from 2.5 to 4. The cross-section functions and target are abundances are given in Sections 2.2 and 2.3, respectively. The results of production rate calculations from Equation (3) for a range of spectral indices for both 10Be and 14C are given in Figure 1 below. Table 2 also shows the results from Equation (3), and includes the predicted 14C/10Be production ratio.
The production flux rate for 10Be ranges from 0.007 cm−2∙s−1 for r = 4 to 2.55 cm−2∙s−1 for r = 2.5. The production flux rate for 14C ranges from about 0.13 cm−2∙s−1 for r = 4 to 24.13 cm−2∙s−1 for r = 2.5.
4. Discussion
Nishiizumi and Caffee [2] report the 10Be flux rate at the
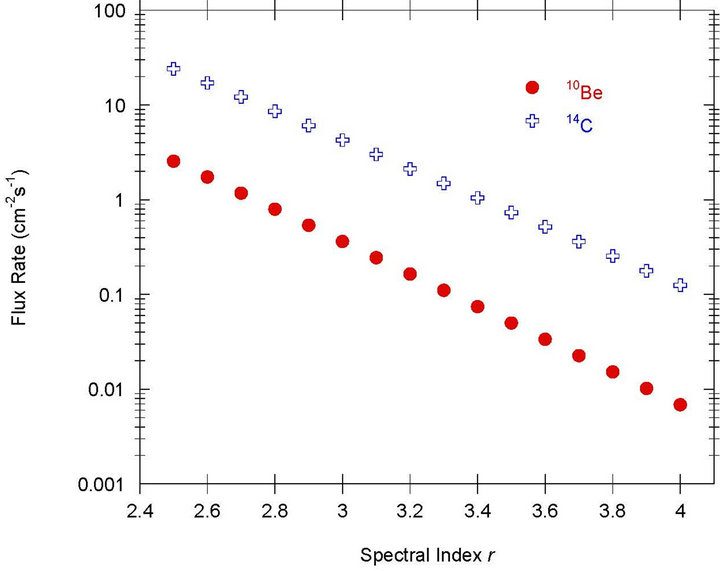
Figure 1. Production flux rate of 10Be and 14C from the spallation reaction on energetic protons on O target of solar abundance.

Table 2. 10Be and 14C flux rates, and 14C/10Be production ratios.
surface of the Sun to be 0.13 ± 0.05 cm−2∙s−1. From the results presented in the previous section, and taking into account uncertainties in the cross-sections, we find that the time averaged spectral index must range from 3.1 to 3.4 in order to reproduce the measured 10Be flux rate. The experimentally determined flux rate at the surface of the Sun for 14C ranges from ~2 to 20 cm−2∙s−1 [3,4]. Taking into account uncertainties, calculations from the previous section indicate that the spectral index must range from 2.5 to 3.5 to reproduce the wide spread in 14C measured flux rate.
The production of 10Be and 14C are connected in that the have oxygen as a common main target element. The production ratio of 14C/10Be is independent of the integrated particle flux as production rates scale linearly with incident particle flux rates. The 14C/10Be ratio is also independent of absolute elemental target abundances. The 14C/10Be ratio ranges from about 10 to 20, as depicted in Table 2. Using available 10Be [2] and 14C [3,4] data, the experimentally determined ratio for 14C/10Be at the surface of the Sun ranges from 20 to 200. It is feasible to simultaneously produce 10Be at ~0.1 cm−2∙s−1 and 14C at ~2 cm−2∙s−1, but it is not possible to simultaneously produce 10Be at ~0.1 cm−2∙s−1, and 14C at ~20 cm−2∙s−1.
Clearly, some other mechanism is needed to explain the higher 14C ratio as calculations indicate simple solar wind implantation does not yield enough 14C. One possible source is the spallation production from GCR at the lunar surface. Production of 10Be from GCR is nearly negligible, but production of 14C from GCR can occur in appreciable amounts [18]. It is possible that some of the “excess” 14C can be attributed to GCR. Although beyond the scope of this paper, those calculations are needed to elucidate the 14C contribution from sources other than the solar wind.
5. Conclusion
The production rates for both 10Be and 14C have been calculated in the solar atmosphere. The production rate we found for 10Be was consistent with experimentally determined 10Be rates with spectral index of 3.1 to 3.4. The 14C production was also found to be consistent with experimentally determined 14C rates with spectral index of 2.5 to 3.5. It is not possible to produce the measured 14C/10Be ratio with simple solar wind implantation for samples with a 14C flux rate of ~20 cm−2∙s−1, indicating that a portion of the 14C may be from GCRs. From the solar wind contribution of 10Be and 14C, we find the time averaged spectral index of the Sun to be ~3.3.
REFERENCES
- M. Neugebauer and C. W. Snyder, “The Mission of Mariner II: Preliminary Observations, Solar Plasma Experiment,” Science, Vol. 138, No. 3545, 1962, pp. 1095-1097.
- K. Nishiizumi and M. W. Caffee, “Beryllium-10 from the Sun,” Science, Vol. 294, No. 5541, 2001, pp. 352-354. doi:10.1126/science.1062545
- A. J. T Jull, D. Lal and D. J. Donahue, “Evidence for a Non-Cosmogenic Implanted 14C Component in Lunar Samples,” Earth & Planetary Science Letters, Vol. 136, No. 3-4, 1995, pp. 693-702. doi:10.1016/0012-821X(95)00163-7
- A. J. T. Jull, D. Lal, L. R. McHargue, G. S. Burr and D. J. Donahue, “Cosmogenic and Implanted Radionuclides Studied by Selective Etching of Lunar Soils,” Nuclear Instruments & Methods in Physics Research Section B, Vol. 172, No. 1-4, 2000, pp. 867-872. doi:10.1016/S0168-583X(00)00232-9
- R. O. Pepin, R. H. Becker and D. J. Schlutter, “Irradiation Records in Regolith Materials I: Isotopic Compositions of Solar Wind Neon and Argon in Single Lunar Mineral Grains,” Geochimica et Cosmochimica Acta, Vol. 63, No. 13-14, 1983, pp. 2145-2162. doi:10.1016/S0016-7037(99)00002-2
- I. Lange and S. E. Forbush, “Note on the Effect on Cosmic-Ray Intensity of the Magnetic Storm of March 1, 1942,” Terrestrial Magnetism and Atmospheric Electricity, Vol. 47, No. 2, 1942, pp. 185-186. doi:10.1029/TE047i002p00185
- R. C. Reedy and K. Marti, “Solar-Cosmic-Ray Fluxes During the Last 10 Million Years,” In: C. P. Sonnet, M. S. Giampapa and M. S. Mathews, Eds., The Sun in Time, University of Arizona Press, Tucson, 1991, pp. 260-287.
- X. M. Hua, R. Ramaty and R. E. Lingenfelter, “Deexcitation Gamma-Ray Line Emission from Solar Flare Magnetic Loops,” The Astrophysical Journal, Vol. 341, No. 1, 1989, pp. 516-532. doi:10.1086/167513
- R. C. Reedy, “Fossil Record in the Earth Moon and Meteorites,” In: R. O. Pepin, et al. Eds., The Ancient Sun, Pergamon, Oxford, 1980, pp. 365-886.
- R. C. Reedy, “Constraints on Solar System Events from Comparisons of Recent Events and Million Year Averages,” In: K. S. BalaSunramaniam, S. L. Klein and R. N. Smartt, Eds., ASP Conference Series Solar Drivers of the Interpalnetary and Terrestrial Disturbances, ASP, San Francisco, 1996, pp. 429-436.
- K. Lodders, “Solar System Abundances and Condensation Temperatures of the Elements,” The Astrophysical Journal, Vol. 591, No. 2, 2003, pp. 1220-1247. doi:10.1086/375492
- P. Rabitaille, “The Solar Photosphere: Evidence for Condensed Matter,” Progress in Physics, Vol. 2, 2006, pp. 17-20.
- M. Gounelle, F. H. Shu, H. Shang, A. E. Glassgold, K. E. Rehm and T. Lee, “The Irradiation Origin of Beryllium Radioisotopes and Other Short-lived Radionuclides,” The Astrophysical Journal, Vol. 640, No. 2, 2006, pp. 1163- 1170. doi:10.1086/500309
- J. M. Sisterson, et al., “Measurement of Proton Production Cross Sections of 10Be and 26Al from Elements Found in Lunar Rocks,” Nuclear Instruments & Methods in Physics Research Section B, Vol. 123, No. 1-4, 1997, pp. 324-329. doi:10.1016/S0168-583X(96)00409-0
- A. S. Iljinov, et al., “Production of Radionuclides at Intermediate Energies,” In: H. Schopper, Ed., LandholtBornstein. Springer-Verlag, Berlin, Heidelberg, New York, 1994.
- H. J. Lange, et al., “Production of Residual Nuclei by α-induced Reactions on C, N, O, Mg, Al and Si up to 170 MeV,” Applied Radiation and Isotopes, Vol. 46, No. 2, 1995, pp. 93-112. doi:10.1016/0969-8043(94)00124-I
- J. M. Sisterson, et al., “Revised Solar Cosmic Ray Fluxes Estimated Using Measured Depth Profiles of 14C in Lunar Rocks; The Importance of Good 14C Cross Section Determinations,” Lunar & Planetary Science, Vol. 27, 1196, pp. 1209-1210.
- K. Nishiizumi, et al., “10Be Profiles in Lunar Surface Rock 68815,” Proceeding of 11th Lunar and Planetary Science conference, Houston, 16 March 1987, pp. 79-85.

