International Journal of Astronomy and Astrophysics
Vol.3 No.1(2013), Article ID:29430,9 pages DOI:10.4236/ijaa.2013.31003
A Synthesis of Fundamental Parameters of Spiral Arms, Based on Recent Observations in the Milky Way
National Research Council Canada, National Science Infrastructure Portfolio, Victoria, Canada
Email: jacques.vallee@nrc-cnrc.gc.ca
Received December 20, 2012; revised January 22, 2013; accepted February 1, 2013
Keywords: Interstellar Matter; Milky Way; Spiral Galaxies
ABSTRACT
Recent advances in the position and shape of each spiral arm in the Milky Way (pitch angle, shape, number, inter-arm separation at the Sun) are evaluated and compared, and a statistical analysis yields an updated idealized Galactic map. Earlier tabular results were published in five blocks of 15 to 20 each, covering 1980 to 2007 [1-4]. This paper presents the latest two blocks, each between 15 and 20 entries of published spiral arm researches since 2008. Using this revised Galactic map, and a discussion on the width of the Sagittarius arm (major or minor or equal), an interpretation of orbital streamlines for the gas and magnetic fields is presented for 2 major arms and for 4 major arms in the Milky Way. Our interpretation for all the recent data favors the following: a four-arm non-circular spiral pattern for the Milky Way; the Sagittarius arm being likely an equal arm; the inter-arm separation at the Sun’s location converging near 3.0 kpc. We emphasize that these conclusions encompass all the data, and thus can vary somewhat from the results of data obtained from a single filter (only CO data, say).
1. Introduction
This paper extends a series of papers summarizing and synthesizing investigations of the spiral structure of the Milky Way Galaxy. Given our position near the sun in the disk of the Milky Way, the majority of published observational results cannot encompassing the whole galaxy, but are focussing on one part or the other—usually near the Sun. Hence most of these studies are valuable in some area, and are included here for completeness—hence one can coin the term “meta-study”. Some studies have adapted and slightly modified earlier models of spiral arms, thus making a version that better fit their own data—here one talk of “model evolution”. In some instances the superposed theoretical model arms pass through small regions devoid of spiral arm tracers. Some models are used for illustration purposes in a figure, to show a reasonable likeness, but not to do a proper fit to one model—where one can see a “likely match”. We employ all recent researches offering “pieces” of the galactic disk, making use a “relative weight”, and attempt a re-construction of the pieces in order to get a better “overall” view.
Some distance methods have biases (neglecting dust patches incorrectly implies a more distant object) and other methods have biases (neglecting corrective terms in stellar proper motions imply a closer object), while some methods have random biases (neglecting a positive or negative velocity shock jump in kinematic distances implies a more distant or closer object).
Earlier tabular results were published in five blocks of 15 to 20 each, by Vallée [1-4] (respectively papers I to IV). Statistical results were obtained from these blocks of 15 to 20 entries to look for time variations [5]. Section 2 of this paper (V) presents the latest two blocks, each between 15 and 20 entries of published spiral arm researches since 2008.
Section 3 presents the latest cartographic modelling of the arms. The preponderance or not of the Sagittarius arm is discussed in Section 4, followed by a Conclusion (Section 5).
2. Data, Analysis and Evaluation
Here we attempt to analyse and evaluate and then assign a value (1, 2, 3, with best =3) to some recently published results, knowing the caveats mentioned above (specific areas, evolution, adaptations). The weighting is mostly a measure of quality (not quantity), as befit a meta-study. Lowest/poorest weight (1) is given to dust-affected measurements, because of incomplete corrections due to irregular dust patches that have an impact on distance determinations, and because some optical features may not be physically real or their appearance may be affected by an uneven angular distribution of dust reddening or patchy interstellar extinction. Top/best weight (3) is given for simple methods with the least number of assumptions, such as the parallax method or the arm tangents method. Medium/in-between weight (2) is given to all other methods, notably radial-velocity-based methods that are often affected by shocked gas causing local velocity jumps, while there are imprecision in the assumed LSR velocity for the Sun.
Tables 1 and 2 assemble the relevant results from recent studies on the spiral arms in the Milky Way since 2008. As in I to IV, we estimated a relative weight between 1 and 3. It is appropriate to average across all methods, as done in the last rows of Tables 1 and 2; in practice (see I to IV), the averages for weight = 3 data and for unweighted data are still very similar (not shown here, but within 1 or 2 s.d.m.).
Below, some additional qualitative comments are offered on some of the recently published results, where needed or appropriate.
Churchwell et al. [6] (their Figure 16) basically agreed with Vallée [4] (his Figure 1), except near the central Galactic double bar. They proposed different locations for the 3-kpc-arm and the start of the Norma arm (10˚ > long >0˚, close in space and velocity), while others do not find clear evidence to separate them [4] (Occam’s razor). Also, there is a well-defined observed tangent for the “start of the Perseus arm” at long = 339˚ (Table 2 in [4]), yet in [6] it is assumed to be part of the displaced and deformed 3-kpc-arm (too bent to mesh with the start of the Perseus arm). A third lack of agreement with [6] is that the Sagittarius arm at longitude l > 0˚ seems to mesh tangentially with the local Orion Spur rather than with the Carina arm at longitude l < 360˚.
Gao et al. [7] found that the mean 240 mm DIRBE emission peaks towards the tangents to the four spiral arms, while the mean extinction A3.6/AKs is dipping towards the tangents to the four spiral arms (both in their Figure 8). Such a change could suggest larger grain sizes and higher starlight intensities in spiral arms.
Table 1. Recent studies of spiral arms in the Milky Way (2008-2009).
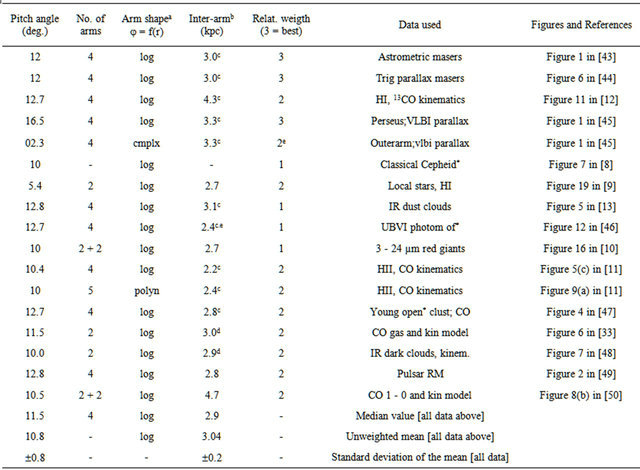
(a) j = f(r) means the azimuthal angle j follows a function of the radius r of the form f, where f is usually logarithmic, or if not, then polynomial or complex or ring. (b) distance between Perseus arm and Sagittarius arm, near the sun’s location. (c) corrected by assuming 8.0 kpc for the Sun-GC distance (not the 8.5 or 10 kpc used). (d) half of distance between 2 distant arms (Sagittarius to Cygnus; or Scutum to Perseus). (e) only 2 observational points used.
Table 2. Recent studies of spiral arms in the Milky Way (2010-2012).
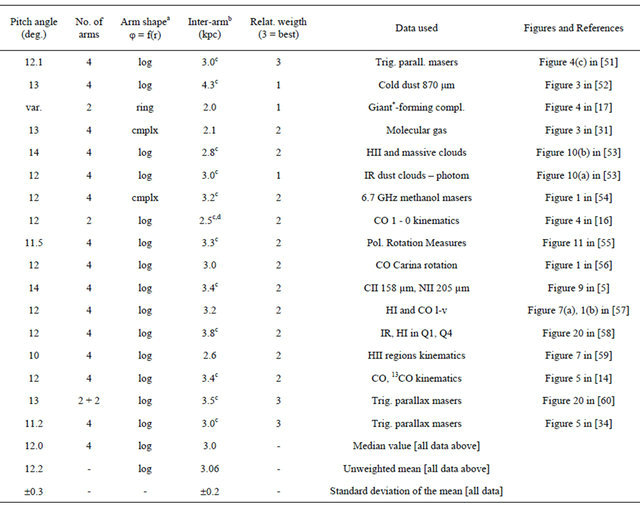
(a) j = f(r) means the azimuthal angle j follows a function of the radius r of the form f. (b) distance between Perseus arm and Sagittarius arm, near the sun’s location. (c) corrected by assuming 8.0 kpc for the Sun-GC distance (not the 8.5 or 10 kpc used). (d) half of distance between 2 distant arms (Sagittarius to Cygnus; or Scutum to Perseus).
Majaess et al. [8] plotted nearby Cepheids, with “feature A” (tied to the Sagittarius-Carina arm), F (tied to the Perseus arm), C (local spur), and others (B,D,E), but no arm was sketched. An eye-fit was employed to extract the basic parameters (see in Table 1).
Francis & Anderson [9] plotted model arms onto a map of local nearby stars and of the HI surface density. They found only 2 arms locally, with a much smaller pitch angle. Their Norma arm (l = 322˚) joins the “Perseus” arm (near l = 60˚; but there is no observed arm tangent there—see Table 2 of IV), then the local spur in which the Sun is located (thus the local spur becomes a major arm, contrary to published observations of its short length), joins the Carina-Sagittarius arm (at l = 270˚, but the observed arm tangent is at l = 284˚—see Table 2 of IV) and then joins the Cygnus arm. A list of the objects towards the local spur or armlet in 67˚ < l < 90˚ showed that all OB associations are within 2.2 kpc of the Sun, while all HII regions with |v(lsr)| less than 14 km/s are within 2.5 kpc of the Sun [10]—contrary to the model with a local spur becoming a long spiral arm as presented above.
Hou et al. [11] presented new models with different arm numbers (2 to 5) and pitch angles. We selected their Figure 5(c) (4 arms) and Figure 9(a) (5 arms) as representative. Their pitch angle values were averaged near the Sun on the Sun-GC line.
Roman-Duval et al. [12] identified in the first Galactic quadrant some 750 13CO 1 - 0 gas clouds as pertaining specifically to the Scutum and Sagittarius arms (their Figure 11 and Figure 12), showing that the mean separation of a cloud to the arm is typically 20% of the interarm distance (their Figure 13). Pitch angles are read from their figures.
Marshall et al. [13] computed the distance to IR dark clouds using genetic forward modeling, based on the extinction in two bands (J and Ks) versus the model expectation. They found (their Figure 5) that the locations of the IR dark clouds are seen to be concentrated along Galactic spiral arms (notably the Scutum-Crux arm). There is no modeling, yet their Figure suggests that their data and the model are compatible.
Roman-Duval et al. [14] noted that four issues limit the detection of the Galactic surface density of molecular gas in the Perseus arm (blending along the l-o-s; noncircular motions and kinematical models; completeness limit; low surface density), making the Perseus arm substantially unresolved from the Sun.
Steiman-Cameron et al. [5] noted the huge near-infrared absorption of evolved K and M stars located in the Sagittarius arm near l = 50˚, owing to material in front of the W51 cloud complex (their Section 4.1). Discounting the huge NIR absorption ends up discounting this arm, if one focuses only on K and M stars as spiral tracers. The issue of NIR absorption in the direction of the Sagittarius arm tangent was first pointed out by Benjamin et al. [15] and alluded to in Churchwell et al. [6].
Dame and Thaddeus [16] found the Scutum-Crux-Centaurus arm in galactic longitudes 13˚ < l < 55˚, corresponding essentially to the “blue” segment at the bottom of Figure 2 here. They found this “blue” arm segment from radial velocities –20 km/s (l = 13˚) to –84 km/s (l = 55˚), as essentially predicted earlier in Figures 2(a) and 3(a) in Vallée [4]. Their distance determination of 21 kpc (based on Rsun = 10 kpc) scales back to 17 kpc (using a modern value of Rsun = 8 kpc), as essentially predicted in Figure 2(a) in Vallée [4] for this “blue” arm.
Mel’nik and Rautiainen [17] offered ring-type arms (their Figure 4), where special viewings can lead to the appearance of spiral-like ascending or descending segments (their Figure 2).
The most useful effect of the data presented in Tables 1 and 2 is to place their results in a more general context, allowing a standardized presentation and statistics to be done. The statistical averages over time of blocks of arm parameters show a convergence with time [5] (their Section 4).
Figure 1 shows the “apparent” evolution with time of the inter-arm between Perseus and Sagittarius, for a line going through the Sun’s location. The unweighted mean value is shown for each block in I to V (this paper). While earlier blocks show larger values near 3.5 kpc, the more recent blocks show a mean value near 3.0 kpc.
3. Application—Global Cartographic Reconstruction Since the distance of the Sun to the Galactic Center [GC] was reduced from the 1964 IAU standard of 10 kpc to the 1985 IAU standard of 8.5 kpc [18], there have been calls for another reduction; some of the recent astrometric and other high-reliability data are listed here (this list is not complete).
Astrometric data for S2 by Gillessen et al. [19] gave 8.28 kpc. Groenewegen et al. [20] found 7.94 kpc using Type II Cepheids and RR Lyrae stars. Ghez et al. [21] used astrometry and radial velocity data for the orbit of the S0-2 star around the GC, and found 7.96 kpc using some orbital assumptions. Reid et al. [22] found 7.9 kpc, via a trigonometric parallax of SgrB2. Eisenhauer et al. [23] used proper motions and radial velocities of the S2 stellar orbit in the central light-month, obtaining a value of 7.6 kpc; this was changed to 7.7 kpc, when corrected for relativistic effects [24]. Nishiyama et al. [25] found 7.52 kpc, using IR photometry of bulge red clump stars. Thus a value between 7.8 kpc and 8.0 kpc is possible.
Stars within 5 kpc of the center of the Milky Way are not uniformly distributed. Inner spiral arms are seen tangentially at l = 328˚ (Norma or 3-kpc-arm at l = –32˚) and at l = 339˚ (“start of Perseus arm” at l = –21˚) on one side, and at l = 32˚ (Scutum-Crux arm) on the other side (as tabulated in Table 2 of IV). In addition to the inner spiral arms, one or more central “bars” have been observed. Cabrera-Lavers et al. [26] used red-clump NIR stellar population to deduce a bar at PA = 42˚ from the Sun-GC line (up to longitude l = 28˚ or 4.0 kpc long) and another bar at PA = 24˚ (up to l = 10˚ or 2.5 kpc). On the opposite point of view, Martinez-Valpuesta and Gerhard [27] argued that a single structure can explain the appearance of two bars (one thin and long, one thick and short), using a boxy bulge with a curved leading bend at the end (their Figure 1).
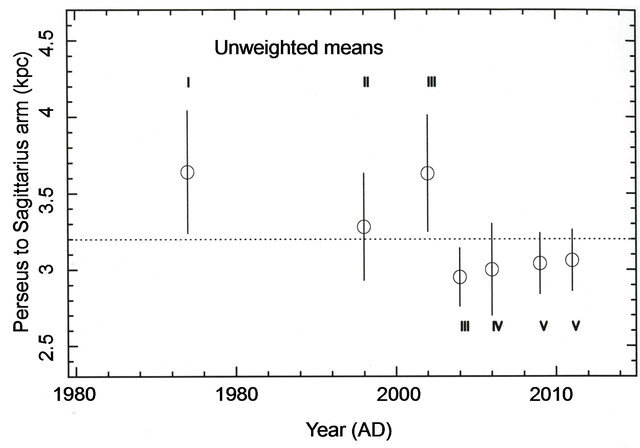
Figure 1. Unweighted mean values showing the inter-arm separation between Perseus and Sagittarius, for a line going through the Sun’s location. The 7 data values come from successive and roughly equal blocks, given in I, II, [III, III], IV, [V, V]. The early data averaged 3.5 kpc, while the recent data converge near 3.0 kpc. A demarcation (dotted) line is shown at 3.2 kpc.
Over time, we developed a fitting technique to incurporate all the observations obtained from many sources, telescopes, and filters (see equations in I, II, II, IV). Earlier results were published successively in blocks of 15 to 20 each, by Vallée [1-4]. Using as inputs the arm pitch, arm number, arm shape and Rsun, one can update the earlier cartographic/logarithmic model of the Milky Way’s disk. Our 4 model inputs are: pitch angle p = 12.8˚, m = 4 arms, logarithmic shape, and Rsun = 7.8 kpc. In doing so, we took account of the earlier and current results [e.g., a representative pitch of 12.8˚ taken from successive mean values of 11.6 (I), 11.7 (II), 12.4 and 13.5 (III), 13.5 (IV), 10.8 and 12.2 (here)].
The model fit has to correctly predict eight outputs, within their errors: the 6 arm tangents (e.g., mean values in Table 2 in IV), the inter-arm separation (e.g., Tables 1 and 2), as well as the triangulated distance of 1.95 kpc to W3(OH) at Galactic longitude l = 134˚ [28]. There is a “visual” fit involved, to get each arm location to satisfy all the many constraints (especially the observed arm tangents; this is not a brute least-squares fit).
The output values are ro = 2.1 ± 0.1 kpc and qo = –20˚ ± 5˚, where the radius r and angle q refer to the beginning of a spiral arm (at a non-zero radial distance from the GC and at a non-zero angle from the sun-GC line); a model arm spirals toward a smaller galactic radius as one proceeds to a greater galactic longitude, as defined in I. The new cartographic model fit yields:
• an inter-arm near the sun of 2.8 kpc• a distance to W3(OH) between 2.0 kpc and 1.9 kpc, as well as• a fit (within their rms error) to the 6 observed arm tangents (Table 2 in IV).
Given the inter-arm separation near 3.0 kpc near the sun (Figure 1), and the arm tangents with an rms near 3˚ (Table 2 in IV), our model cannot match the distance of the Sun to W3(OH) to a precision better than 0.1 kpc, given that the arm width has not been observationally defined in general. Some arm widths could be defined for a specific arm tracer, to the half-intensity level (e.g., HI), and could grow with the galactic radius.
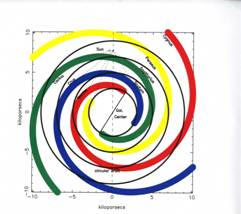
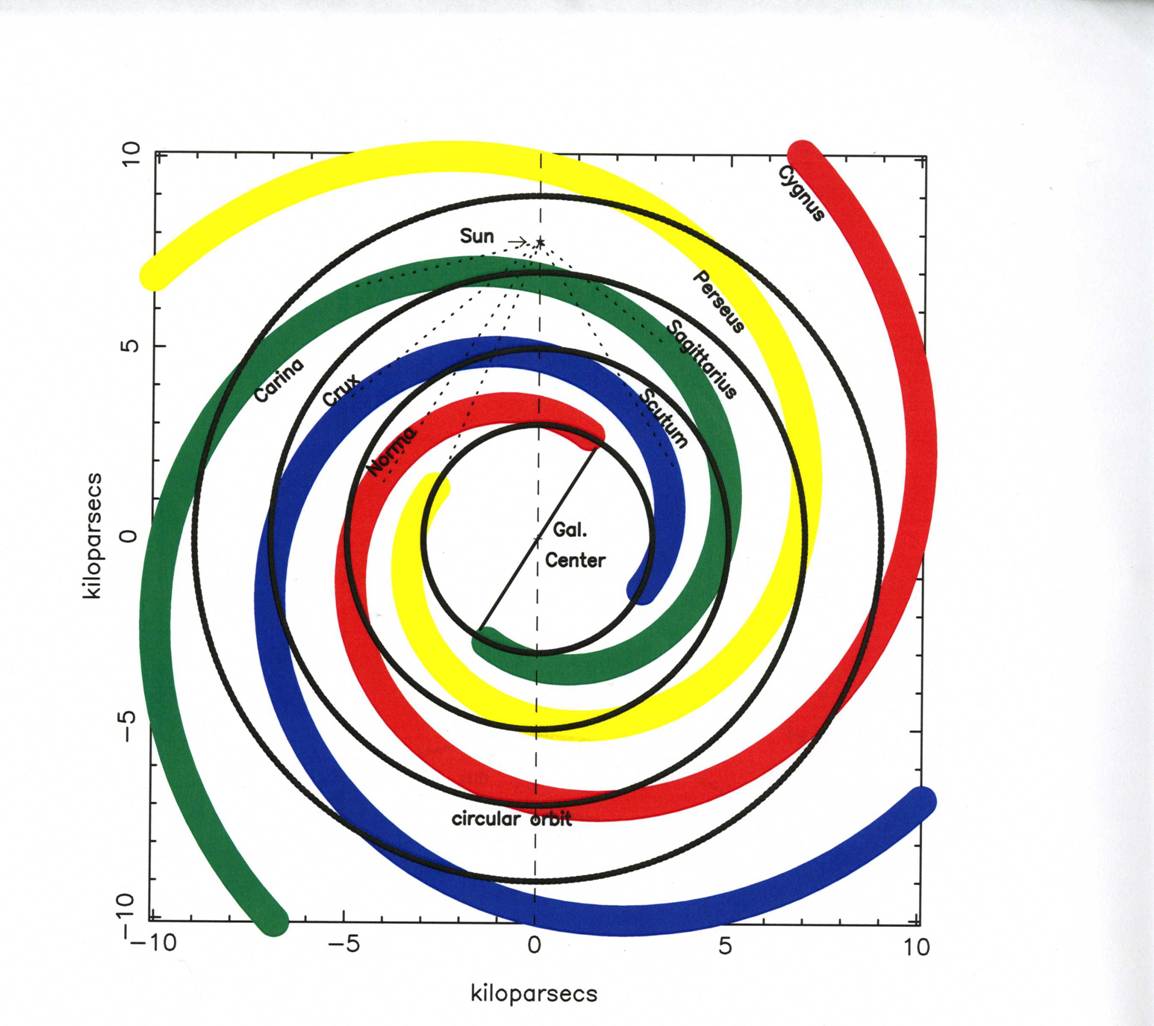
Figure 2 shows an updated cartographic map, with the observational tangents shown as dashed lines darting from the Sun (Table 2 in IV). The Perseus arm in the inner Galaxy may be a component of the pseudo “molecular ring” encompassing the origins of 4 spiral arms (Section 3.2 in IV), supporting the view that the Sagittarius arm is an equal arm.
In Figure 2, the generally assumed idealized circular orbital gas paths around the Galactic Center are shown as black circles, at various Galactic radii. Of course, nearly all orbits are probably slightly elliptical, and not purely circular (but we still do not know the eccentricity of the Sun’s orbit around the GC). Here, we assume the basic

|
Figure 2. Best two-dimensional, up-to-date idealized cartographic run. Dashed lines show the actual arm tangents obtained from observations of gas, dust and stars (Table 2 in IV). The ideal circular orbital paths around the Galactic Center, for the gas, stars and magnetic field, are shown as black circles at various Galactic radii.
assumption of symmetric and identical logarithmic arms. Elsewhere, a look at other spiral galaxies shows some deformations (flocculence was discussed in Section 3 of I), albeit the logarithmic form remains a good basic assumption for most spiral galaxies (the logarithmic form was discussed in Section 3 of II). Our perspective from inside the disk of the Milky Way makes it difficult at this stage to get a greater precision (see for spurs, fingers, ring).
Are there different pitch angles? The spiral structure of the Milky Way most probably will deviate somewhat from the ideal model above, notably with some spurs or armlets (as seen in some spiral galaxies) at differing pitch angles, and a deviation from a pure logarithmic form (although the logarithmic form is often adequately employed for many spiral galaxies) such as some deviation in pitch angle with Galactic radius.
Is there an inner ring or not? We argued against of full 4-kpc-ring encompassing the origins of the 4 spiral arms (Section 3.2 in IV), because a poor angular resolution and/or the signal sensitivity will hide the start of the 4 spiral arms at their specified galactic longitudes. Dame and Thaddeus [29] proposed the tangents to the –3 kpc arm (behind the Galactic Center) to be at l = ±23˚, on the basis of other data (taken before 1980). Since the l = –22˚ arm already belongs to the “start of the Perseus arm” (see Table 2 in IV), then a ring is not necessary, while the l = +23.5˚ arm is at the end of one bar on this side of the GC.
Are there fingers or not? Gas velocity jumps are likely to occur at spiral arm shocks. This has been seen already in Galactic maps made from HI kinematical models employing pure circular rotation around the Galactic Center (e.g, Figure 4(a) in [30]), showing “density fingers” pointing to the Sun. These radial fingers pointing to the Sun have been referred to as “fingers of God” (e.g., [31]) and are unphysical. To show this, Baba et al. [32] (their Section 4.3) employed a numerical code to set the appearance of the Milky Way, using typical stellar velocity deviations by 10% from circular velocity (their Figure 10(a)). They then re-computed a new map using the kinematic distance from the line-of-sight velocity measured at the sun, assuming an ideal circular velocity (their Figure 10(b)); the resulting changed map showed many non-physical “density fingers” pointing to the Sun. In a similar vein, Pohl et al. [33] (their Section 3) employed a numerical code to fix the appearance of the Milky Way, using actual model velocities (their Figure 4(a)) and reconstructed using circular velocity (their Figure 4(b), and their Equation 7), resulting in “artifacts” O and W (density fingers pointing away from the Sun).
4. Application: The Position (Distance) and Importance (Arm Width) of the Sagittarius Arm, and the Orbital Streamlines across It
4.1. Position
What is the position of the Sagittarius arm, in longitude and distance? A lack of a full and complete calibration can undermine a distance determination (giving a larger error than the quoted errors). For any spiral arm, it would be important to include all tracers to get its tangential longitude as seen from the Sun (Table 2 in IV).
For example, some assert that the Sagittarius arm’s position was incorrectly modeled or calibrated. Sato et al. [34] (their Section 5.2) noted that the location [in the longitude range 30˚ to 70˚] and the radial distance in that region of the Sagittarius arm has been changed (by up to several degrees in longitude and up to 50% in distance) in earlier standard well-used HII-based models.
One notes that the quoted distance to the Sagittarius arm towards longitude 330˚ can vary depending on the calibration used. Thus at l = 330˚, the Sagittarius arm is observed at 1.9 kpc in Figure 9 of [35], while it is observed at 1.1 kpc in Figure 2 of [36]. Such a huge change is attributed to the use of Mv-Mk calibrations versus the use of uvbyb calibrations [37].
4.2. Arm Width
What is the width of the Sagittarius arm, relative to other nearby arms? Is the Sagittarius arm roughly equal to other nearby arms? Stellar complexes located along a nearby longitudinal segment of a spiral arm may “alternate” with gaseous cloud complexes (without stars) at other distant longitude segments along the same arm. Which complexes we detect glaringly may depend on the Sun’s proximity to the various segments in the arm. Using only on a few arm tracers can undermine the “degree of importance” of each spiral arm.
For example, some assert that the Sagittarius arm and the Norma arm are “major” while the Perseus arm and the Scutum-Crux arm are “minor”; thus the Sagittarius arm is very prominent in radio molecular data [12,33], and in the distribution of optical classical Cepheid stars around the sun [8].
Others assert that the Sagittarius arm is “minor”, while the Perseus arm and the Scutum-Crux arm are “major”; thus the Perseus arm and the Scutum-Crux arm are best seen in red giant stars [10] (their Figure 16) and [38] (his Figure 1). They assert that the Sagittarius arm is “minor” because it is not prominent in IR data and lacking observed old K and M stars (although biased due to massive extinction by dust).
Thus importance (arm width) differs depending on the tracers selected, and arm position (distance) differs depending on selected calibrations; this suggests that a broader view encompassing all arm tracers should be used to estimate the overall arm importance (arm width). Doing so suggests that all arms run the gamut from minor to major, and thus all should be nearly equal in importance (arm width).
4.3. Orbital Streamlines
From an experimental/observational perspective, one can separate these models into four “groups” and ranked according to the increasing importance of turbulence: 1) flux-freezing is denied everywhere in the interstellar medium at scales beyond a few kpc, implying that the magnetic field lines are not be aligned with the gas velocities; 2) flux-freezing is applied everywhere in the interstellar medium, implying that magnetic field lines aligned with gas velocities; 3) the physical conditions in our Galaxy are employed in 3-dim. MHD smooth-particle hydrodynamical [SPH] simulations [39,40], implying fluxfreezing; 4) a galactic dynamo model is used, implying no galactic orbital gas streamlines around the Milky Way’s nucleus (for a recent review, see Section 9 in [41]. Here in the following, we have chosen flux-freezing groups (except during the passage through a spiral arm shock) in our preferred interpretation of and inference from the latest observational data (Tables 1 and 2 and Figure 2), and also in the discussion and explanation as sketched below.
a) Two-arm model. When the orbit of gas and dust re-enters a spiral arm, a shocked gas is likely to ensue. Roberts [42] (his Figure 3) showed the predicted orbital streamline as a “pointed oval”, with the sharp turning point located at the spiral arm location. His radial compression is Dr = 0.14 r, for an orbit reaching a maximum distance r. If there are only two “major” spiral arms (taken here as the Sagittarius-Carina arm and the NormaCygnus arm), there is a pitch angle change at each of these two major arms, but not at the other two minor arms. A sharp turn is constructed every 180˚ in an orbit. For a rough sketch of such a non-circular orbit with a “pointed oval”, see Vallée [41] (his Figure 36, with Sagittarius as one of the 2 major arms).
b) Four-arm model. We estimated the re-entry points in the Sagittarius-Carina arm for ideal circular orbits at various radii, with a radial compression of 10%. Measuring the position angle at the GC, from the GC-Sun line, the 9-kpc-radius orbit intersect the arm at PA = 73˚ to the left, the 7-kpc-radius orbit at PA = 13˚ to the left, and the 5-kpc-radis orbit at PA = 73˚ to the right. Here, the re-entry points in the Sagittarius—Carina arm anchors a sharp turn indicated every 90˚ in a galactic orbit. A rough sketch of such a non-circular orbit becomes a “4-segment spiral”—see Vallée [41] (his Figure 37, with Sagittarius as one of the 4 major arms).
5. Conclusions
We assembled recent positional data on the Milky Way’s spiral arms since early 2008 and classified their methods and the arm parameters, performed some statistics, and presented a reconstruction of the idealized galactic map.
We also examine the importance (width) and location (distance) of the Sagittarius arm, depending on the number of ¨equal¨ arms (using all tracers) or of “major vs minor” arms (selecting only a few tracers), and possible implications.
Our interpretation for all the recent data (Table 1; Table 2) favors the following:
• a four-arm non-circular spiral pattern for the Milky Way (Figure 2)
• the Sagittarius arm being likely an equal arm (Section 4)
• the inter-arm separation at the Sun’s location converging near 3.0 kpc (Figure 1).
We emphasize that these conclusions encompass all the data, and thus can vary somewhat from the results of data obtained from a single filter (only CO data, say).
A rough sketch of a non-circular orbit for a star in the ensuing gravitational potential could be a “4-segment spiral” – see Vallée [41] (his Figure 37).
6. Acknowledgements
The figure production made use of the PGPLOT software at the NRC in Victoria.
REFERENCES
- J. P. Vallée, “The Milky Way’s Spiral Arms Traced by Magnetic Fields, Dust, Gas, and Stars [Paper I],” Astrophysical Journal, Vol. 454, No. 3, 1995, 1995, pp. 119- 124.
- J. P. Vallée, “Metastudy of the Spiral Structure of Our Home Galaxy [Paper II],” Astrophysical Journal, Vol. 566, No. 1, 2002, pp. 261-266. doi:10.1086/337988
- J. P. Vallée, “The Spiral Arms and Inter-arm Separation of the Milky Way: An Updated Statistical Study [Paper III],” Astrophysical Journal, Vol. 130, No. 2, 2005, pp. 569-575.
- J. P. Vallée, “New Velocimetry and Revised Cartography of the Spiral Arms in the Milky WAY—A Consistent Symbiosis [Paper IV],” Astrophysical Journal, Vol. 135, No. 4, 2008, pp. 1301-1310.
- T. Y. Steiman-Cameron, M. Wolfire and D. Hollenbach, “COBE and the Galactic Interstellar Medium: Geometry of the Spiral Arms from FIR Cooling Lines,” Astrophysical Journal, Vol. 722, No. 2, 2010, pp. 1460-1473. doi:10.1088/0004-637X/722/2/1460
- E. Churchwell, B. L. Babler, M. R. Meade, B. A. Whitney, R. Benjamin, R. Indebetouw, C. Cyganowski, T. P. Robitaille, M. Povich, C. Watson and S. Bracker, “ The Spitzer/GLIMPSE Surveys: A New View of the Milky Way,” Publications of the Astronomical Society of the Pacific, Vol. 121, No. 877, 2009, pp. 213-230. doi:10.1086/597811
- J. Gao, B. W. Jiang and A. Li, “Mid-Infrared Extinction and its Variation with Galactic Longitude,” Astrophysical Journal, Vol. 707, No. 1, 2009, pp. 89-102. doi:10.1088/0004-637X/707/1/89
- D. J. Majaess, D. G. Turner and D. J. Lane, “Characteristics of the Galaxy according to Cepheids,” Monthly Notiuce of the Royal Astronomical Society, Vol. 398, No. 1, 2009, pp. 263-270.
- C. Francis and E. Anderson, “Galactic Spiral Structure,” Proceedings of the Royal Society A, Vol. 465, No. 2111, 2009, pp. 3425-3446. doi:10.1098/rspa.2009.0036
- B. Uyaniker, E. Fürst, W, Reich, B. Aschenbach and R. Wielebinski, “The Cygnus Superbubble Revisited,” Astronomy and Astrophysics, Vol. 371, No. 2, 2001, pp. 675-697.
- L. G. Hou, J. L. Han and W. B Shi, “The Spiral Structure of our Milky Way Galaxy,” Astronomy and Astrophysics, Vol. 499, No. 2, 2009, pp. 473-482.
- J. Roman-Duval, J. M. Jackson, M. Heyer, A. Johnson, J. Rathborne, R. Shah and R. Simon, “Kinematic Distances to Molecular Clouds Identified in the Galactic Ring Survey,” Astrophysical Journal, Vol. 699, No. 2, 2009, pp. 1153-1170. doi:10.1088/0004-637X/699/2/1153
- D. J. Marshall, G. Joncas and A. P. Jones, “Distribution and Characteristics of Infrared Dark Clouds Using Genetic Forward Modelling,” Astrophysical Journal, Vol. 706, No. 1, 2009, pp. 727-737. doi:10.1088/0004-637X/706/1/727
- J. Roman-Duval, J. M. Jackson, M. Heyer, J. Rathborne and R. Simon, “Physical Properties and Galactic Distribution of Molecular Clouds Identified in the Galactic Ring Survey,” Astrophysical Journal, Vol. 723, No. 1, 2010, pp. 492-507. doi:10.1088/0004-637X/723/1/492
- R. A. Benjamin, E. Churchwell, B. L. Babler, et al., “First GLIMPSE Results on the Stellar Structure of the Galaxy,” Astrophysical Journal, Vol. 630, No. 2, 2005, pp. L149-L152. doi:10.1086/491785
- T. M. Dame and P. Thaddeus, “A Molecular Spiral Arm in the Far Outer Galaxy,” Astrophysical Journal, Vol. 734, No. 1, 2011, pp. 1-4.
- A. M. Mel’nik and P. Rautiainen, “A Two-Component Outer Ring and Galactic Spiral Structure,” Mathematics & Physical Sciences, Vol. 418, No. 4, 2011, pp. 2508- 2518. doi:10.1111/j.1365-2966.2011.19641.x
- F. J. Kerr and D. Lynden-Bell, “Review of Galactic Constants,” Mathematics & Physical Sciences, Vol. 221, No. 2, 1986, pp.1023-2038.
- S. Gillessen, F. Eisenhauer, T. K. Fritz, H. Bartko, K. Dodds-Eden, O. Phuhl, T. Ott and R. Genzel, “The Orbit of the Star S2 Around SGR A* from Very Large Telescope and Keck Data,” Astrophysical Journal, Vol. 707, No. 2, 2009, pp. L114-L117. doi:10.1088/0004-637X/707/2/L114
- M. A. Groenewegen, A. Udalski and G. Bono, “The Distance to the Galactic Centre Based on Population II Cepheids and RR Lyrae Stars,” Astronomy and Astrophysics, Vol. 481, No. 2, 2008, pp. 441-448.
- A. M. Ghez, S. Salim, N. N. Weinberg, et al., “Measuring Distance and Properties of the Milky Way's Central Supermassive Black Hole with Stellar Orbits,” Astrophysical Journal, Vol. 689, No. 2, 2008, pp. 1044-1062. doi:10.1086/592738
- M. J. Reid, K. M. Menten, X. W. Zheng, A. Brunthaler and Y. Xu, “A Trigonometric Parallax of Sgr B2,” Astrophysical Journal, Vol. 705, No. 2, 2009, pp. 1548-1553. doi:10.1088/0004-637X/705/2/1548
- F. Eisenhauer, R. Genzel, et al., “SINFONI in the Galactic Center: Young Stars and Infrared Flares in the Central Light-Month,” Astrophysical Journal, Vol. 628, No. 1, 2005, pp. 246-259. doi:10.1086/430667
- S. Zucker, T. Alexander, S. Gillessen, F. Eisenhauer and R. Genzel, “Probing Post-Newtonian Physics near the Galactic Black Hole with Stellar Redshift Measurements,” Astrophysical Journal, Vol. 639, No. 1, 2006, pp. L21-L24. doi:10.1086/501436
- S. Nishiyama, T. Nagata, S. Sato, D. Kato, T. Nagayama, et al., “The Distance to the Galactic Center Derived from Infrared Photometry of Bulge Red Clump Stars,” Astrophysical Journal, Vol. 647, No. 2, 2006, pp. 1093-1098. doi:10.1086/505529
- A. Cabrera-Lavers, C. Gonzalez-Fernandez, F. Garzon, P. L. Hammersley and M. Lopez-Corredoira, “The Long Galactic Bar as Seen by UKIDSS Galactic Plane Survey,” Astronomy and Astrophysics, Vol. 491, No. 3, 2008, pp. 781-787.
- I. Martinez-Valpuesta and O. Gerhard, “Unifying A Boxy Bulge and Planar Long Bar in the Milky Way,” Astrophysical Journal, Vol. 734, No. 1, 2011, pp. 1-4.
- Y. Xu, M. J. Reid, X. W. Zheng and K. M. Menten, “The Distance to the Perseus Spiral Arm in the Milky Way,” Science, Vol. 311, No. 5757, 2006, pp. 54-57. doi:10.1126/science.1120914
- T. M. Dame and P. Thaddeus, “A New Spiral Arm of the Galaxy: The Far 3 kpc Arm,” Astrophysical Journal, Vol. 683, No. 2, 2008, pp. L143-L146. doi:10.1086/591669
- E. S. Levine, L. Blitz and C. Heiles, “The Spiral Structure of the Outer Milky Way in Hydrogen,” Science, Vol. 312, No. 5781, 2006, pp. 1773-1777. doi:10.1126/science.1128455
- P. Englmaier, M. Pohl and N. Bissantz, “The Milky Way Spiral Arm Pattern. 3D Distribution of Molecular Gas,” Mem. della Soc. Astron. Italiana, Vol. 18, No. 1, 2011, pp. 199-204.
- J. Baba, Y. Asaki, J. Makino, M. Miyoshi, T. R. Saitoh and K. Wada, “The Origin of Large Peculiar Motions of Star-Forming Regions and Spiral Structures of Our Galaxy” Astrophysical Journal, Vol. 706, No. 1, 2009, pp. 471- 481. doi:10.1088/0004-637X/706/1/471
- M. Pohl, P. Englmaier and N. Bissantz, “Three-Dimensional Distribution of Molecular Gas in the Barred Milky Way,” Astrophysical Journal, Vol. 677, No. 1, 2008, pp. 283-291. doi:10.1086/529004
- M. Sato, T. Hirota, M. J. Reid, M. Honma, H. Kobayashi, K. Iwadate, T. Miyaji and K. M. Shibata, “Distance to G14.33-0.64 in the Sagittarius Spiral Arm: H2O Maser Trigonometric Parallax with VERA,” Publications of the Astronomical Society of Japan, Vol. 62, No. 2, 2010, pp. 287-299.
- D. Russeil, C. Adami, P. Amram, E. Le Coarer, Y. M. Georgelin, M. Marcelin and Q. Parker, “A Deep Hα Survey of the Milky Way. VI. The l = 332˚ Area,” Astronomy and Astrophysics, Vol. 429, No. 2, 2005, pp. 497-507.
- D. Russeil, C. Adami and Y. M. Georgelin, “Revised Distances of Northern HII Regions,” Astronomy and Astrophysics, Vol. 470, No. 1, 2007, pp. 161-171.
- N. Kaltcheva, “Strömgren Hβ Photometry of O and B Stars in Norma,” Publications of the Astronomical Society of the Pacific, Vol. 121, No. 886, 2009, pp. 1326-1333. doi:10.1086/649431
- R. A. Benjamin, “The Spiral Structure of the Galaxy: Something Old, Something New...,” Astronomical Society of the Pacific, Vol. 387, No. 1, 2008, pp. 375-380.
- C. L. Dobbs and D. J. Price, “Magnetic Fields and the Dynamics of Spiral Galaxies,” Monthly Notiuce of the Royal Astronomical Society, Vol. 383, No. 2, 2008, pp. 497-512. doi:10.1111/j.1365-2966.2007.12591.x
- H. Kotarba, H. Lesch, K. Dolag, T. Naab, P. H. Johansson and F. A. Stasyszyn, “Magnetic Field Structure Due to the Global Velocity Field in Spiral Galaxies,” Mathematics & Physical Sciences, Vol. 397, No. 2, 2009, pp. 733-747. doi:10.1111/j.1365-2966.2009.15030.x
- J. P. Vallée, “Magnetic Fields in the Galactic Universe, as Observed in supErshells, Galaxies, Intergalactic and Cosmic Realms,” New Astronomy Reviews, Vol. 55, No. 3-4, 2011, pp. 91-154. doi:10.1016/j.newar.2011.01.002
- W. W. Roberts, “Theoretical Aspects of Galactic Research,” Vistas in Astronomy, Vol. 19, No. 1, 1975, pp. 91-109. doi:10.1016/0083-6656(75)90008-2
- K. Hachisuka, A. Brunthaler, K. M. Menten, M. J. Reid, Y. Hagiwara and N. Mochizuki, “The Distance to a Star-Forming Region in the Outer Arm of the Galaxy,” Astrophysical Journal, Vol. 696, No. 2, 2009, pp. 1981- 1986. doi:10.1088/0004-637X/696/2/1981
- A. Brunthaler, M. J. Reid, K. M. Menten, X. W. Zheng, L. Mosacadelli and Y. Xu, “Trigonometric Parallaxes of Massive Star-Forming Regions. V. G23.01-0.41 and G23.44-0.18,” Astrophysical Journal, Vol. 693, No. 1, 2009, pp. 424-429. doi:10.1088/0004-637X/693/1/424
- M. J. Reid, K. M. Menten, X. W. Zheng, A. Brunthaler, L. Moscadelli, et al., “Trigonometric Parallaxes of Massive Star-Forming Regions. VI. Galactic Structure, Fundamental Parameters, and Noncircular Motions,” Astrophysical Journal, Vol. 700, No. 1, 2009, pp. 137-148. doi:10.1088/0004-637X/700/1/137
- G. Carraro and E. Costa, “Searching for Spiral Features in the Outer Galactic Disk. The Field towards WR38 and WR38a,” Astronomy and Astrophysics, Vol. 493, No. 1, 2009, pp. 71-78.
- R. A. Vasquez, J. May, G. Carraro, L. Bronfman, A. Moitinho and G. Baume, “Spiral Structure in the Outer Galactic Disk. I. The Third Galactic Quadrant,” Astrophysical Journal, Vol. 672, No. 2, 2008, pp. 930-939. doi:10.1086/524003
- J. M. Jackson, S. C. Finn, J. M. Rathborne, E. T. Chambers and R. Simon, “The Galactic Distribution of Infrared Dark Clouds,” Astrophysical Journal, Vol. 680, No. 1, 2008, pp. 349-361. doi:10.1086/587539
- J. P. Vallée, “An Improved Magnetic Map of the Milky Way, with the Circularly Orbiting Gas and Magnetic Field Lines Crossing the Dusty Stellar Spiral Arms,” Astrophysical Journal, Vol. 681, No. 1, 2008, pp. 303-310. doi:10.1086/588577
- N. J. Rodriguez-Fernandez and F. Combes, “Gas Flow Models in the Milky Way Embedded Bars,” Astronomy and Astrophysics, Vol. 489, No. 1, 2008, pp. 115-133.
- A. Sanna, M. J. Reid, T. M. Dame, K. M. Menten, A. Brunthaler, L. Moscadelli, X. W. Zheng and Y. Xu, “Trigonometric Parallaxes of Massive Star-Forming Regions. IX. The Outer Arm in the First Quadrant,” Astrophysical Journal, Vol. 745, No. 1, 2012, pp. 82, 1-7.
- H. Beuther, J. Tackenberg, H. Linz, Th. Henning, F. Schuller, F. Wyrowski, P. Schilke, K. Menten, T. P. Robitaille, C. M. Walmsley, L. Bronfman, F. Motte, Q. Nguyen-Luong and S. Bontemps, “Galactic Structure Based on the ATLASGAL 870 μm Survey” Astrophysical Journal, Vol. 747, No. A43, 2012, pp. 1-8.
- D. Russeil, M. Pestalozzi, et al., “Giving Physical Significance to the Hi-GAL Data: Determining the Distance of Cold Dusty Cores in the Milky Way,” Astronomy and Astrophysics, Vol. 526, No. A151, 2011, pp. 1-20.
- J. A. Green, J. L.Caswell, N. M. McClure-Griffiths, A. Avison, S. L. Breen, M. G. Burton, S. P. Ellingsen, G. A. Fuller, M. D. Gray, M. Pestalozzi, M. A. Thompson and M. A. Voronkov, “Major Structures of the Inner Galaxy Delineated by 6.7 GHz Methanol Masers,” Astrophysical Journal, Vol. 733, No. 1, 2011, pp. 1-17. doi:10.1088/2041-8205/726/1/L1
- C. L. Van Eck, J. C. Brown, J. M. Stil, K. Rae, S. A. Mao, B. M. Gaensler, A. Shukurov, A. R. Taylor, M. Haverkorn, P. P. Kronberg and N. M. McClure-Griffiths, “Modeling the Magnetic Field in the Galactic Disk Using New Rotation Measure Observations from the Very Large Array,” Astrophysical Journal, Vol. 728, No. A97, 2011, pp. 1-32.
- Y. N. Efremov, “On the spiral structure of the Milky Way Galaxy,” Astronomy Reports, Vol. 55, No. 2, 2011, pp. 108-122. doi:10.1134/S1063772911020016
- J. Baba, T. R. Saitoh and K. Wada, “On the Interpretation of the l-v Features in the Milky Way Galaxy,” Publications of the Astronomical Society of the Japan, Vol. 62, No. 6, 2010, pp. 1413-1422.
- H. A. Ford, F. J. Lockman and N. M. McClure-Griffiths, “Milky Way Disk-Halo Transition in H I: Properties of the Cloud Population,” Astrophysical Journal, Vol. 722, No. 1, 2010, pp. 367-379. doi:10.1088/0004-637X/722/1/367
- T. Foster and B. Cooper, “Structure and Dynamics of the Milky Way: The Evolving Picture,” Astronomical Society of the Pacific Conference Series, Vol. 438, No. 1, 2010, pp. 16-30.
- [61] K. L. Rygl, A. Brunthaler, M. J. Reid, K. M. Menten, H. J. van Langevelde and Y. Xu, “ Trigonometric Parallaxes of 6.7 GHz Methanol Masers,” Astronomy and Astrophysics, Vol. 511, No. A2, 2010, pp. 1-17.


 hic (which is ideally a 500 dpi jpg, png or tif file, with all fonts embedded) because, in an MSW document, this method is somewhat more stable than directly inserting a picture.
hic (which is ideally a 500 dpi jpg, png or tif file, with all fonts embedded) because, in an MSW document, this method is somewhat more stable than directly inserting a picture.