International Journal of Astronomy and Astrophysics
Vol. 2 No. 2 (2012) , Article ID: 19740 , 6 pages DOI:10.4236/ijaa.2012.22011
Simultaneous Gravitational and Refractive Lensing
Applied Science Enterprise, Warszawa, Poland
Email: chylawt@wp.pl
Received November 18, 2011; revised February 22, 2012; accepted March 3, 2012
Keywords: Gravitational Lensing; Microlensing; Macrolensing; Refraction
ABSTRACT
The principal testing ground for general relativity is the observable Universe. Gravitational lensing is the leading observational technique that gives insight into the distribution of baryonic matter in the stellar, galactic and cosmological scale, as well as the distribution of dark matter and dark energy, due to their gravitational interaction. Interpretation of ever more precise observational data requires increasingly subtle analytical techniques. In this paper, I discuss a formalism that can handle a nonlinear superposition of gravitational and refractive lensing by a grouping of baryonic matter, dark matter and dark energy for a given distribution of those entities (i.e. for a given spacetime metric) and their refractive properties. The role of refraction in gravitational lensing is exemplified in the case of a microlensing event and a signature of such an effect is discussed.
1. Introduction
The two most challenging problems in general relativity are: quantization of the gravitational field, as a precondition for unification of gravity with the other three (quantized) interactions, and application of general relativity to investigation of the Universe. In this paper, I take on the latter endeavor by considering the problem of simultaneous gravitational and refractive lensing.
Gravitational lensing occurs where the lensing mass lies very close to geodesics that connect the luminous object and the observer; this phenomenon is often referred to as macrolensing or microlensing. Macrolensing images are classified either as strong lensing, where magnified multiple images of a luminous source are observed, or weak lensing that results in magnification and distortion of a single image. If the luminous source and the lens cannot be resolved, gravitational lensing manifests as a temporary increase in brightness of the lensed object, which is called a microlensing event.
The first multiple image of the gravitationally lensed quasar was observed in 1979 [1]. A number of very successful research programs, such as OGLE, MACHO, EROS, MOA, mFUN and PLANET have been specifically designed to detect and analyze microlensing events [2-7].
The lensing effect is usually interpreted as a purely general relativistic phenomenon. Refractive lensing by cold gas clouds has also been considered [8,9]. However, one can think of a number of situations, where the total lensing effect is a (possibly nonlinear) superposition of the gravitational component and the refractive one. This may occur where the lensing object possesses an extended gaseous envelope, where lensing is caused by a massive molecular cloud, by a gas-rich galaxy, a compact body embedded in the plasma cloud or a compact body that generates strong magnetic field. These situations can be handled with a theory of simultaneous gravitational and refractive lensing. The formalism allows the lensing object to comprise baryonic matter, dark matter and dark energy that together contribute to the spacetime metric and to the effective refractive index.
In the following section I discuss principles of combined gravitational and refractive lensing. Next, I consider a microlensing event caused by a superposition of gravity and refraction and discuss some physical aspects of the refractive component of lensing. A brief general conclusion completes this work.
2. Principles of Combined Gravitational and Refractive Lensing
From the analytical point of view, the key difference between gravitational lensing and refractive lensing is that the first one is achromatic and the second one is frequency-dependent. To examine and possibly single out the two components of the total lensing, the microlensing events and macrolensing images have to be observed in a wide range of the electromagnetic spectrum, from radiofrequencies to the UV range.
In the classical approach, propagation of light rays in the geometrical optics regime is governed by the Fermat principle, which silently assumes that the frequency of the light ray is constant along its virtual path; that is because the quantum and relativistic phenomena that affect the local values of frequency of light rays were unknown at the times of Fermat. To account for possible changes in frequency (e.g. due to the gravitational redshift/blueshift) in the geometrical optics regime, one has to start off from the principle of least action for the electromagnetic field, from which the variation principle for variable-frequency (VF) light rays can be derived. The new extremum principle, which governs propagation of VF light rays in the geometrical optics regime, reads [10]
 (1)
(1)
where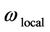 ,
,  ,
,  are the local standard values of (angular) frequency, time and distance along the virtual path of the light ray, respectively, measured with local standard (atomic) clocks according to the definition of the second and the meter, and
are the local standard values of (angular) frequency, time and distance along the virtual path of the light ray, respectively, measured with local standard (atomic) clocks according to the definition of the second and the meter, and  is the local value of the refractive index measured with the same local standard instruments. The new variation principle is valid irrespective of the kind of interaction that affects frequency of the light ray.
is the local value of the refractive index measured with the same local standard instruments. The new variation principle is valid irrespective of the kind of interaction that affects frequency of the light ray.
From the variation principle in Equation (1) one can derive the differential equations that govern propagation of light rays affected by a nonlinear superposition of gravity and refraction in the static spacetime [11]
 (2)
(2)
where the effective connection coefficients are
 (3)
(3)
and
 (4)
(4)
with
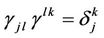 (5)
(5)
and
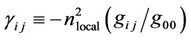 (6)
(6)
where  are elements of the spacetime metric with signature
are elements of the spacetime metric with signature  and
and .
.
Equation (2) shows that the actual path of the light ray in the general relativistic environment is given by the effective “geodesic” on a 3d manifold shaped by the nonlinear superposition of gravity and refractive properties of the medium, see Equation (6), in which the light ray propagates. This formalism is capable of handling the whole range of situations, from gravity dominated lensing (including a black hole as a microlens) to refraction dominated lensing; in principle, it applies both to microlensing events and macrolensing images.
In the case of low refraction and weak gravitational field, the effective connection coefficients  can be expanded into the fast converging series, where only the leading gravitational and refractive terms have to be taken into account; then, in the linear field approximation, the gravitational lensing and the refractive lensing become additive effects.
can be expanded into the fast converging series, where only the leading gravitational and refractive terms have to be taken into account; then, in the linear field approximation, the gravitational lensing and the refractive lensing become additive effects.
3. A Microlensing Event Due to Gravity and Refraction
The microlensing technique was advocated by Paczyński for detecting brown dwarfs in the galactic halo in an attempt to estimate their contribution to the dark matter [12]. Presently, microlensing has become one of the most prolific sources of information in observational astronomy and astrophysics.
Low temperature objects are hardly (or not at all) visible by the use of conventional methods; even more so are their atmospheres. The formalism discussed in the previous section makes possible exploration of gaseous envelopes of invisible objects acting as gravitational lenses.
In absence of lensing, spectral intensity of the photon flux  of a stable, point-like source is constant in time. Where microlensing is a purely gravitational, achromatic effect, the temporal dependence of the normalized (relative) spectral intensity
of a stable, point-like source is constant in time. Where microlensing is a purely gravitational, achromatic effect, the temporal dependence of the normalized (relative) spectral intensity  is the same for all frequencies n, from the RF to the UV band. Since the refractive component of lensing is frequency-dependent, the quantity
is the same for all frequencies n, from the RF to the UV band. Since the refractive component of lensing is frequency-dependent, the quantity 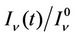 for combined gravitational and refractive lensing varies with frequency, as shown in Figure 1.
for combined gravitational and refractive lensing varies with frequency, as shown in Figure 1.
Brightness curves observed at different frequencies carry information on the size, density, chemical composition of the gaseous envelope and the magnetic field of the lensing object, although the object may not be directly visible.
The inverse lensing problem of (supposedly) purely gravitational lensing produces non-unique solutions, see e.g. the Appendix in [3]; where additional effects are taken into account, such as refraction or limb darkening of an extended luminous source, the number of possible models and fitting parameters increases, which makes the problem even more challenging. The uncertainty of interpretation of observational data can be minimized by taking into consideration spectroscopic and photometric information collected in a wide range of the electromagnetic spectrum, as those data constitute additional constraints on the choice of the assumed model.
Refraction can produce an asymmetric, sharp peak on the relative brightness curve, but it can also decrease brightness. To notice such short-time perturbations, short sampling time intervals are necessary; otherwise, averaging produces only a small irregularity on the standard

Figure 1. An example of microlensing of a point-like luminous source by a large object with a low-mass companion. Purely gravitational lensing results in the same temporal dependence of the relative spectral intensity Iv(t)/ for all frequencies (black curve). Refraction differentiates between the relative brightness curves registered at different frequencies (blue curve, red curve). The gaseous envelope of a highly magnetic companion object (e.g. a magnetar) can become birefringent, which may result in discernible doubling of the refraction peaks that perturbe the standard lensing curve.
for all frequencies (black curve). Refraction differentiates between the relative brightness curves registered at different frequencies (blue curve, red curve). The gaseous envelope of a highly magnetic companion object (e.g. a magnetar) can become birefringent, which may result in discernible doubling of the refraction peaks that perturbe the standard lensing curve.
brightness curve. To get a grasp on the peak, the sampling time interval should be at least 3 - 4 times less than the halfwidth of the peak. The refractive effect can be an alternative interpretation of some very sharp peaks on the brightness curves, which are presently modeled exclusively as caustic crossings.
Refraction enters the picture where the light beam traverses the gaseous envelope. In the case of microlensing, refraction occurs only where the light beam passes at the grazing distance from the lensing object, so that only a fraction of microlensing events can actually comprise the refractive component. Refraction in a microlensing event is accompanied by temporal changes in the (absorption) spectrum during lensing; if the luminous object cannot be treated as a point source, the picture gets complicated by limb darkening and spectral variability of the source.
In most lensing situations, refraction constitutes a small correction to purely gravitational lensing. Equations (2)-(6) imply that the contribution of refraction to deflection of light rays is favored by high values of the refractive index , the gradient
, the gradient , and dispersion
, and dispersion .
.
The refractive index of a medium depends on the strength of the magnetic field B; very high B of a lensing object, such as a magnetar, can polarize its gaseous envelope. The signature of such an effect is an increase in circular polarization of light during lensing and possible doubling of refractive peaks, because the medium subject to high B becomes circularly birefringent; this effect is frequency-dependent.
The gradient  may have (relatively) high value only in a thin layer of the lensing medium. It implies very narrow perturbations of the standard brightness curve and the necessity to shorten the sampling time intervals, which may be a significant technical challenge.
may have (relatively) high value only in a thin layer of the lensing medium. It implies very narrow perturbations of the standard brightness curve and the necessity to shorten the sampling time intervals, which may be a significant technical challenge.
Since the refractive component of lensing depends on dispersion , the role of refraction increases at frequencies approaching the edge of (absorption) spectral lines, compared to lensing at frequency bands far from resonant absorption.
, the role of refraction increases at frequencies approaching the edge of (absorption) spectral lines, compared to lensing at frequency bands far from resonant absorption.
4. Conclusions
Advancement in theoretical research and creation of new theories is inseparable from availability of hard experimental data and observational facts. Since there is no way to produce strong gravity in laboratory conditions, the theory of general relativity and gravitation is tested by observations of the Universe, which contains baryonic matter subject to extreme conditions and exotic inhabitants such as black holes, dark matter, dark energy and possibly other kinds of physical entities, such as the Higgs field [13-21].
In the past few decades, gravitational lensing has become one of principal sources of information on gravity in the cosmological realm, on the large scale structure of the Universe, hypothetical physical entities that shape the spacetime and properties of individual astronomical objects, such as stars and exosolar planets [22-26]. As the technological capabilities increase, ever more refined analytical tools are required.
The theory discussed in this paper allows including refraction into the analysis of gravitational lensing. In principle, it covers all situations (i.e. microlensing and macrolensing) as long as the notion of the refractive index in the general relativistic environment is valid. Interpretation of microlensing events and macrolensing images in terms of combined gravitational and refractive lensing is model-dependent; the inverse lensing problem requires observational constraints to limit the number of possible models and fitting parameters. Spectroscopic and photometric data at frequencies ranging from RF to UV can be instrumental in designing the lensing model and disentangling parameters of the lens and the lensing object.
REFERENCES
- D. Walsh, R. F. Carswell and R. J. Weymann, “0957 + 561 A, B: Twin Quasistellar Objects or Gravitational Lens?” Nature, Vol. 279, No. 5712, 1979, pp. 381-384. doi:10.1038/279381a0
- A. Udalski, M. Szymański, J. Kałużny, M. Kubiak, W. Krzemiński, M. Mateo, G. W. Preston and B. Paczyński, “The Optical Gravitational Lensing Experiment. Discovery of the First Candidate Microlensing Event in the Direction of the Galactic Bulge,” Acta Astronomica, Vol. 43, No. 3, 1993, pp. 289-294.
- M. Jaroszyński, J. Skowron, A. Udalski, M. Kubiak, M. K. Szymański, G. Pietrzyński, I. Soszyński, Ł. Wyrzykowski, K. Ulaczyk and R. Poleski, “Binary Lenses in OGLE-III EWS Database. Seasons 2006-2008,” Acta Astronomica, Vol. 60, No. 3, 2010, pp. 197-231.
- C. Alcock, R. A. Allsman, D. Alves, T. S. Axelrods, K. H. Bennett, et al., “The MACHO Project: 45 Candidate Microlensing Events from the First-Year Galactic Bulge Data,” The Astrophysical Journal, Vol. 479, No. 1, 1997, pp. 119-146. doi:10.1086/303851
- P. Tisserand, L. Guillou, C. Afonso, J. N. Albert, et al., “Limits on the MACHO Content of the Galactic Halo from EROS-2 Survey of the Magellanic Clouds,” Astronomy and Astrophysics, Vol. 469, No. 2, 2007, pp. 387-404. doi:10.1051/0004-6361:20066017
- S. Dong, F. Abe, G. Bolt, A. Udalski, et al., “Microlensing Event MOA-2007-BLG-400: Exhuming the Buried Signature of a Cool Jovian-Mass Planet,” The Astrophysical Journal, Vol. 698, No. 2, 2009, pp. 1826-1837.
- J. Janczak, F. Abe, J. H. An, T. Anguita, V. Batista, et al., “Sub-Saturn Planet MOA-2008-BLG-310Lb: Likely to Be in the Galactic Bulge,” The Astrophysical Journal, Vol. 711, No. 2, 2010, pp. 731-743. doi:10.1088/0004-637X/711/2/731
- B. T. Draine, “Lensing of Stars by Spherical Gas Clouds,” Astrophysical Journal Letters, Vol. 509, No. 1, 1998, pp. L41-L44. doi:10.1086/311751
- R. R. Rafikov and B. T. Draine, “Constraints on Cold H2 Clouds from Gravitational Microlensing Searches,” The Astrophysical Journal, Vol. 547, No. 1, 2001, pp. 207- 216. doi:10.1086/318355
- W. T. Chyla, “I. Geometrical Optics of Variable-Frequency Light Rays: Theoretical Basis,” Canadian Journal of Physics, Vol. 78, No. 8, 2000, pp. 721-745.
- W. T. Chyla, “III. Geometrical Optics of Variable-Frequency Light Rays in the General Relativistic Regime: Combined Gravitational and Refractive Lensing,” Canadian Journal of Physics, Vol. 78, No. 8, 2000, pp. 755-767. doi:10.1139/p00-021
- B. Paczyński, “Gravitational Microlensing by the Galactic Halo,” The Astrophysical Journal, Vol. 304, No. 1, 1986, pp. 1-5.
- R. S. Ellis, “Gravitational Lensing: A Unique Probe of Dark Matter and Dark Energy,” Philosophical Transactions of the Royal Society A, Vol. 368, No. 1914, 2010, pp. 967-987.
- T. Treu, “Strong Lensing by Galaxies,” Annual Review of Astronomy and Astrophysics, Vol. 48, No. 1, 2010, pp. 87-125. doi:10.1146/annurev-astro-081309-130924
- J. P. Uzan, “Tests of General Relativity on Astrophysical Scales,” General Relativity and Gravitation, Vol. 42, No. 9, 2010, pp. 2219-2246. doi:10.1007/s10714-010-1047-8
- A. Zakharov, “Lensing by Exotic Objects,” General Relativity and Gravitation, Vol. 42, No. 9, 2010, pp. 2301- 2322. doi:10.1007/s10714-010-1021-5
- B. Paczyński, “Is There a Black Hole in the Sky?” Nature, Vol. 321, No. 6068, 1986, pp. 419-420. doi:10.1038/321419a0
- V. Bozza, “Gravitational Lensing by Black Holes,” General Relativity and Gravitation, Vol. 42, No. 9, 2010, pp. 2269-2300. doi:10.1007/s10714-010-0988-2
- R. W. Schmidt and J. Wambsganss, “Quasar Microlensing,” General Relativity and Gravitation, Vol. 42, No. 9, 2010, pp. 2127-2150. doi:10.1007/s10714-010-0956-x
- P. Schneider, C. Kochanek and J. Wambsganss, “Gravitational Lensing: Strong, Weak and Micro,” Springer, Berlin, 2006.
- E. Gates, “Einstein’s Telescope: The Hunt for Dark Matter and Dark Energy in the Universe,” Norton, New York, 2009.
- D. M. Wittman, J. A. Tyson, D. Kirkman, I. Dell’Antonio and G. Bernstein, “Detection of Weak Gravitational Lensing Distortions of Distant Galaxies by Cosmic Dark Matter at Large Scales,” Nature, Vol. 405, No. 6783, 2000, pp. 143-148.
- D. Huterer, “Weak Lensing and Dark Energy,” Physical Review D, Vol. 65, No. 6, 2002, Article ID: 063001. doi:10.1103/PhysRevD.65.063001
- D. Clowe, M. Bradač, A. H. Gonzalez, M. Markevitch, S. W. Randall, C. Jones and D. Zaritsky, “A Direct Empirical Proof of the Existence of Dark Matter,” The Astrophysical Journal Letters, Vol. 648, No. 2, 2006, pp. L109- L113. doi:10.1086/508162
- D. Huterer, “Weak Lensing, Dark Matter and Dark Energy,” General Relativity and Gravitation, Vol. 42, No. 9, 2010, pp. 2177-2195. doi:10.1007/s10714-010-1051-z
- M. Dominik, “Studying Planet Populations by Gravitational Microlensing,” General Relativity and Gravitation, Vol. 42, No. 9, 2010, pp. 2075-2100. doi:10.1007/s10714-010-0930-7

