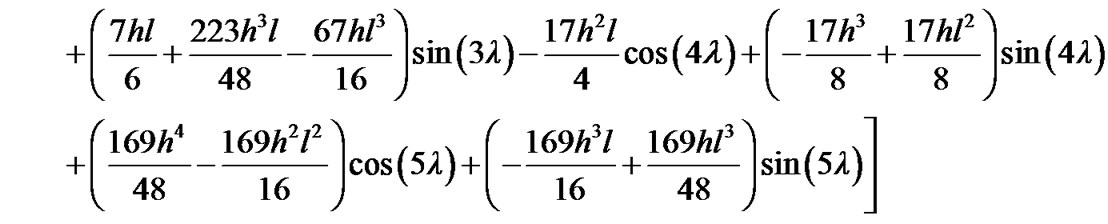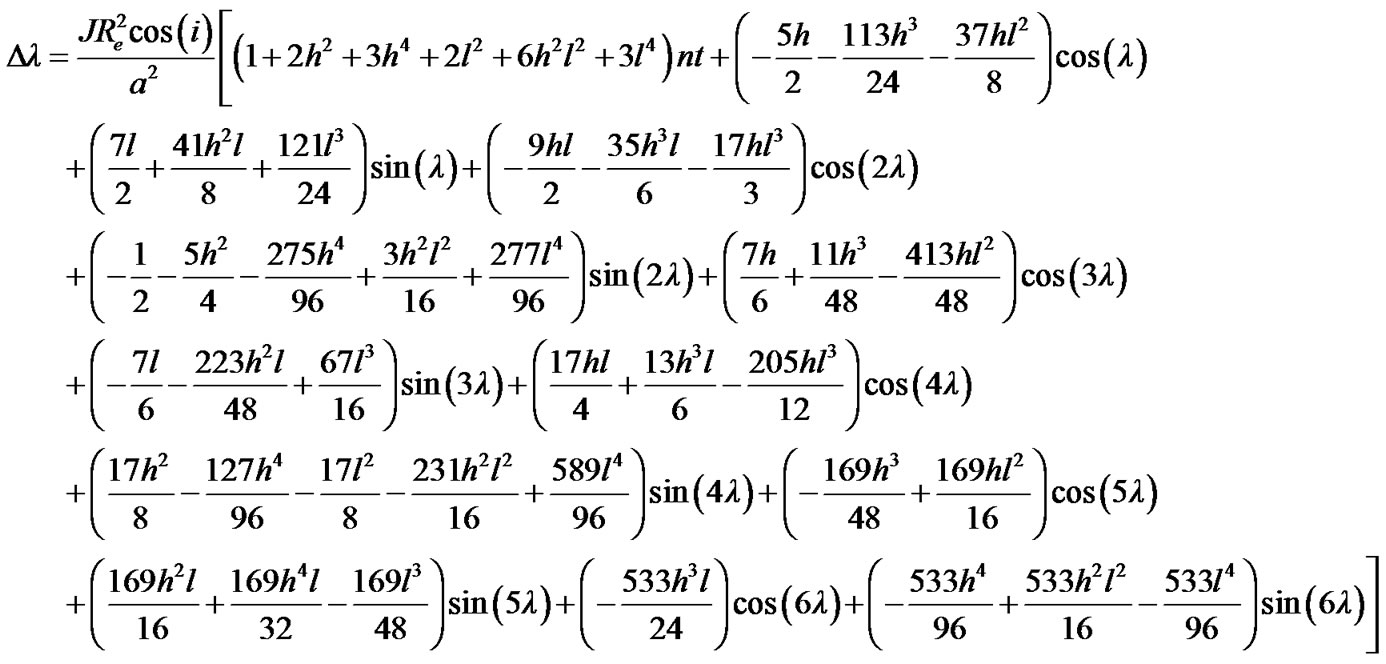International Journal of Astronomy and Astrophysics
Vol.1 No.3(2011), Article ID:7364,12 pages DOI:10.4236/ijaa.2011.13018
Short-Term Orbit Prediction with J2 and Mean Orbital Elements
1Applied Mathematics Division, Vikram Sarabhai Space Centre, Thiruvananthapuram, India
2Present Address: Department of Aerospace Engineering, School of Mechanical Sciences, Karunya University, Coimbatore, India
E-mail: sddgupta@gmail.com, m_xavierjamesraj@vssc.gov.in, ramkrishansharma@gmail.com
Received July 8, 2011; revised August 15, 2011; accepted August 26, 2011
Keywords: Perturbation Due to J2, Mean Orbital Elements, Short-Periodic Terms, Osculating Orbital Elements, Fourth Power in Eccentricity
Abstract
An analytical theory for calculating perturbations of the orbital elements of a satellite due to J2 to accuracy up to fourth power in eccentricity is developed. It is observed that there is significant improvement in all the orbital elements with the present theory over second-order theory. The theory is used for computing the mean orbital elements, which are found to be more accurate than the existing Bhatnagar and Taqvi’s theory (up to second power in eccentricity). Mean elements have a large number of practical applications.
1. Introduction
The fact that the Earth is not a true sphere is one of the important causes for the deviation of the orbits of the artificial satellites from undisturbed Keplerian ellipses, the largest perturbations in the motion of such satellites being due to the oblateness of the Earth. The standard osculating, i.e. instantaneously defined elements of an elliptic orbit are “a” (semi-major axis), “e” (eccentricity), “i” (inclination), “Ω” (right ascension of ascending node), “ω” (argument of perigee) and “M” (mean anomaly). The osculating element space is related to mean element space through the short-periodic variations which are combination of short-periodic terms of period less than the orbital period of the orbital elements and are functions of the perturbations present. If ζ is an osculating element and 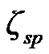 is the short-periodic variation in the corresponding element, then the mean element
is the short-periodic variation in the corresponding element, then the mean element  is related by
is related by 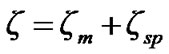 where
where 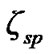 is the function of mean elements.
is the function of mean elements.
The motion of an artificial satellite in the axisymmetric field due to Earth’s low-degree harmonics has been recognized as the “main problem” in the theory of satellite orbits, and many solutions have been published. Some of the important contributions are due to Kozai [1], Brouwer [2], Chebotarev [3], Deprit and Rom [4], Aksnes [5], Liu [6], Kinoshita [7], Bhatnagar and Taqvi [8], Gooding [9]. Sharma [10] utilized the theories of Bhatnagar and Taqvi and Liu to compute the mean elements using the iterative scheme of Gooding [11] and made a comparison between them.
Chebotarev [3] generated analytical expressions for short-periodic terms with J2 specifically for near-circular orbits, by introducing the variables h = e·sinω, l = e·cosω in the Lagrange’s planetary equations and then computing the involved partial derivatives of the perturbing function R on the right hand side of the equations and then analytically integrating and retaining only the linear terms in h and l. By retaining the quadratic terms in h and l, Bhatnagar and Taqvi [8] generated the short periodic expressions: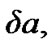
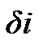

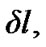
 and
and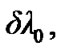 where
where , to an accuracy of second-order in eccentricity.
, to an accuracy of second-order in eccentricity.
In this Paper, an analytical theory for calculating the perturbations due to J2 in the orbital elements of a satellite to accuracy up to fourth power in eccentricity is derived. The mean orbital elements, particularly semimajor axis and eccentricity generated using first-order theory (only linear terms in e) and second-order theory (linear and quadratic terms in e) are compared with those computed using developed fourth-order theory. It is observed that there is significant improvement in the important orbital elements: semi-major axis, eccentricity and inclination with the present theory over the secondorder theory of Bhatnagar and Taqvi.
2. Perturbations Due to J2
If the Earth is assumed to be an oblate spheroid and only J2 term in the oblateness is considered, then the disturbing function is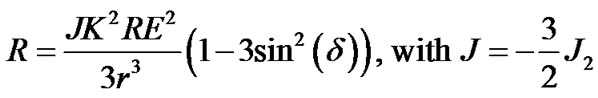 where
where  km3/s2 is the Gaussian constant, r is the radial distance of the satellite, RE = 6378.15 km, is the equatorial radius of the Earth, δ the declination of the satellite, and
km3/s2 is the Gaussian constant, r is the radial distance of the satellite, RE = 6378.15 km, is the equatorial radius of the Earth, δ the declination of the satellite, and 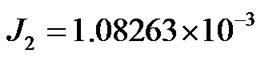 is the second harmonics of the Earth.
is the second harmonics of the Earth.
To expand R in powers of eccentricity of the satellite orbit, utilizing the relation where
where 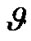 is the true anomaly, using this in R, we obtain
is the true anomaly, using this in R, we obtain
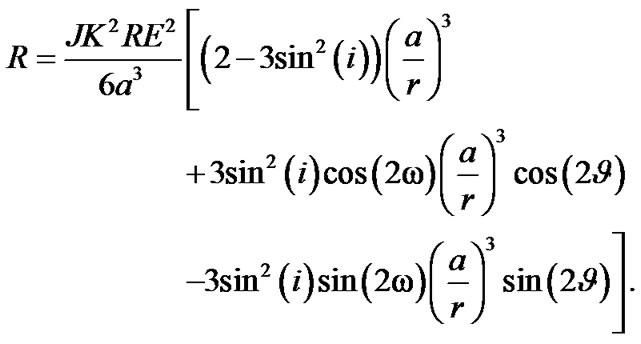
The quantities 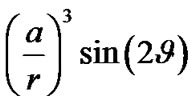
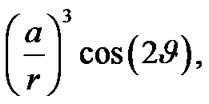

can be expanded in series in terms of multiples of the mean anomaly M.
Considering the terms up to sixth order in eccentricity with the help of “MAXIMA” software available in public domain [12], we obtain an expression for the disturbing function in the form

The coefficients  depend on the variables a, e, and i.
depend on the variables a, e, and i.
The transformation of the disturbing function R into the new variables h, l and λ can be carried out with the aid of the following relations
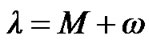
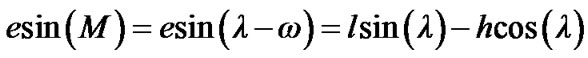


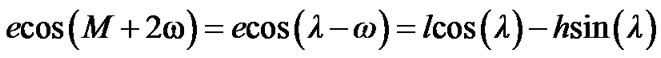
The disturbing function R will then be a function of l, h and .
.
By introducing the variables ,
,  , the Lagrange’s planetary equations of motion can be expressed as
, the Lagrange’s planetary equations of motion can be expressed as
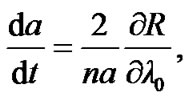

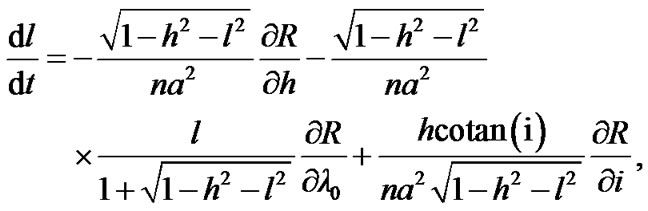
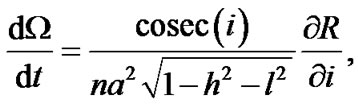


where 
Computing the derivatives of the disturbing function with the help of MAXIMA and introducing the results in the above equations of motion and integration leads to the expressions given in Appendix. They define the first-order perturbations of the orbital elements of the satellite with the fourth-order accuracy in the eccentricity. The perturbations of the orbital elements are now found from the relations
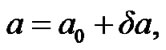
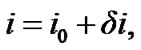

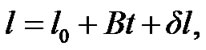
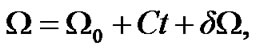

where A, B, C, D are four constant coefficients of the secular perturbations.  and
and  contain only periodic terms.
contain only periodic terms.  and
and  are six constants of integration.
are six constants of integration.
Writing

For the mean elements of the orbit at time t, we have for the perturbed elements
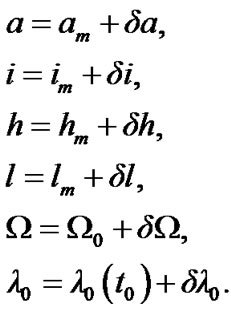
The elements a, e, h, l, 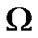 and
and 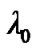 are called the osculating elements of the orbit at time t. We utilize the uniformly regular KS canonical equations of motion provided in [13] for generating the osculating orbital elements with Earth’s zonal harmonics terms J2 to J6 with the detailed procedure provided in Sharma and Raj [14]. The mean orbital elements are then computed by using the iterative scheme of Gooding [11].
are called the osculating elements of the orbit at time t. We utilize the uniformly regular KS canonical equations of motion provided in [13] for generating the osculating orbital elements with Earth’s zonal harmonics terms J2 to J6 with the detailed procedure provided in Sharma and Raj [14]. The mean orbital elements are then computed by using the iterative scheme of Gooding [11].
3. Results
To compare the developed fourth-order theory with the first-order and the second-order theories, various test cases are considered. A study in the variations of the important orbital parameters: semi-major axis, eccentricity and inclination due to the variations in semi-major axis, eccentricity and inclination have been carried out.
Table 1(a) provides the minimum and maximum values of the osculating and mean semi-major axis for different inclinations and eccentricities as well as the difference in maximum and minimum mean semi-major axis with respect to second-order and fourth-order theories during a revolution. The values of other orbital parameters a, Ω, ω and M used in the computation are 8000 km, 60˚, 60˚ and 0˚, respectively. It can be observed that the difference in mean semi-major axis with fourth-order theory is less than that with second-order theory. The maximum and minimum values of difference in mean semi-major as calculated with second-order theory is 16.48 m and 3209.73 m, respectively, while these values as calculated using the fourth-order theory are 4.71 m and 568.04 m, respectively. For both the cases, minimum value correspond to e = 0.05 and i = 5˚ and maximum value corresponds to e = 0.2 and i = 85˚.
Similar observation can be made from the Tables 1(b) and (c), where the difference in the mean eccentricity and the mean inclination is compared for second-order and fourth-order theory for various inclinations and eccentricities. The minimum and maximum values of difference in mean eccentricity calculated from second-order and fourth-order theory is 1.0 × 10–5 and 3.60 × 10–4, 0.98 × 10–5 and 1.69 × 10–4, respectively. The minimum and maximum value of difference in mean inclination calculated from second-order theory and fourthorder theory is 0.23 × 10–4 and 2.08 × 10–3, 0.19 × 10–4 and 2.84 × 10–4, respectively.
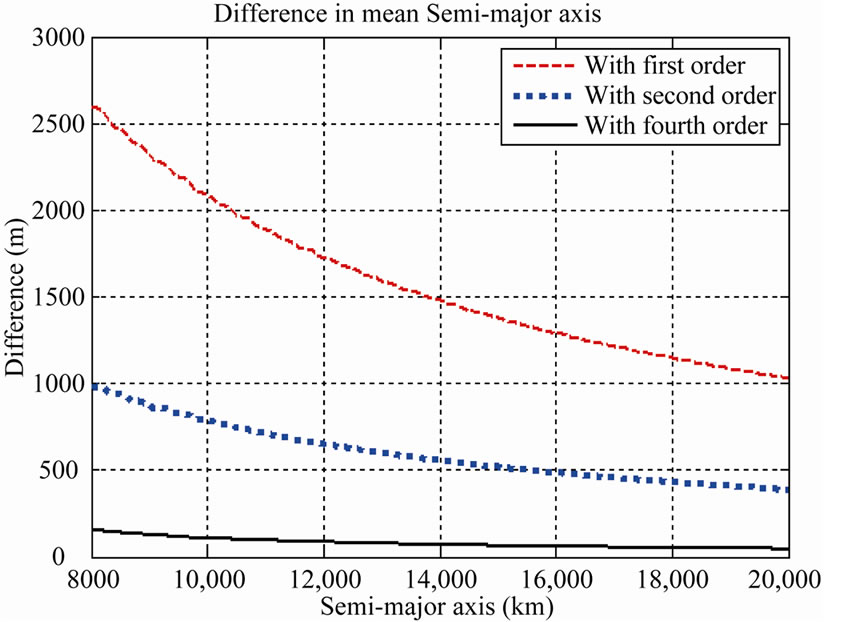
Figure 1(a) shows the difference in maximum and minimum mean semi-major axis during a revolution with respect to different semi-major axis ranging from 8000 km to 20,000 km. The initial values for e, i, Ω, ω and M are 0.2, 30˚, 60˚, 0˚ and 0˚, respectively. The comparisons clearly show that the mean semi-major axis computed using the fourth-order theory is better than that with first-order as well as second-order theory. Similarly, Figure 1(b) gives the difference in maximum and minimum mean eccentricity and Figure 1(c) provides the difference in maximum and minimum mean inclination. Also, it can be observed that the difference in maximum and minimum mean values of semi-major axis, eccentricity and inclination decreases with the increase in the semi-major axis.
In Figures 2(a)-(c), the eccentricity is varied from 0.001 to 0.3 keeping other orbital parameters constant. The initial orbital values for a, i, Ω, ω and M for this case are 10,000 km, 60˚, 60˚, 0˚ and 0˚, respectively. Figure 2(a) shows the difference in maximum and minimum mean semi-major axis computed using firstorder, second-order and fourth-order theories. The difference in maximum and minimum mean eccentricity calculated using first-order, second-order and fourthorder theories is shown in Figure 2(b). Similarly, Figure 2(c) shows the difference in mean inclination. From Figures 2(a)-(c), it is clear that the fourth-order theory is much better than the first-order and the second-order theory. The difference in the maximum and the minimum mean values of semi-major axis, eccentricity and inclination increases with the increase in eccentricity.
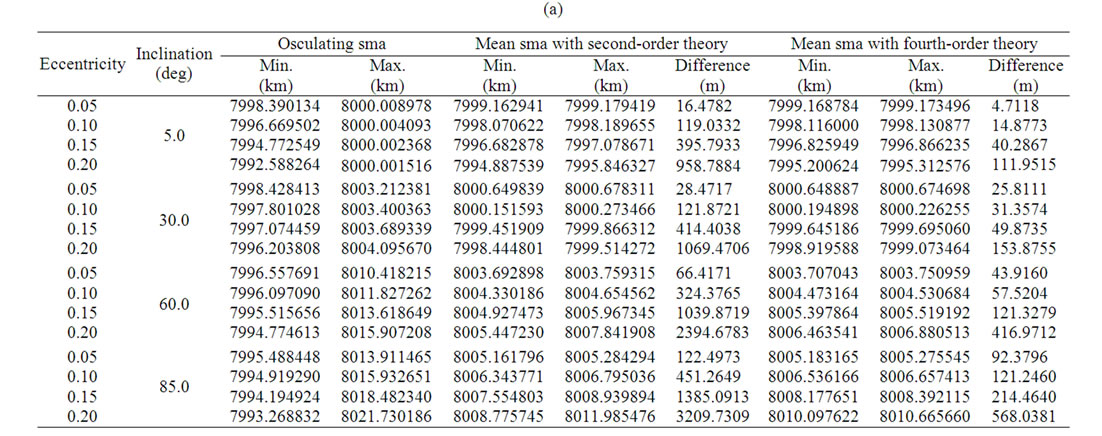


Table 1. (a) Osculating and mean Semi-major Axis (sma) with second-order and fourth-order theory; (b) Osculating and mean Eccentricity with second-order and fourth-order theory; (c) Osculating and mean Inclination with second-order and fourth-order theory.
 (a)
(a)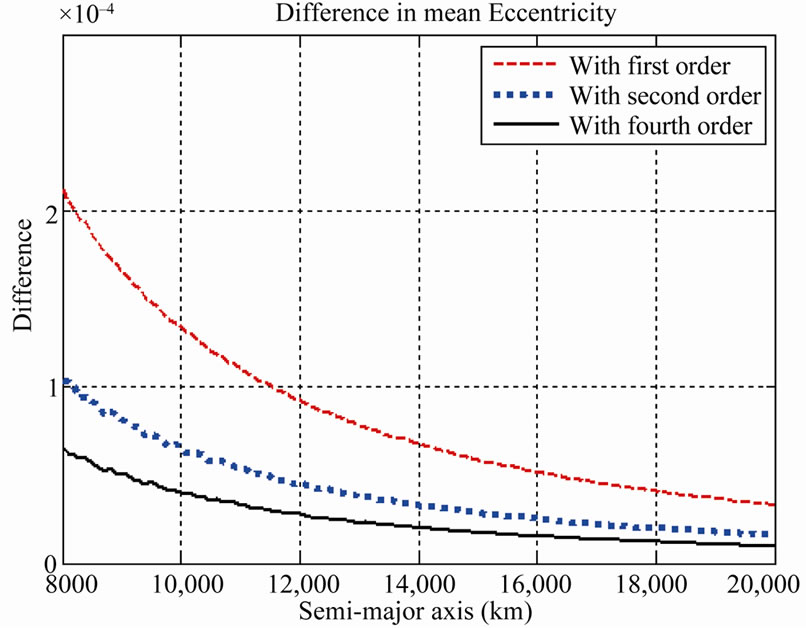 (b)
(b) (c)
(c)
Figure 1. (a) Deviation in mean semi-major axis with variation in semi-major axis; (b) Deviation in mean eccentricity with variation in semi-major axis; (c) Deviation in mean inclination with variation in semi-major axis.
 (a)
(a) (b)
(b) (c)
(c)
Figure 2. (a) Deviation in mean semi-major axis with variation in eccentricity; (b) Deviation in mean eccentricity with variation in eccentricity; (c) Deviation in mean inclination with variation in eccentricity.
The difference of mean semi-major axis, mean eccentricity and mean inclination over a revolution computed using first-order, second-order and fourth-order theories with inclination varying from 0˚ to 90˚ is plotted in Figures 3(a) and 3(b), respectively. The initial values for a, e, Ω, ω and M for this case are 8000 km, 0.2, 60˚, 0˚, respectively. It can be observed that the fourth-order theory developed in this paper is better than the first and the second-order theory. The difference in maximum and minimum mean values of semi-major axis and eccentricity increases with inclination, while the difference in mean inclination first increases, attains a maximum value and then decreases.
4. Conclusions
An analytical theory for calculating first-order perturbations of the orbital elements of a satellite to accuracy up to fourth power in eccentricity is derived. The developed fourth-order theory is compared with first-order theory and second-order theory for different values of semimajor axis, eccentricity and inclination. It is observed that there is significant improvement in the important orbital elements: semi-major axis, eccentricity and inclination with the present theory. The theory provides better estimates of the mean orbital elements up to first-order terms of oblateness of Earth.
 (a)
(a) (b)
(b)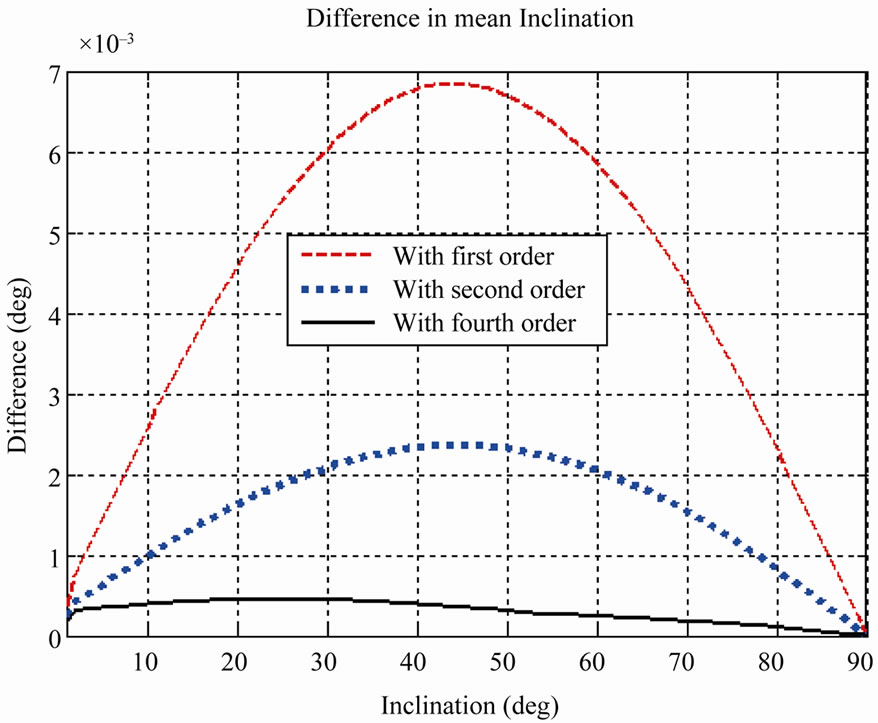 (c)
(c)
Figure 3. (a) Deviation in mean semi-major axis with variation in inclination; (b) Deviation in mean eccentricity with variation in inclination; (c) Deviation in mean inclination with variation in inclination.
5. References
[1] Y. Kozai, “The Motion of a Close Earth Satellite,” Astronomical Journal, Vol. 64, 1959, pp. 367-377.
[2] D. Brouwer, “Solution of the Problem of Artificial Satellite Theory without Drag,” Astronomical Journal, Vol. 64, 1959, pp. 378-396. doi:10.1086/107958
[3] G. A. Chebotarev, “Motion of an Artificial Satellite in an Orbit of Small Eccentricity,” AIAA Journal, Vol. 2, No. 1, 1964, pp. 203-208.
[4] A. Deprit and A. Rom, “The Main Problem of Satellite Theory for Small Eccentricities,” Celestial Mechanics, Vol. 2, No. 4, 1970, pp. 166-206.
[5] K. Aksnes, “A Second-Order Artificial Satellite Theory Based on an Intermediate Orbit,” The Astronomical Journal, Vol. 75, No. 9, 1970, pp. 1066-1076. doi:10.1086/111061
[6] J. J. F. Liu, “Satellite Motion about an Oblate Earth,” AIAA Journal, Vol. 12, No. 11, 1974, pp. 1511-1516.
[7] H. Kinoshita, “Third-Order Solution of an Artificial Satellite Theory,” SAO Special Report #379, 1977.
[8] K. B. Bhatnagar and Z. A. Taqvi, “Perturbations of the Elements of Near-Circular Earth Satellite Orbits,” Proceedings of the Indian National Science Academy, Vol. 43, No. 6, 1977, pp. 432-451.
[9] R. H. Gooding, “A Second-Order Satellite Orbit Theory, with Compact Results in Cylindrical Coordinates,” Philosophical Transactions of the Royal Society, Vol. 299, No. 1451, 1981, pp. 425-474.
[10] R. K. Sharma, “On Mean Orbital Elements Computation for Near-Earth Orbits,” Indian Journal of Pure and Applied Mathematics, Vol. 21, No. 5, 1990, pp. 468-474.
[11] R. H. Gooding, “On the Generation of Satellite Position (and Velocity) by a Mixed Analytical-Numerical Procedure,” Advances in Space Research, Vol. 1, No. 6, 1981, pp. 83-93. doi:10.1016/0273-1177(81)90010-7
[12] Macsyma, Inc., “Mascsyma User’s Guide,” Macsyma, Inc., Boston, 1992
[13] E. L. Stiefel and G. Scheifele, “Linear and Regular Celestial Mechanics,” Springer-Verlag, Berlin, 1971.
[14] R. K. Sharma and M. X. J. Raj, “Long Term Orbit Computations with KS Uniformly Regular Canonical Elements with Oblateness,” Earth, Moon and Planets, Vol. 42, No. 2, 1988, pp. 163-178. doi:10.1007/BF00054544
Appendix