Journal of Sensor Technology Vol.05 No.01(2015), Article ID:54245,12
pages
10.4236/jst.2015.51003
Start-Up Acceleration of Quartz Crystal Oscillator Using Active Inductance Double Resonance and Embedded Triggering Circuit
Tomio Sato1, Akira Kudo2, Tetsuya Akitsu1*
1 Department of Human, Environment and Medical Engineering, Interdisciplinary Graduate School of Medicine and Engineering, University of Yamanashi, Kofu, Japan
2SEIKO EPSON Corporation, Suwa, Japan
Email: *akitsu@yamanashi.ac.jp
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 3 February 2015; accepted 20 February 2015; published 26 February 2015
ABSTRACT
Low-frequency double-resonance quartz crystal oscillator was developed with active inductance circuit aiming the start-up of stable oscillation of tuning fork-type quartz crystal resonator at 32.768 kHz within 0.37 ms. The initial oscillation is triggered by a part of crystal oscillator forming a CR oscillator. The negative resistance ranges to 4 MΩ at gmf of 4.1 μA/V. In a limited frequency range, the circuit shows negative reactance Ccci = −3.4 pF equivalent to inductance Lcc = 9.8 H. The Allan standard deviation indicated 10−11 to 10−10, showing high stability comparable to general quartz crystal oscillator.
Keywords:
Double Resonance Quartz Crystal Oscillator, Active Inductance

1. Introduction
Piezoelectric quartz crystal oscillators have widely expanded in sensing of the environmental data such as static pressure and temperature. Acceleration of the piezoelectric oscillator enables the intermittent operation of the piezoelectric sensor for power management. Engineering issue in the acceleration of the start-up of low frequency quartz crystal oscillator includes 1) triggering circuit, 2) generation of large negative resistance, and 3) linearity of the active device in large amplitude oscillation. In this work, we aim at the acceleration of the start- up of low frequency, tuning fork quartz crystal resonator within several oscillation periods, which enables the intermittent operation of the sensor system. Acceleration of the start-up is studied by the gain control in the quartz crystal oscillator using a cascade circuit in the frequency region of several Mega Hertz [1] -[3] . In recent works, double-resonance quartz crystal oscillator was reported for the enhancement of the frequency pulling [4] and the mode separation of the multimode quartz crystal resonator [5] . Stability of the oscillation frequency is generally discussed based on the moving average of the variance determined for the discrete samples following the proto call [6] -[8] . The modified Allan standard deviation for moving average of finite length data (k = 10) was employed as the measuring rule of the short range stability.
2. Design and Analysis of Quartz Crystal Oscillator
2.1. Acceleration of the Start-Up of a Quartz Crystal Oscillator
Figure 1 shows a circuit diagram of the active inductance double resonance oscillator circuit. The initial oscillation is generated by a part this oscillator acting as a CR oscillator, and after the oscillation of the quartz crystal resonator current starts, the double resonance is established between the quartz crystal and an active inductance combined with the parallel capacitance resulting in the generation of negative resistance. Essential circuit constants R2, C4, and C0 satisfy this resonance condition, where C0 is the parallel capacitance of the quartz crystal resonator. R2 settles the bias in the initial stage of the oscillation. C4 stores the ground potential at the activation of the Vcc voltage, inserted between the node connecting two inverters. The oscillation frequency is determined by a recharging-time constant R2 multiplied by C4. Capacitors C2 and C3 are load capacitors which is necessary for the generation of negative resistance. C5 and C6 are pass-capacitors between the bus-line and the circuit ground. C0 and C1 are reserved for the parallel capacitance of the resonator and the series capacitor of the motion arm. The maximum negative resistance is generated at specified value of the conductance gmf of the active circuits: CMOS (Complementary Metal Oxide Semiconductor) inverters IC1 and IC2. The conductance is controlled by negative feedback resistors Rf = R3, R4, R5, and R6.
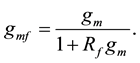 (1)
(1)
Figure 2 shows simplified equivalent circuit-1. CMOS inverter IC1 and IC2 is replaced by two current sources controlled by the gate voltage Vin and Vg.
Applying Kirchhoff’s law, the relations for Iout and Vin are found. Vin is the input voltage of IC1 and Iout is the output current of IC2.
Figure 1. Circuit diagram of the quartz crystal oscillator. Circuit constants: Bias resistors R3, R4, R5 and R6 = 3.3 kΩ, feedback resistor R2 = 3 MΩ, varied for the optimum setting ; C2, C3, and C4 = 10 pF; C5 = 0.1 μF; C6 = 10 μF; C7 = 100 pF; Inverter IC1 and IC2 TC7SHU04F; Vcc= 3 V. Equivalent circuit constant of the quartz crystal resonator: f1 = 32.768 kHz; L1 = 11,797 H; R1 = 47.6 kΩ; C1 = 2fF.
Figure 2. Simplified circuit: equivalent circuit-1.
 (2)
(2)
 (3)
(3)
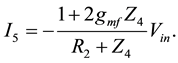 (4)
(4)
 (5)
(5)
Solving for the relation between Iout and Vin, total conductance GM is found.
 (6)
(6)
Then the following relation is found. Current I2, I3 are expressed in the terms of I1.
 (7)
(7)
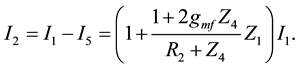 (8)
(8)
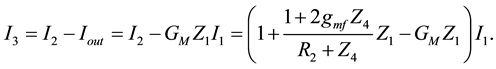 (9)
(9)
Rearranging the expression, relation (11) is found.
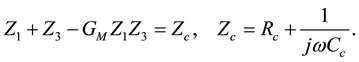 (10)
(10)
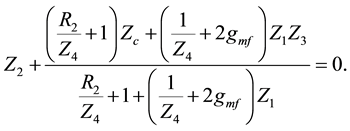 (11)
(11)
Z2 is the impedance of a quartz crystal resonator (Zxt), and impedance for other components is defined as in (12). The composed impedance Zcc of the active circuit is found, substituting the impedance. From the condition for the non-zero solution of current, the oscillation condition results in (13). The impedance of the circuit is divided into resistive and reactance parts.
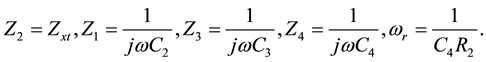 (12)
(12)
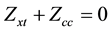 (13)
(13)
 (14)
(14)
The equivalent resistance and the reactance of the circuit are found. Equivalent inductance Lcc or capacitance Ccc is determined depending on sign of reactance Xcc.

Factors “a”, “b”, “c” and “d” are introduced for the simplicity of the expression, where factors “c” and “d” have the dimension of Ω and factors “a” and “b” are dimensionless numbers.
GM is separated into real and imaginary parts.


Introducing (13) and (19) into Zcc, the impedance of the active circuit is found.

Figure 3 shows simplified diagram of equivalent circuit-2 of the oscillator.
The active circuit is indicated with Rcc and reactance Ccc or Lcc depending on the sign. The resonator consists of parallel capacitance C0 and the motion arm, L1, C1, and R1, the equivalent series inductor, capacitor, and resistor respectively. CS is a stray capacitance. Calculating the parallel composition of C0 and Cs with the active circuit, equivalent circuit-3 in Figure 4 is found. Composed equivalent resistance Rcci and capacitance Ccci are found.

Negatively signed capacitance is converted to an active inductance by relation (21),

Figure 3. Equivalent circuit-2.
Figure 4. Equivalent circuit-3.
The denominator of negative resistance Rcci has quadratic dependence on Rcc. The maximum value of the absolute value is reached at a specific value of Rcc determined by C0s and Ccc. The following relation is fulfilled.

The active inductance appears in the vicinity of the resonance frequency, while capacitance Ccc is negative. The resonance frequency is determined by Lcc, C0s, and the sum of C0 and Cs. In this simplified form, the absolute value of negative resistance Rcci becomes infinitely large, if Ccc approaches-C0s and condition (23) is fulfilled.

At the resonance frequency determined by Lcc and C0s, the absolute value of negative resistance determines the growth of signal. The suppression of negative resistance by inductance L1 establishes the stability and inhibitory action against the signal growth. Table 1 shows the equivalent circuit constant of the quartz crystal resonator.
Figure 5 compares the absolute value of negative resistance Rcci for parameters Lcc and Ccc. Figure 6 shows the absolute value of negative resistance Rcc as functions of frequency and gmf. The enhancement of negative resistance and the correlation with active inductance is explained in the following part. Resonance occurs in the inductive region of the motion arm, while the reactance of the active circuit is capacitive. The maximum absolute value of negative resistance approximately 1.3 MΩ is obtained with infinitely large Ccc. The maximum value is limited at 0.8 MΩ for Ccc = 5 pF, a practical value. Larger negative resistance is generated in the region where the active circuit is inductive. When the circuit reactance is inductive, the maximum value increases. The maximum absolute value of negative resistance approximately 13 MΩ for Ccci = −2 pF equivalent to active
Table 1. Equivalent circuit constant of the quartz resonator.
Figure 5. Comparison of the absolute values of negative resistance for Lcc and Ccc, as functions of the negative resistance Rcc. Circuit constants: C0 = 1.14 pF; CS = 1 pF.
Figure 6. Absolute value of negative resistance Rcc and reactance Ccc as functions of frequency and gain. Circuit constant: C2 and C3 = 14 pF; C4 = 18 pF; R2 = 1.0 MΩ, (a) gmf = 4 μA/V, (b) fr = 32.768 kHz.
inductance Lcx = 12 H.
In Figure 6(a), parameter gmf is selected at 4 μA/V. At the lower gain, gmf = 2 μA/V, the active inductance appears in the lower frequency region and disappears in the higher frequency region. For example, it appears at 10 kHz and disappears at 27 kHz. The frequency limit is 55 kHz for gmf = 4 μA/V, and 110 kHz for gmf = 8 μA/V. In the lower frequency region, at approximately 9 kHz, the active inductance disappears. Figure 6(b) shows the dependence on conductance gmf. At frequency of 32.768 kHz, the active inductance appears for gmf = 2.4 μA/V. The limit varies depending on the oscillation frequency. The frequency limit is 20 kHz for gmf = 1.5 μA/V, 40 kHz for gmf = 3 μA/V and 110 kHz for gmf =8 μA/V. The negative resistance and the active inductance appear from the low frequency side, and the resonance condition with CR oscillation is established before the motion arm appears.

Figure 7 shows the dependence of the absolute value of negative resistance Rcci on frequency and gmf. Figure 7(a) shows the frequency dependence of Rcci and reactance Lcci, Ccci. The maximum value of negative resistance Rcci ranges to 4 MΩ. This result is obtained in the case of inductive reactance Lcci = 9.8 H. The composed reactance is capacitive Ccci = 3.4 pF. Figure 7(b) shows the dependence of the absolute value of negative resistance Rcci and reactance Ccci on gmf. For gmf = 4.1 μA/V, the absolute value of negative resistance is 4 MΩ. The composed circuit reactance Ccci = −3.4 pF is equivalent to Lcc = 9.8 H.
Figure 8 shows the absolute value of negative resistance for different resonance frequency. This result tells that the active inductance is generated with certain value of gain in a narrow range corresponding to the required frequency. This result indicates that high gain is not necessarily for better performance.
This result suggests a design principle of the circuit: Higher resonance frequency needs higher gmf. In this analysis, we take a look at the circuit impedance from the resonator terminal. The parallel capacitance C0 and stray capacitance Cs are included in the impedance of the active circuit. Thus, the relation between Rcci and Rcc is presented, As a part of the final solution, the result that Rcci becomes infinitely large at Ccc = −C0s, must be interpreted carefully in the context of the actual circuit design. The minimum idea given here is that the active inductance can generate large negative resistance compared to the capacitive region. Actually, Rcc is determined by number of circuit constants and angular frequency of the oscillation, and the strength of the oscillation is limited within the linear region of the active circuit.
2.2. Modelling of the Start-Up of Initial Oscillation
The crystal current through the motion arm is not generated in the initial stage of the oscillation. In another
Figure 7. Absolute value of negative resistance Rcci and reactance as functions of frequency and gmf. Ciruit constant: R2 = 1.9 MΩ; C2 and C3 = 14 pF; C0 = 1.14 pF; C4 = 18 pF; Cs = 1 pF. (a) gmf = 4 μA/V; Cx infinite. (b) fr = 32.768 kHz.
Figure 8. Comparison of negative resistance for different values of gmf and fr. (a) Frequency fr = 20, 32.768, and 40 kHz. Circuit constants: C2 and C3 = 14 pF; C4 = 18 pF; R2 = 1.9 MΩ. (b) gm = 2, 4, and 8 μA/V. Circuit constants: C2 and C3 = 10 pF; C4 = 18 pF. R2 = 1.9 MΩ.
expression, this branch does not exists in the circuit. Because of high Q, the start-up needs reasonable acceleration system. Figure 9 shows simplified circuit diagrams of the oscillation Mode-1 and Mode-2. Before the establishment of the resonance oscillation, parallel capacitance C0 is the existing circuit component and the motion arm is disconnected. Based on the result of analysis, the active circuit is indicated with Ccci and the composed equivalent negative resistance Rcci. The oscillation frequency is determined by the equivalent reactance of the active circuit and C0. The motion arm appears after the certain growth of the crystal current. This figure also explains the relation between Rcc and Rcci. The circuit in Figure 9(b) is closed with the motion arm, and oscillation current i(t) is excited in the closed loop. Vx and Vc may have different initial values, frequency and polarity depending on the switching sequence.
The start-up mode of the oscillator depends on the rise of Vcc. When the bias current increases the CR oscillation as in Mode-1 starts before the establishment of the crystal current. The oscillation frequency of Mode-1 is determined by R2 multiplied by the composed capacitance. When the quartz crystal resonator is activated sufficiently, the motion arm appears in the circuit, as in Model-2. Computer simulation was carried out using LT- spice for Windows (Linear Technology Corporation, 1630 McCarthy Blvd., Milpitas, CA, USA) [9] . Figure 10 shows the transient excitation of the crystal current with matched frequency setting: the oscillation frequency of the CR oscillator is slightly higher than the resonance frequency. The crystal current in the motion arm grows up faster and the oscillation frequency of the entire oscillator circuit is locked to the resonance frequency.
Figure 9. Equivalent circuit diagram of quartz crystal oscillator. (a) Model-1; (b) Model-2.
Figure 10. Initial stage with frequency match conditions. Upper track: Current I(L1) fowing through the series inductance L1. Lower track: Output voltage.
Figure 11 shows the initial stage of the mismatched case. If the frequency of the CR oscillation is too high, and the oscillation apparently starts at different frequency. The oscillation frequency abruptly locked to the crystal resonance frequency by the growth of the crystal current. The faster growth of crystal resonance occurs with frequency mated pumping by the CR oscillation. The similar result of the matched and mismatched case was observed in the experiment.
Figure 12 shows the circuit diagram for the computer simulation. Here, CMOS inverter IC1 and IC2 are replaced with pairs of complementary MOSFETs (Metal Oxide Semiconductor Field Effect Transistor).
The circuit constants of the motion arm are not corresponding to the values assigned in the analysis and experiment. Also, the delayed connection of the motion arm is not considered in this simulation.
When the motion arm is removed, this circuit forms a CR oscillator. The oscillation frequency is determined by the reactance of the parallel capacitance of the quartz resonator and feedback resistor R2. Figure 13 shows a typical wave form of the CR oscillator and FFT spectral analysis, for the matched frequency peak in the vicinity of the resonance frequency of the motion arm. The CR oscillation peak appears in the vicinity of the quartz resonance frequency.
Figure 11. Comparison of growth of the crystal current and output with a mismatch conditions at R2 = 0.8 MΩ. Upper track: Current I(L1) flowing through the series inductance L1; Lower track: Output voltage.
Figure 12. Equivalent circuit for the computer simulation. Courtesy of LTspice, Linear technology corporation.
Figure 13. Typical example for the waveform of the CR oscillator and the FFT spectral analysis R2 = 3.0 MΩ.
3. Experimental Result and Discussions
The start-up and the stability of the stable oscillation of the double resonance oscillator is experimentally evaluated. The stability of the oscillation frequency is analyzed with 53,230 A universal frequency counter (Agilent Technologies, Santa Clara, Ca, USA) synchronized with external rubidium oscillator with long period stability < 2 × 10−11/month and short period stability < 1 × 10−11/s.
3.1. Start-Up of the Double Resonance Quartz Crystal Oscillator
The proposed quartz oscillator circuit is activated with Vcc and the minimum start-up time marked 0.37 ms, as shown in Figure 14. The start-up time and the CR oscillation frequency are shown as functions of the resistance R2. In the proposed oscillator circuit, the output of inverter IC2 is positively fed back to the input of inverter IC1 through the quartz crystal resonator. Replacing the quartz resonator with a capacitor equivalent to the parallel capacitance C0, the circuit exhibits CR oscillation and this frequency is determined by the time constant: R2 multiplied by C4. In the case of R2 = 2.3 MΩ, the frequency of the CR oscillation fCR is approximately equal to the resonance frequency. The quartz crystal oscillation is triggered by the CR oscillation and the start-up time shows its minimum. The entire oscillator circuit is synchronized after short transient, showing the rapid start demonstrated with typical waveform: the initiation of the oscillation within 0.37 ms, several oscillation cycle. Figure 15 shows a typical example for the accelerated start-up of the quartz crystal oscillator.
3.2. Stability of the Double Resonance Quartz Crystal Oscillator
In this experiment, modified two-sample Allan standard deviation is employed as a measure of the short-time frequency stability. This protocol is defined in (25), following IEEE Standard 1139 [9] . The frequency of oscillator circuit fk is the discrete sample of oscillation frequency. τ is the gate time and n is the sequential number of samples. Dimensionless parameter is defined from frequency deviation normalized by the moving average over 10 sequential samples. Figure 16 shows the modified Allan standard deviation showing the short range stability of the order of 10−10 to 10−11. The quartz crystal oscillator was isolated in a shield box with isolated DC power supply. This result satisfies the industrial requirement for the standard quartz sensor.

Table 2 shows the stability of the quartz crystal oscillation in this experiment. This result shows Allan standard
Figure 14. Experimental comparison of the start-up time and the frequency of the CR oscillation.
Figure 15. Start-up of the double-resonance quartz crystal oscillator. Horizontal scale: 100 μs/div. Vertical scale 200 mV/div. Circuit constants: C2, C3 and C4 = 10 pF. Start-up of the stable oscillation 0.37 ms after the activation of Vcc.
deviation of 10−11 satisfy the requirement for the standard sensing. Probably, for the further improvement of the stability, the improvement of the Q-value of the resonator is necessary.
Figure 16. Short range stability of the double-resonance quartz crystal oscillator.
Table 2. Stability: Averaged Allan standard deviation of the proposed circuit.
4. Conclusion
Environmental sensing awaits solutions to reduce the electric-power, in continuous monitoring. The quick start of quartz crystal oscillators allows excitation of stationary oscillation established after short transient meeting the request for the power management in the environmental sensing such as the pressure and temperature. In this work, we resolved the engineering issues for the rapid start-up: 1) Large negative resistance; 2) Low distortion and linearity; 3) Triggering circuit. The start-up of a low frequency quartz oscillator is triggered with a CR oscillator and transferred to a quartz crystal oscillator. The maximum negative resistance ranges to 4 MΩ at specified gain of the active CMOS inverter circuit gmf = 4.1 μA/V. The composed reactance of the active circuit Ccci shows negative value, −3.4 pF which acts as inductance of 9.8 H and generates large negative resistance. Rapid start-up of the oscillation was established by the energy transfer by the initial CR oscillation of the active circuit and the minimum start-up time was realized. The oscillation condition was examined by the analysis and the start-up in the initial stage was examined by the computer simulation and experiment. The result shows corresponding dependence of the start-up time on circuit parameter R2. The stability performance of the double-re- sonance oscillator showed that short range stability of 10−11 satisfies the industrial requirement for the standard quartz oscillator circuit.
Acknowledgements
The authors acknowledge Ms Ruzaini Izyan binti Ruslan and Mr. Satoshi Goto for their collaboration in the early stage of this experiment. This work was supported in part by JST A-STEP Contract No. AS251Z01794J.
References
- Izumiya, S., Asaki, J. and Adachi, T. (2003) Algebraic Analysis Method of Start-Up Characteristics of Cascade Crystal Oscillator. Electronics and Communications in Japan (Part II: Electronic), 86, 32-43. http://dx.doi.org/10.1002/ecjb.10166
- Ulmer, R.W. (1990) Stat-Up Circuit for Low Power MOS Crystal Oscillator. US Patent 4956618.
- Lu, W., Tse, T. and Chan, W.-C. (2006) Crystal Oscillator Circuit Having a Start-Up Time Reduction Circuit. US Patent 7034628 B1.
- Ehara, K., Tanaka, H., Sato, T. and Kanno, Y. (2006) Development of Inductive Quartz Crystal Oscillator Circuit with CMOS Inverter. Proceedings of IEEE Conference on System, Man and Cybernetics, Taipei, 8-11 October 2006, 1425- 1430.
- Izyan-Ruslan, R., Sato, T. and Akitsu, T. (2012) Voltage Controlled Narrow Band Wide-Variable Range Four Segment Quartz Crystal Oscillator. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, 59, 564-572.
- Barnes, J.A., Chi, A.R., Cutler, L.S., Healey, D.J., Leeson, D.B., McGunigal, T.E., Mullen Jr., J.A., Smith, W.L., Sydnor, R.L., Vessot, R.F.C. and Winkler, G.M.R. (1971) Characterization of Frequency Stability. IEEE Transactions on Instrumentation and Measurement, IM-20, 105-120.
- Allan, D.W. (1966) Statistics of Atomic Frequency Standards. Proceedings of the IEEE, 54, 221-230. http://dx.doi.org/10.1109/PROC.1966.4634
- IEEE Standard 1139.
- Linear Technology Corporation (2014) LTspice for Windows. http://www.linear-tech.co.jp/designtools/software/






















