Journal of Sensor Technology
Vol. 3 No. 1 (2013) , Article ID: 29062 , 8 pages DOI:10.4236/jst.2013.31003
Free Vibration Analysis of Elastic Bodies for Six-Axis Force Sensor
School of Mechanical and Automotive Engineering, Anhui Polytechnic University, Wuhu, China
Email: xdz@ahpu.edu.cn, wangzhihong@ahpu.edu.cn
Received November 11, 2012; revised December 15, 2012; accepted December 29, 2012
Keywords: Free Vibration; 6-AFS; Rectangular Plate; Circular Plate; Rayleigh-Ritz
ABSTRACT
Now the six-axis force sensor (6-AFS) is used widely, and as the core components, mechanical properties of its elastic bodies are significant. With the increase of dynamic loads, studies on dynamic characteristics of the 6-AFS become more and more important. In this paper, the study focuses on the free vibration problem of a novel 6-AFS. The research approach is to decompose the sensor into several separate elastic bodies (four lamellas and upper and lower membranes) and research these elastic bodies respectively. The free vibration of the lamella is studied based on Rayleigh-Ritz method and the separation of variables. The analytical solutions of free vibration of the membranes are deduced according to the nature of Bessel functions. Both the analytical results are simulated with MATLAB. Compared the simulated diagrams with actual situations, they are very close. The mode shapes obtained play a major role in solving the forced vibration of the sensor.
1. Introduction
Scientists commit themselves to improving the level of intelligent robots because they want to obtain an equipment that can work as human beings. In order to have the similar functions as human’s hand, the six-axis wrist force sensor is developed which can measure force components 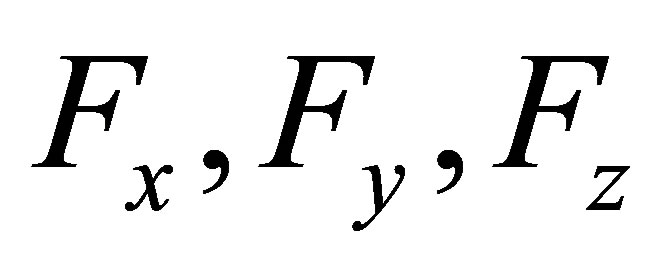 and moment components
and moment components 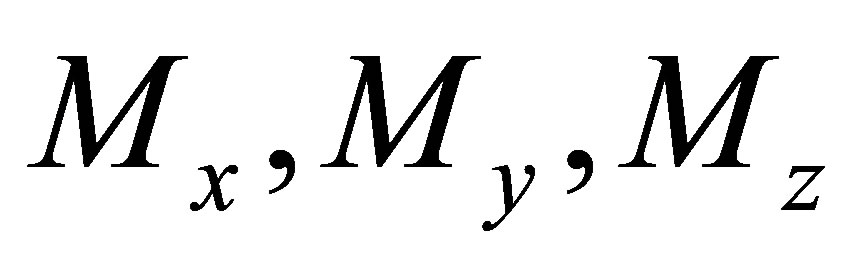 [1,2].
[1,2].
Over the years, static characteristics of multi-axis force sensors have been further studied by domestic and foreign scholars and many achievements have been obtained. In 1990, Tsuneo Yoshikawa, a professor at Kyoto University in Japan, deduced the relationship of stress-strain and static-coupling of a cross-shape force sensor under static load using Material Mechanics in detail [3]. In 2010, K. Q. Liang et al. used Material Mechanics and finite element method to analyze the relationship of stress-strain of a novel 6-AFS at the State Key Laboratory of Sensor Technology, and determined the cross-coupling through static calibration [4]. A. G. Song, a professor at Southeast University, designed a four-axis force sensor with low coupling and analyzed the cross-coupling by using Material Mechanics and finite element method [5]. To improve the accuracy of these force sensors, researchers all over the world have made unremitting efforts. Y. Haddab et al. at French FEMTO-ST Institute used Kalman filtering technique to reduce the output noise [6]. The author of this paper used matrix perturbation theory to discuss the relation between the value of elements in cross-coupling matrix![]() and the sensor’s measuring accuracy. In this paper, an important conclusion was drawn that when the increments of the forces at six directions are the same, the measuring accuracy is ideal, and this conclusion received high attention from researchers at Institute of Intelligent Machines, Chinese Academy of Sciences (CAS) and was seen as one of the bases for the design of multi-axis force sensor (MAFS) [7]. Synthesizing the present research achievements, researches about the static characteristics of MAFS are indepth and sufficient. However, less attention is paid to dynamic characteristics of these sensors. AMTI Inc. is the main manufacturer of MAFS internationally and only the upper limit frequency is given in its instruction. Along with the increase of situations that intelligent robots work under dynamic loads, studies about vibration problem of the MAFS become more and more important. So in this paper, the dynamic problem is researched.
and the sensor’s measuring accuracy. In this paper, an important conclusion was drawn that when the increments of the forces at six directions are the same, the measuring accuracy is ideal, and this conclusion received high attention from researchers at Institute of Intelligent Machines, Chinese Academy of Sciences (CAS) and was seen as one of the bases for the design of multi-axis force sensor (MAFS) [7]. Synthesizing the present research achievements, researches about the static characteristics of MAFS are indepth and sufficient. However, less attention is paid to dynamic characteristics of these sensors. AMTI Inc. is the main manufacturer of MAFS internationally and only the upper limit frequency is given in its instruction. Along with the increase of situations that intelligent robots work under dynamic loads, studies about vibration problem of the MAFS become more and more important. So in this paper, the dynamic problem is researched.
For the mechanical property of a 6-AFS, the focus should be drawn to its sensing elements which are the core components of the sensor. The lightweight thin plate structures have been widely used as elastic bodies to detect the force information, e.g., the four-dimensional fingertip force sensor and the 6-AFS based on double layer E-type membrane developed by Institute of Intelligent Machines, CAS, they all use thin plate as the elastomer to detect the outside force information. Thus, the knowledge of its free vibration is significant to the structural designers [8]. The free vibration characteristic of a elastic thin plate is the basis and has great significance for the follow-up studies of the forced vibration. Since the introduction of the small deflection theory of plate bending, people are interested in vibration problems of the elastic thin plate. The free vibration analysis of rectangular and circular plates is important for the design of plate-type structures. Consequently, a great many of research reports have been conducted on the dynamic behavior of such structures. Leissa offered comprehensive sets of research data for the free vibration of elastic thin plates based on Kirchhoff’s thin plate theory [9]. As closed form solutions for plate vibration problems are known only for certain special cases in which at least a pair of opposite sides is simply supported. One has to use approximate method. As a result, a large number of useful methods have been developed to get solutions for some practical problems. The Rayleigh-Ritz method is one of the most popular methods to obtain the approximate solutions for the natural frequencies of rectangular and annular plates [10-12]. Rayleigh-Ritz method uses a linear combination of some assumed basic functions to express the mode shape. Finite element methods often divide the elastic body into a number of smaller elements and approximate the solution by using local piecewise continuous shape functions [13,14]. And there are some other approximate methods including the differential quadrature (DQ) method [15], the least squares techniques [16], the Meshless methods [17], and the spline finite strip method by G. Akhras and W. Li [18].
In the present paper, Rayleigh-Ritz method and the separation of variables are used to obtain the natural frequencies and the corresponding mode shapes of the Kirchhoff rectangular plate. And according to the nature of Bessel equations and Bessel functions, the analytical expressions of natural frequencies and associated mode shapes of the Kirchhoff circular plate are derived. At last, the simulation diagrams of analytical results are obtained by the software of MATLAB. The natural frequencies and mode shapes deduced will be used to solve the dynamic response of thin plates under harmonic force in follow-up studies.
2. Differential Equation of Thin Plate
2.1. Governing Equations of Rectangular Plate
A vast literature exists about the free vibration of rectangular plates. Consider a thin rectangular plate of length![]() , width
, width 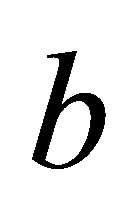 and uniform thickness
and uniform thickness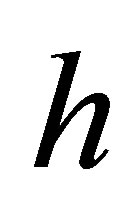 , oriented so that its middle surface contains
, oriented so that its middle surface contains ![]() and
and 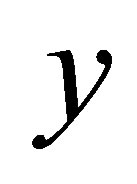 axes of a Cartesian coordinate system (
axes of a Cartesian coordinate system ( ), as shown in Figure 1. Based on Kirchhoff’s thin plate theory, the free vibration differential equation of thin plates is:
), as shown in Figure 1. Based on Kirchhoff’s thin plate theory, the free vibration differential equation of thin plates is:
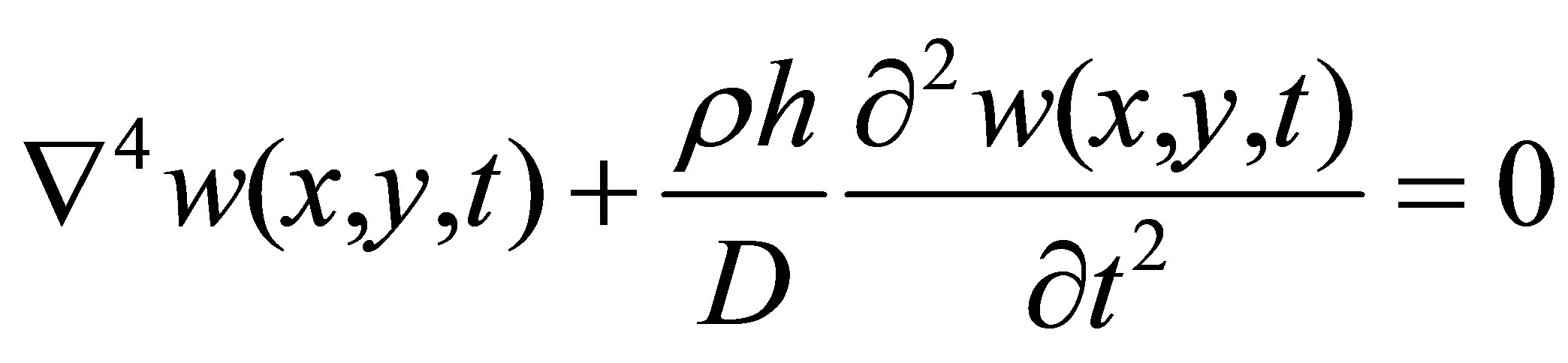 , (1)
, (1)
where ![]() is the transverse deflection;
is the transverse deflection;  is the differential operator in Cartesian coordinates (i.e.,
is the differential operator in Cartesian coordinates (i.e.,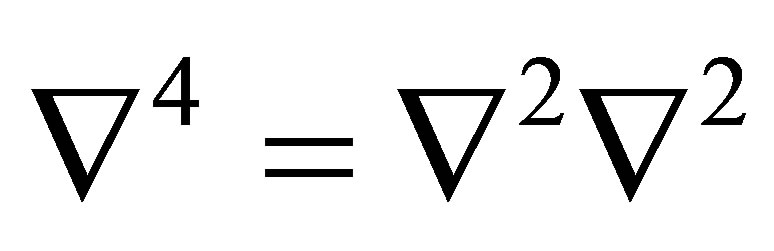 ,
,
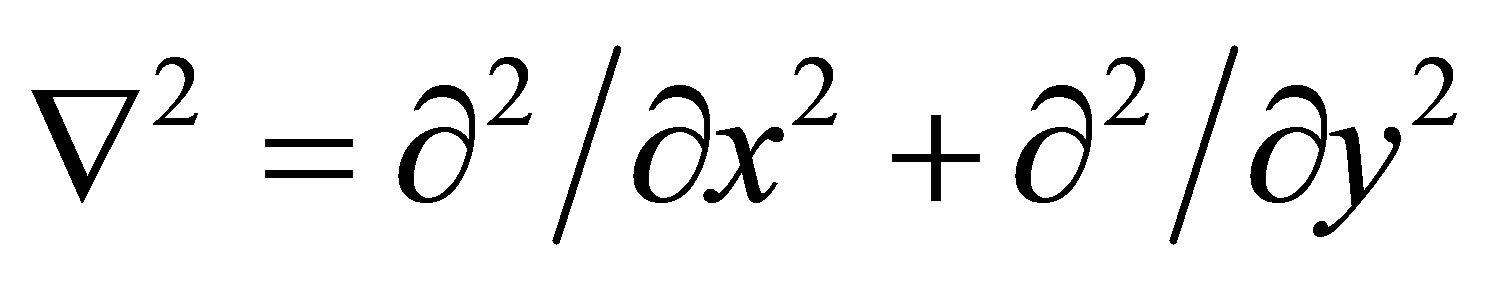 ),
), is the bending rigidity;
is the bending rigidity; 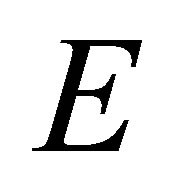 is Young’s modulus;
is Young’s modulus; 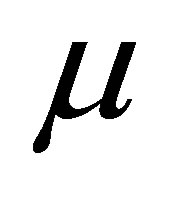 is Poisson’s ratio;
is Poisson’s ratio; 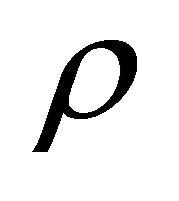 is mass density per unit volume;
is mass density per unit volume; 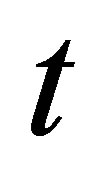 is the time. It is well-known that the free vibration of an elastic linear system is harmonic, therefore, the deflection of free vibration of the thin plate can be assumed to be:
is the time. It is well-known that the free vibration of an elastic linear system is harmonic, therefore, the deflection of free vibration of the thin plate can be assumed to be:
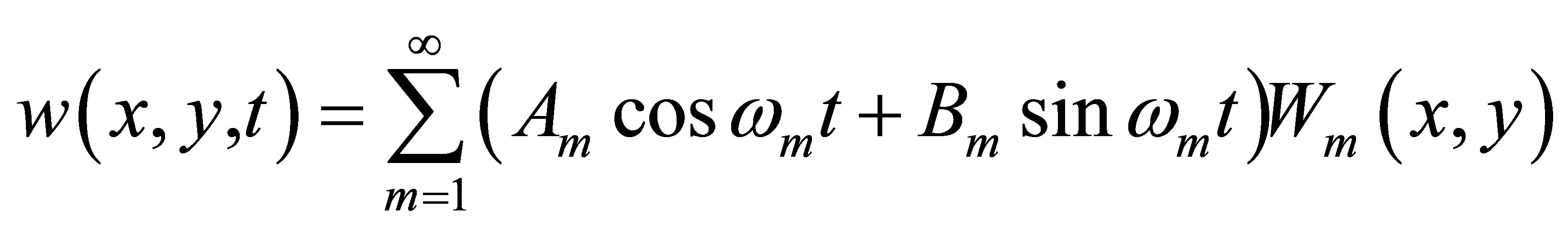 , (2)
, (2)
where 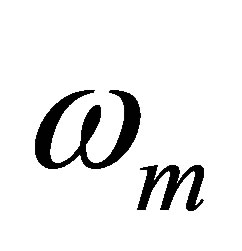 is the natural frequency,
is the natural frequency, 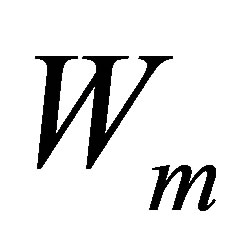 is the associated mode shape,
is the associated mode shape, 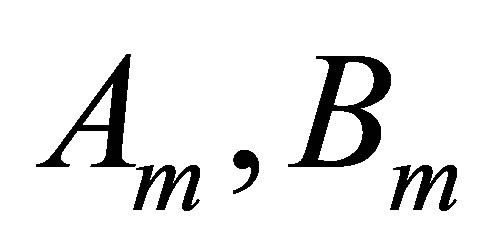 depend on initial conditions. Considering one solution with the general form:
depend on initial conditions. Considering one solution with the general form:
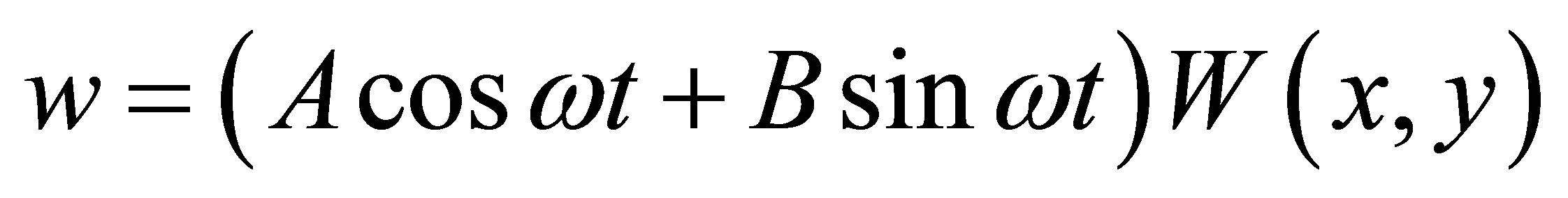 , (3)
, (3)
then it is possible to obtain the following equation in terms of spatial variables only:
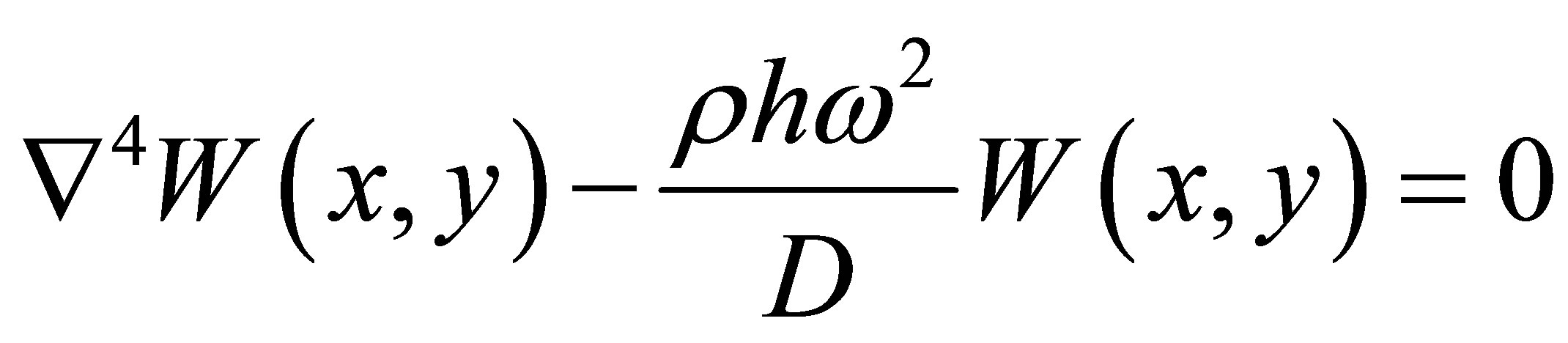 . (4)
. (4)
This equation is a two-dimensional partial differential equation, and the exact solution is limited to vibration problems with simple shape, load and boundary conditions. There are no exact solutions for natural frequencies and associated mode shapes of the transverse vibrations except plates with four edges or one opposite edges simply supported. For the case of complex shape, load or boundary conditions, approximate method must be used, such as lumped mass method, finite element method and assumed mode method. In this paper, Rayleigh-Ritz method is adopted [19].
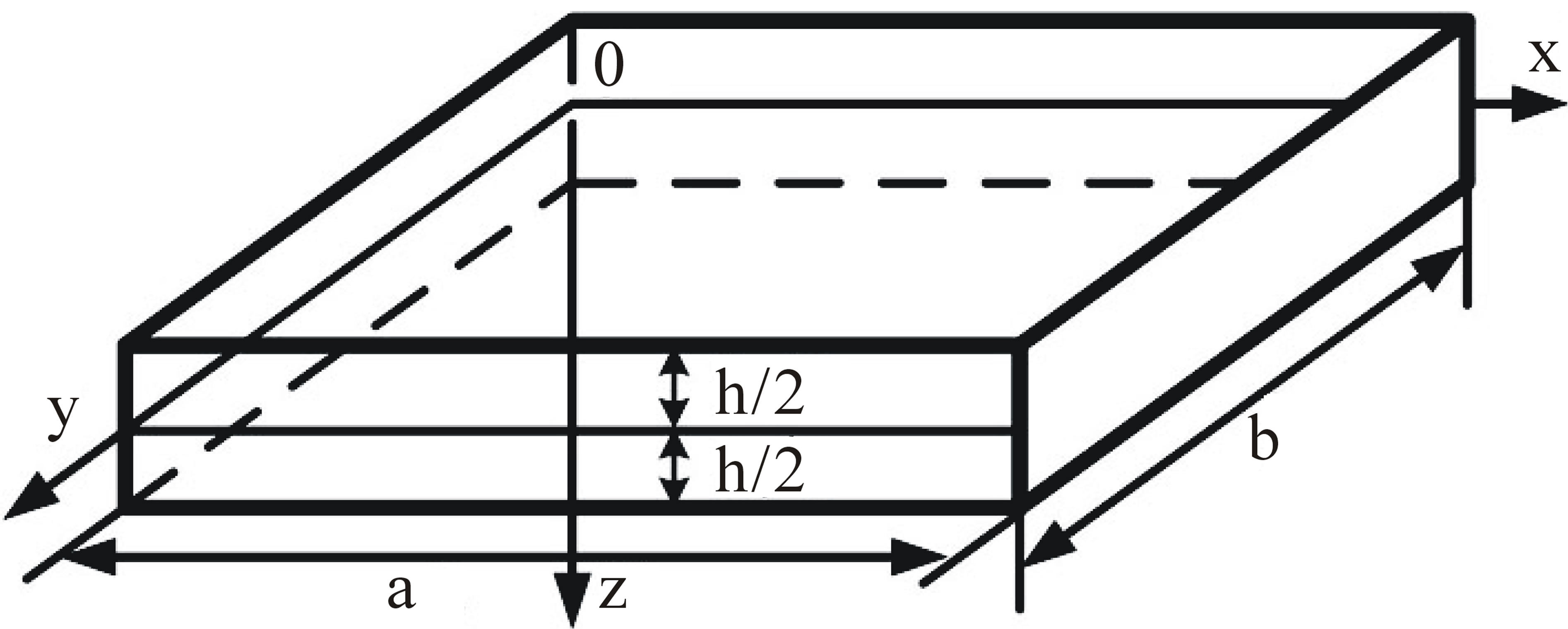
Figure 1. The rectangular plate.
2.2. Rayleigh-Ritz Method Rayleigh-Ritz method is a semi-analytical method and widely used in solving free vibration problems of the thin plate. For this method, the vibration mode shape is expressed in terms of the plate characteristic functions as:
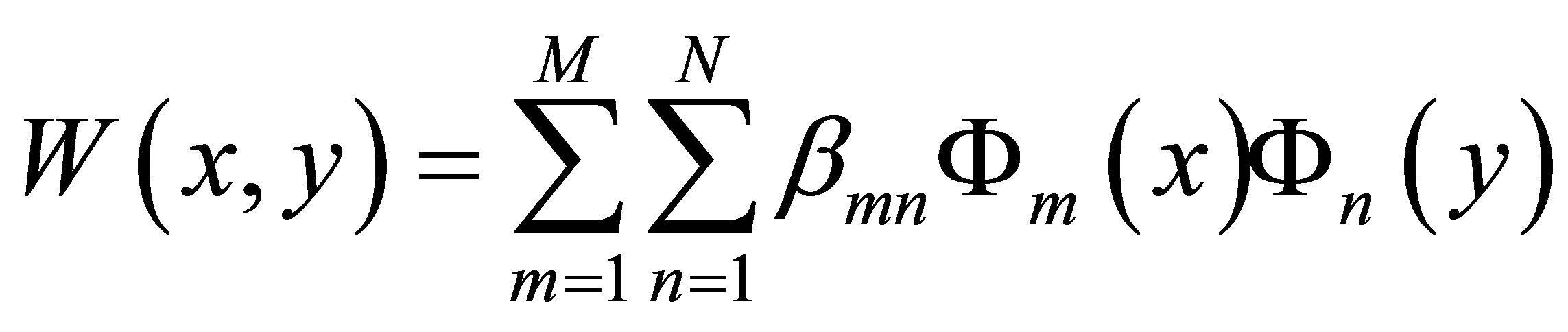 . (5)
. (5)
where 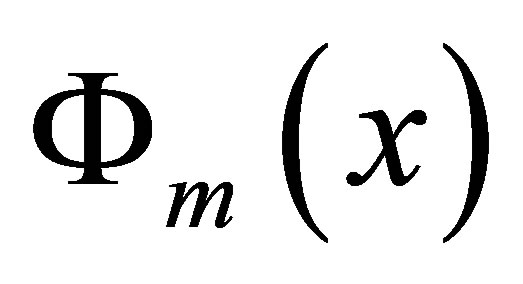 and
and 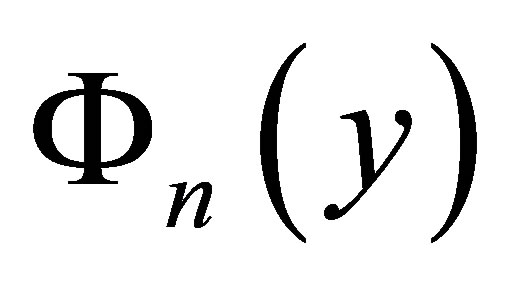 are polynomial functions depending upon the boundary conditions of the plate,
are polynomial functions depending upon the boundary conditions of the plate, 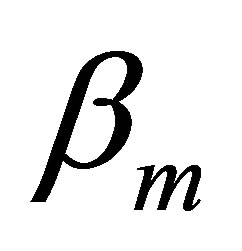 is the unknown parameter that need to be found.
is the unknown parameter that need to be found.
The procedure of free vibration doesn’t involve any outside force, and the expressions for the maximum strain and kinetic energy respectively are:
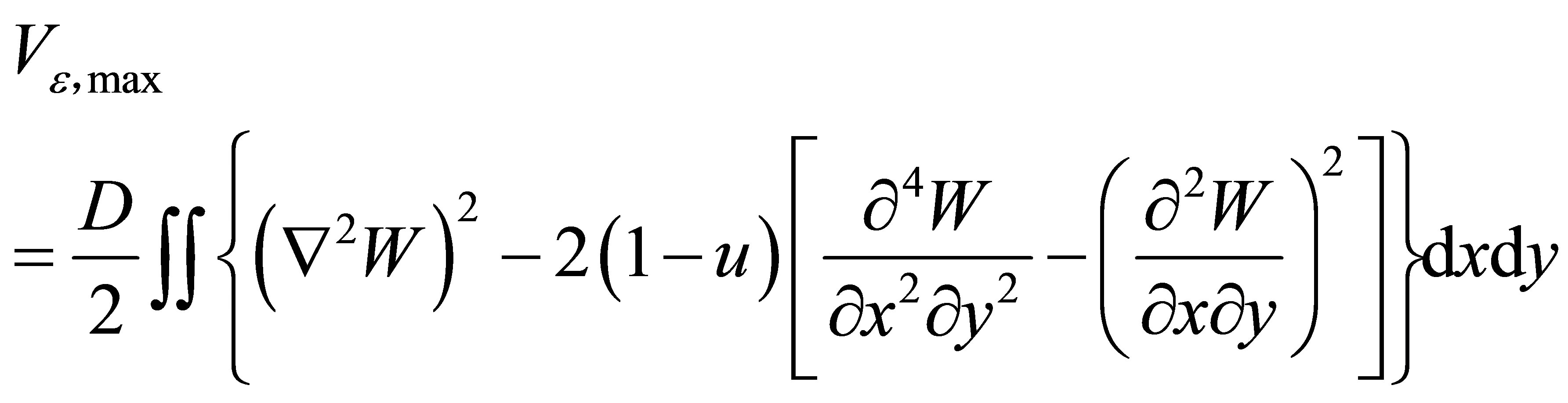 ,(6)
,(6)
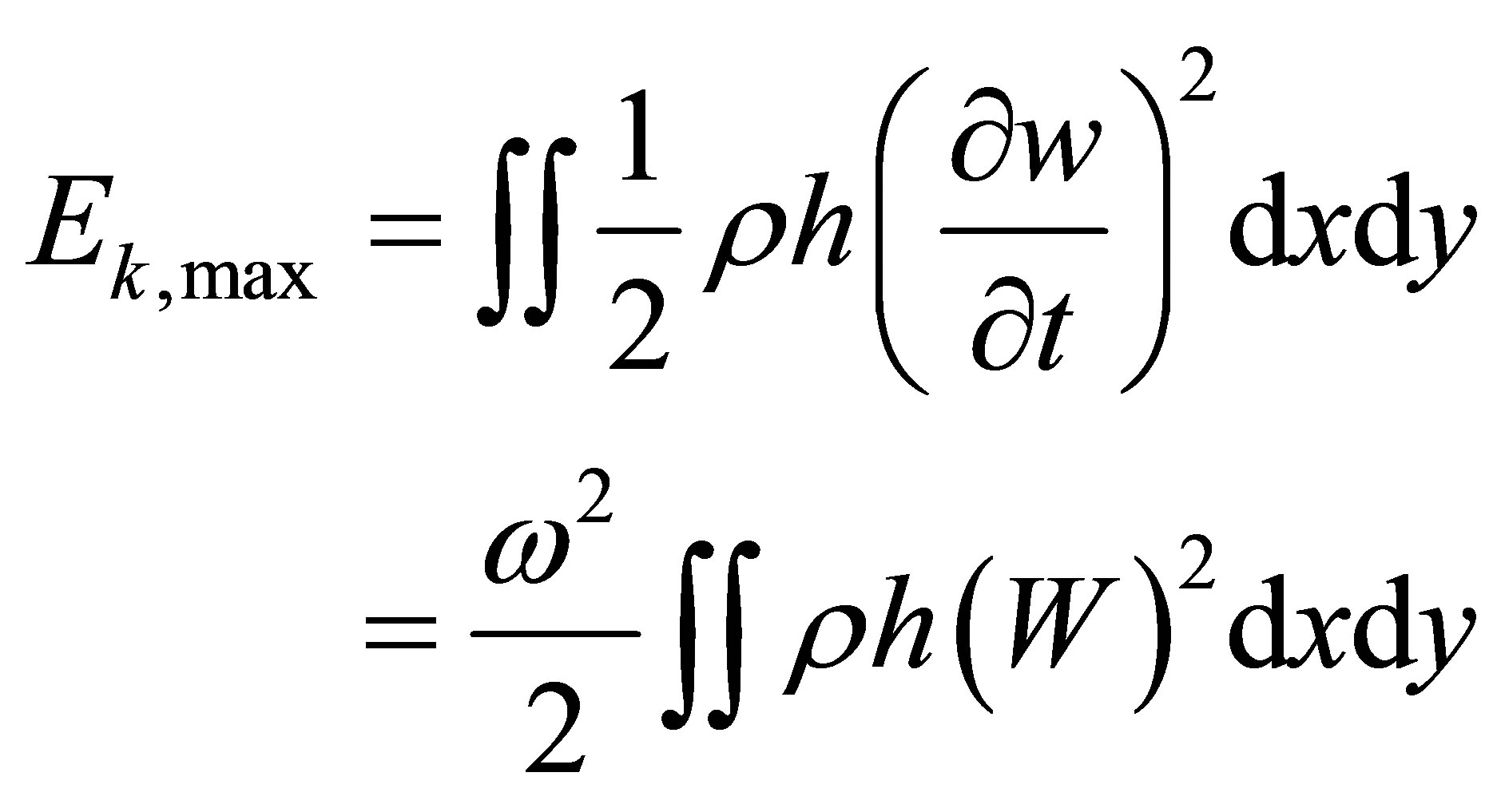 (7)
(7)
The principle of minimum potential energy is that for the constraint of boundary conditions, the potential energy corresponding to the exact solution is less than any other possible potential energy. Then the variation of potential energy functional should be zero, namely,
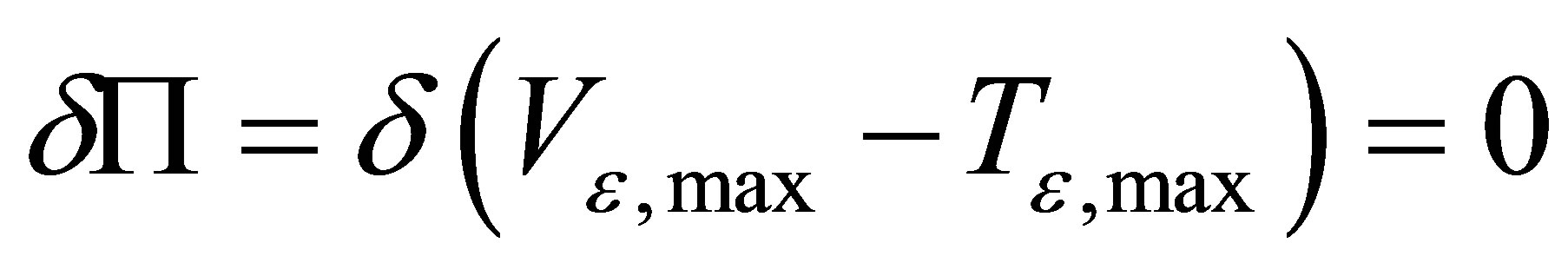 .
.
Minimization of the difference between 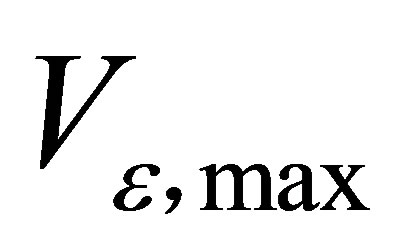 and
and  with respect to each of the coefficient
with respect to each of the coefficient 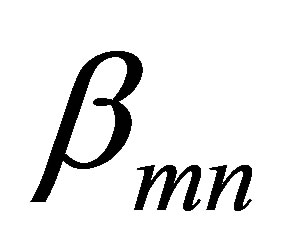 leads to:
leads to:
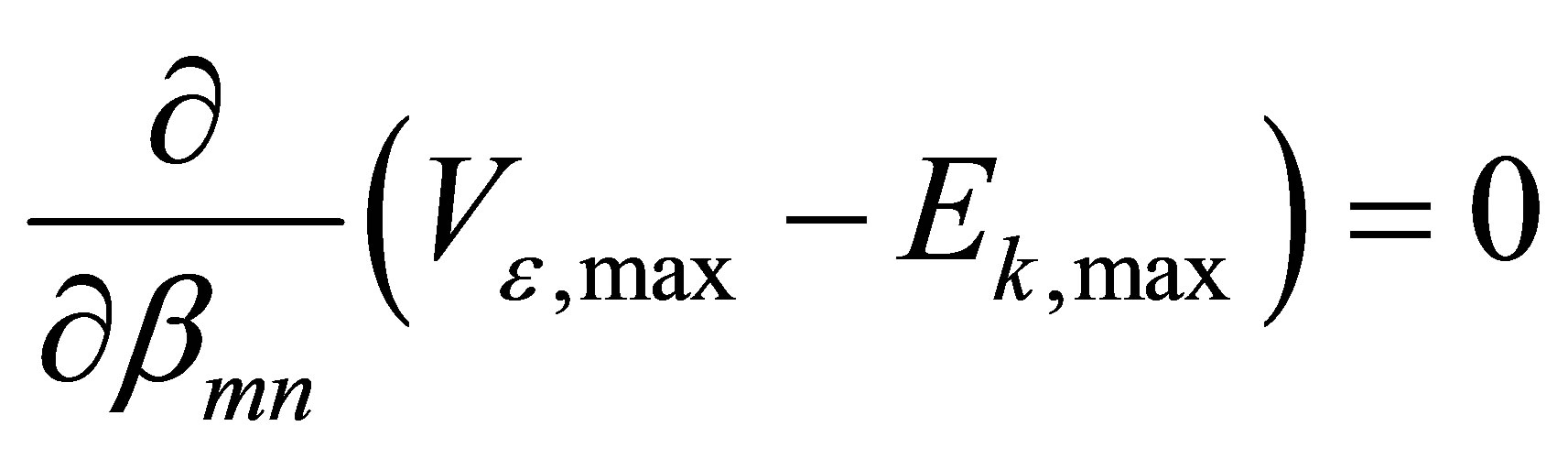 , (8)
, (8)
where 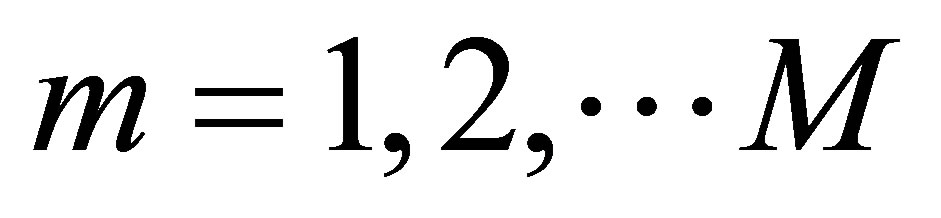 and
and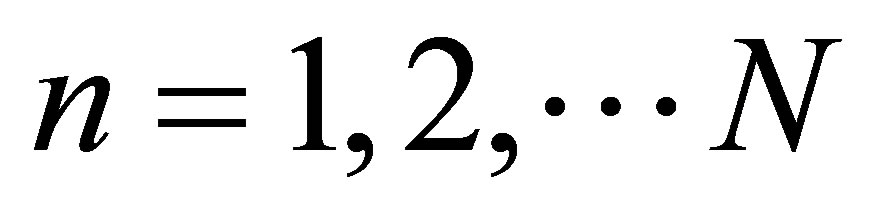 .
.
From Equation (8), the 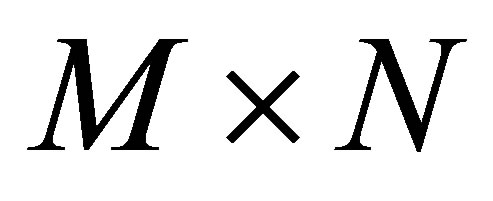 simultaneous linear homogeneous equations with the unknown coefficients
simultaneous linear homogeneous equations with the unknown coefficients  are obtained. These linear equations can be solved as an eigenproblem. Hence, it is possible to estimate the natural frequencies and mode shapes of thin plate.
are obtained. These linear equations can be solved as an eigenproblem. Hence, it is possible to estimate the natural frequencies and mode shapes of thin plate.
2.3. Governing Equations of Circular Thin Plate
The vibration of an isotropic circular plate with constant thickness is well documented. The motion equation of a circular thin plate is similar to that of rectangular thin plate. The only difference is the conversion from Cartesian coordinates to polar coordinates. In polar coordinates, the differential equation of free vibration of a thin plate is:
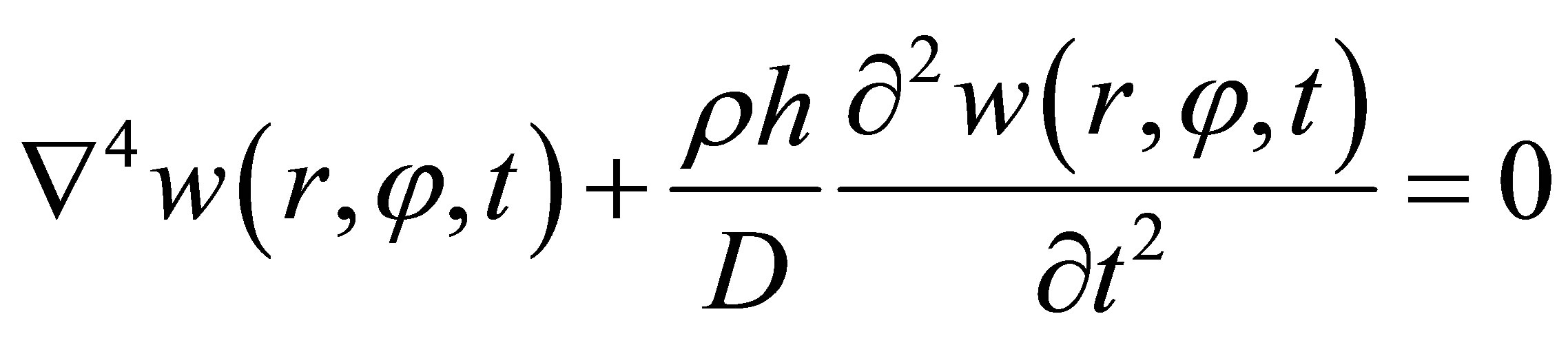 , (9)
, (9)
where  is the differential operator in polar coordinates,
is the differential operator in polar coordinates,
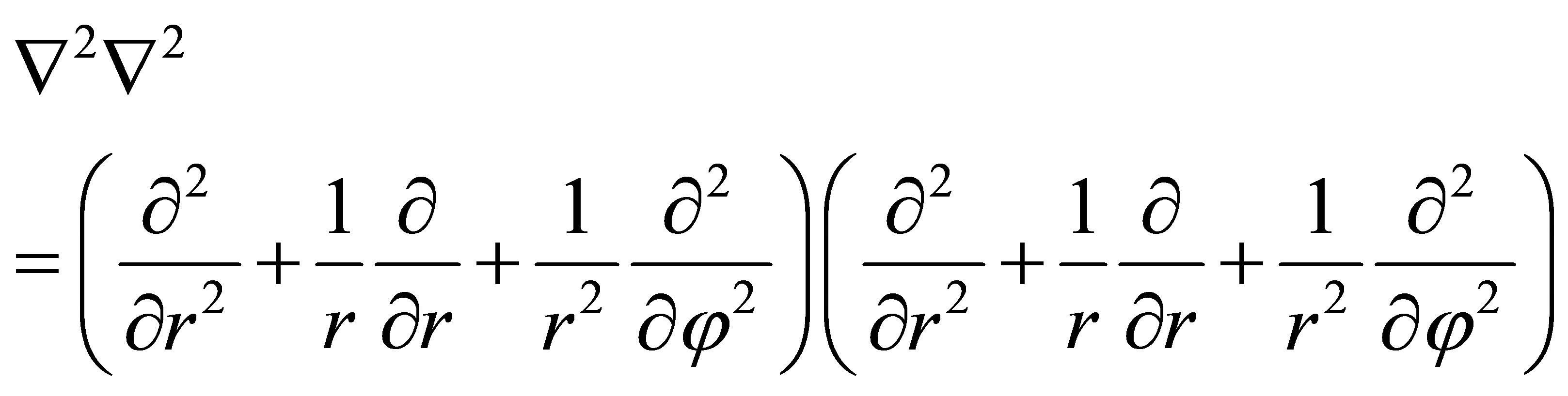 .
.
Defining a solution as Equation (3) and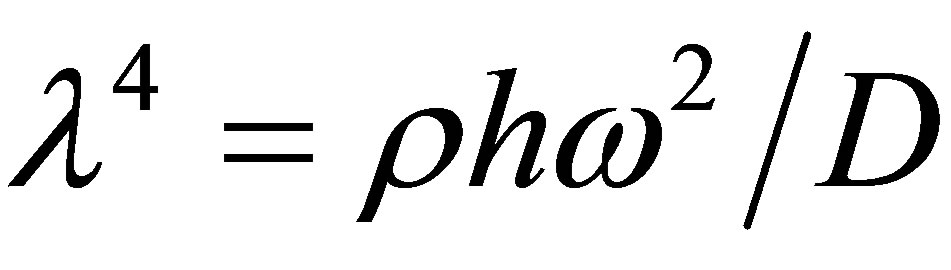 , and inserting them into Equation (9), the equation becomes:
, and inserting them into Equation (9), the equation becomes:
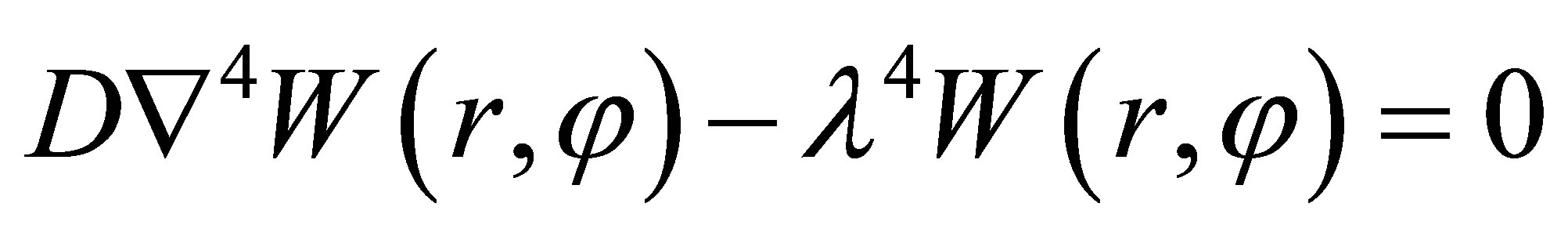 . (10)
. (10)
The solution of Equation (10) can be written as the sum of two distinct solutions, 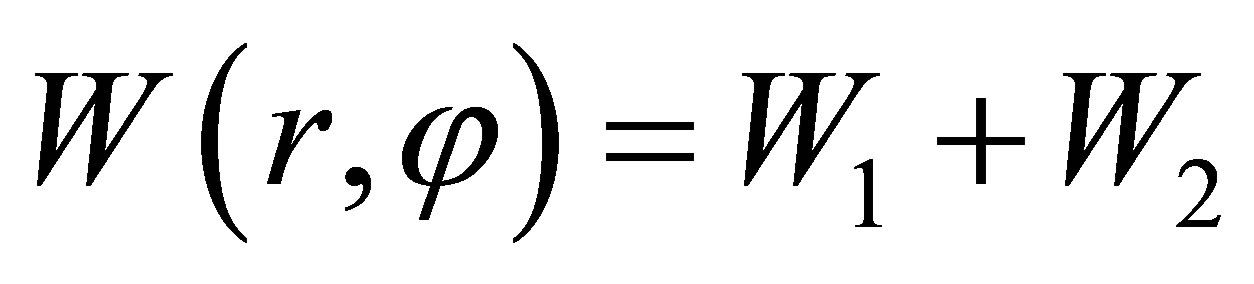 , where,
, where,
 . (11)
. (11)
Use the separation of variables and assume the mode shape as followings:
 . (12)
. (12)
Inserting Equation (12) into Equation (11) respectively, one obtains:
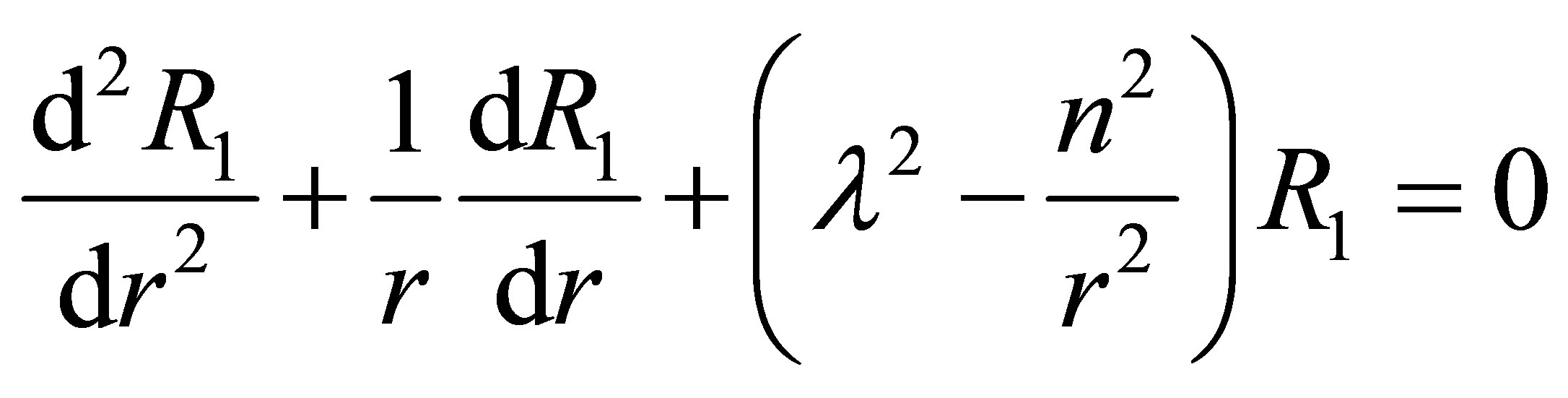 , (13)
, (13)
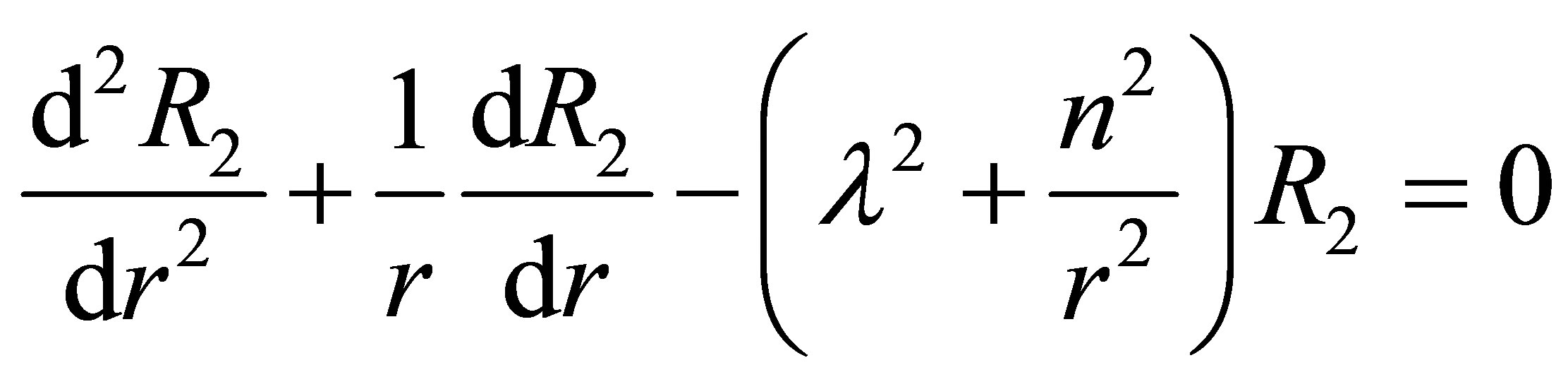 . (14)
. (14)
These two are special equations which are summed up in the study of some physical problems. The general solution of Equation (13) exists in terms of Bessel’s functions with constants  and
and :
:
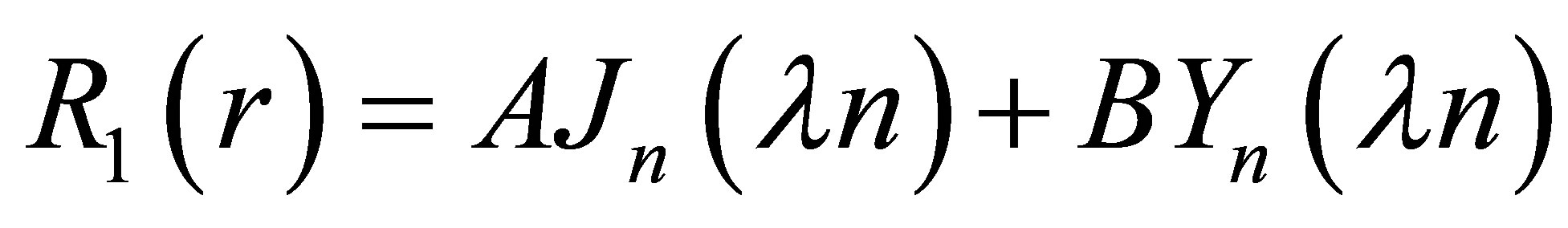 , (15)
, (15)
here 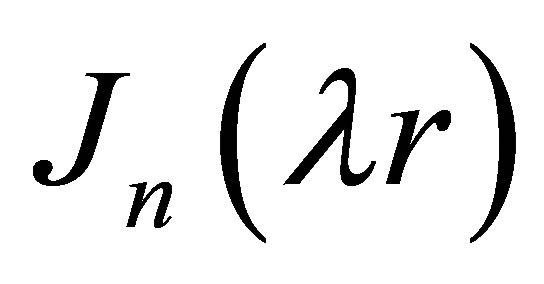 and
and 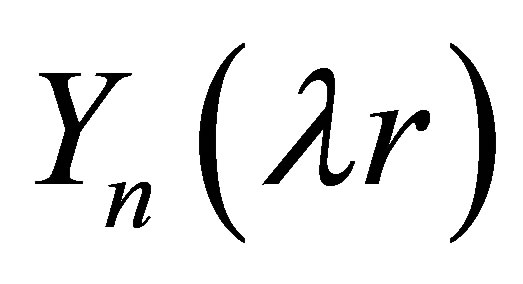 are, respectively, the first and second category n-order Bessel functions. And the general solution of Equation (14) can be expressed with the linear combination of
are, respectively, the first and second category n-order Bessel functions. And the general solution of Equation (14) can be expressed with the linear combination of 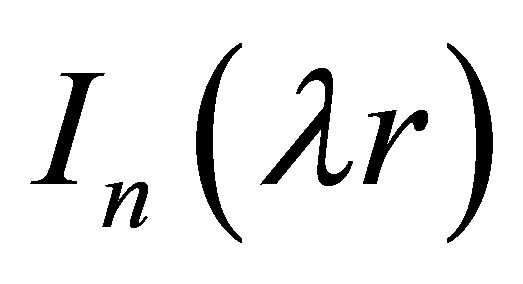 and
and 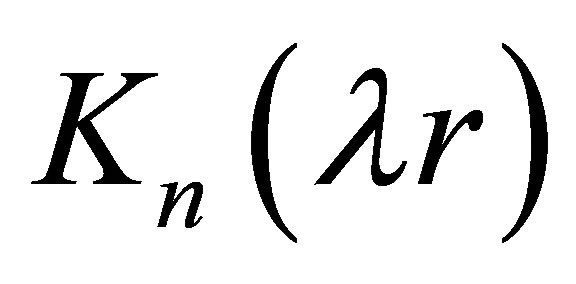 with constants
with constants ![]() and
and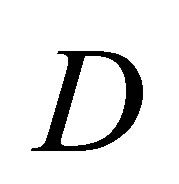 :
:
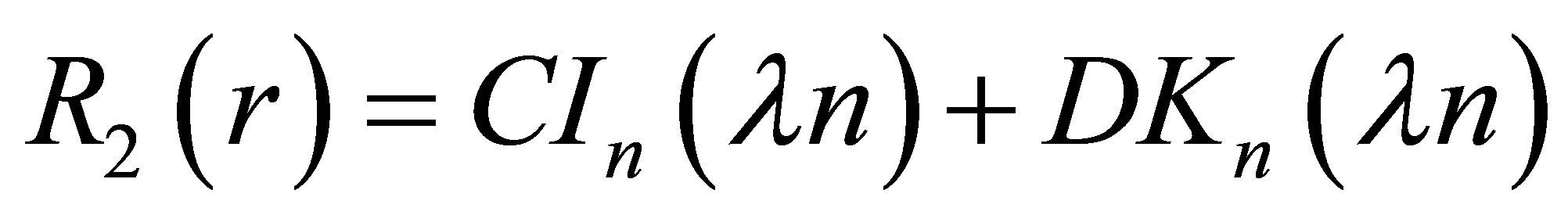 , (16)
, (16)
here 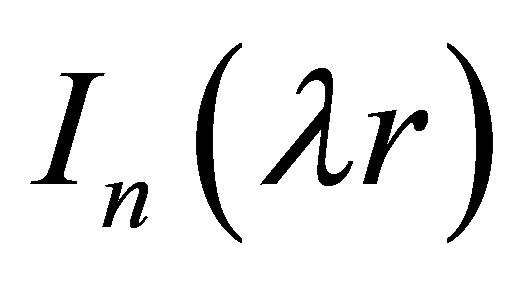 and
and  are the first and second category n-order Bessel functions of imaginary argument. Above all, the complete solution for displacement on the surface of the circular plate is described as following [20]:
are the first and second category n-order Bessel functions of imaginary argument. Above all, the complete solution for displacement on the surface of the circular plate is described as following [20]:
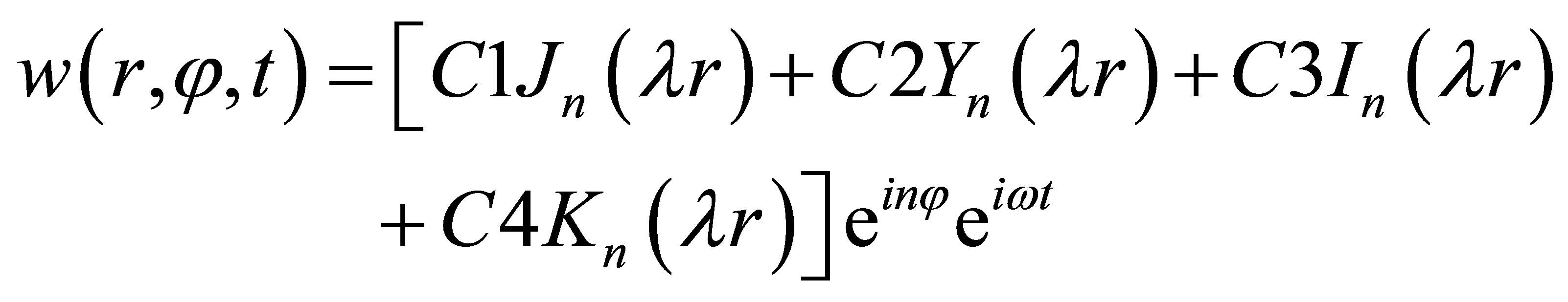 . (17)
. (17)
3. Free Vibration of 6-AFS’s Elastic Body
The 6-AFS studied in this paper is shown in Figure 2. The sensor consists of the base frame 1, lower E-type membrane 2, central solid cylinder 3, upper E-type membrane 4, middle force-transmitting loop 5, four lamellas 6 and upper force-transmitting loop 7. The base frame serving as a rigid support connects with the lower adapter by bolts. The lower and upper E-type membranes are connected by the cylinder. The middle force-transmitting loop links the upper E-type membrane and four lamellas. The upper force-transmitting loop connects with the upper adapter. For this sensor, components 2, 4 and 6 are elastic elements, and components 1, 3, 5, 7 seen as rigid bodies. The upper E-type membrane is used to detect tangential moments (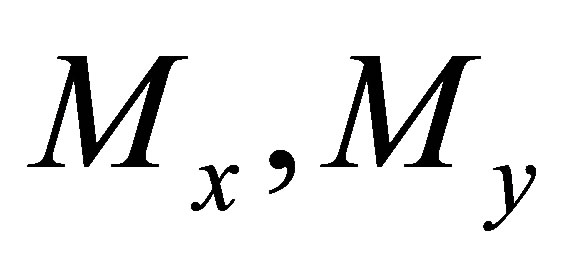 ), and the lower E-type membrane is used to sense the normal force (
), and the lower E-type membrane is used to sense the normal force (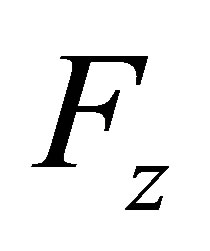 ) and both tangential forces (
) and both tangential forces (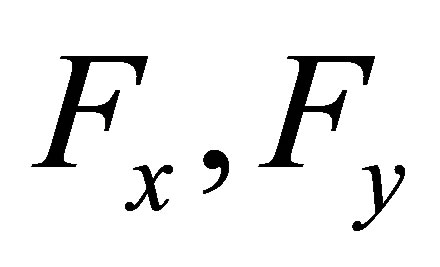 ). The four lamellas are responsive to the normal moment (
). The four lamellas are responsive to the normal moment (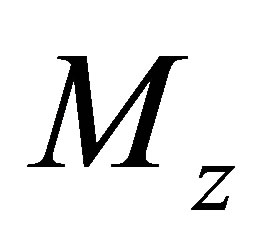 ). For the structure and material parameters of the sensor, please refer to Table 1 and Table 2.
). For the structure and material parameters of the sensor, please refer to Table 1 and Table 2.
During the analysis, the boundary of the rectangular thin plate is seen as one opposite edges clamped and the others free, as shown in Figure 3. The boundary of the upper and lower membranes are both viewed as the inner and outside edges clamped, as shown in Figure 4.
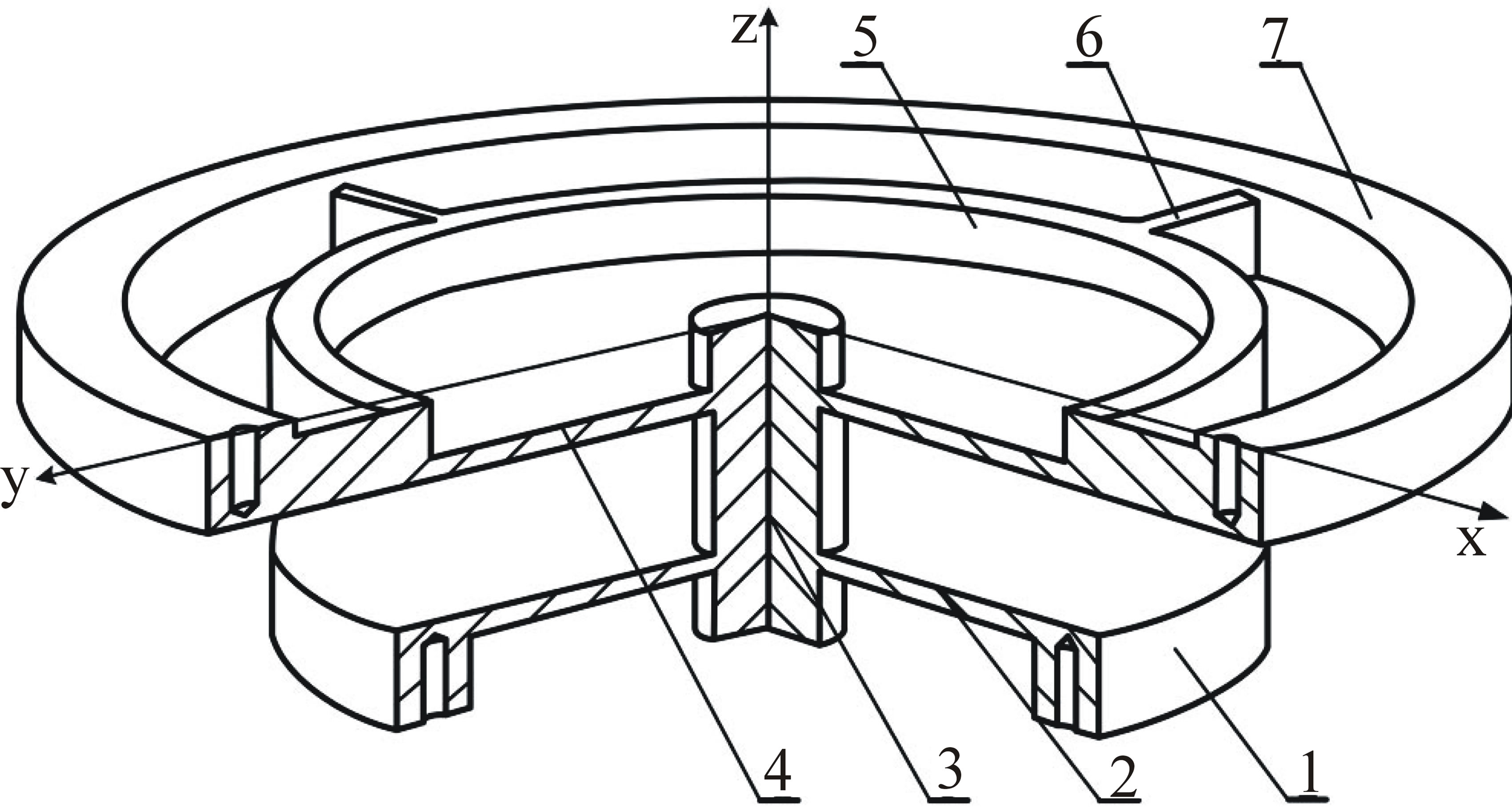
Figure 2. Structure of the six-axis force sensor.
Table 1. Structure parameters of the sensor [m].

Table 2. Parameters of LY12.

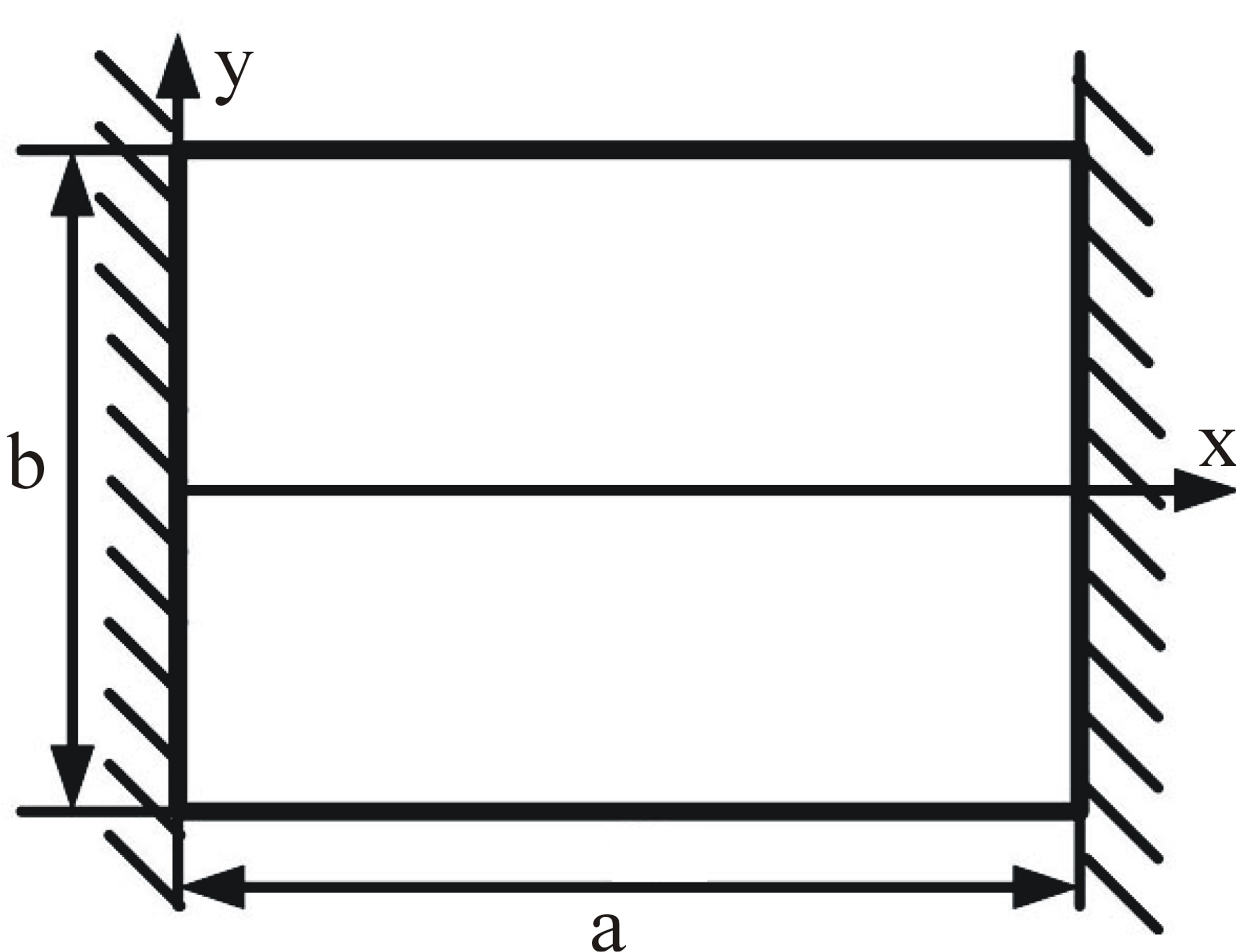
Figure 3. Schematic diagram of the lamella.
Figure 4. Schematic diagram of the membrane.
3.1. Free Vibration of Rectangular Plate
Assume that the basic function for mode shape is expressed as the following form:
 , (18)
, (18)
where: ;
;
 ;
;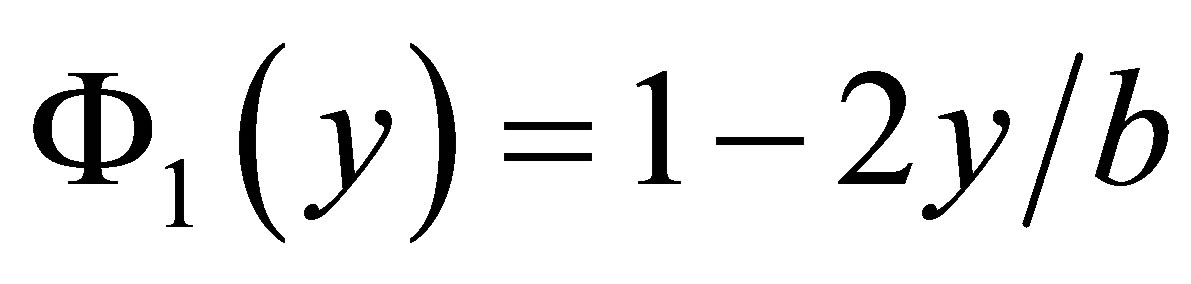 ;
;
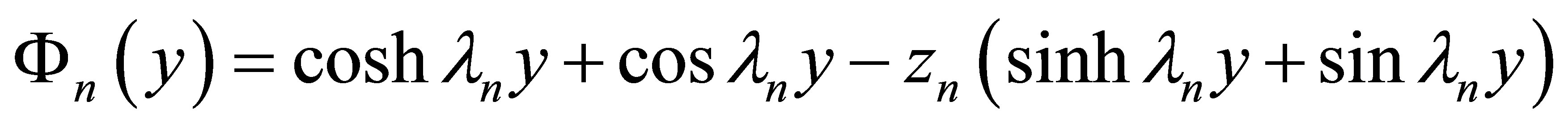 ,
, , in which:
, in which:
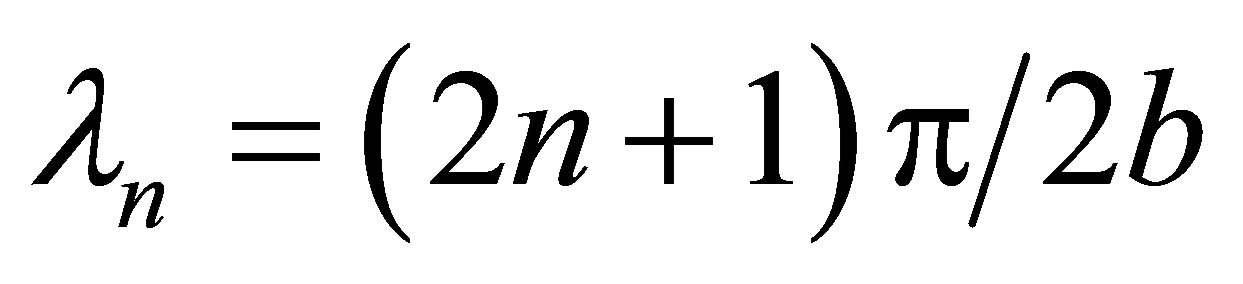 ;
;
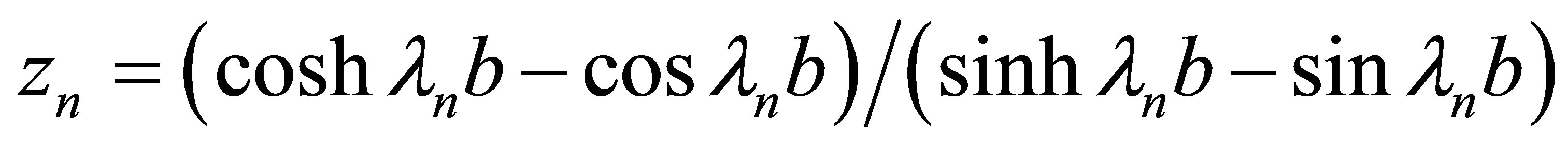 ,
, .
.
In this paper, let 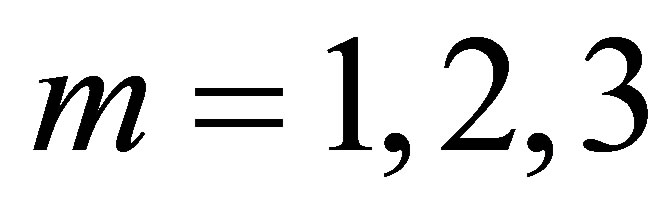 and
and 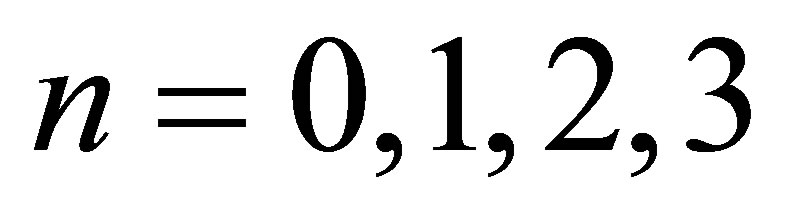 to calculate the natural frequencies and corresponding mode shapes of the plate. The forms of these basic functions are list in Table 3. Then the mode shape of the thin plate can be expressed as a linear combination of these 12 basic functions as follow:
to calculate the natural frequencies and corresponding mode shapes of the plate. The forms of these basic functions are list in Table 3. Then the mode shape of the thin plate can be expressed as a linear combination of these 12 basic functions as follow:
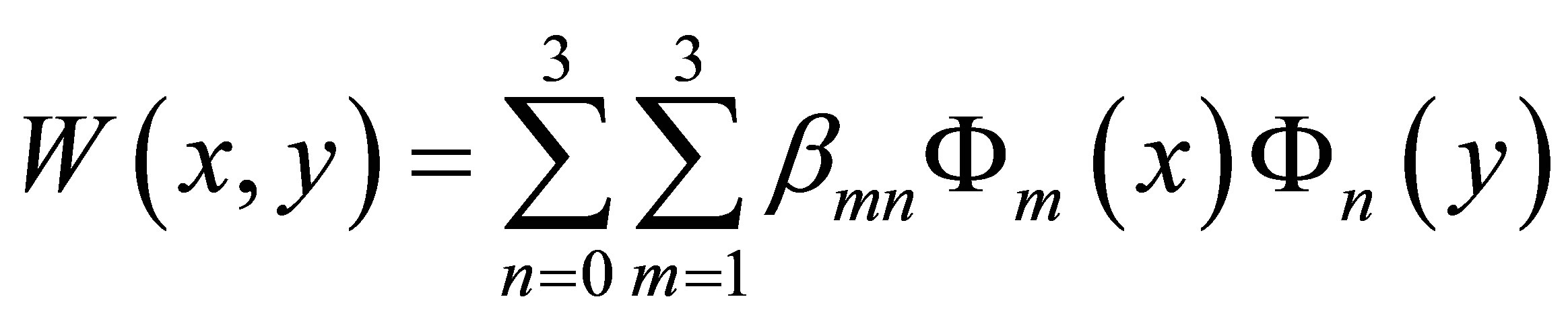 . (19)
. (19)
Insertion of Equation (19) into Equations (6) and (7) leads to  and
and . According to Equation (8), a set of 12 simultaneous linear homogeneous equations with
. According to Equation (8), a set of 12 simultaneous linear homogeneous equations with 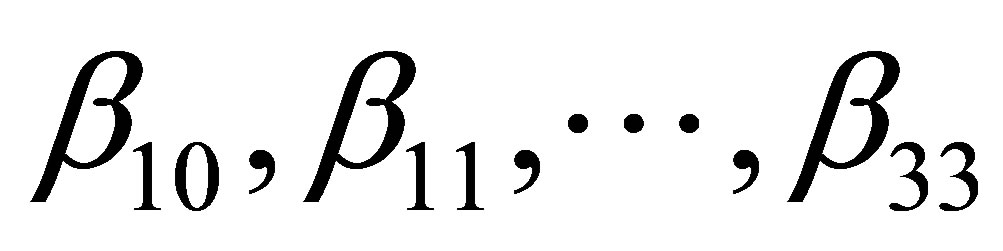 as the unknown parameters are obtained. Because the mode shape is existent, the determinant of the obtained equations must be zero and then get the natural frequency equation. Due to the huge computation, the software MATLAB is adopted to help calculate natural frequencies and mode shapes. In the present paper, the lowest six frequencies and mode shapes are obtained as shown in Table 4. The simulation diagrams of mode shapes are shown in Figure 5.
as the unknown parameters are obtained. Because the mode shape is existent, the determinant of the obtained equations must be zero and then get the natural frequency equation. Due to the huge computation, the software MATLAB is adopted to help calculate natural frequencies and mode shapes. In the present paper, the lowest six frequencies and mode shapes are obtained as shown in Table 4. The simulation diagrams of mode shapes are shown in Figure 5.
3.2. Free Vibration of Membranes
The boundary conditions of the membranes as shown in Figure 4 are given as follow:
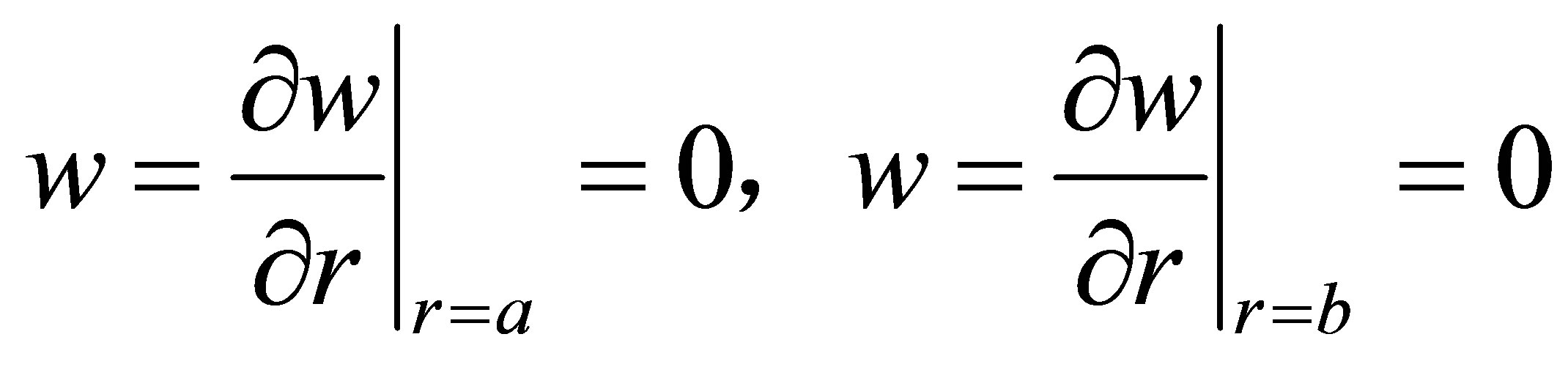 . (20)
. (20)
Substituting Equation (9) and Equation (17) into Equation (20) leads to the following linear equations:
 (21)
(21)
In order to make this homogenous equations have a nonzero solution, its coefficient determinant must be zero, namely:
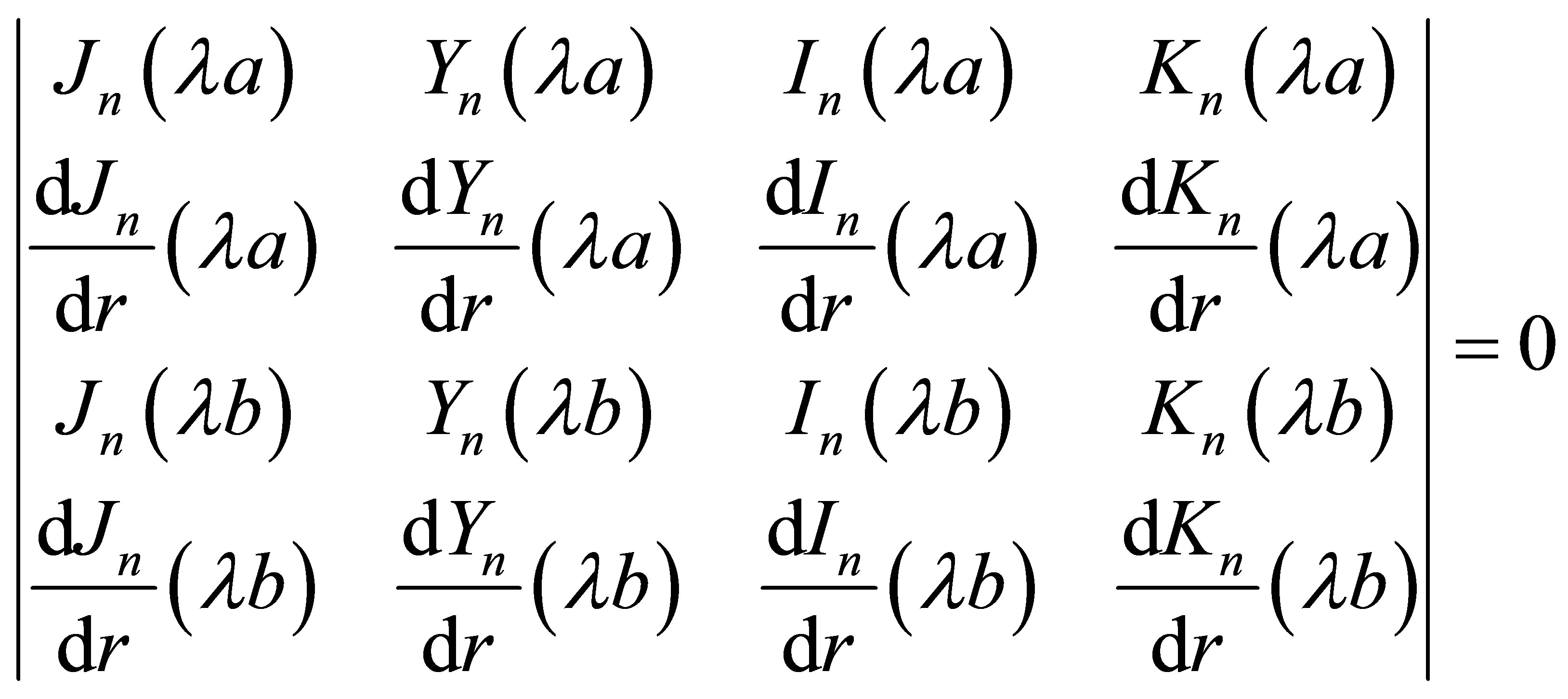 (22)
(22)
Table 3. The form of Φm(x)Φn(y).

Table 4. Natural frequencies and mode shapes.
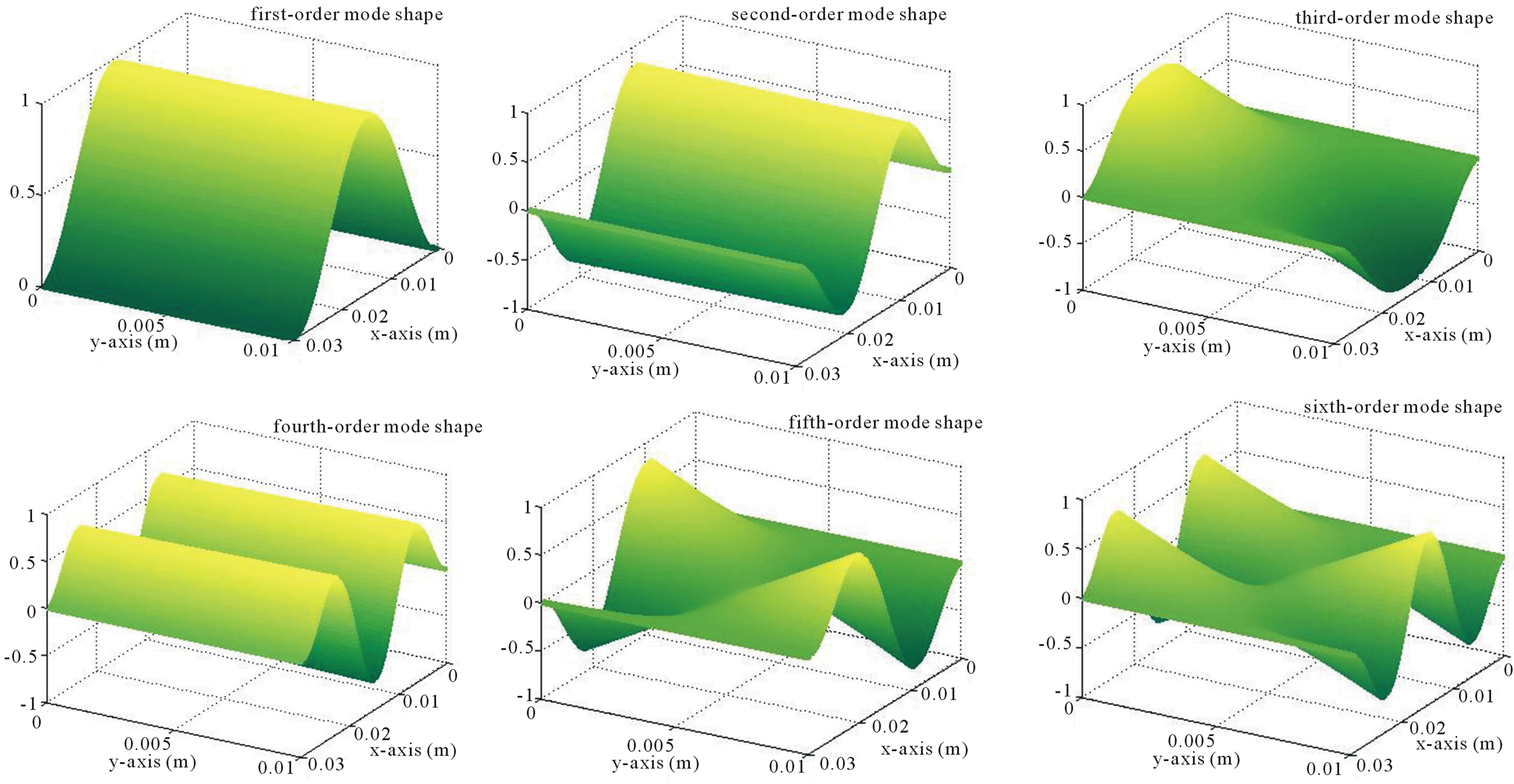
Figure 5. Simulation diagrams of the mode shapes.
Figure 6. Simulation diagrams of the mode shapes.
Table 5. Values of λnm.

Table 6. Natural frequencies and mode shapes.

Equation (22) is the natural frequency equation of the annular thin plate. According to the nature of Bessel functions, for any nonnegative integer![]() , it has infinitely many solutions
, it has infinitely many solutions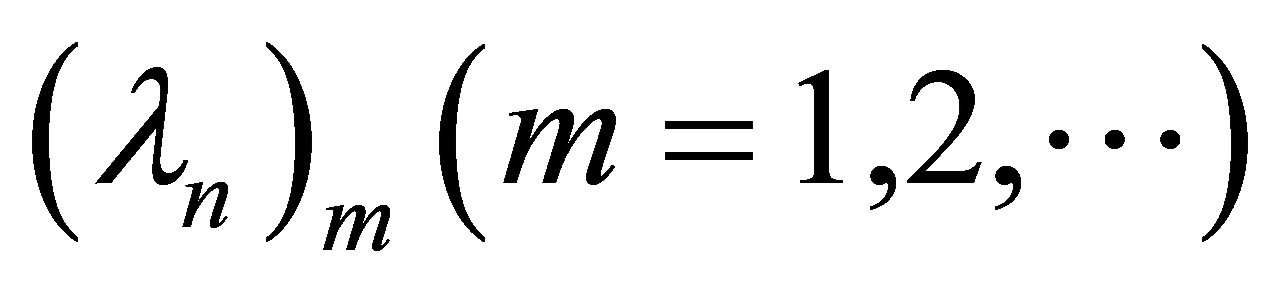 . One defines
. One defines  as the mth root of Equation (22) when the circumferential mode number is
as the mth root of Equation (22) when the circumferential mode number is![]() . Table 5 shows the first four roots when
. Table 5 shows the first four roots when ![]() is set to 1,2,3,4 respectively. Then the natural frequency is given by:
is set to 1,2,3,4 respectively. Then the natural frequency is given by:
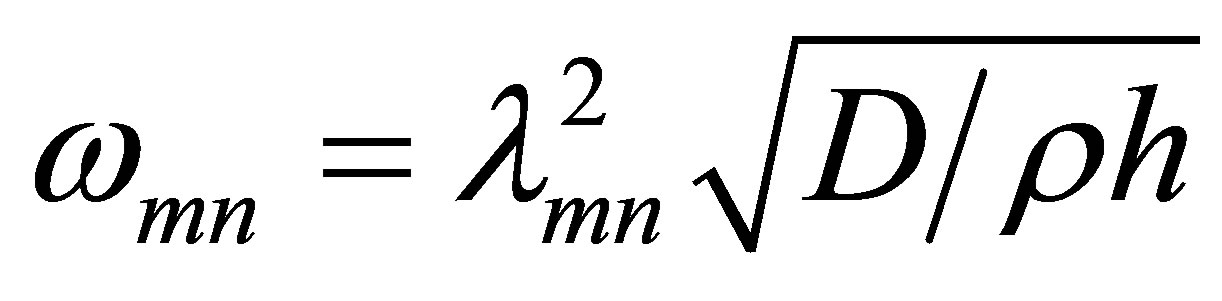 (23)
(23)
Substituting  into Equation (21) leads to the values of
into Equation (21) leads to the values of 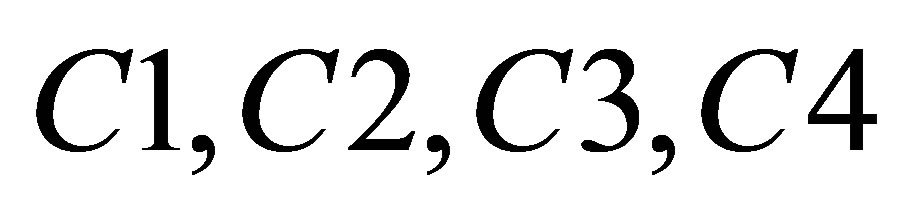 and then obtains the mode shapes. Table 6 and Figure 6 respectively show the natural frequencies and mode shapes, and simulation diagrams by software MATLAB with
and then obtains the mode shapes. Table 6 and Figure 6 respectively show the natural frequencies and mode shapes, and simulation diagrams by software MATLAB with .
.
4. Conclusion
In this paper, Rayleigh-Ritz method and the separation of variables method are introduced to analyze the free vibrations of the elastic bodies (the lamellas and the membranes) of the 6-AFS based on double layer E-type membrane. Through derivation, the analytical expressions of the natural frequencies and corresponding mode shapes are obtained and simulated by MATLAB. And the theoretical results are in good agreement with the actual situation. The analytical results of free vibrations have great significance to the follow-up studies about the dynamic response of the force vibration of thin plates. And it is also available to verify the correctness of the numerical methods.
5. Acknowledgements
This work is supported by the National Natural Science Foundation of China under Grant No. 51175001 and Anhui Provincial Natural Science Foundation under Grant No. 11040606M144.
REFERENCES
- J. K. Paik, B. H. Shin, Y. B. Bang and Y. B. Shim, “Development of an Anthropomorphic Robotic Arm and Hand for Interactive Humanoids,” Journal of Bionic Engineering, Vol. 9, No. 2, 2012, pp. 133-142. Hdoi:10.1016/S1672-6529(11)60107-8
- G. De Maria, C. Natale and S. Pirozzi, “Force/Tactile Sensor for Robotic Applications,” Sensors and Actuators A: Physical, Vol. 175, 2012, pp. 60-72. Hdoi:10.1016/j.sna.2011.12.042
- T. Yoshikawa and T. Miyazaki, “A Six-Axis Force Sensor with Three-Dimensional Cross-Shape Structure,” IEEE International Conference on Robotics and Automation, Scottsdale, 14-19 May 1989, pp. 249-255. Hdoi:10.1109/ROBOT.1989.99997
- Q. K. Liang, D. Zhang, Q. J. Song, Y. J. Ge, H. B. Cao and Y. Ge, “Design and Fabrication of a Six-Dimensional Wrist Force/Torque Sensor Based on E-Type Membranes Compared to Cross Beams,” Measurement, Vol. 43, No. 10, 2010, pp. 1702-1719. Hdoi:10.1016/j.measurement.2010.09.010
- A. G. Song, J. Wu, G. Qin and W. Y. Huang, “A Novel Self-Decoupled Four Degree-Of-Freedom Wrist Force/ Torque Sensor,” Measurement, Vol. 40, No. 9-10, 2007, pp. 883-891. doi:10.1016/j.measurement.2006.11.018
- Y. Haddab, Q. Chen, P. Lutz, “Improvement of Strain Gauges Micro-Forces Measurement Using Kalman Optimal Filtering,” Mechatronics, Vol. 19, No. 4, 2009, pp. 457-462. Hdoi:10.1016/j.mechatronics.2008.11.012
- D. Z. Xu, Z. C. Wu and Y. J. Ge, “The Solution to and the Analysis with Cross-Coupling Matrix of Six-Axis Wrist Force Sensor for Robot,” Chinese Journal of Scientific Instrument, Vol. 26, No. 1, 2005, pp. 75-80.
- Y. F. Xing and L. Bo, “Characteristic Equations and Closed-Form Solutions for Free Vibrations of Rectangular Mindlin Plates,” Acta Mechanica Solida Sinica, Vol. 22, No. 2, 2009, pp. 125-136.
- A. W. Leissa, “Vibration of Plates,” Office of Technology Utilization, Washington, 1969.
- S. Ilanko, “Comments on the Historical Bases of the Rayleigh and Ritz Methods,” Journal of Sound and Vibration, Vol. 319, No. 1-2, 2009, pp. 731-733. Hdoi:10.1016/j.jsv.2008.06.001
- L. Dozio, “On the Use of the Trigonometric Ritz Method for General Vibration Analysis of Rectangular Kirchhoff Plates,” Thin-Walled Structure, Vol. 49. No. 1, 2011, pp. 129-144. Hdoi:10.1016/j.tws.2010.08.014
- X. H. Si, W. X. Lu and F. L. Chu, “Modal Analysis of Circular Plates with Radial Side Cracks and in Contact with Water on One Side Based on the Rayleigh-Ritz Method, ” Journal of Sound and Vibration, Vol. 331, No. 1, 2012, pp. 231-251. Hdoi:10.1016/j.jsv.2011.08.026
- J. N. Reddy, “An Introduction to the Finite Element Method,” 2nd Edition, McGraw-Hill, New York, 1993. Hdoi:10.1007/978-3-642-83535-3_3
- I. Ramu and S. C. Mohanty, “Study on Free Vibration Analysis of Rectangular Plate Structures Using Finite Element Method,” Procedia Engineering, Vol. 38, No. 1, 2012, pp. 2758-2766. Hdoi:10.1016/j.proeng.2012.06.323
- G. Akhras and W. Li, “Stability and Free Vibration Analysis of Thick Piezoelectric Composite Plates Using Spline Finite Strip Method,” International Journal of Mechanical Sciences, Vol. 53, No. 8, 2011, pp. 575-584. Hdoi:10.1016/j.ijmecsci.2011.05.004
- C. Shu, W. X. Wu, H. Ding and C. M. Wang, “Free Vibration Analysis of Plates Using Least-Square-Based Finite Difference Method,” Computer Methods in Applied Mechanics and Engineering, Vol. 196, No. 7, 2007, pp. 1330-1343. Hdoi:10.1016/j.cma.2006.09.008
- P. Zhu and K. M. Liew, “Free Vibration Analysis of Moderately Thick Functionally Graded Plates by Local Kriging Meshless Method,” Composite Structures, Vol. 93, No. 11, 2011, pp. 2925-2944. Hdoi:10.1016/j.compstruct.2011.05.011
- S. A. Eftekhari and A. A. Jafari, “A Mixed Method for Free and Forced Vibration of Rectangular Plates,” Applied Mathematical Modeling, Vol. 36, No. 6, 2012, pp. 2814-2831. Hdoi:10.1016/j.apm.2011.09.050
- S. Timoshenko and S. Woinowsky-Krieger, “Theory of Plates and Shells,” 2nd Edition, McGraw-Hill, Inc., New York, 1959.
- R. K. Jain, “Vibrations of Circular Plates of Variable Thickness under an Inplane Force,” Journal of Sound and Vibration, Vol. 23, No. 4, 1972, pp. 407-414. Hdoi:10.1016/0022-460X(72)90499-3

