Received 5 November 2015; accepted 12 January 2016; published 15 January 2016

ABSTRACT

The original modified method of the direct delayed reaction has been used for the evaluation of food-obtaining strategy across spatial learning tasks in T-maze alternation. The optimal behavioral algorithms for each experimental day have been identified so that the animals obtain maximum possible food amount with minimal number of mistakes. Markov chain method has been used for the prognosis of rat’s behavioral strategy during the spatial learning task. The learning and decision-making represent the probabilistic transition process where the animal choice at each step (state) depends on the learning experience from previous step (state).

Keywords:

Delayed Reactions, Behavioral Algorithm, Markov Chain

1. Introduction

Both humans and animals live in a rich world of constantly changing external signals, thus the detection of changes and adequate reaction to environmental variation is crucial for the survival and successful adaptation. The learning and decision-making abilities are essential for adaptive behavioral strategy.

With no doubt, the behavioral studies remain the most prominent tool for exploring neural mechanisms of learning, memory and decision-making, though the past year experiments in behavioral and cognitive neuroscience [1] [2] have shaped innovate interdisciplinary approaches integrating the findings from different fields of science. Among them are widely-used mathematical-statistical methods [3] - [9] . At the same time, as a result of cross-disciplinary studies, various equations expressing biological relations gain a prominent position within mathematics [10] . Mathematical approach is believed to explain all phenomena where at least one variable varies towards other variables or affects them [11] [12] .

The probabilistic and stochastic processes in cognitive neuroscience are considered as constitute foundations of learning and decision-making [9] [10] [13] - [16] . Application of algebraic expressions has been proposed for description of learning processes [17] - [19] . More explicit mathematical methods are suggested for assessment of cognitive mechanisms involved in the adaptive learning, repeated decision tasks, reinforcement, and strategic changes [20] . The learning ability is studied in a binary choice task, where subjects have to choose from two possibilities (correct vs. incorrect) and the authors assume that the answers follow Bernoulli distribution that depends on a hidden state, reflecting the subject’s performance [21] . The probability that animals perform better than by chance is quantified and trial by trial performance is estimated. To develop a dynamic approach for analyzing learning experiments with binary response (correct, incorrect), state-space model of learning is introduced.

The question arises of how we go about understanding the probabilistic and stochastic processes that groundwork learning and memory. Due to a large number of possible parameters involved in learning, memory, and formation of adequate behavioral strategy, sometimes it seems difficult to generalize the results of behavioral studies. From this point, mathematical approach to the problem in general, and quantification of the measured parameters in particular, should be considered as the most reasonable means to identify the behavioral features and to interpret numeric data. Nowadays, such attitude is rather common to behavioral studies. Beside the wide range of traditional statistical methods used for analysis of behavioral parameters, different mathematical approaches and models are proposed for the data analysis in ethology, psychology, neuroscience, etc. [21] - [26] .

Markov chains are one of the basic tools in modern statistical computing, providing the basis for numerical simulations conducted in a wide range of disciplines. This mathematical technique undergoes transitions from one state to another through a set of values which process can take. Every state depends only on the current state and not on the sequence of events that precede it. Markov chains have many applications in biological modeling [2] [13] [14] [18] [21] [23] [27] [28] . They are widely applied in neuroscience research, including behavioral studies, neuron assemblies, ion channels and others [7] [14] [22] [29] , are the output of the Markov chains which can be different variables, for instance, the decision, or animal’s motor output and neural activity [13] [17] [24] [30] [31] . Markov chains are also used in simulations of brain function, such as the activity of mammalian neocortex [30] .

There are several ways we may go while studying cognitive abilities. We can simply observe, record and analyze neurobiological, behavioral conformities, or/and make an attempt to construct quantitative models in order to understand the computations that underpin cognitive abilities. What different cognitive studies share is the attempt to identify the involvement of various brain states in the behavioral processes. Sometimes the segmenting of observed and measured behavioral processes into consequence elements is needed to explore and quantify transitions between them. Thorough inquiry of animal behavioral conformities across learning process gave huge body of information on behavioral consequences which can be tested with Markov chains analysis. Markov chains have shown to provide better estimation of learning conformities in comparison with other methods used to infer from behavior data treatment. Such modern approaches contribute in studying the cognitive abilities and their behavioral correlates.

From neurobiological point of view, it is interesting to perform extrapolation on the basis of experimental data in order to establish quantitatively the degree of learning and the dynamics of the memory. The results of behavioral experiments can be predicted by means of the mathematical model using one of the main objects of probabilistic-statistical investigation-Markov chains [11] . In this paper the mathematical apparatus describing the direct delayed reactions using the discrete-time Markov chains is considered.

The experiments with using a modified method of direct delayed reactions made it possible to observe the learning process of the animals along with establishing the maximal delay and identifying an optimal algorithm of minimum errors and maximal reward. Here we will discuss the development of optimal algorithms and the dynamics of variability at delays of different duration.

2. Methods

2.1. Subjects

31 albino rats of both sexes (with an average weight of 150 g) have been examined. The animals were individually housed in stainless steel cages in conditions of natural light-dark cycle and temperature of 20˚C ± 1˚C. The rats had free access to food and water throughout the whole experiment.

2.2. Apparatus

The rats were tested in a 25 cm-walled wooden T-maze (64 cm in length). The start compartment arm (47 cm in length) joined the two goal arms, each of which was 17 cm in width. Wooden feeders were situated at the far end of each goal arm. The floor under the feeders was electrified. The light and audio signal sources were attached to the top of starting compartment to study rat spatial learning through the different behavioral tasks using different experimental schemes (Figure 1).

2.3. Procedure

The experiments were conducted on white rats using a modified method of direct delayed reactions [16] . Rats were trained in a T-maze-based spatial learning task that required animals to make trial-by-trial choices contingent upon their previous experience. The aim of the experiment was to fixate the complex perception of food in conditions of two feeders. Ten trials were conducted daily with a strictly defined time-spatial program, with strictly defined sequence of signaling feeders, the time interval between trials and the duration of delay. Before the delay, the animal was allowed to move in the experimental cabin without the intervention of the experimenter and obtain food in any feeder defined by the program. The rat could first run up to the feeder with food, and then to an empty one, or vice versa, and if it did not return to the starting compartment, the experimenter returned it with force. The animal was allowed to return from the feeder with food without correction to the start compartment so that it did not run to the empty feeder. After the delay the door of start compartment was opened and the animal had the possibility of free behavior. Both direct and indirect reactions were registered. During direct reaction the animal got food, while in case of indirect reaction did not. In the protocol the right move performed by the rat was marked by “1”, and incorrect-by “0”. The distribution of zeroes and ones was recorded in the protocol (Table 1).

Proposed approach gave us the possibility to characterize animal behavior and describe a learning algorithm [16] . For example, the sequence “11001110” means that in pre-delayed behavior (first 5 digits), the animal leaves the starting compartment without the interference of the experimenter (1), performs a proper move and runs to the feeder, where it has got food in the previous trial (1). This time it had not received food, since it was not provided by the program (0). So it was necessary to make the correction of the movement to the opposite feeder, as the food was placed there. The animal corrects its movement after the interference of the experimenter (0) and returns to the starting compartment (1). The last three digits of the given algorithm describe delayed reactions. The animal itself leaves the starting compartment (1), performs a right move and runs towards the

feeder, where before delay it has got reinforcement (1). After this the experimenter returns the animal to the starting compartment (0). Table 2 demonstrates the dynamics of delayed reactions’ algorithms for pre-delayed behavior and describes the process of optimal behavioral strategy formation. The obtained algorithms are applied for further mathematical analysis.

The schematic diagram of behavioral strategies based on obtained algorithms for one of the experimental days is presented on Figure 2. The diagram shows different behavioral strategies identified as bed (1,2,3), medium (4,5,6), good (7,8,9) and the best (10,11,12) learning algorithms.

2.4. Mathematical Description of Behavioral Algorithm

Description of Markov chain is as follows: we have a set of experimental trials (states). The process starts in one of these states and moves successively from one state to another. Each move is called a step. If the chain is currently in state n_i then it moves to state n_i at the next step with a probability denoted by P_ij, and it does not depend upon which states the chain was at before the current state. In Markov chain the probabilities P_ij are called transition probabilities. The process can remain in particular state, which occurs with probability P_ij. An initial probability distribution, defined on n, specifies the starting state. Usually this is done by specifying a particular state as the starting state of behavioral experiment. We present a behavioral method for estimating these functions.

3. Results and Discussion

The initial state of a system or a phenomenon and a transition from one state to another appear to be principal in the explanation of Markov chain. In our experiments the initial state is 0 or 1; while the transition may occur from 0 to 1, or vice versa from 0 to 0, or from 1 to 1.

For studying Markov chains it is necessary to describe the probabilistic character of transitions. It is possible

that the time intervals between transitions be permanent.

All states n (in our case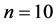) are numbered. If the system is described by Markov chain, then the probability that the system will moves from state i to 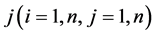during the next time interval depends only on the variables i and j and not on the behavior of the system before the transition to state i. In other words, the P_ij probability that the system will transit from state i to j does not depend on the type of behavior before state i. Proceeding from the explanation and features of the probability it is easy to assume that

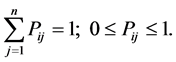
For the modeling the above described experiment, it is convenient to define Markov chain as follows: let’s say 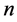number of trials is conducted; if across consecutive trials the conditional probability that any event occurred in trial (we consider the results of previous trials as known) depends only on the result of the last n^th trial and does not depend on previous trials, one can say that Markov condition holds. The observed process is called “Markov chain”―random process with discrete (finite) state-space.

Let us assume that the observed behavioral process appears to be random chain with Markov properties, the possible values of which are 0 and 1, and the transition probabilities are determined (estimated) using obtained empirical frequencies. As the initial state is 0 or 1, the transition may occur from 0 to 1, from 0 to 0, or from 1 to 1. We consider the question of determining the probability that, given the chain is in state i, it will be in state j across behavioral treatment. Simply, if we will know the probability that the result of the first trial is 0, then we can define the probability that during the trial n^th result will also be 0

Let the conditional probability for transition from initial state 0 for trial n to state 1 in trial 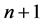be written as:

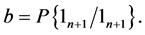
It should be noted that the events 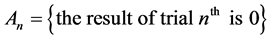and 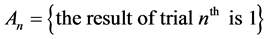create a complete system of events (i.e. a system of such events, one of which necessarily occurs in any trial and any two different events cannot occur simultaneously). Therefore, the event can be denoted as follows:

.

It is easy to determine the probability of the event using total probability formula:

,

where and are conditional probabilities, i.e. the transition probabilities of Markov chain.

Now we need to recall formulas:

,

which give recurrence equation for the reliable probability:

(1)

In the general case. Therefore when. As when, from the equation (1) we gain formula:

.

In the case, we obtain:

Analogously, when . The probabilities p and q are called “final” probabilities. They depend on transition probabilities only and do not depend on the initial state. For a big n we can assume that the process is “balanced”―it’s probabilities (independently from n) approximately equal to p or q. This feature of Markov process (chain) is very important in applied science and bears the name of ergodic.

In the general case finding solutions to Equation (1) are very difficult, but in case when P_n does not depend on n, i.e., stationary equation can be written:

(2)

The solution of stationary Equation (2) is simple:

(3)

As solution of stationary Equation (2) is known, we can get the general solution. We only have to suppose that

(4)

If we substitute (4) into the Equation (1) for P_n, we get:

.

From the stationary Equation (2) the following recurrence equation is correct

, from which

According to assumption (4) we get which gives possibility to move from to P_n.

, and

(5)

The Equation (5) can be used to predict the experimental results: if we know values for probabilities a, b and P₁ for the first n number of trials, we can calculate the probability of getting 0 the result of trail will be.

The probabilities a, b and P₁ can be estimated by corresponding empirical frequencies.

To illustrate this, let’s discuss in detail an algorithm of calculation of the probability (prognosis) using the Equation (5) on the basis of the data of 7^th column () of Table 1.

1)

Analogically, the following results are obtained for 8^th - 14^th columns of Table 1:

2)

3)

4)

5)

6)

7)

8)

4. Conclusion

In this paper, the original modified method of the direct delayed reaction on the basis of results of the Markov chains theory is developed. The proposed mathematical apparatus allow to calculate the probability (prognosis) that the results of the following trail will be 0 if the estimates of the probabilities a, b and P₁ for the first n number of trials are known. It should be noted that the probabilities of possible events of the theoretically calculated reactions coincide with the experimental data. It gives us an opportunity to use widely the above described method in neurophysiological investigations. In addition, it is possible to use them also for delayed reactions carried out by indirect and alternate methods. If we imagine everyday experimental results as one trial, it will be possible to make a long-term prognosis of the animals’ behavior.

Cite this paper

Sulkhan N.Tsagareli,Nino G.Archvadze,OtarTavdishvili,MarikaGvajaia, (2016) The Prognosis of Delayed Reactions in Rats Using Markov Chains Method. Journal of Behavioral and Brain Science,06,19-27. doi: 10.4236/jbbs.2016.61003

References