Journal of Behavioral and Brain Science
Vol.4 No.1(2014), Article ID:41923,4 pages DOI:10.4236/jbbs.2014.41003
Multimodality Vessel Modeling Analysis for Cerebral Arteriovenous Malformation
1Philips Health Care, Philips Innovation Campus, Manipal University, Bangalore, India
2Philips IP&S, Philips Innovation campus, Bangalore, India
3Philips Research, Philips Innovation Campus, Bangalore, India
Email: *Kiran.kumary@philips.com
Received November 29, 2013; revised December 29, 2013; accepted January 7, 2014
ABSTRACT
Cerebral arteriovenous malformations (AVMs) are a type of vascular anomaly consisting of large intertwined vascular growth (Nidus) that is prone to serious hemorrhaging and can result in patient death if left untreated. Intervention through surgical clipping of feeding and draining vessels to the Nidus is a common treatment. However, identification of which vessels to clip is challenging even to experienced surgeons aided by conventional image guidance systems. The lumped modeling for the Cerebral Arteriovenous Malformation (CAVM) hemodynamic analysis is of high importance in clinical world. As part of the treatment planning for CAVM, it is difficult for doctors to assess the NIDUS part, which may get rupture while inserting catheter. In this paper, we have proposed a non-invasive method for assessing the hemodynamic condition of AVM. The measurement of flow and pressure without intervention along the vessel is a big challenge due to occlusion, bending and thinning of the vessel in Arteriovenous Malformation patients. In this paper, we analyzed a lumped model for the vascular malformation using various imaging multi-modalities that help to analyze CAVM Structures.
Keywords:Vessel Deformation; AVM; Lumped Model
1. Introduction
Cerebral Arteriovenous Malformation (CAVM) is an abnormal tangle of brain blood vessels where arteries shunt directly into veins with no intervening capillary bed which causes high pressure and hemorrhage risk. Intracranial Arteriovenous malformations (AVM) constitute usually congenital vascular anomalies of the brain. AVMs are composed of complex connections between the arteries and veins that lack an intervening capillary bed. A brain modeling of the Hemodynamics with physical properties of Cerebral AVM is important in understanding the dynamics of pressure flow relationships and implications of alterations in these properties with respect to pressure monitoring, logical approach to therapy and treatment.
The aim of this work is to compare the modeling analysis and modeling outputs using the different modalities— Digital Subtraction Angiogram (DSA), 3D-Rotational Angiogram (3D-RA), CT Angiogram (CTA), and MR Angiogram (MRA). The clinical outputs such as the pressure, flow rate, velocity of the blood flow at various vessel locations are determined by using the Lumped models. The input parameters are used for the simulations that are inferred from Modality. In the present work, we have compared the modeling approach for the Vessels complexity with data from 2D & 3D acquisition.
In the literature analysis, the modeling is based on the fluid dynamics of the vessel. It has some drawbacks on the analysis using various signals. In the lumped modeling, the analysis which was based on the electrical circuit analogy using WindKessel models was used to provide a computationally simple way to obtain information about the overall behavior of the Neurovascular system. The authors had proposed electrical parameters and derived a number of lumped models for blood flow and pressure variances in the Cerebral Arteries Windkessel and the lumped parameter models were used to simulate pressure and blood flow in the arterial system. In these models, electric potential and current are analogous to the average pressure and flow rate, respectively. A particular vessel (or group of vessels) is described by means of its impedance, which is represented by an appropriate combination of resistors, capacitors and inductors. figure 1 shows the complexity of CAVM that indicates the complex anatomy of the Vessel [1,2].
2. Methodology
The proposed methodology is common for different modalities that acquired for the Brain AVM patients using Philips Unit. The following steps are applied to any volume image:
1) Input data is MR angiogram (MRA) and Digital Subtraction Angiogram (DSA). The steps involved for both modalities looks similar, but only the network creation using lumped model varies with respect to radius and length.
2) Preprocessing of input image is performed using the preprocessed algorithm—smoothing, sharpness factor and enhancement filters for better visualization of the input dataset. The figure 2 shows the preprocessed image used for the analysis.
3) The vessel region is analyzed by drawing 3D ROI at different locations of vessel and in different frames of the volume. 3D ROI is implemented using the Philips Prosperity algorithm to draw and automatically propagated to all the slices, by applying interpolation technique. The ROI analysis segmentation is based on the seed point with specific threshold based segmentation to analyze particular region of vessel. This analysis helps to segment different locations of vessels of different frame positions for various modalities.
4) For each segmented vessel, the diameter, length is calculated for each part of the vessel branch. We have analyzed based on the shape descriptor algorithm to extract exact shape of the vessel and calculated the required vascular parameters needed for the lumped modeling. The figure 3 shows the ROI analysis and vascular parameters for the modeling [3].
5) The lumped model is based on the Windkessel model. These lumped models can be derived from electrical circuit analogies where current represents arterial blood flow and voltage represents arterial pressure. Resistances represent arterial and peripheral resistance that occur as a result of viscous dissipation inside the vessels, capacitors represent volume compliance of the vessels that allows them to store large amounts of blood, and inductors represent inertia of the blood [4].
6) The Resistance = pressure drop through the channel /flow = 8η L/π R4; l its length and µ is the fluid viscosity.
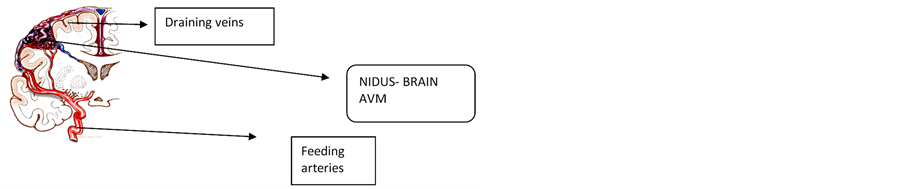
Figure 1. Cerebral Arteriovenous Malformation (CAVM).

Figure 2. Preprocessed MRA Data using preprocessed algorithm.

Figure 3. ROI analysis.
R is the radius
 (1)
(1)
where µ is blood viscosity, l and A are in respect length and cross section area of each arterial segment. Blood viscosity is a measure of the resistance of blood to flow, which is being deformed by either shear stress or extensional stress. This simulation has considered because blood viscosity will cause resistance against Blood flow crossing.
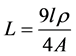 (2)
(2)
and ρ is blood density.
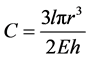 (3)
(3)
where r, E, h are in respect artery radius, Elasticity module and thickness of arteries [5,6].
7) For each segmented vessel, using windkessel model, we have derived the electrical model for the symmetrical and asymmetrical network for vessel analysis. The figure 4, shows the example of the Vessel deformation model for the symmetrical network and asymmetrical network, where the vessel is deformed in the one part of the branch of the vessel [7,8].
The figure 5 shows the vessel analysis model for the asymmetrical network, with combinations of two branches, with a node denotes the branch of each vessel.
3. Statistical Analysis
The statistical analysis for the lumped modeled using any modality DSA, MRA, CTA; 3D-RA is based on the Segmentation, ROI analysis as shown in figure 6 [9-11]. The quantification is performed using the statistical package using MATLAB. For each portion of the segmented vessel, the various statistical quantifications are applied to derive various results of the segmented image.
The following are the quantification of the segmented image with ROI analysis is completed as follows:
The output table 1 shows the example results for the drawn ROI analysis.
4. Results and Discussion
The implementation is done using MATLAB Software using 3D-RA dataset. The electrical model is derived for the vessel deformation with symmetric and asymmetric using clinical parameters. The clinical parameters are analyzed and converted in to electrical parameters which help to create a WindKessel model using R, L, C values. The RLC values and its combinations are modified based on the type of network and also type of vessel deformation. This leads to symmetrical network vessel deformation and asymmetrical vessel deformation.
This model is simulated and validated with clinical results and with mechanical outputs. The mechanical simulation is performed using ANSYS software. The effect of vessel deformation shows the clinical significance on the pressure and flow rate variation of the blood flow in AVM patients. Simulations were also performed using the phantoms and also using 2D-DSA images that are varying length with networks of symmetric and asymmetrical. In these simulations for various values of diameters are used to simulate the actual clinical scenario.
The results shows that for MRA image, the ROI analysis gives clear indication of the proper segmentation, which will be used for clinical diagnosis. The ROI analysis is based on the preprocessed algorithm, which determines the modeling accuracy of the input image.
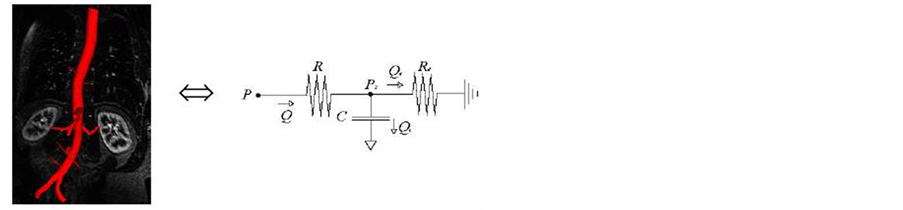
Figure 4. Vessel deformation lumped model.

Figure 5. Vesseld Analysis for Asymmetrical Netowrk.

Figure 6. ROI analysis and quantification.
5. Conclusion
In this paper, we have proposed a neurovascular vessel analysis for the multimodality dataset of 2D and 3D and simulated the vascular parameters using the model. This model research work is in progress to target more combinations of data sets to make it more common across all modalities. This work is based on Lumped Model and it
is validated through the Mechanical Model. The modeling outputs are used by doctors for the diagnosis, treatment planning for the AVM surgery and also for the AVM management.
Acknowledgements
I want to thank KMC Manipal in providing the datasets for this research from various modalities for AVM.
REFERENCES
- Y. B. Shi, P. Lawford and R. Hose, “Review of Zero-D and 1-D Models of Blood Flow in the Cardiovascular System,” BioMedical Engineering OnLine, Vol. 10, 2011, p. 33. http://www.ncbi.nlm.nih.gov/pmc/articles/PMC3103466/ http://dx.doi.org/10.1186/1475-925X-10-33
- T. F. Massoud, G. J. Hademenos, W. L. Young, E. Gao and J. Pile-Spellman, “Can Induction of Systemic Hypotension Help Prevent Nidus Rupture Complicating Arteriovenous Malformation Embolization? Analysis of Underlying Mechanisms Achieved Using a Theoretical Model,” AJNR American Journal of Neuroradiology, Vol. 21, 2000, pp. 1255-1267.
- “Modelling Cerebral Haemodynamics: A Move towards Predictive Surgery,” Edlong, 2007, Thesis Report.
- E. Gao and W. L. Young, “Theoretical Modelling of Arteriovenous Malformation Rupture Risk: A Feasibility and Validation Study,” Medical Engineering & Physics, Vol. 20, No. 7, 1998, pp. 489-501.
- Y. Zheng and J. Mayhew, “A Time-Invariant Visco-Elastic Windkessel Model Relating Blood Flow and Blood Volume,” Neuroimage, Vol. 47, No. 4, 2009, pp. 1371- 1380.
- “Experimental Model of Intracranial AVM in the Acute Stage,” Shinichi, Department of Neurology, Medical University, Fukushima, Neurological Medical Chir (Tokyo), 2005, pp. 288-293.
- T. Li, “AVM Compartments, Do They Modulate Nidal Pressures? An Electrical Network Analysis,” AJNS, 2012, pp. 173-180.
- Y. Cao, “Frequency-Independent Equivalent-Circuit Model for On-Chip Spiral Inductors,” IEEE Journal of SolidState Circuits, Vol. 38, No. 3, 2003, p. 419.
- M. S. Olufsen and A. Nadim, “On Deriving Lumped Models for Blood Flow and Pressure in the Systemic Arteries,” Mathematical Biosciences and Engineering, Vol. 1, No. 1, 2004, pp. 61-80.
- X. L. Zhu, “A Lumped Parameter Model of Coronary Flow to Analyze Time Intensity Curves Extracted from Angiograms Electrode-Rail Dielectrophoretic Assembly Effect: Formation of Single Curvilinear Particle-Chains on Spiral Microelectrodes,” Microfluidics and Nanofluidics, Vol. 9, No. 4-5, 2010, pp. 981-988.
- J. Kim, N. A. Thacker, P. A. Bromiley, et al., “A Simple Electrical Equivalence Model of Intracranial Cerebrospinal Fluid Pulsatility: Design and Validation in Healthy Normals” Proceedings of MIUA, Manchester, 4-5 July 2006, pp. 1-19.
NOTES
*Corresponding author.


