Journal of Behavioral and Brain Science
Vol. 2 No. 3 (2012) , Article ID: 22081 , 4 pages DOI:10.4236/jbbs.2012.23034
Interaction between Angiotensinergic System and GABAergic System on Thirst in Adult Male Rats
1Department of Biology, Science Faculty, Tarbiat Moallem University, Tehran, Iran
2Department of Physiology & Pharmacology, Pasteur Institute, Tehran, Iran
Email: shirazinejad2620@gmail.com, *naghdi@pasteur.ac.ir, sh_oryan@saba.tmu.ac.ir
Received August 30, 2011; revised October 13, 2011; accepted December 12, 2011
Keywords: Water Intake; Drinking; Angiotensinergic Receptors; GABAergic Receptors
ABSTRACT
Thirst is a subjective perception that provides the urge for human and animals to drink fluids and it is important for maintaining body fluid homeostasis and may arise from deficits in either intracellular or extracellular fluid volume. Gamma-aminobutyric acid (GABA) and Angiotensin (Ang) receptors in the brain are involved with thirst, water intake and balance of body liquid. The present study investigated the interaction between Angiotensinergic and GABAergic systems on water intake in adult male rats. Intracerebroventricular (i.c.v.) injections were carried out in all experiments after 24 h deprivation of water intake. After deprivation the volume of consumed water was measured for 1 h. Administration of Losartan (45 µg/rat), Muscimol (0.1 µg/rat) significantly decreased water intake while, i.c.v. microinjection of Bicuculline (1 µg/rat) significantly increased it as compared to Saline-treated controls. I.c.v. microinjection of Muscimol 15 min after Losartan administration decreased water intake significantly, while, i.c.v. microinjection of Bicuculline 15 min after Losartan administration could attenuate increasing effect of Bicuculline on water intake. It is concluded that Angiotensinergic system have interaction with GABAergic system on water intake.
1. Introduction
Thirst is a subjective perception that provides the urge for human and animals to drink fluids. It is important for maintaining body fluid homeostasis and may arise from deficits in either intracellular or extracellular fluid volume [1].
Some studies suggest that various factors are instrumental in causing thirst and these factors can be anatomical and hormonal [1-3]. Anatomical areas like anteroventral region of the third ventricle (AV3V) consists of organum vasculosum lamina terminalis (OVLT), medial preoptic nucleus (MnPO) and anterior preoptic periventricular [1,4] has extensive connections with areas in the brain stem, hypothalamus and limbic system and they also control water intake, sodium appetite and arterial pressure [4,5]. AV3V and subfornical organ (SFO) neurons send some signals to involved areas in thirst like hypothalamus through increasing hormones releasing like Arginine vasopressin (AVP) which, are related to thirst [4,6,7]. Previous studies indicate that the paraventricular nucleus (PVN) is an important source of excitatory drive for sympathetic vasomotor tone [5,8-10].
Furthermore neural signals arising from osmotic and hormonal influences on the lamina terminalis may be integrated within the brain, with afferent information relayed from intrathoracic baroreceptors via the hindbrain to generate thirst [1].
A functional renin-angiotensin system in the brain seems that it has same effects on cardiac contractility, vasoconstriction, vascular hypertrophy, renal blood flow and sodium transport, release of aldosterone and vasopressin, regulation and maintenance of both blood pressure and water as well as the sodium balance of body fluid [3,11-14]. Once released, renin produces Angiotensin I as a cleavage product of angiotensinogen. Angiotensin I is further processed by angiotensin converting enzyme (ACE) into the bioactive Angiotensin II [5,14- 16]. The actions of Angiotensin II occure through binding to cell surface receptors. Two main subtypes of Angiotensin II receptors have been cloned and are termed the type I (AT1) and type II (AT2) receptors [14,16-18]. It is also shown that a number of Ang II sensitive sites located mainly in the anterior hypothalamus [2,19].
The rapid and large volume of water drunk and an increase in blood pressure immediately after an injection of Angiotensin II into the cerebral ventricles or the preoptic region of the brain is a clear indication that central angiotensinergic mechanisms could influence thirst [3,14, 20-22]. Furthermore, Centrally administered Ang II receptor antagonists are known to eliminate the drinking response [3,13,14,23]. The subfornical organ, a circumventricular structure that lacks a functional blood-brain barrier [4,21], is implicated in Angiotensin II-induced drinking and pressor responses [16]. It is likely that AT1 receptors, mainly in the median preoptic nucleus, which is a component of the AV3V region, mediate drinking induced by i.c.v. infusion of Angiotensin II [14,24]. MnPO neurons are stimulated by angiotensinergic projection originating from the SFO and project towards vasopressinergic and oxytocinergic neurons of the PVN for elicitation of drinking behavior [4,25]. When Ang II injected directly into these areas, it is shown an increase in water intake followed by an increase of sodium consumption [4,6,7,14].
GABA is a major inhibitory neurotransmitter in the central nervous system (CNS) of mammalian species with a wide distribution in the brain specially in the hypothalamus [2,26-28]. It is known that there are at least three receptor subtypes, namely, GABAA, GABAB and the more recently discovered GABAC receptors in the anterior hypothalamus or the paraventricular and supraoptic nuclei [28-30]. The GABAA receptor is the main receptor subtype in the CNS, showing predominance over GABAB receptors in most parts of the brain [31, 32].
In conscious rats, i.c.v. treatment with the GABA or Muscimol (a GABAA agonist) suppressed the pressor responses to Ang II in a dose-dependent and reversible fashion [2,3,28,32]. Experimental findings have shown that GABA and its analogs influence the Ang II-induced drinking and pressor responses through the lamina terminalis along the anterior wall of the third ventricle [2, 3,33,34]. It has been demonstrated that the MPO area contains GABA neurons and terminals [34,35]. GABAergic inputs to the MPO are derived from the OVLT. GABAergic projections from the MPO to the hypothalamic regions are involved in drinking behavior [34].
According to GABA and angiotensin receptors in the same areas in brain that are involved with balance of body liquid, [2,36] are scattered, these two systems might have interaction with each other [14,16,37-39] and we wanted to consider the interaction of these systems in water-intake in our experiment.
Studies have shown different effects of GABAergic mechanisms on ingestive behaviors depending on the central area tested [40].
The thing that is crucial is to consider what are the consequences of summing-up the various effects that different areas in brain have in thirst, when we injected these drugs in form of i.c.v. to animals and how they are seen as well.
In the past agonist angiotensinergic system interaction with agonist and antagonist GABAergic system on water intake has been investigated, but so far the interaction of Losartan, antagonist angiotensinergic system with GABAergic system on water-intake has not been considered, and we tested these matters in present research.
2. Materials and Methods
2.1. Animals
Adult male Wistar rats (200 - 250 g) were obtained from the breeding colony of Tarbiat Moallem University of Tehran. Rats were housed three per cage, but one day before test day one per cage, in a temperature (23˚C ± 1˚C) controlled room that was maintained on a 12:12 reversed light cycle (light on at 7:00 a.m.). Rats had unrestricted access to food and water in their home cage. The type of food was pellet and it was purchased from Khorak Dam Pars Co. in Iran.
These animal experiments were carried out in accordance with recommendations from the declaration of Helsinki and the internationally accepted principles for the use of experimental animals.
2.2. Surgical Procedures
The rats were anesthetized with ketamine-xylazine (100 mg/kg ketamine, 5 mg/kg xylazine). The skull was leveled between bregma and lambda. A stainless steel 21- gauge guide cannula (0.8 mm) was implanted above the lateral cerebral ventricle using coordinates from the atlas of Paxinos and Watson at least 5 - 7 days before testing. The coordinates used were 0.8 mm posterior to the bregma, 1.3 mm lateral to the midline and 3.4 mm below the top of the skull. The cannula was fixed to the skull using one screw and dental acrylic.
2.3. Microinjection Procedure
Intracerebroventricular injections were made via guide cannulae with injection needles (27-gauge) that were connected by polyethylene tubing to 10 μl Hamilton microsyringe. The injections (0.5 μl total volume) were delivered over two minutes with a syringe pump, and the injection needles (extending 1.5 mm from the end of the guide cannulae) were left in place an additional minute before they were slowly withdrawn.
2.4. Drugs
The drugs included Losartan potassium (Sigma), an angiotensinergic AT1 receptor antagonist, Muscimol (Sigma), a GABAergic GABAA receptor agonist, Bicuculline (Sigma), a GABAergic GABAA receptor antagonist. Losartan and Muscimol were dissolved in Saline and Bicuculline was dissolved in Propylene glycol. The drugs were used i.c.v. in a volume of 0.5 µl/rat.
2.5. Experimental Procedure
The experiments were performed in conscious freely moving rats 5 - 7 days after brain surgery. 168 adult male rats were divided into 28 groups that each group contained 6 rats. All rats were deprived of water overnight, for 24 h, before each test day and food was available during deprivation but not in test period. The pellet may have a food interaction with thirst, but this condition was similar for all animals, so it has no effect on our results.
After 24 h water deprivation, the drugs were injected i.c.v. over a period of 90s, and water graduated glass cylinders were returned to the cages. Groups with receiving two injections, a control Saline injection followed 15 min later by injection of a drug, or one drug followed 15 min later by another to determine the effect of the first drug on the response to the second. In the control groups with two injections, Saline was injected 15 min before a second administration of Saline. Immediately, after drug administration, water intake was recorded for 1 h by reading from the graduated glass cylinder mounted on the wall of the cages. All experiments did at 9 - 11 o’clock and each rat was tested only once.
The proposal was established and approved by the Research and Animal Ethical Committees of Tarbiat Moallem University, Tehran, Iran.
2.6. Data Analysis
Data are reported as one way ANOVA followed by Tukey or Dunnett to test statistical significance. Differences were considered significant at p < 0.05.
2.7. Histology
Following behavioral testing, animals were sacrificed by decapitation and the brains were removed and fixed in formalin. For histological examination of cannulae and injection placement in the lateral ventricle, 100 μm thick sections were taken and cannulae and injection tracks were examined with light microscopy. Only data obtained from animals whose cannulae and injections were exactly placed in the lateral ventricle were used to analysis.
3. Results
Experiment 1. The effect of i.c.v. injection of AT1 receptor antagonist at different doses on water intake in fluid-deprived rats. Figure 1 shows the effect of i.c.v. injection of Losartan at different doses on water intake in fluid-deprived rats. One way ANOVA analysis indicated that there was a significant decrease in water intake at a dose of 45 µg/rat (p < 0.05) as compared to Salinetreated controls. F (3, 20) = 4.271, (n = 6).
Experiment 2. The effect of i.c.v. injection of GABAA receptor agonist at different does on water intake in fluid-deprived rats. Figure 2 illustrates the effect of i.c.v. injection of Muscimol at different doses on water intake in fluid-deprived rats. One way ANOVA analysis indicated that there was a significant decrease in water intake at a dose of 0.1 µg/rat Muscimol (p < 0.001) as compared to Saline-treated controls. F(3, 20) = 17.591, (n = 6).
Experiment 3: The effect of i.c.v. injection of GABAA receptor antagonist at different doses on water intake in fluid-deprived rats. Figure 3 depicts the effect of i.c.v. injection of Bicuculline at different doses on water intake in fluid-deprived rats. One way ANOVA analysis indicated that there was a significant increase in water intake at a dose of 1 µg/rat Bicuculline (p < 0.01)

Figure 1. The effect of i.c.v. microinjection of Losartan on water intake is shown. Rats were injected with Saline or different doses of Losartan (22.5, 45, 90 µg/rat) and water intake was measured for 1 h. Columns represent the means ± S.E.M. (n = 6). *p < 0.05 Losartan 45 µg/rat vs Saline.

Figure 2. The effect of i.c.v. microinjection of Muscimol on water intake is shown. Rats were injected with Saline or different doses of Muscimol (0.05, 0.1, 0.2 µg/rat) and water intake was measured for 1 h. Columns represent the means ± S.E.M. (n = 6). ***p < 0.001 Muscimol 0.1 µg/rat vs Saline.
as compared to Saline-treated controls. F(3, 20) = 11.922, (n = 6).
Experiment 4: The effect of i.c.v interaction between AT1 receptor antagonist and GABAA receptor agonist on water intake in fluid-deprived rats. Figure 4 illustrates the effect of i.c.v. interaction between Losartan and Muscimol on water intake in fluid-deprived rats. One-way ANOVA analysis for i.c.v. injection of Losartan and Muscimol alone or together indicated that a significant decrease at a dose of 0.1 µg/rat Muscimol (p < 0.05) and Los/Mus (p < 0.01) on water intake as compared to Saline-treated controls. I.c.v. microinjection of Muscimol 15 min after Losartan administration (p < 0.01) could elevate the inhibitory effect of Losartan on water intake significantly. F(3, 20) = 5.682, (n = 6).
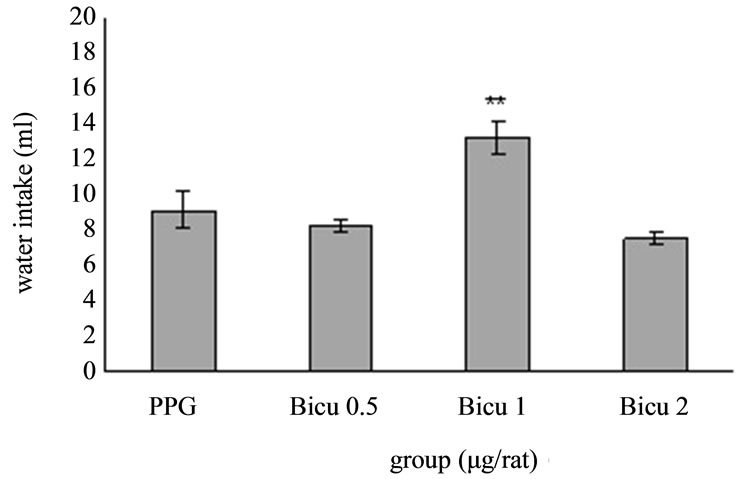
Figure 3. The effect of i.c.v. microinjection of Bicuculline on water intake is shown. Rats were injected with propylene glycol or different doses of Bicuculline (0.5, 1.2 µg/rat) and water intake was measured for 1 h. Columns represent the means ± S.E.M. (n = 6). **p < 0.01 Bicuculline 1 µg/rat vs propylene glycol.
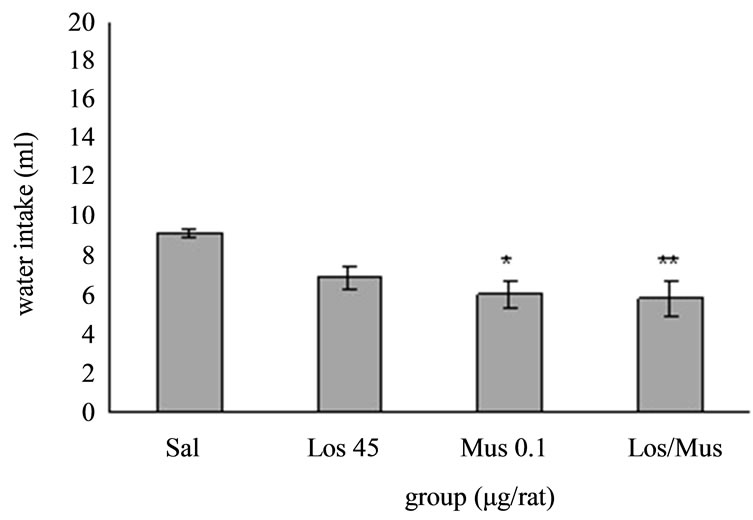
Figure 4. The effect of i.c.v. interaction between Losartan and Muscimol on water intake is shown. Rats were injected with Losartan (45 µg/rat) and Muscimol (0.1 µg/rat) alone. Muscimol was administered 15 min after injection of Losartan. Water intake was measured for 1 h. Columns represent the means ± S.E.M. (n = 6). *p < 0.05 Muscimol 0.1 µg/rat vs Saline, **p < 0.01 Los/Mus vs Saline.
Experiment 5: The effect of i.c.v. interaction between AT1 receptor antagonist and GABAA receptor antagonist on water intake in fluid-deprived rats. Figure 5 depicts the effect of i.c.v. interaction between Losartan and Bicuculline on water intake in fluid-deprived rats. One-way ANOVA analysis for i.c.v. injections of Losartan and Bicuculline alone and together indicated that there was a significant increase at a dose of 1 µg/rat Bicuculline (p < 0.01), on water intake as compared to Propylene glycol-treated controls. I.c.v. microinjection of Bicuculline 15 min after Losartan administration could attenuate the inhibitory effect of Losartan, however this decrease was not significant. F(3, 20) = 12.364, (n = 6).
Experiment 6: The effect of i.c.v. interation between Saline and Propylene glycol on water intake in fluid-deprived rats. Figure 6 depicts the effect of i.c.v. interaction between Saline and Propylene glycol on water intake in fluid-deprived rats. One-way ANOVA analysis for i.c.v. injections of Saline and Propylene glycol alone and together indicated that i.c.v. microinjection of Propylene glycol 15 min after Saline administration there was no significant effect on water intake as compared to Saline-treated controls. F(3, 20) = 0.7577, (n = 6).
4. Discussion
Our results showed that i.c.v. microinjection of Losartan (45 µg/rat) and Muscimol (0.1 µg/rat) significantly decreased water intake in water-deprived rats as compared to saline treated normohydrated controls while Bicuculline (1 µg/rat) increased. It was also shown i.c.v. microinjection of Muscimol (0.1 µg/rat) 15 min after Losartan (45 µg/rat) decreased water intake significantly,
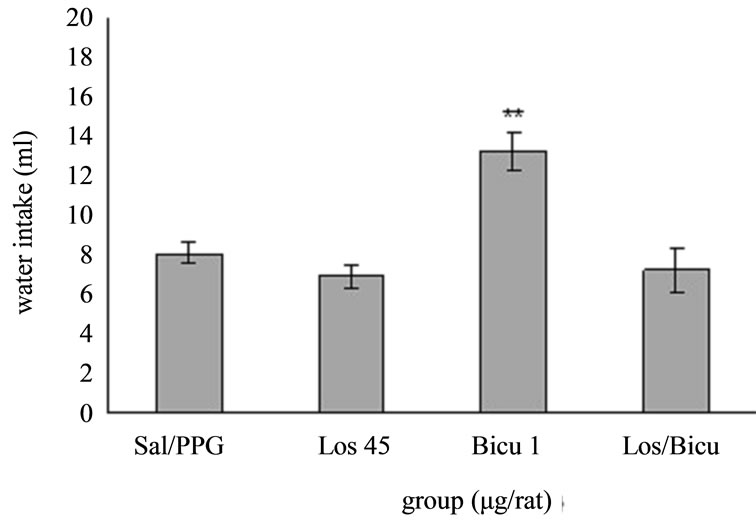
Figure 5. The effect of i.c.v. interaction between Losartan and Bicuculline on water intake is shown. Rats were injected with Losartan (45 µg/rat) and Bicuculline (1 µg/rat) alone. Bicuculline was administered 15 min after injection of Losartan. Water intake was measured for 1h. Columns represent the means ± S.E.M. (n = 6). **p < 0.01 Bicuculline 1 µg/rat vs propylene glycol.

Figure 6. The effect of i.c.v. interaction between Saline and propylene glycol on water intake is shown. Rats were injected with Saline and propylene glycol alone, propylene glycol was administered 15 min after injection of Saline. Water intake was measured for 1 h. Columns represent the means ± S.E.M. (n = 6).
while i.c.v. pretreatment with Losartan 15 min before injection of Bicuculline have no significant effect on water-intake as compared to saline-treated normohy-drated controls.
A functional renin-angiotensin system in the brain seems to play a major role in the regulation and maintenance of both blood pressure and water as well as sodium in the body fluid [3].
It has been observed that Losartan has an inhibitory effect on renin-angiotensin system and causes decrease of water intake, blood pressure, Na+ intake and increase of Na+ excretion and imbalance of body fluids [14,21, 22,41].
AT1 receptors affect water intake [16]. There are a high density of AT1 receptors in the subfornical organ, OVLT, median eminence, and area postrema [13,14]. The blood-born Ang II acts both as a circulating signal through receptors in the circumventricular organs and as a neurotransmitter in several areas of the hypothalamus and medulla [5]. It has been indicated that these areas play a major role in water intake and the balance of body fluids [14,16], so Losartan as AT1 receptor antagonist could decreases water intake.
Alternatively, it is possible that the likely antagonism by Losartan of the pressor action of peripheral Ang II could have diminished the access of Ang II itself to the SFO [21] and as a result induces water intake decreasing.
Pathways from AV3V area to the PVN appear to be a major link in sympathoadrenal nervous system activation [42-44]. The descending pathways from the PVN increase blood pressure through increasing of Epinephrine, Norepinephrine and Aldosteron [44,45]. It seems that Losartan could block these excitatory impulses and also it has an inhibitory effect on sympathoadrenal system and therefore falls blood pressure.
Hypovolemia, Ang II, aldosteron and antidiuretic hormone (ADH) increase blood pressure and stimulate volume receptors and baroreceptors and make inhibitory impulses to the thirst centers decrease and so water intake increases [13]. Cardiopulmonary baroreceptors stimulation plays an important role in drinking behavior because the PVN receives baroreceptor input [21]. The circulating Ang II can influence the excitability of PVN neurons through synaptic connections with circumventricular organs that lack a normal blood-brain barrier [5]. The supraoptic nucleus (SON) and PVN nuclei to respond to i.c.v. injections of Ang II with an increase of a neuronal firing pattern typical for AVP release [2,46]. I.c.v. microinjection of Losartan can access to these nuclei and causes drinking inhibition by effect on recaptors and decreased AVP. Also it could block AT1 receptors in circumventricular organ [2,13,21], therefore excitatory impulse can’t be sent to PVN, as a result the release of AVP and water intake will be decreased.
ADH (or AVP) may change the threshold to the onest of drinking in response to cellular dehydration and other thirst stimuli [13].
The vasopressine are made up of three receptor subunits: V1a, V1b and V2 [47-49]. The V1b receptor is known to stimulate the release of adrenocorticotropin hormone, which stimulates the release of aldosterone hormone that result in increasing Na+ reabsorption, blood pressure and water intake [48,50]. The V2 receptor which is in kidneys has critical role to fluid homeostasis [49,51].
It seems hypovolemia and/or sodium depletion or intracranial Ang II induced highly localized expression of c-Fos in areas known to be involved in Ang II-induced drinking, including SFO, OVLT, as well as in MnPO and PVN nuclei [5,13]. Fos-immunoreactivity (Fos-ir) may be caused at least in part by circulating Ang II reaching the SFO or other brain regions involved in thirst lack a tight blood-brain barrier [13,21]. Water intake is stimulated due to Fos expression in these areas.
Injection of Losartan blocked Angiotensinergic system through AT1 receptors [14,21] and also prevents induction of Fos-ir and as a result of that causes water intake decrease [13].
According to above reasons, Losartan significantly decreased water intake in the water-deprived rats as compared to saline treated normohydrated controls.
In the second experiment was shown that GABA and Muscimol could reduce water intake. The GABA exerted its inhibitory action on a circumventricular organ, most likely the paraventricular nucleus [2,36]. So this matter reveals that stimulation of GABAA receptors in these areas considered as an inhibitory arousal but these effects are not seen in GABAB receptors [34]. This inhibitory effect is reversed by pretreatment with the GABAA receptor antagonist Bicuculline [32]. GABAergic stimulation approaches membrane potential to resting level [53]. So causes inhibitory of Angiotensinergic and Vasopersinergic neurons stimulation.
It is shown that circumventricular organ have inhibitory projection to MPO nucleus [34]. GABAergic projections from the MPO also inhibit the excitability of both vasopressinand oxytocin-secreting cells in the PVN and SON [34,54] and consequently cause AVP release and water-intake decrease.
When rats became deprived from water for 24 hours, the amount of Angiotensin II rises in them due to lack of water and body fluid imbalance, so animal desires to drink water while Muscimol injection could inhibit this process [2,32]. Some of researchers suggested that i.c.v. injection of Muscimol could induce a fall in blood pressure [44,55-57] by 2 ways: 1) prevention of Na+ reabsorption that it is caused to decrease water intake and blood pressure [2] ; 2) Muscimol could stimulate the inhibitory GABAergic function in PVN that it could decrease AVP release, water intake [44,57] and also exert a tonic inhibitory effect on sympathoadrenal system activity, as a result of blood pressure fall [44,57-59].
Inhibition of GABAA receptors by Bicuculline also elicits an increase in sympathetic outflow and blood pressure [44,57,60-62] and stimulates baroreceptors, as a result water intake increases.
In the 4 and 5 experiments have been shown that i.c.v. injection of Muscimol 15 min after losartan administration decreased water intake significantly, while i.c.v. injection with Losartan 15 min before injection of Bicuculline have no significant effect on water intake.
Unger et al. showed that stimulation of GABAergic receptors in the brain inhibited all the central actions of Ang II investigated: pressor effect, drinking responses and release of AVP from the pituitary gland [3,40]. Also they indicated that the GABA interactions with central angiotensin pressor pathways are specific. GABAergic stimulation has less or little effect on other peptidergic pressor responses [2,33].
The previous information showed that excitation of Ang system increases AVP release [3,63]. The suppression of AVP release by GABAergic stimulation may be responsible for at least part of its reduction of the pressor responses to i.c.v. Ang II [2,64].
Some of findings have clearly shown that the MPO is an important site for the GABAergic control of the dipsogenic action produced by Ang II [34,35]. GABAergic synaptic input tonically inhibits the firing activity of PVN presympathetic neurons [8,10,65]. Ang II activates presynaptic AT1 receptors to increase the firing of PVN outputs neurons through inhibition of GABA release (disinhibition) [66,67]. Ang II attenuates GABAergic input to PVN presynaptic neurons by reactivated oxygen species (ROS), especially superoxide anions [5,68] through inhibition of synaptic synaptosomal-associated protein 25 (SNAP25) on the presynaptic terminal [69]. Ang II in PVN neurons produces ROS that it can inhibit synaptic GABA release [5,70]. Activation of AT1 receptors by Ang II causes activation Gi/o proteins and stimulation of NADPH oxidase [71]. Gi/o proteins contribute to presynaptic inhibition of GABA release to PVN pre-sympathetic neurons by Ang II [5].
To agree with above literature, the present results are fully depicting the fact. According to increasing effect of Bicuculline on water intake, i.c.v. injection of Bicuculline 15 min after Losartan administration could attenuate the inhibitory effect of Losartan on water intake.
In other words, i.c.v. pretreatment with Losartan 15 min before injection of Bicuclline could attenuate increasing effect of Bicuculline on water intake.
The present data indicated that Angiotensinergic and GABAergic systems have a close interaction in the water intake mechanisms, but clearly further studies are needed to understand better how these systems contribute together.
5. Acknowledgements
This work was granted by Pasteur Institute of Iran and Tarbiat Moallem University.
REFERENCES
- M. J. McKinley and A. K. Johnson, “The Physiological Regulation of Thirst and Fluid Intake,” News in Physiological Sciences, Vol. 19, No. 1, 2004, pp. 1-6. doi:10.1152/nips.01470.2003
- T. Unger, F. Bles, D. Ganten, R. E. Lang, R. Rettig and N. A. Schwab, “GABAergic Stimulation Inhibits Central Actions of Angiotensin II: Pressor Responses, Drinking and Release of Vasopressin,” European Journal of Pharmacology, Vol. 90, No. 1, 1983, pp. 1-9. doi:10.1016/0014-2999(83)90207-8
- M. Abe, T. Tokunaga, K. Yamada and T. Furukawa, “Gamma-Aminobutyric Acid and Taurine Antagonize the Central Effects of Angiotensin II and Renin on the Intake of Water and Salt, and on Blood Pressure in Rats,” Neuropharmacology, Vol. 27, No. 3, 1988, pp. 309-318. doi:10.1016/0028-3908(88)90049-4
- L. J. Waldecy and R. F. Celso, “Angiotensinergic Pathway through the Median Preoptic Nucleus in the Control of Oxytocin Secretion and Water and Sodium Intake,” Brain Research, Vol. 1014, No. 1-2, 2004, pp. 236-243. doi.: 10.1016/j.brainres.2004.03.077
- Q. Chen and H. L. Pan, “Signaling Mechanisms of Angiotensin II—Induced Attenuation of GABAergic Input to Hypothalamic Presympathetic Neurons,” Journal of Neurophysiology, Vol. 97, No. 5, 2007, pp. 3279-3287. doi:10.1152/jn.01329.2006
- D. A. Fitts and D. B. Masson, “Preoptic Angiotensin and Salt Appetite,” Behavioral Neuroscience, Vol. 104, No. 4, 1990, pp. 643-650. doi:10.1037/0735-7044.104.4.643
- K. Honda, H. Aradachi, T. Higuchi, S. Takano and H. Negoro, “Activation of Paraventricular Neurosecretory Cells by Local Osmotic Stimulation of the Median Preoptic Nucleus,” Brain Research, Vol. 594, No. 2, 1992, pp. 335-338. doi:10.1016/0006-8993(92)91147-7
- D. S. Martin and J. R. Haywood, “Hemodynamic Responses to Paraventricular Nucleus Disinhibition with Bicuculline in Conscious Rats,” American Journal of Physiology, Vol. 265, No. 5, 1993, pp. H1727-H1733.
- J. H. Coote, Z. Yang, S. Pyner and J. Deering, “Control of Sympathetic Outflows by the Hypothalamic Paraventricular Nucleus,” Clinical and Experimental, Vol. 25, No. 6, 1998, pp. 461-463. doi:10.1111/j.1440-1681.1998.tb02235.x
- A. M. Allen, “Inhibition of the Hypothalamic Paraventricular Nucleus in Spontaneously Hypertensive Rats Dramatically Reduces Sympathetic Vasomotor Tone,” Hypertension, Vol. 39, No. 2, 2002, pp. 275-280. doi:10.1161/hy0202.104272
- E. S. Halperin, J. Y. Summy-Long, L. C. Keil and W. B. Severs, “Aspects of Salt/Water Balance after Cerebroventricular Infusion of Angiotensin II,” Brain Research, Vol. 205, No.1, 1981, pp. 219-221. doi:10.1016/0006-8993(81)90736-8
- T. Unger, O. Chung, T. Csikos, J. Culman, S. Gallinat, P. Gohlke, S. Höhle, S. Meffert, M. Stoll, U. Stroth and Y.-Z. Zhu, “Angiotensin Receptors,” The Journal of Hypertension, Vol. 14, No. 5, 1996, pp. S95-S103.
- J. T. Fitzsimons, “Angiotensin, Thirst, and Sodium Appetite,” Physiological Reviews, Vol. 78, No. 3, 1998, pp. 583-686.
- M. J. Mckinley, A. M. Allen, M. L. Mathal, C. May, R. M. Mcallen, B. J. Oldfield and R. S. Weisinger, “Brain Angiotensin and Body Fluid Homeostasis,” The Japanese Journal of Physiology, Vol. 51, No. 3, 2001, pp. 281-289. doi:10.2170/jjphysiol.51.281
- K. J. Catt, M. C. Carson, W. P. Hausdorff, C. M. LeachHarper, A. J. Baukal, G. Guillemette, T. Balla and G. Aguilera, “Angiotensin II Receptors and Mechanisms of Action in Adrenal Glomerulosa Cells,” Journal of Steroid Biochemistry, Vol. 27, No. 4-6, 1987, pp. 915-927. doi:10.1016/0022-4731(87)90168-3
- D. Daniels, D. K. Yee and S. J. Fluharty, “Angiotensin II Receptor Signaling,” Experimental Physiology, Vol. 92, 2007, pp. 523-527. doi:10.1113/expphysiol.2006.036897
- T. J. Murphy, R. W. Alexander, K. K. Griendling, M. S. Runge and K. E. Bernstein, “Isolation of a cDNA Encoding the Vascular Type-1 Angiotensin II Receptor,” Nature, Vol. 351, No. 6323, 1991, pp. 233-236. doi:10.1038/351233a0
- Y. Kambayashi, S. Bardhan, K. Takahashi, S. Tsuzuki, H. Inui, T. Hamakubo and T. Inagami, “Molecular Cloning of a Novel Angiotensin II Receptor Isoform Involved in Phosphotyrosine Phosphatase Inhibition,” The Journal of Biological Chemistry, Vol. 268, No. 33, 1993, pp. 24543- 24546.
- R. E. Lang, T. Unger, W. Rascher and D. Ganten, “Brain Angiotensin,” In: L. L. Iversen, Ed., Handbook of Psychopharmacology, Plenum Publishing Corp, New York, 1982, p. 307.
- J. T. Fitzsimons, “Angiotensin Stimulation of the Central Nervous System,” Reviews of Physiology, Biochemistry and Pharmacology, Vol. 87, 1980, pp. 117-167. doi:10.1007/BFb0030897
- E. C. Crews and N. E. Rowland, “Role of Angiotensin in Body Fluid Homeostasis of Mice: Effect of Losartan on Water and NaCl Intakes,” American Journal of Physiology, Vol. 288, No. 3, 2005, pp. R638-R644.
- K. Sakai, K. Agassandian, S. Morimoto, P. Sinnayah, M. D. Cassell, R. L. Davisson and C. D. Sigmund, “Local Production of Angiotensin II in the Subfornical Organ Causes Elevated Drinking,” The Journal of Clinical Investigation, Vol. 117, No. 4, 2007, pp. 1088-1095. doi:10.1172/JCI31242
- P. C. Wong, W. A. Price, A. T. Chiu, J. V. Duncia, D. J. Carin, R. R. Wexler, A. L. Johnson and P. B. M. W. M. Timmermans, “Nonpeptide Angiotensin II Receptor Antagonists. VIII. Characterization of Functional Antagonism Displayed by DuP 753: An Orally Active Antihypertensive Agent,” The Journal of Pharmacology and Experimental Therapeutics, Vol. 252, No. 2, 1990, pp. 719-725.
- T. P. O’Neill and M. J. Brody, “Role for the Median Preoptic Nucleus in Centrally Evoked Pressor Responses,” The American Journal of Physiology, Vol. 252, No. 6, 1987, pp. R1165-R1172.
- M. Kadekaro, J. Y. S. Long, S. Freeman, J. S. Harris and M. L. Terrell, “Cerebral Metabolic Responses and Vasopressin and Oxytocin Secretion during Progressive Water Deprivation in Rat,” American Journal of Physiology, Vol. 262, No. 2, 1992, pp. 310-317.
- M. P. Meeley, M. D. Underwood, W. T. Talman and D. J. Reis, “Content and in Vitro Release of Endogenous Amino Acids in the Area of the Solitary Tract of the Rat,” The Journal of Neurochemistry, Vol. 53, No. 6, 1989, pp. 1807-1817. doi:10.1111/j.1471-4159.1989.tb09247.x
- T. Araki, H. Kiyama and M. Tohyama, “The GABAA Receptor Gamma 1 Subunit Is Expressed by Distinct Neuronal Populations,” Molecular Brain Research, Vol. 15, No. 2, 1992, pp. 121-132. doi:10.1016/0169-328X(92)90159-9
- J. C. Callera, L. B. Oliveira, S. P. Barbosa, D. S. A. Colombari, L. A. Deluca and J. V. Menani, “GABAA Receptor Activation in the Lateral Parabrachial Nucleus Induces Water and Hypertonic NaCl Intake,” Neuroscience, Vol. 134, No. 3, 2005, pp. 725-735. doi:10.1016/j.neuroscience.2005.05.009
- N. G. Bowery, A. L. Hudson and G. W. Price, “GABAA and GABAB Receptor Binding Site Distribution in the Rat Central Nervous System,” Neuroscience, Vol. 20, No. 2, 1987, pp. 365-383. doi:10.1016/0306-4522(87)90098-4
- N. G. Bowery, “GABAB Receptors and Their Significance in Mammalian Pharmacology,” Trends in Pharmacological Sciences, Vol. 10, No. 10, 1989, pp. 401-407. doi:10.1016/0165-6147(89)90188-0
- D. C. M. Chu, R. L. Albin, A. B. Young and J. B. Penny, “Distribution and Kinetics of GABAB Receptor Binding Sites in the Central Nervous System: A Quantitative Autoradiographic Study,” Neuroscience, Vol. 34, No. 2, 1990, pp. 341-357. doi:10.1016/0306-4522(90)90144-S
- A. J. Houston, J. C. Wong and I. S. Ebenezer, “Effect of Subcutaneous Administration of the Gamma-Aminobutyric Acid: A Receptor Agonist Muscimol on Water Intake in Water-Deprived Rats,” Physiology and Behavior, Vol. 77, No. 2, 2002, pp. 445-450.
- D. L. Jones and G. J. Mogenson, “Central Injections of Spiperone and GABA: Attenuation of Angiotensin II Stimulated Thirst,” Canadian Journal of Physiology and Pharmacology, Vol. 60, No. 5, 1982, pp. 720-726. doi:10.1139/y82-098
- J. Tanaka, S. Fujisawa and M. Nomura, “GABAergic Modulation of the Ang II-Induced Drinking Response in the Rat Medial Preoptic Nucleus,” Pharmacology, Biochemistry and Behavior, Vol. 76, No. 1, 2003, pp. 43-51. doi:10.1016/S0091-3057(03)00195-3
- E. Mugnaini and W. H. Oertel, “An Atlas of the Distribution of GABAergic Neurons and Terminals in the Rat CNS as Revealed by GAD Immunocytochemistry,” Handbook of Chemical Neuroanatomy 4, Elsevier, New York, 1985, pp. 436-608.
- W. Feldberg and M. S. E. Rocha, “Inhibition of Vasopressin Release to Carotid Occlusion by Gamma-Aminobutyric Acid and Glycine,” British Journal of Pharmacology, Vol. 72, No. 1, 1981, pp. 17-24.
- F. A. Mendelsohn, R. Quirion, J. M. Saavedra, G. Aguilera and K. J. Catt, “Autoradiographic Localization of Angiotensin II Receptors in Rat Brain,” Proceedings of the National Academy of Sciences of the USA, Vol. 81, No. 5, 1984, pp. 1575-1579. doi:10.1073/pnas.81.5.1575
- K. Song, A. M. Allen, G. Paxinos and F. A. Mendelsohn, “Mapping of Angiotensin II Receptor Subtype Heterogeneity in Rat Brain,” The Journal of Comparative Neurology, Vol. 316, No. 4, 1992, pp. 467-484. doi:10.1002/cne.903160407
- M. E. Giles, R. T. Fernley, Y. Nakamura, I. Moeller, G. P. Aldred, T. Ferraro, J. D. Penschow, M. J. McKinley and B. J. Oldfield, “Characterization of a Specific Antibody to the Rat Angiotensin II AT1 Receptor,” The Journal of Histochemistry and Cytochemistry, Vol. 47, No. 4, 1999, pp. 507-516. doi:10.1177/002215549904700409
- L. B. de Oliveira, J. C. Callera, L. A. de Luca Jr., D. S. A. Colombari and J. V. Menani, “GABAergic Mechanisms of the Lateral Parabrachial Nucleus on Sodium Appetite,” Brain Research Bulletin, Vol. 73, No. 2, 2007, pp. 238- 247. doi:10.1016/j.brainresbull.2007.03.006
- R. DiNicolantonio, “Angiotensin Converting Enzyme Blockade and Thirst,” Clinical and Experimental Hypertension, Part A, Vol. 6, No. 10-11, 1984, pp. 2025-2029. doi:10.3109/10641968409046121
- A. Goto, T. Ikeda, L. Tobian, J. Iwai and M. A. Johnson, “Brain Lesions in the Paraventricular Nuclei and Catecholaminergic Neurons Minimize Salt Hypertension in Dahl Salt-Sensitive Rats,” Clinical Science, Vol. 61, No. 7, 1981, pp. 53S-55S.
- T. C. Herzig, R. A. Buchholz and J. R. Haywood, “Effects of Paraventricular Nucleus Lesions on Chronic Renal Hypertension,” American Journal of Physiology, Vol. 261, No. 3, 1991, pp. H860-H867.
- J. R. Haywood, S. W. Mifflin, T. Craig, A. Calderon, J. G. Hensler and C. Hinojosa-Laborde, “Gamma-Aminobutyric Acid (GABA)—A Function and Binding in the Paraventricular Nucleus of the Hypothalamus in Chronic Renal-Wrap Hypertension,” Hypertension, Vol. 37, No. 2, 2001, pp. 614-618.
- R. N. Ranson, K. Motawei, S. Pyner and J. H. Coote, “The Paraventricular Nucleus of the Hypothalamus Sends Efferents to the Spinal Cord of the Rat That Closely Appose Sympathetic Preganglionic Neurons Projecting to the Stellate Ganglion,” Experimental Brain Research, Vol. 120, No. 2, 1998, pp. 164-172. doi:10.1007/s002210050390
- T. Akaishi, H. Negoro and S. Kobayasi, “Responses of Paraventricular and Supraoptic Units to Angiotensin II, Sar-Ile8-Angiotensin II and Hypertonic NaCl Administered into the Cerebral Ventricle,” Brain Research, Vol. 188, No. 2, 1980, pp. 499-511. doi:10.1016/0006-8993(80)90048-7
- M. Thibonnier, C. Auzan, Z. Madhun, P. Wilkins, L. Berti-Mattera and E. Clauser, “Molecular Cloning, Sequencing, and Functional Expression of a cDNA Encoding the Human V1a Vasopressin Receptor,” The Journal of Biological Chemistry, Vol. 269, No. 5, 1994, pp. 3304-3310.
- M. Birnbaumer, “Vasopressin Receptors,” Trends in Endocrinology and Metabolism, Vol. 11, No. 10, 2000, pp. 406-410. doi:10.1016/S1043-2760(00)00304-0
- J. Guan, C. Mao, X. Feng, H. Zhang, F. Xu, C. Geng, L. Zhu, A. Wang and Z. Xu, “Fetal Development of Regulatory Mechanisms for Body Fluid Homeostasis,” Brazilian Journal of Medical and Biological Research, Vol. 41, No. 6, 2008, pp. 446-454. doi:10.1590/S0100-879X2008005000025
- J. C. Geerling and A. D. Loewy, “Central Regulation of Sodium Appetite,” Experimental Physiology, Vol. 93, No. 2, 2008, pp. 177-209. doi:10.1113/expphysiol.2007.039891
- M. Birnbaumer, “Vasopressin Receptor Mutations and Nephrogenic Diabetes Insipidus,” Archives of Medical Research, Vol. 30, No. 6, 1999, pp. 465-474. doi:10.1016/S0188-4409(99)00063-6
- J. Herbert, M. L. Forsling, S. R. Howes, P. M. Stacey and H. M. Shiers, “Regional Expression of c-fos Antigen in the Basal Forebrain Following Intraventricular Infusions of Angiotensin and Its Modulation by Drinking Either Water or Saline,” Neuroscience, Vol. 51, No. 4, 1992, pp. 867-882. doi:10.1016/0306-4522(92)90526-8
- E. Roberts, “Living Systems Are Tonically Inhibited, Autonomous Optimizers, and Disinhibition Coupled to Variability Generation Is Their Major Organizing Principle: Inhibitory Command-Control at Levels of Membrane, Genome, Metabolism, Brain, and Society,” Neurochemical Research, Vol. 16, No. 3, 1991, pp. 409-421. doi:10.1007/BF00966104
- R. Nissen and L. P. Renaud, “GABA Receptor Mediation of Median Preoptic Nucleus-Evoked Inhibition of Supraoptic Neurosecretory Neurons in Rat,” The Journal of Physiology, Vol. 479, 1994, pp. 207-216.
- M. J. Antonaccio and D. W. Snyder, “Reductions in Blood Pressure, Heart Rate and Renal Sympathetic Nervous Discharge after Imidazole-4-Acetic Acid: Mediation through Central γ-Aminobutyric Acid (GABA) Receptor Stimulation,” The Journal of Pharmacology and Experimental Therapeutics, Vol. 218, No. 1, 1981, pp. 200-205.
- G. K. Matheson, E. Freed and G. Tunnicliff, “Novel GABA Analogues as Hypotensive Agents,” Neuropharmacology, Vol. 25, No. 11, 1986, pp. 1191-1195. doi:10.1016/0028-3908(86)90135-8
- D. S. Martin and J. R. Haywood, “Reduced GABA Inhibition of Sympathetic Function in Renal-Wrapped Hypertensive Rats,” The American Journal of Physiology, Vol. 275, No. 5, 1998, pp. R1523-R1529.
- T. Unger, H. Becker, R. Dietz, D. Ganten, R. E. Lang, R. Rettig, A. Schomig and N. A. Schwab, “Antihypertensive Effect of the GABA Receptor Agonist Muscimol in Spontaneously Hypertensive Rats,” Circulation Research, Vol. 54, No. 1, 1984, pp. 30-37.
- S. Nagahama, R. Dawson and S. Oparil, “Enhanced Depressor Effect of Muscimol in the DOCA/NaCl Hypertensive Rat: Evidence for Altered GABAergic Activity in Brain,” Proceedings of the Society for Experimental Biology and Medicine, Vol. 180, No. 2, 1985, pp. 277-283.
- D. S. Martin, T. Segura and J. R. Haywood, “Cardiovascular Responses to Bicuculline in the Paraventricular Nucleus of the Rat,” Hypertension, Vol. 18, No. 1, 1991, pp. 48-55.
- J. R. Haselton, J. Goering and K. P. Patel, “Parvocellular neurons of the Paraventricular Nucleus Are Involved in the Reduction in Renal Nerve Discharge during Isotonic Volume Expansion,” The Journal of the Autonomic Nervous System, Vol. 50, No. 1, 1994, pp. 1-11. doi:10.1016/0165-1838(94)90117-1
- K. Zhang and K. P. Patel, “Effect of Nitric Oxide within the Paraventricular Nucleus on Renal Sympathetic Nerve Discharge: Role of GABA,” The American Journal of Physiology, Vol. 275, No. 3, 1998, pp. R728-R734.
- W. B. Severs and A. E. Daniels-Severs, “Effects of Angiotensin on the Central Nervous System,” Pharmacological Reviews, Vol. 25, No. 3, 1973, pp. 415-449.
- T. Unger, W. Rascher, C. Schuster, R. Pavlovitch, A. Schomig, R. Dietz and D. Ganten, “Central Blood Pressure Effects of Substance P and Angiotensin II: Role of the Sympathetic Nervous System and Vasopressin,” European Journal of Pharmacology, Vol. 71, No. 1, 1981, pp. 33-42. doi:10.1016/0014-2999(81)90384-8
- D. P. Li and H. L. Pan, “Role γ-Aminobutyric Acid (GABA)A and GABAB Receptors in Paraventricular Nucleus in Control of Sympathetic Vasomotor Tone in Hypertension,” The Journal of Pharmacology and Experimental Therapeutics, Vol. 320, No. 2, 2007, pp. 615-626. doi:10.1124/jpet.106.109538
- D. P. Li, S. R. Chen and H. L. Pan, “Angiotensin II Stimulates Spinally Projecting Paraventricular Neurons through Presynaptic Disinhibition,” The Journal of Neuroscience, Vol. 23, No. 12, 2003, pp. 5041-5049.
- D. P. Li and H. L. Pan, “Angiotensin II Attenuates Synaptic GABA Release and Excites Paraventricular-Rostral Ventrolateral Medulla Output Neurons,” The Journal of Pharmacology and Experimental Therapeutics, Vol. 313, No. 3, 2005, pp. 1035-1045. doi:10.1124/jpet.104.082495
- B. Erdos, C. S. Broxson, M. A. King, P. J. Scarpace and N. Tumer, “Acute Pressor Effect of Central Angiotensin II Is Mediated by NAD(P)H-Oxidase-Dependent Production of Superoxide in the Hypothalamic Cardiovascular Regulatory Nuclei,” The Journal of Hypertension, Vol. 24, No. 1, 2006, pp. 109-116. doi:10.1097/01.hjh.0000198026.99600.59
- A. R. Giniatullin, F. Darios, A. Shakirzyanova, B. Davletov and R. Giniatullin, “SNAP25 Is a Pre-Synaptic Target for the Depressant Action of Reactive Oxygen Species on Transmitter Release,” The Journal of Neurochemistry, Vol. 98, No. 6, 2006, pp. 1789-1797. doi:10.1111/j.1471-4159.2006.03997.x
- M. V. Avshalumov, B. T. Chen and M. E. Rice, “Mechanisms Underlying H2O-Mediated Inhibition of Synaptic Transmission in Rat Hippocampal Slices,” Brain Research, Vol. 882, No. 1, 2000, pp. 86-94. doi:10.1016/S0006-8993(00)02835-3
- Y. Groemping, K. Lapouge, S. J. Smerdon and K. Rittinger, “Molecular Basis of Phosphorylation-Induced Activation of the NADPH Oxidase,” Cell, Vol. 113, No. 3, 2003, pp. 343-355. doi:10.1016/S0092-8674(03)00314-3
NOTES
*Corresponding author.

