Journal of Transportation Technologies
Vol.04 No.04(2014), Article ID:50741,9 pages
10.4236/jtts.2014.44029
A De-Noising Method for Track State Detection Signal Based on the Statistical Characteristic of Noise
Liming Li, Xiaodong Chai, Shubin Zheng, Wenfa Zhu
College of Urban Railway Transportation, Shanghai University of Engineering Science, Shanghai, China
Email: liming0028@126.com, cxdyj@163.com, zhengshubin@126.com, zhuwenfa1986@163.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 1 August 2014; revised 26 August 2014; accepted 17 September 2014
ABSTRACT
Based on the statistical characteristics analysis of random noise power and autocorrelation function, this paper proposes a de-noising method for track state detection signal by using Empirical Mode Decomposition (EMD). This method is used to noise reduction refactoring for the first Intrinsic Mode Function (IMF) component in accordance with the “random sort-accumulation-aver- age-refactoring" order. Signal autocorrelation function characteristics are used to determine the cut-off point of the dominant mode. This method was applied to test signals and the actual inertial unit signals; the experimental results show that the method can effectively remove the noise and better meet the precision requirement.
Keywords:
Track Inspection, Long Wave Irregularity, Empirical Mode Decomposition, De-Noising

1. Introduction
Tracks are the infrastructure to train safe operation due to the uneven elasticity of track structure and rail base can cause rail line long wave irregularities [1] [2] . Inertia method is the main technical route in track detection [3] - [6] . Using strapdown inertial technology test track long-wave rough chronological, due to the inertia unit acceleration signal collected contain more low frequency noise, easy to cause integrator saturation, so we must do de-noising processing first before the integral on acceleration signal.
The complex signal can be decomposed into level signals step by step (i.e., to smooth the signal processing) based on the empirical mode decomposition according to different time scales and get a series of intrinsic mode function characteristics of different scales. Each IMF component contains a signal from low frequency to high frequency of different ingredients and each frequency component that is included in the frequency changes over the signal itself [7] [8] . So the EMD can be thought of as a space-time filtering process based on signal extremum characteristic scale. This property is used in signal filtering analysis and noise reduction processing. In this paper, through the statistical characteristics analysis of random noise power and autocorrelation function, we put forward the EMD de-noising method based on noise statistical characteristics. Experimental results show that the method can effectively suppress noise and improve the track irregularity detection accuracy.
2. The Principle of Inertial Reference Method Detection
Inertial reference method [9] [10] measuring system is in the moving car, speed meter and gyroscope is used to establish an inertial reference benchmark, through the measurements of these two kinds of inertial components analytical method to get a benchmark, and reuse displacement sensor or image sensor measurement orbit relative position relative to the benchmark, and get the relative position at the top of the rail in the inertial coordinate system.
As shown in Figure 1, under the same datum point, according to the basic principle of strap down inertial navigation system [11] [12] , using the angular velocity signal output by gyroscope, real-time updating the attitude matrix of the carrier, through the attitude matrix we can transform the acceleration signal output from accelerometer into the geographical coordinate system, and can get the trajectory curve of three axis x, y, z in geographic coordinate system after two integral operation for acceleration signal. The curve of x, y, z respectively represents projection parameters of rail lines in the vertical plane and horizontal plane and vertical plane, further combined with results of the cross section measurement system, ultimately get all the irregularity parameters we need [13] [14] . Through comparing the different results to acquire the deviation, the deformation can be calculated quantitatively, so that the workers can repair the serious abrasion timely. Moreover, during the actual measurement, what’s mainly concerned is the rail deformation of vertical and level plane, meaning the irregularity value of height and direction.
3. Empirical Mode Decomposition Algorithm
The basic method of empirical mode decomposition: Through continuous screening, the complex signal is decomposed into several intrinsic mode functions IMF component which are arranged from high to low frequency and the residual term, as shown in Equation (1), the concrete process can be referred to [15] .
 (1)
(1)
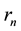 is residue component, representing average trend of the signal. And each IMF component
is residue component, representing average trend of the signal. And each IMF component ,
, 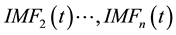 respectively contains different frequency signal components from high to low.
respectively contains different frequency signal components from high to low.
After decomposition, each intrinsic mode function (IMF) must be met two conditions following: 1) Through- out the time sequence, the number of passing zero is equal to the number of the pole or at best, a difference; 2) At any point, the mean value composed of local maximum value upper envelope and lower local minima enve- lope must be zero.
Figure 1. The image of motion trajectory.
After EMD decomposition we can get finite IMF: Among them, the big order corresponding to the low frequency component signals, is generally thought that little impact noise in the low frequency components; Small order corresponds to the high frequency component signal, often assume that contains a sharp part of the signal and noise [16] [17] . The main idea of using EMD method to deal with the noise is that main energy of most polluted signals is concentrated in low frequency band, the farther the high frequencies, it contains the less energy, so we can reconstruct signal partly by using several IMF in low frequency, namely:
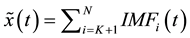 (2)
(2)
4. An EMD De-Noising Method Based on the Statistical Characteristic
4.1. Random Noise Power Statistical Properties
For the length of N discrete signal , the power calculation formula is:
, the power calculation formula is:
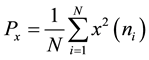 (3)
(3)
If keep the amplitude of original signal x (n) each element constant, to disrupt its location in order to get x’ (n), x (n) and x’ (n) can be determined power equal, namely, 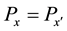 , the signal power stays the same after a random sequence.
, the signal power stays the same after a random sequence.
The following research is the changing rule of the noise power through random noise 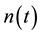 after the “random sort-accumulative-average”. Stochastic scheduling random noise
after the “random sort-accumulative-average”. Stochastic scheduling random noise  which sampling points is 2048 , totally 25 times repeated, after the i time random sort we can get the new noise
which sampling points is 2048 , totally 25 times repeated, after the i time random sort we can get the new noise , superimpose
, superimpose 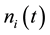 and the noise
and the noise 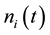 which is get from random sequence of i-1 before, can obtain a new noise component:
which is get from random sequence of i-1 before, can obtain a new noise component:
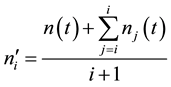 (4)
(4)
Computing the power of 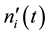 by Equation (3), then we can get a power?sort frequency curve, as shown in Figure 2. In Figure 2, the power
by Equation (3), then we can get a power?sort frequency curve, as shown in Figure 2. In Figure 2, the power 


Inspired by the above experiments, we let the imf1, imf2, imf3 component which is obtained after the EMD decomposition of the random noise 
Experimental results show that the first IMF component of random noise after EMD decomposition remains the approximate random features, for the first IMF component namely the imf1, in accordance with the “random sort-average accumulative” the new noise power decreases with the increase of number of random sequence.
Figure 2. Noise power-sort frequency curve.


Figure 3. Noise IMF component power-sort frequency curve.
4.2. The Statistical Feature of Random Noise Autocorrelation Function
The autocorrelation function of random signal is an average measure of the signal time domain features, reflecting the signal related degree at two different times t1, t2. Random signal 

The autocorrelation function of random noise 


where
The Figure 4 and Figure 5 show that although the normalized autocorrelation function of random noise 



4.3. The EMD De-Noising Algorithm Based on Noise Statistical Properties
According to the statistical characteristics analysis of random noise power, autocorrelation function [18] , put forward “the EMD de-noising algorithm based on noise statistical characteristics” and use “sort-accumulation- average-refactoring” order to suppress the noise. Specific steps are as follows:


Figure 4. Noise and normalized autocorrelation function.


Figure 5. Signal x (t) and normalized autocorrelation function.
Step 1: the EMD decomposition on noise signal
Step 2: remember


Step 3: stochastic scheduling 


Step 4: repeat Step 3 R times, calculate the average of accumulation to get a new noise dominant mode 
Step 5: get a new noise signal 


Step 6: 

Step 7: EMD decomposition on 
Step 8: global threshold selection method on the noise dominant mode component 
where 




Step 9: refactoring on 


5. Experimental Verification
5.1. Analog Signal
Using the method to deal with the noise of 




SNR of 







Continue to the EMD decomposition on













Figure 6. Noisy signals.


Figure 7. De-nosing results of test signals.

Figure 8. Each imf component of normalized autocorrelation function of 

Through the simulation experiments analysis: under the condition of low signal noise ratio (SNR), the EMD de-noising algorithm based on random noise statistical characteristics still can obtain good de-noising effect.
5.2. The Experiment Results Analysis
Experiment system uses XW-IMU5250 tiny mechanical inertial device of Beijing StarNeto Technology Development Co., Ltd. In the experiments for loading of the inertial measurement unit testing the car through an analog line segments, and then collect the inertial measurement unit acceleration along x, y, z axis among the car movement. First of all, using the average filtering method to eliminate the acceleration signal contained in the direct current; this method is applied to the actual inertial unit signal noise processing then. The waveform and spectrum diagram of de-noising before and after as shown in Figures 10-12.
Integral operation on x, y, z axis acceleration signal after de-noising, and through the attitude matrix transforms the movement information of vehicle coordinates to geographic coordinates, and get the car’s trajectory, the experimental results and the actual test vehicle by rail sections as shown in Figure 13, error range within ±0.5 mm.


Figure 9. De-nosing result of the proposed method.


Figure 10. The waveform and spectrum diagram of de-noising before and after of x axis acceleration signal.
6. Conclusion
In this paper, by using the random noise power, autocorrelation function statistical characteristics, a kind of suitable for low SNR signal de-noising method is put forward. The method can get the first component of the IMF after EMD decomposition on noise signal, in accordance with the “random sort-accumulation-average- reconstruction” order. We can get a reconstruction signal whose noise power is significantly weaken and signal power constant firstly, and then do EMD decomposition again for the reconstructed signal, and determine the cut-off point of signal-to-noise dominant mode by using signal autocorrelation function characteristics, realize the final de-noising signal reconstruction. Test results show that in low signal noise ratio (SNR) the method for de-noising effect is obvious. At the same time, good performance of inertial measurement unit in the treatment of orbital state detection signal provides a new thought for the future of inertial measurement unit signal processing.
Acknowledgements
The project is jointly supported by National Natural Science Foundation of China (Grant No. 51405287), the


Figure 11. The waveform and spectrum diagram of de-noising before and after of y axis acceleration signal.


Figure 12. The waveform and spectrum diagram of de-noising before and after of z axis acceleration signal.

Figure 13. Experimental platform orbit and space displacement curve after two integrals.
Shanghai Tertiary Education Specialized Fund for Planning to Support Young Teacher's Trainings (ZZGJD12007), the Natural Science Foundation of Shanghai (12ZR1412300), the Science and Technology Commission of Shanghai Municipality Key Support Project (13510501300), and the Shanghai Graduate Education Innovation Project in Layout and Construction Project (13sc002).
References
- Lu, Z.X., Su, Y.C. and Li, H. (2007) Super Track Long-Wave Irregularity Detection System Design. China Measurement &Testing Technology, 33, 16-18.
- Zheng, S.B., Lin, J.H. and Lin, G.B. (2007) Maglev Track Long-Wave Irregularity Detection Based on Inertia Method and Its Implementation. Journal of Electronic Measurement and Instrument, 21, 61-65.
- Chen, D.S. and Tian, X.Y. (2008) China’s High-Speed Rail Track Detection Technology Development. Railway Engineering, 12, 82-86.
- Weng, S.D. (1990) GJ-3 Track Detection System Development and Application. China Railway Science, 11, 54-64.
- Xu, G.Y., Cui, W. and Jiang, Y. (2000) GJ-4 Track Inspection Car and Its Effect on Transportation Safety. China Railway, 9, 51-52.
- Zhao, G., Liu, W.Z. and Chen, D.S. (2004) GJ-5 Track Inspection Car Independent Research and Development of the Software. Railway Engineering, 12, 45-46.
- Huang, N.E., Shen, Z., Long, S.R., et al. (1998) The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proceedings of the Royal Society, 454, 56-78.
- Boudraa, A.-O. and Cexus, J.-C. (2007) EMD-Based Signal Filtering. IEEE Transactions on Instrumentation and Measurement, 56, 2196-2202. http://dx.doi.org/10.1109/TIM.2007.907967
- Du, H.T., Gao, L.K. and Fan, G.P. (1997) The Application of Digital Filtering Technology in Orbit. China Railway Science, 18, 79-90.
- Du, H.T. (2000) Long Wavelength Track Irregularity Detection Method of Digital Filter. China Railway Science, 21, 58-64.
- Zhu, W.F., Chai, X.D. and Zheng, S.B. (2012) Based on the Track Long-Wave Irregularity of Strapdown Inertial System Test. Urban Mass Transit, 11, 87-90.
- Yang, Y.J., Huang, D.M. and Zhang, T.S. (2001) A Suitable for Engineering Practical Strapdown Attitude Algorithm. Journal of Chinese Inertial Technology, 9, 12-15.
- Zhang, Y., Ma, R.G. and Ding, H. (2007) The Laser Pavement Roughness Detection System Based on Inertial Reference Study. Computer and Communications, 25, 13-15.
- Mo, W.Q., Jiang, D.S. and Hu, W.B. (2004) Engineering Structure Based on Optic Fiber Gyro Strapdown Three-Dimensional Deformation Measurement Method. Optics & Optoelectronic Technology, 2, 15-17.
- Huang, N.E.,Wu, M.L., Long, S.R., et al. (1998) The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proceedings of the Royal Society, 454, 903-995. http://dx.doi.org/10.1098/rspa.1998.0193
- Jiang, L. and Li, C.Y. (2005) Based on Empirical Mode Decomposition of the Wavelet Threshold Denoising Method Research. Signal Processing, 6, 659-662.
- Zhao, W.W. and Zeng X.W. (2008) A New Method of EMD De-Noising. Electronic Science and Technology, 5, 30- 32.
- Wu, N.H. and Huang, N.E. (2004) A Study of the Characteristics of White Noise Using the Empirical Mode Decomposition Method. Proceedings of the Royal Society A, 460, 1597-1611. http://dx.doi.org/10.1098/rspa.2003.1221






